幾何畫板與高中數學教學有效整合策略

陳漢陽

摘? ?要：在新時代教育改革的背景下，多媒體技術被廣泛運用于高中數學教學之中，而如何融合多媒體技術與幾何畫板，實現對高中數學教學資源的有效整合，對于推動高中數學教學走向更高學術水平具有重要意義。從教學實踐出發，分析了現代教學在信息技術條件下幾何畫板與高中數學教學有效整合的策略。

關鍵詞：幾何畫板;高中數學;有效整合

引言：在新時代教育改革背景下，如何高效運用信息技術提升教學水準，是值得廣大教師深思的課題。以學科課程特點為基礎，推動信息技術與學科教育的深度融合，從而促使教學內容呈現出更加生動靈活的表現方式，則是教師值得關注的要點。這使得信息技術成為了學校教育教學的基本要素之一，也是推動教學水平提升的必要教學工具。

1? 從全局高度認識信息技術與數學教育

在高中數學教學實踐中，實現信息技術與數學課堂教學的有機整合，教師首先要從教學內容安排出發，合理利用信息技術，使課堂教學表達更加直觀生動，將數學課堂教學中含有學科特點的數學知識呈現方式變得更加形象多樣。這對于學生認識數學概念的形成與發展過程具有重要意義，學生在信息技術的支持下形成一定的數學思維，改變數學課堂教學的整體格局。從全局角度出發，充分認識信息技術與數學教學整合實踐的要點。教師不僅應當將信息技術作為教學的輔助工具，也要探索信息技術與數學課堂教學之間更多的融合點，從而實現更加高質量的教學整合。具體來看，為了促使幾何畫板、信息技術與數學課堂教學之間實現有機融合，以學生的實際學習情況為基礎，探索不同的教學整合方式。數學教師可采取以下幾種教學形式，一是將幾何畫板作為數學課堂演示工具，這種形式充分發揮了計算機軟件的演示功能，將學生難以理解的數學概念進行直觀展示。例如高中數學中的正方體截面、三角函數圖像等問題，教師都可以利用幾何畫板，從本質上揭示數學概念的特征，幫助學生形成較強的數學思維。在習題課與復習課教學時，可以利用幾何畫板畫出圖像，直觀理解題意，從而提高學生分析問題解決問題的能力，例如：

（2021全國高考試題21）在平面直角坐標系xOy中，已知點F1=（-，0），F2=（，0），│MF1│-│MF2│=2，點M的軌跡為C.（1）求C的方程;（2）設點T在直線x=上，過T的兩條直線分別交C于A，B兩點和P，Q兩點，且│TA│·│TB│=│TP│·│TQ│，求直線AB的斜率與直線PQ的斜率之和. 解析：（1）軌跡C的方程為x-=1（x≥1）;（2）設點T（，t），若過點T的直線的斜率不存在，此時該直線與曲線C無公共點，不妨直線AB的方程為y-t=k1（x-），即y=k1x+t-k1，聯立y=k1x+t-

k1

16x2-16y2=16，消去y并整理可得（k-16）x+k（2t-k）x+（t-k）+16=0，設點A（x1，y1）、B（x2，y2），則x1>且x2>.由韋達定理可得x1+x2=，x1x2=，所以，│TA│·│TB│=（1+k）·│x1-│·│x2-│=（1+k）·（x1x2-）=，設直線PQ的斜率為k2，同理可得│TP│·│TQ│=，因為│TA│·│TB│=│TP│·│TQ│，即=，整理可得k=k，即（k1-k2）（k1+k2）=0，顯然k1-k2≠0，故k1+k2=0。因此，直線AB與直線PQ的斜率之和為0。在第一小題中，利用圖像，可以明確限制范圍，在第二小題中，利用圖像，可以明確解題思路與方法。二是通過課件制作，在課堂上向學生進行演示，并號召學生參與到操作過程中來，讓學生更加主動積極地開展數學課堂活動。三是讓學生進行自主研究，并以幾何畫板作為輔助工具，讓學生通過獨立操作電腦軟件，研究相關的復雜數學問題，這種教學形式能夠充分發揮學生的主觀能動性，學生在操作軟件過程中，也將形成一定的解決問題能力和創新意識。基于以上三種教學形式的有機整合，教師能夠充分發揮幾何畫板的輔助作用，并幫助學生弄清數學問題的原理。在當前教育形勢下，教師要進一步探索幾何畫板與數學教學的融合要點，以數學學科特點為基礎，讓學生思考數學知識的發生和形成過程。

2? 幾何畫板與數學課堂教學有機整合的必要原則

2.1? 尊重幾何畫板的工具性原則

為了促使幾何畫板在數學課堂教學過程中更大程度地影響學生的學習過程，教師應當盡量減少對幾何畫板自身的過度關注，而是要以學生的認知水平為基礎，尊重學生的思維能力和幾何畫板的工具性。在數學課堂教學過程中，教師要將幾何畫板作為服務于教學的基本工具，以一種更加自然和開放的態度對待幾何畫板，將幾何畫板變為幫助學生獲取數學信息、探索數學問題、解決復雜問題的輔助工具。教師要轉變學生對幾何畫板這種學習工具的認知，讓學生在操作幾何畫板時更加順手和自然[ 1 ]。

2.2? 堅持教學有效性原則

在高中數學課堂教學中充分利用幾何畫板，教師要實現對教學難點的充分突破，幫助學生建立起更加高質高效的學習方式。對于高中數學而言，在應對一些相對復雜的數學問題時，如果教師僅僅利用傳統的教學手段，難以使學生清楚理解這些數學原理，而如果能夠充分利用幾何畫板，這些教學難點將會得到充分化解。例如在高中數學課堂教學中，教師可以利用幾何畫板詳細解釋幾何圖形的平移和旋轉問題.例如：（2018全國高考試題19）設橢圓C：+y=1的右焦點為F，過F的直線l與C交于A，B兩點，點M的坐標為（2，0）. （1）當l與x軸垂直時，求直線AM的方程;（2）設O為坐標原點，證明：∠OMA=∠OMB。解析：（1）由已知得F（1，0），l的方程為x=1.由已知可得，點A的坐標為（1，）或（1，-）.所以AM的方程為y=-x+或y=x-.（2）當l與x軸重合時，∠OMA=∠OMB=0°。當l與x軸垂直時，OM為AB的垂直平分線，所以∠OMA=∠OMB。當l與x軸不重合也不垂直時，設l的方程為，y=k（x-1）（x≠0），A（x1，y1），B（x2，y2），則x1<，x2<，直線MA，MB的斜率之和為kMA+kMB=+。由y1=kx1-k，y2=kx2-k得。kMA+kMB=。將y=k（x-1）代入+y=1得（2k2+1）x-4k2x+2k2-2=0。所以，x1+x2=，x1x2=。則2kx1x2-3k（x1+x2）+4k==0。從而kMA+kMB=0，故MA，MB的傾斜角互補，所以∠OMA=∠OMB。綜上，在第一小題中，利用圖像，可以明確本題有兩解，在第二小題中，利用圖像，可以明確把證明角相等轉化為斜率相加等于0。與此同時，教師要進一步關注學生的學習效率，幫助學生構建起更加高效的學習方式，教師要促使學生在學習過程中更加積極主動，通過不斷地探索和研究認識數學原理。而基于這種學習方式，學生能夠形成更加端正的學習態度，這對于學生的長期成長同樣具有積極意義。總體來看，在多媒體環境下利用幾何畫板，教師一定要尊重教學的有效性原則，從根本上解決學生關注的學習問題，這樣才能充分發揮幾何畫板的輔助作用。

3? 多媒體條件下幾何畫板與數學教學整合策略

3.1? 幾何畫板與數學教學整合的基本形式

在多媒體技術條件下，數學教師充分利用幾何畫板主要有以下三種基本的體現形式，一是利用幾何畫板進行驗證性演示，教師可以以課本教材的教學內容安排為基礎，設計特定的幾何畫板課件，并借助幾何畫板的動態演示，從而驗證一些數學概念。二是構建性整合，教師可以以學生自身的知識水平和認知水平為基礎，幫助學生主動構建一些陌生的數學概念。例如在解析幾何的學習過程中，教師可以引導學生利用幾何畫板，對曲線的軌跡進行探索研究，之后，教師也可以引導學生通過數學方法解出相關方程。三是探究性實驗，教師可以帶領學生利用幾何畫板進行探究性學習，在這種應用過程中，學生將會深刻認識某一數學的產生和發展過程。

3.2? 進行針對性教學設計，實現有效教學整合

教師在充分利用幾何畫板的過程中，必須進行有針對性的教學設計，并以特定的教學目標和學生的基本認知水平為基礎，對教學整合內容進行全方位設計。教師需要了解學生的學習需求，并通過設計教學目標和教學手段，幫助學生了解數學知識、應用數學知識、綜合評價數學知識。在當前高中數學課堂教學中，教師在應用幾何畫板時，不僅要使幾何畫板成為完成教學任務的輔助工具，更要讓幾何畫板成為學生發展認知水平的基礎工具。例如在學習函數y=Asin（ωx+φ）的圖像相關知識時，教師可以設計幾何畫板課件，讓學生利用幾何畫板，對該三角函數進行作圖，并以此為手段，探索A，ω，φ等系數對函數整體圖像的影響程度。通過觀察電腦圖形的變化過程，教師可以引導學生進行討論，從而幫助學生深刻認識數學知識原理，形成數學知識體系，實現數學應用能力的有效提升[ 2 ]。

3.3? 發展教學創意，保障教學整合

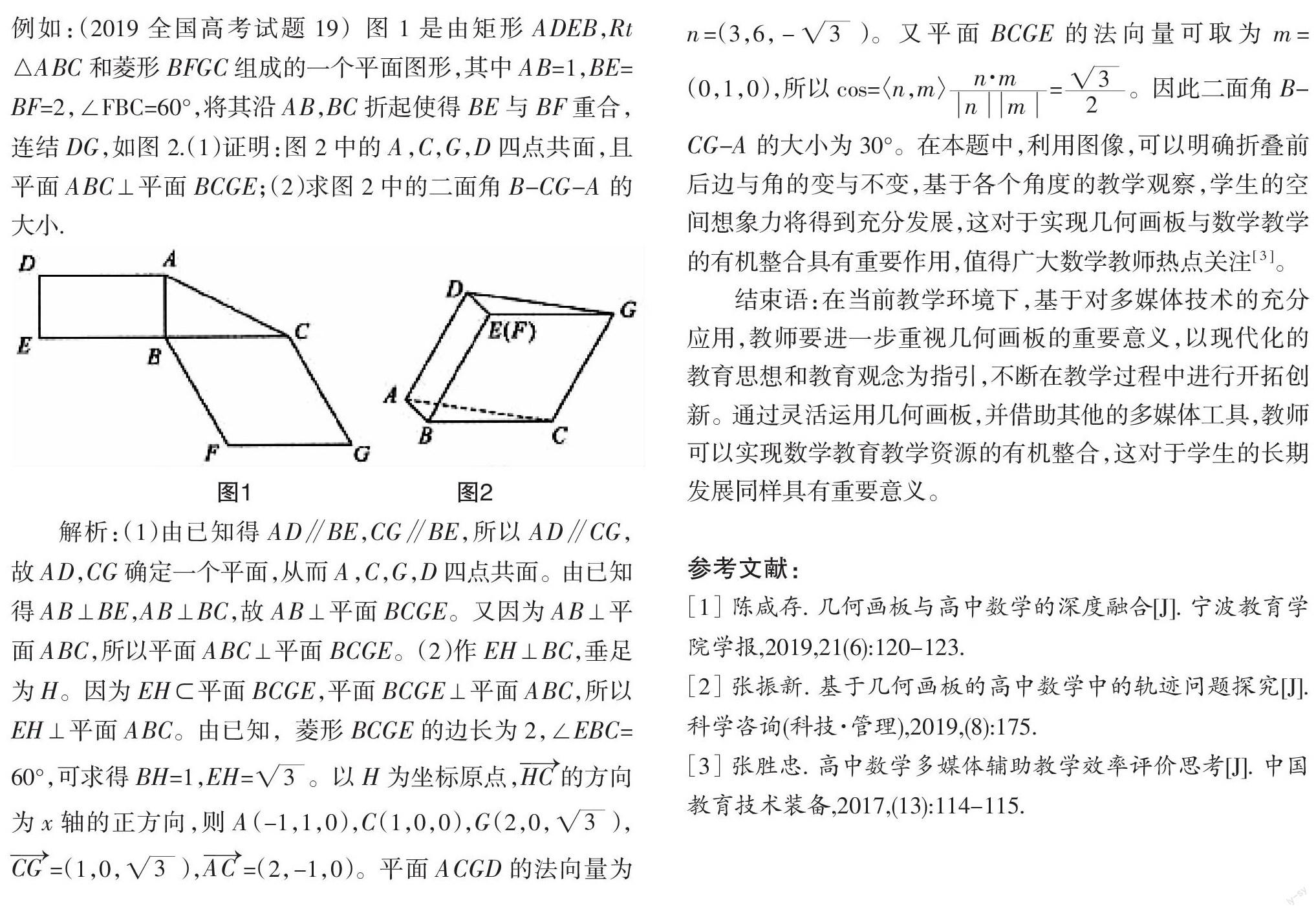
為了更大程度發揮幾何畫板在高中數學課堂教學中的積極作用，教師要針對個人的教學方法進行不斷的開拓創新，以更加積極的教學創意，改變數學教學總體格局。例如，教師可以在教學設計、教學內容、教學方法和教學手段上進行全面創新，以創造性的手段，不斷解決數學教學過程中出現的不同層次的問題。一方面，教師可以通過幾何畫板，對一些較為復雜的數學公式和數學定理進行展示，幫助學生領悟數學知識的本質。另一方面，教師也要尊重數學教材和高考評價體系，利用數學知識的拓展與探究活動，進一步激發學生進行研究性學習的積極性。教師要以教材內容為基礎，選取教材中相對典型的素材，利用幾何畫板體現數學概念和結論的發展過程，幫助學生感受數學的自然性和邏輯性，讓學生體會數學的力量，進一步啟發學生的數學思維。例如，在講解立體幾何的空間構圖特點時，教師可以充分利用幾何畫板，對立體圖形的動態演變過程進行直觀展示。教師可以簡單拖動立體圖形中的某些點，從而實現對整個圖形的變化。例如：（2019全國高考試題19）圖1是由矩形ADEB，Rt△ABC和菱形BFGC組成的一個平面圖形，其中AB=1，BE=BF=2，∠FBC=60°，將其沿AB，BC折起使得BE與BF重合，連結DG，如圖2.（1）證明：圖2中的A，C，G，D四點共面，且平面ABC⊥平面BCGE;（2）求圖2中的二面角B-CG-A的大小.

解析：（1）由已知得AD∥BE，CG∥BE，所以AD∥CG，故AD，CG確定一個平面，從而A，C，G，D四點共面。由已知得AB⊥BE，AB⊥BC，故AB⊥平面BCGE。又因為AB⊥平面ABC，所以平面ABC⊥平面BCGE。（2）作EH⊥BC，垂足為H。因為EH?平面BCGE，平面BCGE⊥平面ABC，所以EH⊥平面ABC。由已知，菱形BCGE的邊長為2，∠EBC=60°，可求得BH=1，EH=。以H為坐標原點，的方向為x軸的正方向，則A（-1，1，0），C（1，0，0），G（2，0，），=（1，0，），=（2，-1，0）。平面ACGD的法向量為n=（3，6，-）。又平面BCGE的法向量可取為m=（0，1，0），所以cos=〈n，m〉=。因此二面角B-CG-A的大小為30°。在本題中，利用圖像，可以明確折疊前后邊與角的變與不變，基于各個角度的教學觀察，學生的空間想象力將得到充分發展，這對于實現幾何畫板與數學教學的有機整合具有重要作用，值得廣大數學教師熱點關注[ 3 ]。

結束語：在當前教學環境下，基于對多媒體技術的充分應用，教師要進一步重視幾何畫板的重要意義，以現代化的教育思想和教育觀念為指引，不斷在教學過程中進行開拓創新。通過靈活運用幾何畫板，并借助其他的多媒體工具，教師可以實現數學教育教學資源的有機整合，這對于學生的長期發展同樣具有重要意義。

參考文獻：

[1] 陳咸存. 幾何畫板與高中數學的深度融合[J]. 寧波教育學院學報，2019，21（6）：120-123.

[2] 張振新. 基于幾何畫板的高中數學中的軌跡問題探究[J]. 科學咨詢（科技·管理），2019，（8）：175.

[3] 張勝忠. 高中數學多媒體輔助教學效率評價思考[J]. 中國教育技術裝備，2017，（13）：114-115.