基于ARMA模型的鄭州市氣溫衍生品定價研究

王福寧

一、引言

天氣衍生品是建立在溫度、濕度、降水、風等天氣變量上的金融合約。自1999年第一份溫度期貨合約在芝加哥商品交易所（CME）交易以來，天氣衍生品已成為管理天氣風險的最重要的金融工具。

氣溫衍生品是天氣衍生品市場中最常見的一種類型，有一些文獻[1，3]涉及氣溫建模，其中Alaton[1]引入了隨月份變化波動率的Ornstein-Uhlenbeck （O-U）過程來模擬氣溫演化。Cao 和Wei[3]利用均值回歸模型模擬氣溫，建立了基于氣溫的動態評估模型。由于天氣衍生品市場是不完備的，所以經典的金融衍生品定價方法，如Black-Scholes公式并不適用。 因此，研究者們從不同角度提出了多種方法，如邊際效用法[4]、指數建模[5]、均衡定價[6]、ARMA時間序列模型法[7-9]等。 Li Peng，Xiaoping Lu，Song-Ping Zhu[10]基于偏微分方程方法，利用效用無差異估值中提取的市場風險價格對天氣衍生品進行定價。Li Peng[11]對兩個典型過程的天氣衍生品進行了定價：Ornstein–Uhlenbeck過程和帶跳躍擴散的Ornstein–Uhlenbeck過程，并用單側Crank–Nicolson格式，分別求解這兩個過程對應的偏微分方程和積分微分方程。

本文擬在已有研究的基礎上，采用ARMA時間序列模型對鄭州市氣溫變化過程進行建模，并利用該模型進行氣溫預測，最后檢驗模型的準確性。

二、 數據與研究方法

（一）數據來源與預處理

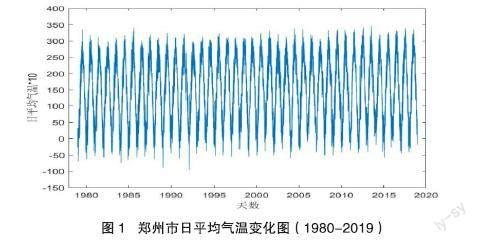
鄭州是河南省的省會城市，是中國中部重要的交通樞紐和農業城市。從中國氣象科學數據共享服務網收集了1980-2020年間的日平均氣溫數據，為了消除閏年的影響，剔除了所有閏年2月29日的日平均氣溫。因此，共有14965個觀測值，沒有缺失數據。利用鄭州市40年（1980-2019年）的日平均氣溫數據來構建氣溫預測模型，并用預測模型預測鄭州市2020年的日平均氣溫。

經過Matlab R2019a 軟件處理，得到了40年的日平均氣溫的折線圖，如圖1所示。

（二）模型的建立

根據前文分析得出，鄭州市日平均氣溫數據的變化過程具有很強的季節性變化，可以用一些正弦函數來模擬季節相關性，函數形式如下：

式中，t表示時間，以天為單位，為相位角，日平均氣溫的季節性變化呈現出以一年為單位的周期性，為了數據統一，刪除閏年2月29日的氣溫數據，應取。因受到全球的溫室效應，每年的氣溫以微弱的趨勢增長，可以合理的假設這種微弱的變化是線性的，用Bt表示。因此，鄭州市日平均氣溫變化過程可寫為如下形式：

其中Tt為時間t的日平均氣溫，A、B、C以及是由歷史日平均氣溫數據擬合的參數，Xt為去除趨勢和季節性后的隨機變量。

為便于參數估計，將（2）式作如下等式變換：

整理可得：

因為和是常數，所以可將（4）式看成是一個線性方程：

即：

三、模型的參數估計與結果分析

（一）ARMA模型的估計

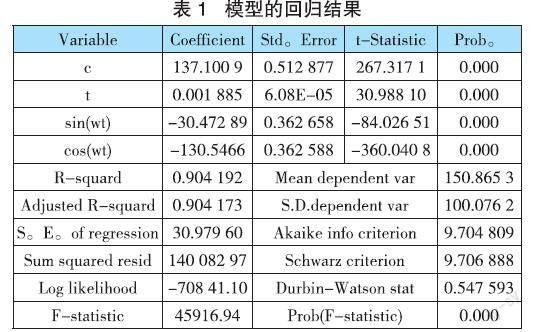
用Eviews 10軟件對公式（5）進行參數估計，得到結果如表1所示。

由表1可知，各項變量系數都顯著，但D-W值僅為0.547593，說明模型存在序列正相關性，需要對其進行修正。首先對隨機變量進行單位根檢驗，結果見表2。由表2可知，ADF檢驗的統計量為-43.61932，明顯小于在1%、5%、10%的顯著性水平下的臨界值，說明隨機變量沒有單位根，且序列平穩。其次，通過對隨機變量繪制出自相關系數圖和偏自相關系數圖后，可以判斷出它是一個平滑的非白噪聲序列。因此，需要引入ARMA模型進行修正隨機變量，發現引入ARMA（2，2）后，各項系數顯著，D-W值為2.001 518，十分接近于2，說明模型不存在序列相關性，模型擬合的結果好，具體結果見表3。

（二）預測結果

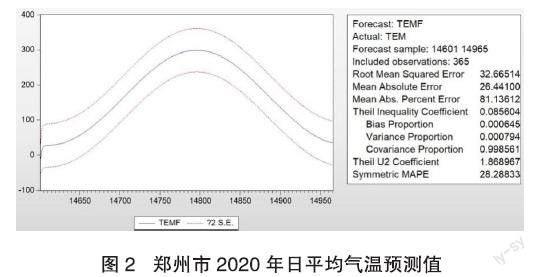
根據上述分析所得的時間序列ARMA模型，運用Eviews10軟件對鄭州市2020年的日平均氣溫進行預測，發現所構建的模型比較好，見圖2。

本文通過計算偏差比率、方差比率和協方差比率進一步驗證了模型的準確性，其三個比率值計算結果分別為0.000645，0.000794，0.998561。從這三個值中可看出偏差比率和方差比率的值較小，協方差比率值較大，且三個值和1，說明該模型預測較好。

四、 基于蒙特卡洛方法對氣溫衍生品定價

選取累積制冷指數（cooling degree days，CDDs）為研究對象，探討氣溫的期貨定價問題。 CDDs的表達式為：

其中是基準溫度，基準溫度一般是65華氏度或18 攝氏度，根據我國國情，選擇。Ti是第i天的日平均氣溫。

假設期權的合約期限在T1和T2之間，且T2是合約的到期日，r為無風險利率，C為名義價值，S（T）為到期時標的資產的實際價格，F（t）為遠期合約在時間t時的價值，原理上，當無風險利率為常數，期貨合約和遠期合約有相同的到期日和交割日時，其期貨合約的價格等于遠期合約的價格。即

這里的E為風險中性測度下的期望，我們假定風險市場價格為0。

選擇CDDs期貨合約為例，預期合約的終值為預期的CDDs值，即CDDs在時刻t的期貨價值為：

根據上式（11）可知，是已知的，只需用蒙特卡洛方法計算。

選擇2020.8.1-2020.8.31為合約期限，合約的名義價值C=100，即每點CDDs指數為100元，采用蒙特卡洛方法，計算出這一時期內CDDs值。當經過100000次模擬后，發現CDDs模擬值趨于穩定，達到仿真要求。

五、展望

我國的天氣特征具有復雜性且受到多種因素的影響，天氣的變化與各個行業以及我們的生活息息相關，如2021年河南7.20強降雨事件，給各個行業的發展和市民的生活帶來了諸多影響，農業生產損失更是高達上億元。因此開發出適應我國的天氣衍生品用于應對天氣風險具有一定的現實意義，而我國目前的天氣衍生產品市場亟待完善，需要來自金融市場、法律甚至是媒體等多方共同努力來促進天氣衍生品市場的蓬勃發展。

參考文獻：

[1] Alaton， Djehiche and Stillberger.On Modelling and Pricing WeatherDerivatives.Applied Mathematical Finance，2002，9：1-20.

[2] Bhowan A.Temperature derivatives School of Computational and Applied Mathematics，University of Wiwatersrand.2003.

[3] Cao M.and Wei J.Weather derivatives valuation and market price of weather risk. Future Markets， 2005，24（11）：1065-1089.

[4]M. Davis.Pricing weather derivatives by marginal value[J]. Quantitative Finance， 2001， 1（3）： 305-308.

[5] Gregor Dorfleitner，Maximilian Wimmer. The pricing of temperature futures at the Chicago Mercantile Exchange[J].Journal of Banking and Finance， 2009，34（6）：1360-1370.

[6] Yongheon Lee， Shmuel S. Oren. An equilibrium pricing model for weather derivatives in a multi-commodity setting[J]. Energy Economics， 2009， 31（5）：702-713.

[7]郭建國，牛珊.基于ARMA模型的氣溫衍生品定價研究[J].商業經濟，2015（10）：40-41+69.

[8]曾小艷，陶建平.基于ARMA模型的氣溫衍生品定價研究：以武漢市為例[J].區域金融研究，2014（07）：12-17.

[9] 李嫣然.天氣金融衍生品定價研究—基于ARMA的時間序列模型[J].保險職業學院學報，2017，31（04）：28-33.

[10] Li Peng， Xiaoping Lu， Song-Ping Zhu. Pricing weather derivatives with the market price of risk extracted from the utility indifference valuation， Computers and Mathematics with Applications， 2020，79： 3394C3409.

[11] Li Peng. The valuation of weather derivatives using one sided Crank-Nicolson schemes. Computational Economics，2020.

作者單位：華北水利水電大學數學與統計學院