初中數學中關于“圓”的解題策略

阿班

【摘要】在初中數學知識學習的過程中，“圓”的解題特征具有較強的靈活性及多解性，致使學生在解題過程中容易出現錯誤.因此，為避免這一現象，教師可以從圓的基礎定理入手，啟發學生對圓的引申知識進行創新、探究和思考，激發學生對關于“圓”知識內容的進一步學習.同時，教師還應引導學生遵循數學知識的一般學習規律和解題習慣學習“圓”的內容，讓學生學會對“圓”知識內容的活學活用，提高學生的解題能力，本文就此展開論述.

【關鍵詞】初中數學;圓;解題策略

1 前言

作為初中數學中的一項主要學習內容，“圓”的知識點學習內容能夠影響到學生未來的數學學習，是一種基礎性較強的知識內容.為使學生對“圓”知識點的內容高效理解，教師應結合考試題型對學生開展“圓”知識內容的教學引導，使學生能夠理解圓的對稱性、圓周角及圓的輔助線知識內容，提高學生的解題能力，使枯燥內容能夠變得形象易懂，以此提高學生的數學知識核心素養.

2 以圓的基本定理歸納題型

傳統層面的一題一分析學習模式，其教學效率不高，且難以提高學生的解題能力.所以，教師可以結合圓的基本定理，引導學生分析圓的知識內容，以此提高學生的數學問題思辨素養.

圓周角的定理是指：在圓周的頂點上，且兩邊為圓的兩條弦的角，即圓上有圓周角的頂點，等弧或同弧對應的圓周角，都與這條弧對應的圓心角的一半相等.在關于圓周角的計算題、證明題解題方面，若從圓周角及圓心角方面開展思考，都可以便捷地找到解題思路，進而縮短學習時間.

在開展解題的過程中，以“圓的認識與圓的對稱性”為例，本知識點的學習基本內容為，理解圓的對稱性，圓是由無數條對稱軸組成的，每一條經過圓心的直線都是其對稱軸.還應學習垂徑定理內容，與弦的直徑平分且垂直，且弦對應的兩條弧平分.

在對此問題進行解決的過程中，教師應啟發學生先思考圓周角定理，并要求學生掌握圓心角、弦、弧之間的關系，掌握垂徑定理并以定理進展證明，對圓的旋轉不變性進行理解.

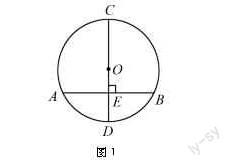
例如 在⊙O中，AB是弦，直徑為CD，假如AB⊥CD于E，那么AC=BC，AD=BD.（見圖1）

通過本案例推論垂徑定理，對于一條直線及一個圓而言，只要具備五條定理中的兩條，就能將其他三條定理推導出來，五條定理分別為：與弦垂直、過圓心、平分弦、平分弦所對的劣弧、平分弦所對優弧.結合教材層面的定義進行推論，平分弦（非直徑）的直徑與弦垂直，且將弦所對應的弧平分.同時，圓也是中心對稱圖形，圓心是其對稱中心，圓還具有旋轉不變性.

例1 在⊙O中，AB與⊙O相交于C、D，且BD=AC，那么，OB=OA嗎？說出理由.

在這道例題中，教師可以引導學生思考，過點O作AB⊥OE于E，所以DE=CE，又因為BD=AC，所以BE=AE，因此，OE是AB的中垂線，而根據圓的垂線定理可知，中垂線上的任意一點，到線段兩端的距離相等，所以OB=OA.

例2? 有兩個同心圓以O為圓心，大圓的弦AB與小圓相交于兩點C、D，求證，AC=BD.（見圖2）

證明 過O作AB⊥OE，結合垂徑定理進行分析，垂直于弦的直徑不僅能將弦平分，也能將這條弦所對應的兩條弧平分，則AB被OE平分，CD也被OE平分，因此，DE=CE、BE=AE.又因為BE-DE=BD、AE-CE=AC，所以BE-DE=AE-CE，即BD=AC.

例3 ⊙O的弦CD和直徑AB在E點相交，∠CEA=30°，EB=2cm，AE=6cm，求CD的長度.（見圖3）

在解決本題的過程中，需要明確此題是利用垂徑定理開展的計算問題，在求相關的半徑、弦長、弦心距等問題的過程中，通常都會對半徑和弦心距構成的直角三角形問題進行求解，而單純應用“相交弦”定理解決此題會存在一定的難度.

因此，應充分利用已知條件∠BED =30°，構造出一個以半弦、半徑、弦心距組成的直角三角形，在對直角三角形問題進行求解后，能夠求出未知量[2].

解析 過O作CD⊥OF于點F，將OF、CO連接，因為EB=2，AE=6，所以AB=8，所以OE=AE-OA=2，OC=OA=12AB=4，

又因為在Rt△OEF中，∠AEC=30°，所以OF=12OE=1.

又因為在Rt△COF中，OF=1，OC=4，所以CF=x= 15，又因為CD⊥OF，所以DF=CF，所以CD=2 15.

3 以圓周角開展題型練習

通過案例分析圓形的解題步驟，深入地幫助學生理解圓形問題，提高學生的解題能力.在相關圓的知識點學習過程中，應明確的是其中還包括圓周角計算題目，在實際進行解題的過程中，這類題目多以填空題、選擇題的形式出現.在解決此類問題的過程中，學生可以通過一定的解題技巧解決問題，盡量以最短的時間完成解題內容，以此提高解題效率.

在進行解題環節，學生可以結合題目中圓周角以及其所對應的圓心角、弦、弧進行解題，可以通過典型案例講解法，并通過讓學生完成大量練習的方式，增加對本知識內容的記憶.

教師可以啟發學生先分析例題，再開展練習，使學生能夠在教師指導的方法下做題，使學生的解題熟悉度得以增加.學生在掌握了基本學習方法后，教師應對學生進行深入引導，要求學生模擬教師的計算方法，并嘗試將題目的答案在練習紙上進行分析、演練.

例4 在⊙O上分別有點A、B、C，∠AOB=72°，則∠ACB等于（? ）

（A）36°. ?（B）18°. ?（C）54°. ?（D）28°.

解析 根據圓周角定理可以對這一問題進行解題，圓周角定理反映的是圓心角與圓周角的關系，指的是一條弧所對應的圓周角，與它所對應的圓心角的一半相等，且等弧或同弧對應的圓周角相等[3].根據圓周角定理進行確定，當∠AOB=72°的時候，∠ACB=36°，因此，這道填空題的答案為（A）（見圖4）

例5 若⊙O的直徑為AB，AC=AB，∠ABE=45°，AC在⊙O的E點上相交，BC在⊙O的D點上相交.需要對∠EBC的度數進行計算，以及對CD=BD進行求證.（見圖5）

本題考查的是等腰三角形三線合一定理、等腰直角三角形的性質和判定、圓周角定理等知識，解題的關鍵點是應對相對應角的度數問題進行解答.

解析 本題中圓的直徑為AB，由于∠AEB=90°，∠ABE=45°，AC=AB，進而∠ACB=∠ABC，而這些已知條件是求∠EBC的關鍵點.將AD連接，由于∠ADB=90°，AC=AB，根據等腰三角形三線合一定義可知CD=BD.

解問題1，將AD連接，因為⊙O的直徑為AB，所以AC⊥BE，BC⊥AD，因為∠ABE=45°，∠A=45°，又AB=AC，所以∠CAD=∠BAD=22.5°，所以∠CAD=∠EBC=22.5°.

解問題2，因為BC⊥AD，AC=AB，所以CD=BD.

例6 （見圖6）已知△ABC，以AB為直徑的⊙O分別交BC于E，交AC于D，連接ED，若EC=ED.

（1）求證：AB=AC;

（2）若AB=4，BC=23，求CD的長.

本題考查的是學生是否能夠以圓周角定理及勾股定理分析問題，以此提高學生的圓形知識應用能力.

解 將BD連接，因為AB為直徑，所以AC⊥BD，設CD=a，由于AB=AC=4，則AD=4-a，可以通過勾股定理分析此題，將半徑、弦心距、半弦三者在同一個直角三角形中進行分析，比如，Rt△CBD中，BD2=BC2-CD2=（23）2-a2，所以（23）2-a2=42-（4-a）2，整理可得，a=32，即CD=32.

4 以圓的輔助線開展題型交流

圓的知識涉及到的知識點較多，且關于圓的題目涵蓋基礎題、綜合題等.學生在學習基礎題目的過程中，大都能輕松地完成試題內容，但進入綜合題學習階段，學生的學習不足就會凸顯出來.為突破這一現象，教師可有計劃對對學生進行教學引導，圓類的知識點中涵蓋函數、直線與圓等知識，這類知識點問題復雜，需要輔助線進行輔助教學，但學生大都對輔助線類的知識存在學習難度.教師可以通過題型交流的方式，總結出輔助線的添加方式，以此提高學生的解題能力.

比如，在解決弦的問題過程中，通常需要作出圓心到弦的垂線段，這是一種輔助線即弦心距，主要是為了通過垂徑定理，獲得平分弦的條件，也是為了通過對直角三角形的構造，結合勾股定理的方式解題.

再比如，在解決同弧或等弧問題的環節，常連等弧對應的圓心角.在解決上述數學問題的過程中，可以通過輔助線的方式完成.

再比如，在學習已知弦中點時常連弦心距的過程中，也應通過輔助線的方式開展教學.

5 結語

綜上所述，雖然圓形是一筆形成的圖形，貌似很簡單，實則卻蘊含了豐富的內容.而圓也是一種最基本的平面圖形，關于圓的題目，教師可以引導學生通過學習圓的基本定理、圓周角及畫輔助線的方式啟發學生學習，這會簡化學習難度.同時，“圓”知識點的教學目的還在于提高學生的邏輯思維素養及數學知識的綜合運用能力，教師可以通過引導學生解題的方式，幫助學生對更多的關于圓的圖形問題進行練習，在完成習題的過程中，理解圓的定理，從而實現逐步提高數學綜合能力的目的.

參考文獻：

[1]張長新.九年級數學中關于“圓”的解題策略教學[J].科學咨詢（教育科研），2020（08）：279.

[2]藍奇靈.初中數學教學中幾何畫板的應用[J].科學咨詢（教育科研），2020（06）：273.