初中數學動點問題的教學策略研究

馮玲玉

【摘要】在初中數學的復習中，動點問題是重難點所在，同時也是中考的必考題型，而動點問題中的二次函數的應用為例，又是學校在初中數學復習中的主要難點，這就要求教師在平時教學中要采用合理的練習步驟和教學策略，以正確引導學生解題，進而發散學生的數學思維，從而提高思維能力，并改善教學方法.

【關鍵詞】二次函數動點問題;教學策略

初中數學課程開始涉及函數，函數問題都是初中數學學習的重點和難點，尤其是二次函數更是中考壓軸題當中的必考點，通常會以動點題的形式出現，而動點問題也是學生們學習數學的難點之一，根據學生們課堂的反饋以及做題情況來看，動點問題復雜而且難以理解.考察了學生對于基礎知識的掌握情況以及深入探究知識的能力.所以對于二次函數動點問題的教學策略研究至關重要，那么我們就以二次函數為例展開研究.

1 初中數學二次函數動點問題的簡述

二次函數動點問題被定義為：通過研究一個動點問題把函數的基本特性與幾何圖形有機組合，這就需要學習者對二次函數動點問題具有比較強的理解力，對學習者來說就具有一定挑戰性，此外，學習者一旦能了解二次函數動點問題，綜合運用理論知識的能力和解題的能力就會增強，因此研究問題也就會比較輕松.能夠利用掌握的函數基礎知識去解題，這不僅可以鞏固學習知識點，還可以提高學生思考和解決實際問題的能力，從而傳播學生的數學思想，教會學生將數與形、數學建模相結合，形成數學思維，解決實際問題[1].

2 解決數學動點問題的困難分析

2.1 學生在解決動點問題時的困難

初中數學動點問題涉及的知識具有很強的綜合性，解決問題的要求比較高，導致很多學生在解題時遇到困難，不知從何入手.那么困難點體現在哪些方面呢？總結以下的幾個方面：一是存在理解性困難.對于題目的關鍵信息和隱含條件，以及需要求的問題等內容很難理解，不能準確把握題中關鍵條件以及切入點，思路不清晰，題中的問題不能與所學知識聯系起來，導致理解困難.第二，有選擇性的困難.動點問題的求解方法具有很強的靈活性.許多學生不知道思考問題時應該選擇哪些數學公式、定理和解決問題的方法，進而解題思路不清晰.第三，無法找到變量關系.二次函數關于動點問題的描述相對較長，一些學生遇到偏長的題目會有抵觸心理，不會將文字信息轉化為數學信息，建模能力較弱，不會提煉關鍵條件，問題中變量、不變量與實際條件之間的聯系都不能發現，連函數關系也不能表示，使得難題不能準確地解決[2].

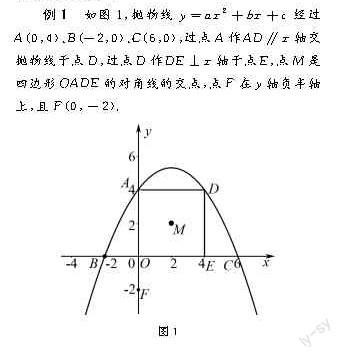
例1 如圖1，拋物線y=ax2+bx+c經過A（0，4）、B（-2，0）、C（6，0），過點A作AD∥x軸交拋物線于點D，過點D作DE⊥x軸于點E，點M是四邊形OADE的對角線的交點，點F在y軸負半軸上，且F（0，-2）.

（1）求拋物線所對應的函數關系式，并直接寫出四邊形OADE的形狀;

（2）當點P、Q從點C、F同時出發，點以1m/s的速度沿CB、FA方向運動，移動時間為t秒，在運動過程中，以P、Q、O、M四點為頂點的四邊形的面積為S，計算出S與t之間的函數關系式，并寫出自變量的取值范圍[3].

分析 （1）解題關鍵為將點代入解析式并求出二次函數關系式，再通過二次函數關系式性質判斷圖形，同時考察了四邊形的判定定理.（2）解題關鍵在于找出題中全等三角形并運用三角形面積來解題，進而求出S與t之間的函數關系式.但許多學生求出二次函數關系式以后不能進行綜合分析，不能將動點問題與全等三角形的判定有機結合，因而導致解題出現困難.

2.2 出現困難的原因分析

學生在解決動點問題時會出現困難，分析原因有以下兩方面：

2.2.1 教師方面的原因

其一是教師教學態度的影響.動點問題對于學生來說確實是難題，偏題，有些教師在遇到此類問題時，不能做到耐心、細致、反復地為學生講解;其二是教師教學方法的影響.部分教師在講解此類問題的方式較為單一和固化，講授課程機械化或者課堂枯燥乏味，不能將現代化的教學手段應用到教學當中，可以應用多媒體教學或者引入動態畫板到教學當中，直觀演示和講解相結合，缺乏探索精神.所以，這就無法豐富學生的數學思想和開闊學生的眼界，也造成了學生思想的固化和解決問題的障礙;三是老師不能掌握學生求解難點的因素，就不能因材施教.如果教師不能掌握不同學生求解難度的因素，就無法解決學生的問題.

2.2.2 學生方面的原因

動點問題由于題型的復雜性和綜合性強，對學生而言既是難題又是痛點，原因主要有以下三方面：首先，認識力不佳.初中階段學生的抽象思維能力還處在上升的發展階段，易受意志、心態、情感等非智力因素的影響以及對現有數學文化知識的限制，造成了學生對二次函數動點問題在具體解決方面的知識欠缺;其二，解題的思路并不清晰，思路也不夠敏捷，所見問題較少，也沒有解題的整體意識，面臨各種類型問題也找不到解題的突破口，導致困難增加，進而失去了對動點問題的解題興趣;其三，缺乏解題經驗.部分學生對解決動點問題缺乏興趣，解題的方法不夠多樣化，思維窄化，使學生從主觀意識抵觸動點問題，解題思路不清晰.

3 教學應對措施

3.1 解決動點問題的方法要多樣化

教師在平時引導學生解決動點問題時，在已有教學方法的基礎上，不斷探究新的方法，引導學生一題多解，啟發式教學，在解題的過程中注意將數形結合的思想方法滲透到教學中.有不同解題方法的同學，在課堂進行交流和分享，可以讓學生掌握不同的解題方法，發散思維，這樣既能拓寬學生的思維方式，又能幫助學生回顧之前的知識，并逐步形成綜合運用知識的能力.

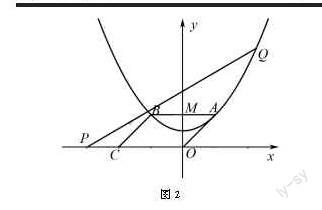
例如：在課堂講解中，學生們遇到了一個測試問題（如圖2）：二次函數的關系式是y=0.25x2+1，點C的坐標為（-4，0），平行四邊形OABC的頂點A、B在拋物線上，AB與y軸交于點M，已知點Q（x，y）在拋物線上，點P（t，0）在x軸上.當四邊形CMQP是一個以MQ、PC為腰的梯形時，找出t關于x的函數解析式和自變量x的取值范圍.

這道題是典型的二次函數動點問題，由點的運動形成特殊圖形，學生要理解題意，并且能夠綜合運用知識，梳理解題思路，找到恰當的解題方法，這道題有以下幾種解題方法：（1）解析法，根據題干給出的二次函數關系式得出對稱軸，進而求出點A與點M的坐標.接下來，連接CM并計算直線的CM解析式，并運用梯形上下底平行，獲得t關于x的函數解析式;（2）三角函數法，構建直角三角形，并使用三角函數進一步求解直角三角形;（3）相似法，可以運用題中已知的相似三角形得到相似比，或者結合題干信息來構造相似三角形，進而求解.因此，教師要多引導學生將知識融合到一起，經常在頭腦中形成知識網，善于挖掘多種方法解題.

3.2 與生活聯系，用輔助工具解題

數學與我們的生活密不可分，學之用之，將數學與實際生活相聯系，才能更加深入了解學習數學的意義，產生學習數學的濃厚興趣，對于知識形成探究的精神，能夠主動思考問題，可以利用數學思想和方法解題，例如：數形結合、類比、化歸、數學建模等.而這些都需要教師日常教學的引導和示范.在教學中，教師通過講解滲透數形結合和數學建模的思想和方法.例如，在尋找二次函數關系式時，繪制二次函數的圖象并結合圖象進行解釋將更加直觀.

3.3 引入多媒體、幾何畫板教學

二次函數動點問題難就難在綜合性和點的“運動”，學生不能在頭腦中形成運動軌跡，因此對于多種情況考慮得不充分，如果教師可以在課堂上可以運用現代化教學手段，例如：多媒體、動態幾何畫板等.講解過程中，將直觀的圖形與講解相結合，運用動態畫板演示出點的運動軌跡，以及在運動中形成的圖形，會讓學生印象深刻，理解性更強.使用多媒體教學不僅能吸引學生的注意力，而且可以帶著問題觀察和思考，通過自身的觀察得到答案，提升學生的學習數學的成就感，并理解形成過程，了解內涵，更好的應用. 運用這對學生將來解決二次函數的運動點問題有很大幫助，不再困難.

4 動點問題解題類型與教學要求

4.1 動點問題解題類型

二次函數動點問題可以分類解決，掌握問題的類型以后，可以幫助教師更有針對性地教學，有利于提高教學效率和改善教學效果.

4.1.1 根據問題分類

從問題出發進行分類，二次函數動點問題主要可以分為三種類型： 求最值問題，求函數表達式的問題，求動點的存在性問題.

4.1.2 根據動點的個數分類

從動點的個數來看，可以把二次函數動點問題分為兩類：單動點問題和雙動點問題.

4.1.3 根據函數與圖形的結合分類

就函數和圖形之間的結合問題來說，可以包括：函數與矩形和四邊形結合，二次函數與直線結合問題，與橢圓結合問題，以及與三角形結合問題等等.

4.2 動點問題的教學要求

教師在提問時，對以下兩個方面的教學要加強.

4.2.1 注重知識點間的銜接

由于在二次函數動點問題中，會涉及初中三年學習的知識點，因此要求學習者不僅僅需要掌握各知識點之間的聯系，同時還要靈活運用，從而了解該問題中的變量與方程相關，從而為動點問題解決奠定良好的基礎.

4.2.2 加強各問題之間的聯系

動點問題通常至少由三個問題所構成，而各個問題間往往會產生遞進關系，因而聯系更加密切.比如，二次函數關系式就是后面求最值問題的基石，也可以為存在性問題做好了鋪墊.因此學生在做題時如果可以了解問題之間的連接關系，并且能夠恰當地運用，也就能夠提高解動點問題的效果.

5 結語

二次函數動點問題是初中數學學習的重點和難點，也是學生在初中數學學習中的痛點，在教學過程中，教師要不斷練習與探究此類問題，不斷探究新的解題方法，做到一題多解，讓學生在遇到此類問題時能夠產生源源不斷的解題思路，逐步消除學生的畏難心理，以積極的態度解決此類問題，提高綜合運用知識的能力和解決問題的能力，形成數學的核心素質，并改善初中數學動點問題學習的現狀.

參考文獻：

[1]姚璐.基于問題解決的初中數學課堂教學設計——以“二次函數的應用”教學為例[J].數學教學通訊.2019（02）

[2]沈啟芳.初中數學中動點問題的教學研究[J].新教育時代電子雜志，2019（36）：1.

[3]周航.初中數學動點問題的解題策略探討[J].新課程（中學），2015（7）：102-103.