構造臨界圖形，直觀分析參數取值范圍

陳贇

有些新定義問題綜合了平移變換的內容。隨著平移的位置不同，往往會有多處臨界情形，我們如果能準確構造出臨界圖形，就能直觀分析參數的取值范圍。下面結合一道新定義問題，解讀新定義，構造臨界圖形，讓“思維可視化”。

例題 在平面直角坐標系xOy中，對于已知點P和圖形W，若對圖形W上任意兩點M和N，都有PM≤3PN成立，則稱圖形W為點P的“關聯圖形”。

已知⊙T的圓心為T（t，0），半徑為2，直線y=x-1與x軸、y軸分別交于G、H兩點，若在線段GH上存在點P，使得⊙T是點P的“關聯圖形”，分析t的取值范圍。

【思路解析】解題之前，先要厘清新定義中PM、PN需要滿足的條件，除了PM≤3PN以外，還需要理解當PM取最大值，PN取最小值時，PM、PN滿足PM≤3PN，這樣才符合新定義所說的“關聯圖形”。

【思路突破】先思考對于半徑為2的⊙T，平面內一點P到圓上的點的最大距離和最小距離有怎樣的特點？應該作直線PT，與圓相交于兩點，進而分析出它們是否符合新定義的不等式要求。由點和圓的三種位置關系來分類討論，厘清點P的可能位置，是“破題”關鍵。下面，我們構造示意圖分析。

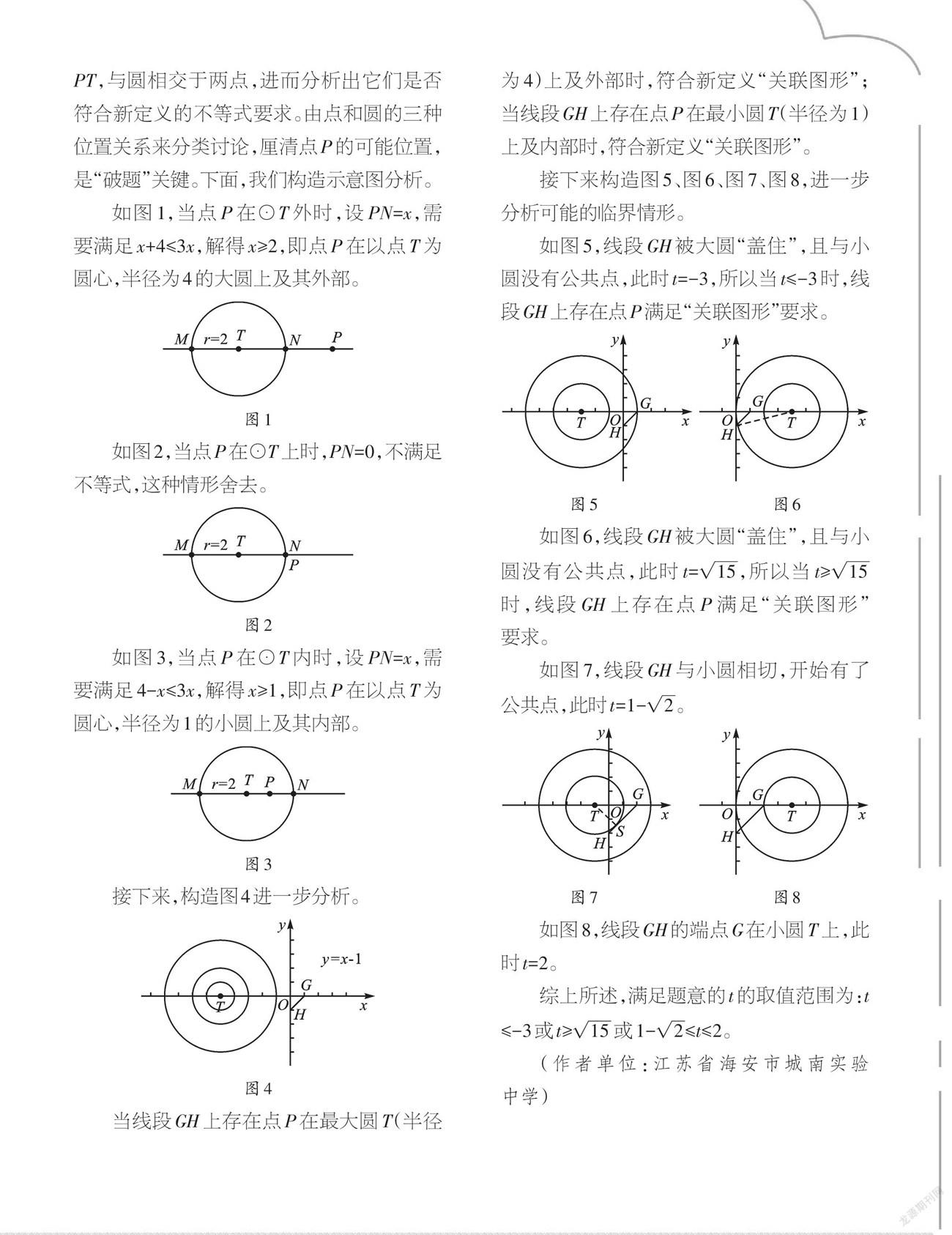
如圖1，當點P在⊙T外時，設PN=x，需要滿足x+4≤3x，解得x≥2，即點P在以點T為圓心，半徑為4的大圓上及其外部。

如圖2，當點P在⊙T上時，PN=0，不滿足不等式，這種情形舍去。

如圖3，當點P在⊙T內時，設PN=x，需要滿足4-x≤3x，解得x≥1，即點P在以點T為圓心，半徑為1的小圓上及其內部。

接下來，構造圖4進一步分析。

當線段GH上存在點P在最大圓T（半徑為4）上及外部時，符合新定義“關聯圖形”;當線段GH上存在點P在最小圓T（半徑為1）上及內部時，符合新定義“關聯圖形”。

接下來構造圖5、圖6、圖7、圖8，進一步分析可能的臨界情形。

如圖5，線段GH被大圓“蓋住”，且與小圓沒有公共點，此時t=-3，所以當t≤-3時，線段GH上存在點P滿足“關聯圖形”要求。

如圖6，線段GH被大圓“蓋住”，且與小圓沒有公共點，此時t=[15]，所以當t≥[15]時，線段GH上存在點P滿足“關聯圖形”要求。

如圖7，線段GH與小圓相切，開始有了公共點，此時t=1-[2]。

如圖8，線段GH的端點G在小圓T上，此時t=2。

綜上所述，滿足題意的t的取值范圍為：t≤-3或t≥[15]或1-[2]≤t≤2。

（作者單位：江蘇省海安市城南實驗中學）