緊扣數數本質 促進概念形成
——《小數的初步認識》教學實踐與思考（一）

文 王越娟

【教學內容】

人教版三年級下冊第七單元第一課時。

【教前思考】

小數亦稱十進小數，是實數的一種特殊表現形式。三年級學生對小數已有一定的生活經驗，但大多是依附于商品價格、長度、氣溫等認識，離開這些現實情境，小數便成了抽象的存在，讓人難以理解。那么，如何幫助學生更好地認識小數呢？

史寧中教授在《〈數學課程標準（2011年版）〉解讀》中指出：“小數產生有兩個前提，一是十進制記數法的使用，二是分數概念的完善。”而現行的小學數學各版本教材在第一次“認識小數”時大都強調“小數是十進分數的另一種表示方法”，并溝通了整數、分數與小數之間的聯系。人教版教材在“分數的初步認識”學習的基礎上，安排了“小數的初步認識”，并以“長度”作為主要的學習素材，試圖通過分數意義的遷移來實現學生對小數意義的理解，如“1 分米是米，可以寫成0.1 米；3 分米是米，可以寫成0.3 米。”但看似“一脈相承”的問題情境，學生在學習過程中卻有些“生硬”。為何？因為之前在初次認識分數時，更傾向于對“關系”意義的認知，（如下圖）而在初次認識小數時，則更傾向于聯系分數的有關“具體量”的意義。同時，學生在對于生活中具體量的體驗中，“用分數”的經驗并不豐富。因此，僅僅借助分數的“具體量意義”來突破對小數的理解，顯得并不恰當。

通過對數學史的了解，我們也發現，相較于分數，小數似乎與十進制計數法更有淵源。而數學家華羅庚早已明確提出“數是數出來的！”他認為：小數是十進分數的簡寫形式，但簡寫不是終極目的，終極目的是為了分數也能像整數那樣“滿十進一、退一作十”。整數、小數、分數因為十進位值、數的數數本質而得到了貫通。因此，我們既要重視并利用好“分數”這一基礎對“認識小數”的積極作用，同時更應溝通好計數方法一致的整數和小數。一方面，通過具體“量”的導引幫助學生理解小數的現實意義；另一方面，也要適時放手，讓學生嘗試用自己的方式去表征和探究小數，主動質疑、實踐、感悟和發現。

【教學過程】

一、重溫“數數”，激活“計數單位”的經驗

1.重溫“數數”。

師：同學們，在數數時咱們都請哪些數學工具幫過忙呀？

生：小棒、計數器、圓片、方塊等等。

（根據學生的回答，課件出示，幫助學生更好地回憶）

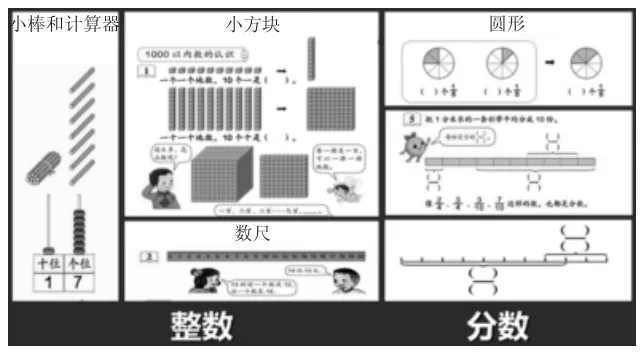
師：是啊，借助這些數學工具我們認識了很多整數和分數，就像我國著名的數學家華羅庚爺爺說的那樣：“數是數出來。”今天，我們就來數“小數”。

2.讀寫“小數”。

師：請在學習紙上寫一個小數，并觀察有什么特別的地方。

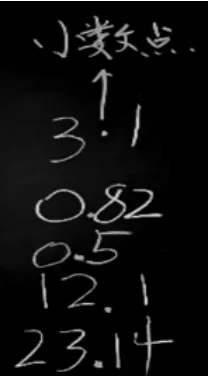
生：都有“小數點”。

師：對，正是這個“小數點”把小數分成了左右兩個部分。一起讀一讀……

二、探究“新數”，促進“計數經驗”的遷移

1.提出質疑。

師：（課件出示“0.1”）看到這個小數，你有什么疑問嗎？

生：為什么要有0.1？有1 還不夠嗎？

生：0.1 表示多大呢？

生：0.1 是怎么來的？

生：0.1 和1 有什么關系？

師：大家提的問題都非常值得我們思考，接下來就請帶著這些問題來研究這個看似簡單又有點神秘的“0.1”吧！

2.自主表征。

師：（出示四種學習材料）請你任選一種或幾種材料，表示出“0.1”。

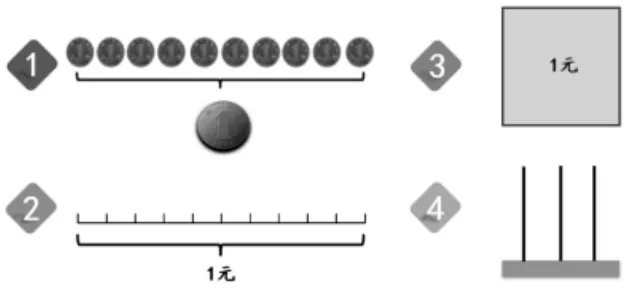
（學生自主表征，教師巡視收集典型素材）

3.交流反饋。

●材料1 反饋：基于“1 角＝0.1元”的經驗，借助硬幣表征“0.1”。

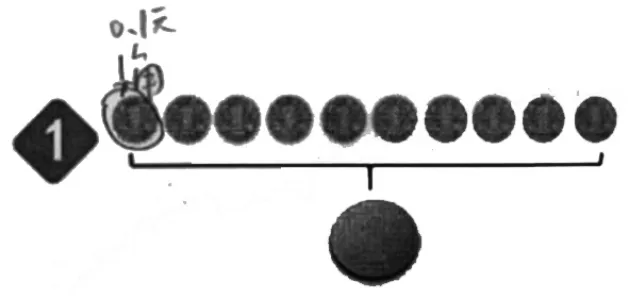
師：他找對了嗎？

生：找對了，1 角＝0.1 元。

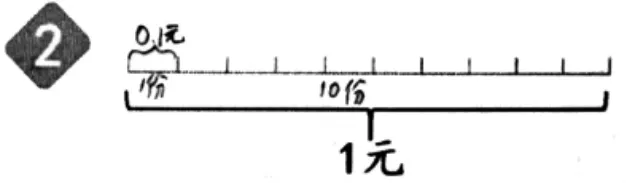
師：為什么這一段表示0.1 元？

生：1 元里面有10 個1 角，這里正好把1 元平均分成了10 份，其中的1 份就表示1 角，也就是0.1 元。

師：在他說的這段話中，有什么值得特別注意的？

師：除了這一段表示0.1，還有沒有0.1 了？

生：剩下的每一份都表示0.1。

●材料3 反饋：借助正方形表征“0.1”，關注錯例強化“十分”。

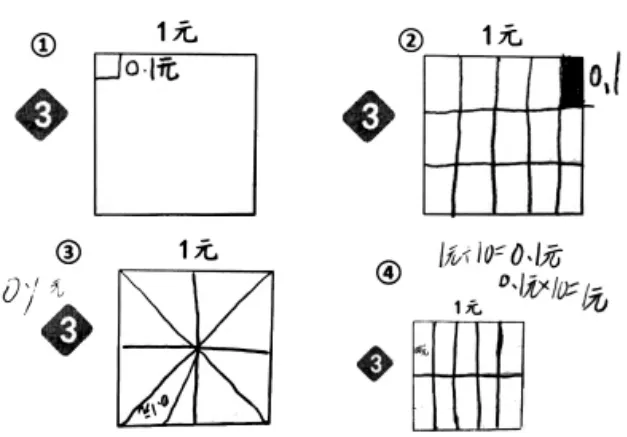
師：仔細觀察這幾幅圖，請大家發表意見。

生：怎么確定①里面畫的這一小塊表示0.1？

生：按照他這樣表示，我估計這里大約有25 個0.1，合起來超出1 了。

生：②和③雖然分了，但一個15 份、一個9 份，而且還不平均，也都不對。

生：我贊同④，他不僅分對了，還寫了算式，表示得很清楚。

師：同學們，能不能用一句話來概括自己的判斷標準？

生：就是看有沒有平均分成10 份。

師：把1 平均分成10 份，其中的1 份還可以用哪個數來表示？

●材料4 反饋：借助計數器表征“0.1”，打通整數與小數的“十進”關系。

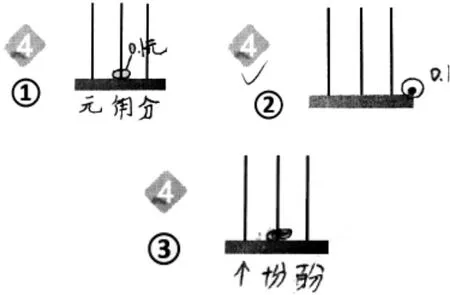
師：看了這些同學的作品，有沒有想問的？

生1：我對②有疑問，這個是計數器，你的0.1 怎么在計數器的外面？

生2：計數器的最右邊是個位，0.1 比1 小，只有十分之一，所以不能把珠子撥在個位上，只能在個位的右邊。

生1：那我們在計數器上再加一根上去不就得了。

生3：我本來看不懂③，現在有點明白了。其實和②是一個意思，只不過③把最左邊那個位置看作個位，這樣中間一位就可以表示0.1，如果再分下去，還可以繼續增加位置，就是他寫的百分。

生4：我覺得后面兩種表示比第一種更好，不用想元、角、分，也可以表示出比0.1 更小的小數。

師：真的嗎？那我們就拿真的計數器來試一試。我們先像③那樣把個位定好，一起數一數。

（1、2、3……9、10）

生：滿十進一，十位上撥1。

（10、20、30……90、100）

生：又滿十進一了，在百位上撥1。

師：如果我想把這1 個百還回去，怎么撥？

生：把百位上的1 撥回去，十位上撥10。

師：要把這1 個十還回去，怎么撥？

生：把十位上的1 撥回去，個位上撥10。這就是退一作十！

師：很好！那現在剩下1 個一，我還想還回去，有辦法嗎？

生：還是一樣，把1 撥回去，個位右邊撥10。

師：這里的1 表示多少？

生：0.1。

師：再右邊一個位置撥1 呢？

生：0.01。

師：還能再往右退一當十嗎？

生：可以呀，數不完的。

師：回顧剛才在計數器上數小數、數整數的過程，有什么發現？

生：數小數和數整數的方法是一樣的，每滿10 個就要向前進一，反過來，退下來的1 又可以換成10。

生：整數和小數是連著的，它們就像一家人。

4.抽象釋疑。

師：（課件回到四種材料）無論在哪種材料里，大家都找到了0.1。那么，現在你對一開始的幾個疑問有想法了嗎？0.1 是怎么來的？它和1 有什么關系？

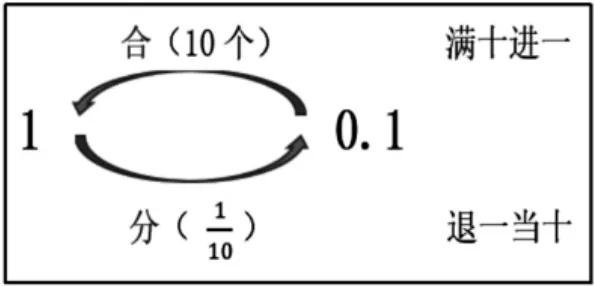
生：0.1 是從1 里面分出來的。

生：0.1 是把1 平均分成10份，表示其中的1 份，也就是反過來10 個0.1 就能合成1 個一。

師：原來，0.1 和1 之間就是這樣一種“分與合”的關系呀！你們真能干！

三、拓展“小數”，感悟“計數活動”的本質

1.辨析：是0.3 米嗎？

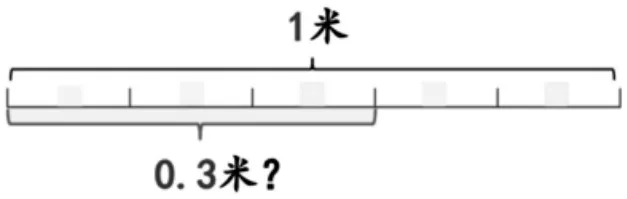
師：請判斷并說明理由。

生：不是0.3 米，因為這里沒有把1 米平均分成10 份，所以每一份不是0.1 米，3 份也不是0.3 米。

生：在這個基礎上繼續分，也就是這里的每一份再平均分成2份，就能看出這不是0.3 米，而是0.6 米。

2.拓展：看圖直接說出小數。

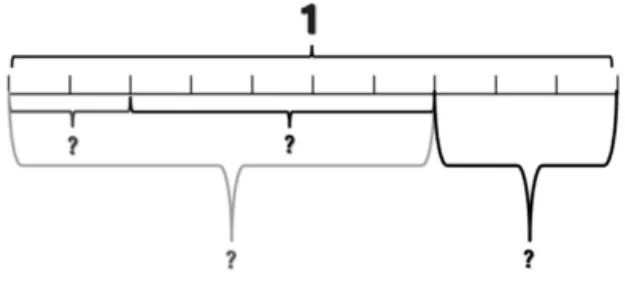
（滲透簡單的小數加減法）

3.提升：根據需要合理推想。

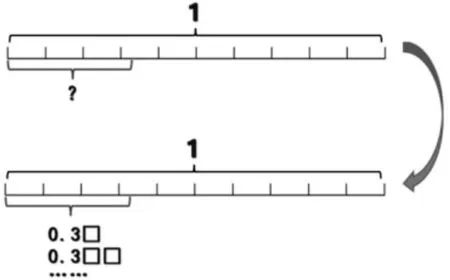
（滲透對兩位小數、多位小數及精確度的初步認知）

4.總結。

師：我們數著數著就把這么多“小數”數出來了，數著數著就把“小數”給數明白了。在今天的“數數”活動中，你還有哪些發現或體會嗎？

……

師：同學們說得太棒了！其實，今天我們對小數的認識只是冰山一角，往后，我們還將通過“數數”探索和發現更多的小數。