串并聯(lián)系統(tǒng)中休止時(shí)間的隨機(jī)比較
羅天奇
(蘭州石化職業(yè)技術(shù)大學(xué),蘭州 730070)
將元件分配給串聯(lián)系統(tǒng)中的元件是一種常見(jiàn)的方法,被廣泛應(yīng)用于提高系統(tǒng)的可靠性。在實(shí)際情況中,通常遇到兩類(lèi)基本系統(tǒng):由舊元件組成的系統(tǒng)和舊的系統(tǒng)。過(guò)去幾十年,系統(tǒng)熱冗余分配問(wèn)題被許多作者研究。Boland等[1-2]應(yīng)用幾種隨機(jī)序研究串并聯(lián)系統(tǒng)的這一問(wèn)題,并取得了一些奠基性成果。后來(lái),Singh和Misra[3]沿這一方向繼續(xù)研究。最近,Valdés和Zequeira[4-5],Yan和Luo[6]進(jìn)一步豐富了現(xiàn)有成果(其它更多的相關(guān)研究可參考文獻(xiàn)[7-9])。前面的作者只考慮串聯(lián)系統(tǒng)冗余分配問(wèn)題,而我們考慮將舊元件分配到舊系統(tǒng)與新元件分配給新系統(tǒng)的休止時(shí)間問(wèn)題以及由兩個(gè)元件組成的串聯(lián)系統(tǒng)的休止時(shí)間問(wèn)題,也就是舊元件分配到舊系統(tǒng)系統(tǒng)失效所需的時(shí)間與新元件分配給新系統(tǒng)系統(tǒng)失效所需的時(shí)間哪個(gè)更長(zhǎng)。






上面幾種隨機(jī)序之間有如下的蘊(yùn)含關(guān)系:X≤hrY?X≤stY,X≤rhY?X≤stY。關(guān)于隨機(jī)序更加詳細(xì)的討論請(qǐng)參閱參考文獻(xiàn)[10]。Ruiz和Navarro[11]定義了由條件隨機(jī)變量Xt=(t-X|X≤t)定義的休止時(shí)間(IT),表明了在元件壽命小于或等于t的情況下,失效所需的時(shí)間,隨機(jī)變量Xt也可稱(chēng)為反向剩余壽命(或失效后的時(shí)間)。
具有壽命t≥0元件的休止時(shí)間表示為X(t)=(t-X|X≤t),舊元件組成的串聯(lián)系統(tǒng)min(X(t),Y(t))、并聯(lián)系統(tǒng)max(X(t),Y(t))、舊系統(tǒng)(min(X,Y))(t)、(max(X,Y))(t)。Li和Lu[12]證明X和Y同分布,min(X(t),Y(t))≤st(min(X,Y))(t),max(X(t),Y(t))≤hr(max(X,Y))(t)。Yan和Luo[6]證明X和Y不同分布max(X(t),Y(t))≥hr(max(X,Y))(t)。本文基于Yan和Luo[6]的工作,進(jìn)一步研究冗余系統(tǒng)min(max(X(t),Z(t)),Y(t)),(min(max(X,Z),Y))(t)以及max(X(t),Y(t))≥rh(max(X,Y))(t),max(X(t),Y(t))≥lr(max(X,Y))(t)隨機(jī)率序下的的隨機(jī)比較問(wèn)題。
1 一個(gè)元件分配到兩個(gè)元件組成的串聯(lián)系統(tǒng)組成串并聯(lián)的休止時(shí)間

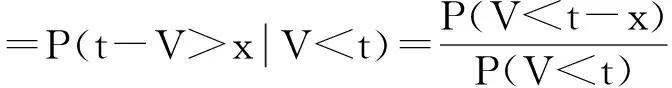
下面的例子顯示在普通隨機(jī)序下并不能得到V(t)≤V(t)或V(t)≥V(t)。


特別地,x=0.05時(shí),P(V(t)>x)=0.998 447 595,P(V(t)>x)=1.004 387 475,即V(t)≤stV(t);x=0.15時(shí),P(V(t)>x)=0.995 449 221,P(V(t)>x)=0.983 009 65,即V(t)≥stV(t)。







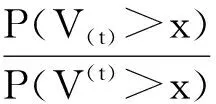
接下來(lái)的定理顯示在一定條件下V(t)與V(t)可以隨機(jī)比較。

證明V(t)和V(t)的生存函數(shù)分別為

設(shè)g(x)=F(t)-F(t-x)+2F(t-x)[F(t)]2-F(t)F(t-x)=F(t)-F(t-x)(2F(t)+1)(1-F(t)),

g′(x)=f(t-x)(2F(t)+1)(1-F(t))≥0,
gmin(x)=g(0)=F(t)-F(t)(2F(t)+1)(1-F(t))=F2(t)(2F(t)-1),


證明V(t)和V(t)的生存函數(shù)分別為

要證明V(t)≥stV(t),只需證明P(V(t)>x)≥P(V(t)>x),
P(V(t)>x)-P(V(t)>x)

證明完成。
下面的定理顯示一定條件下在失效率序下V(t)與V(t)的隨機(jī)比較。
定理3 設(shè)隨機(jī)變量X1,X2和X相互獨(dú)立且有相同分布F(x),則V(t)≥hrV(t)。
證明V(t)和V(t)的生存函數(shù)分別為



證明完成。
定理4 設(shè)隨機(jī)變量X1,X2和X相互獨(dú)立,且F1(t-x)F1(t-x)=F2(t-x)=F(t-x)F(t-x),則V(t)≥hrV(t)。
證明V(t)和V(t)的生存函數(shù)分別為


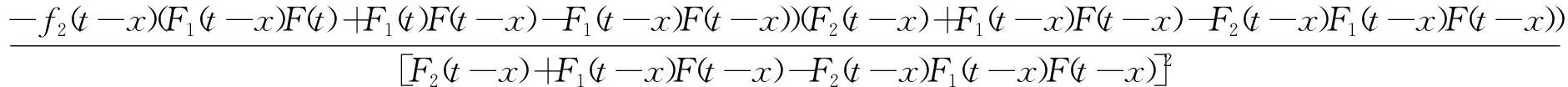

證明完成。
下面的定理顯示一定條件下在普通隨機(jī)序下V(t)與V(t)的隨機(jī)比較。

證明要證明V(t)≥stV(t),只需證明P(V(t)>x)≥P(V(t)>x),
P(V(t)>x)-P(V(t)>x)



P(V(t)>x)-P(V(t)>x)

證明完成。
2 兩個(gè)元件分配到兩個(gè)元件組成的串聯(lián)系統(tǒng)組成串并聯(lián)系統(tǒng)的休止時(shí)間


下面的定理顯示一定條件下在普通隨機(jī)序下U(t)與U(t)的隨機(jī)比較。
定理6 設(shè)隨機(jī)變量X1,X2和Y1,Y2相互獨(dú)立有相同分布F(x),則U(t)≤stU(t)。
證明要證明U(t)≤stU(t),只需證明P(U(t)>x)≥P(U(t)>x)

證明完成。
3 并聯(lián)系統(tǒng)的休止時(shí)間
設(shè)X和Y為相互獨(dú)立隨機(jī)變量,其分布函數(shù)分別為F(x)和G(x),設(shè)并聯(lián)系統(tǒng)休止時(shí)間max(X,Y)(t),max(X(t),Y(t))分布函數(shù)分別為
F(x)=P(max(X,Y)(t)≤x)=1-P(t-max(X,Y)>x|max(X,Y) 接下來(lái)在反失效率序并聯(lián)系統(tǒng)的休止時(shí)間進(jìn)行比較。 定理7 設(shè)隨機(jī)變量X,Y相互獨(dú)立,則max(X,Y)(t)≤rhmax(X(t),Y(t))。 證明完成。 接下來(lái)在似然比序并聯(lián)系統(tǒng)的休止時(shí)間進(jìn)行比較。 定理8 設(shè)隨機(jī)變量X,Y相互獨(dú)立(不必同分布),則max(X,Y)(t)≤lrmax(X(t),Y(t))。 本文僅研究?jī)蓚€(gè)元件組成的串聯(lián)系統(tǒng)獨(dú)立情況下,將一個(gè)元件和兩個(gè)元件分配到串聯(lián)系統(tǒng)中組成串并聯(lián)系統(tǒng),得到了休止時(shí)間的隨機(jī)比較結(jié)果;對(duì)于其它兩個(gè)元件冗余分配的剩余壽命和休止時(shí)間問(wèn)題可作進(jìn)一步的研究工作。 致謝:感謝在本文寫(xiě)作過(guò)程中西北師范大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)院顏榮芳教授給予的幫助!
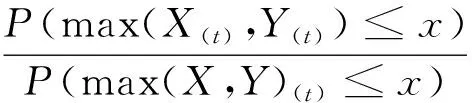



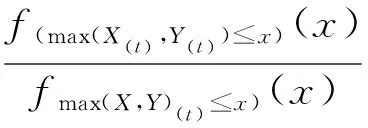





4 結(jié) 語(yǔ)

