小學高段學生符號意識測試問卷編制研究

鞏子坤 吳敏霞 趙雨晴

【摘? ?要】符號意識是重要的數學核心素養之一。了解、測量學生的符號意識及其發展水平，有助于培養學生的符號意識，發展學生的數學核心素養。基于相關研究成果，編制了符合小學4～6年級學生生理及心理特質的符號意識測試問卷。通過多次大樣本測試，結合探索性因素分析、驗證性因素分析等結果，不斷進行修訂，最終形成的問卷包含符號理解、符號表示、符號運算、符號推理四個維度，共43道題。該問卷具有良好的信效度，可以作為評估4～6年級學生符號意識的有效工具。

【關鍵詞】4～6年級學生;符號意識;問卷編制

一、引言

符號意識，是學習者將數學知識抽象成對應的數學符號的認知活動，是解決數學問題過程中表現出來的數學核心素養[1]，其形成直接影響學生數學能力的發展。然而，目前在教學中沒有專門的測試來檢驗學生的符號意識。四年級是從經驗型思維向理論型思維轉化的開始，是學生符號意識發展水平的關鍵節點[2-3]。本研究在已有研究的基礎上，對符號意識的內涵進行了再認識，編制了符號意識測試問卷，為探明小學4～6年級學生的符號意識及其發展水平提供了基本工具。

二、問卷編制與實施

（一）符號意識內涵解讀

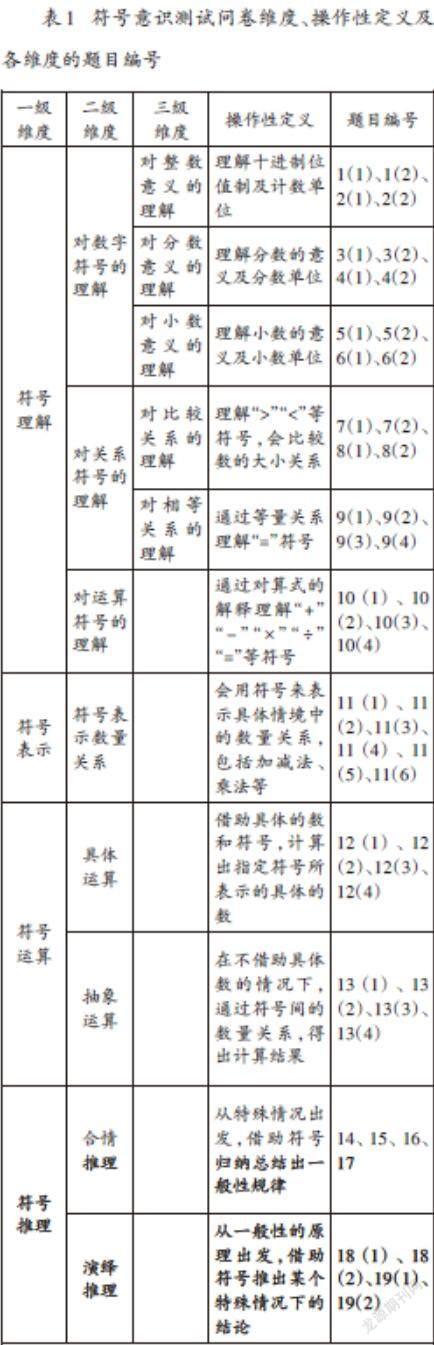
我國對符號意識的研究晚于西方。以Abraham Arcavi[4]為代表的研究成果為國內進行符號意識研究奠定了基礎。《義務教育數學課程標準（2022年版）》中指出符號意識主要是指能夠感悟符號的數學功能。知道符號表達的現實意義;能夠初步運用符號表示數量、關系和 一般規律;知道用符號表達的運算規律和推理結論具有一般性;初步體會符號的使用是數學表達和數學思考的重要形式。史寧中教授從行為的角度對課標進行了解讀：理解符號意義和運用符號進行表達，通過符號操作得到一般性結論，強調學生學習數學符號的觀念對數學發展的重要性。[5]李艷琴和宋乃慶認為，符號意識是指學生在表示數學概念、數學關系等符號的感受、體會、認識、理解、運用等方面的反應。[6]基于學者們對符號意識的解讀，將符號意識分為符號理解、符號表示、符號運算、符號推理四個維度。

（二）問卷理論結構構建

我們基于對符號意識維度的劃分，確定符號意識問卷的理論結構。為更好地編制符號意識測試題目，結合4～6年級學生的學習內容，嘗試對各維度給出操作性定義，如表1所示。

（三）問卷測試題目編制

在設計題目的過程中，征求一線教師關于小學4～6年級學生的認知水平及題目呈現形式等的建議，同時征求了數學教育專家和優秀的小學數學教研員的意見，不斷地對問卷進行修訂，初步形成了符號意識測試問卷一。

（四）樣本選取與問卷回收

為保證符號意識問卷的信效度，選取了三個樣本分別進行測試。后一次測試問卷是基于前一次測試的數據分析結果進行修訂后得到的。

使用問卷一對樣本一進行測試，該樣本來自杭州市J區某學校學習層次有明顯差別的五年級學生，共4人。回收問卷共4份，其中有效問卷為4份，有效率達100%。

使用問卷二對樣本二進行測試，該樣本來自杭州市X區某學校四、五、六年級學生，共490人。回收問卷共490份，其中有效問卷為386份，有效率達78.8%。

使用問卷三對樣本三進行測試，該樣本來自杭州市G區某學校四、五、六年級學生，共450人。回收問卷共450份，其中有效問卷為402份，有效率達89.3%。

（五）數據分析工具與方法

每道題正確記1分，錯誤記0分。先利用SPSS對樣本一數據進行統計分析，借助訪談了解學生對題目的理解情況，根據反饋修訂問卷;再利用SPSS對樣本二數據進行項目分析和探索性因素分析，以便得到問卷的主成分，調整問卷的理論結構及測試題目;最后利用AMOS對樣本三數據進行驗證性因素分析，確認問卷理論結構的合理性。

三、問卷預測與修訂

（一）問卷預測

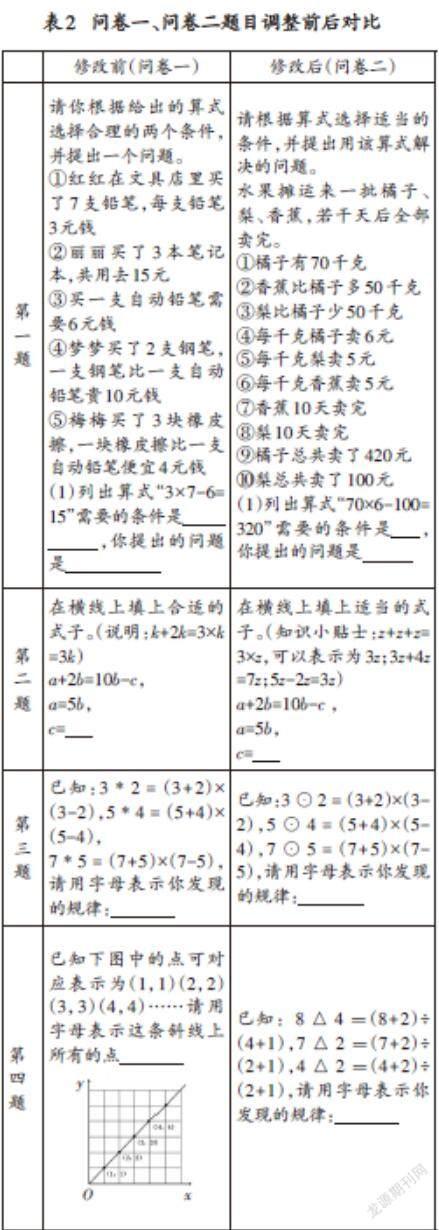
對樣本一收集到的數據進行整理、錄入。先結合訪談了解學生對題目存在困惑的地方，進而對4道題目進行調整與完善，形成問卷二。修改前后的題目如表2所示。

第一題屬于“對運算符號的理解”維度，修改前的題目供學生思考的空間較小，部分學生會通過觀察選擇出現過相同的數的條件，而不是在理解算式的意義之后選擇適用的條件。因此通過修改提供的條件，使得提供的條件中多次出現相同的數來改變這一情況。

第二題屬于“抽象運算”維度，難度較大，因此在題目后給予一定的提示，但“k+2k=3×k=3k”連等的算式不利于學生對“數字乘字母”這種形式的理解。因此將提示改為“z+z+z=3×z”，指明“3×z，可以表示為3z”，并通過舉例加深學生的理解。

第三題屬于“合情推理”維度，由于“*”與乘號較像，將“*”改為“⊙”。

第四題也屬于“合情推理”維度，該題以坐標的形式出現，超出了學生的認知范圍，因此改為與該維度其他題目形式接近的題目。

（二）項目分析

對樣本二收集到的數據進行項目分析。先用臨界比率法刪除不具有高低分組顯著性差異的題目。再用題總相關法對各題得分與總得分之間進行相關分析，意在刪除與總得分相關系數不顯著的題目。經過項目分析，問卷二無刪題，仍有46道題目。

（三）探索性因素分析

基于項目分析，對樣本二數據進行探索性因素分析。KMO值為0.907，Bartlett球形度檢驗相關性顯著（p<0.01），表明樣本二數據很適合做因子分析。因此，使用主成分分析法和最大方差旋轉法確定問卷的因子數和題目。經探索性因素分析，主成分與符號意識問卷的理論結構一致，刪除1（1）、2（1）、2（2）、4（1）、4（2）、8（2）、9（1）共7道題。為更好地反映測試內容，需使各維度題目在3道或以上，故根據分析結果增加整數、分數維度的同質性題目各2道。1B464F7B-5FE0-4E50-B08C-3B7275142D42

如“對分數意義的理解”維度，刪除了題目“一根繩子長2米，將它平均分成3段，每段占全長的? ? ? ? ? ? ? ?，每段長? ? ? ? ? 米”，增加了題目“一根繩子長3米，剪去2米，剪去的占全長的? ? ? ? ? ，剩余的占全長的? ? ? ? ? ”。這保證了分數測試維度題目的同質性。

修訂后形成最終的測試問卷三，包含43道題，詳見附錄。

四、問卷檢驗與確定

（一）驗證性因素分析

對樣本三收集的數據進行驗證性因素分析，檢驗實際數據與理論模型的擬合程度。首先構建一階兩兩相關模型，根據分析結果進行殘差修正，在各指標基本達到模型適配標準后再構建二階模型。同理構建三階模型。三種模型的各擬合指標如表3所示。

從擬合結果來看，隨著結構模型的不斷改進，各指標擬合得越來越好，且符號意識三階結構模型的擬合指標基本達到了檢驗標準。因此，實際數據與該模型的適配情況良好，該符號意識理論結構和題目編制是比較合理的。本研究設計的小學4～6年級學生符號意識測試問卷的結構模型如圖1所示。

（二）問卷的信度和效度分析

1.信度分析

信度是效度的前提條件。采用Cronbachs α系數檢驗問卷的內部一致性，考察問卷的每個題目是否測試了相同的內容或特質。數據表明問卷具有很好的內部一致性（如表4）。

2.效度分析

效度是指測試工具或手段能夠準確測出所需測量事物特質的程度。本研究主要分析問卷的內容效度和結構效度。

（1）內容效度

內容效度指的是測試題目對有關內容取樣的適用性。在問卷形成后，邀請4位專家對問卷題目與其所屬維度的相關性做出評價，即在“‘1表示完全無關、‘2表示有點相關、‘3表示較強相關、‘4表示完全相關”的四點量表上做出判定。依據評價標準（K*：0.40～0.59為一般，0.60～0.74為良好，0.74～1.00為優秀[7]），35道題為優秀，8道題為良好。進一步計算，結果顯示S-CVI/UA為0.81，S-CVI/Ave為0.95。根據S-CVI/UA不低于0.80，S-CVI/Ave應達到0.90的標準[8]，該符號意識問卷的內容效度較好（表5）。

（2）結構效度

結構效度指的是測試結果體現出來的某種結構與理論結構之間的一致性。從驗證性因素分析的結果來看，RMSEA在0.08以下，CFI等在0.9以上，因此擬合的三階模型是一個“好模型”[9]，該符號意識問卷的結構效度達到要求。

五、討論

本研究重在編制小學4～6年級學生的符號意識測試問卷。相較于團隊已有的研究成果，即“小學一年級學生符號意識測試問卷”和“小學2～3年級學生符號意識測試問卷”，以及目前的研究成果，本問卷編制的進步之處主要體現在以下兩個方面。

（一）問卷理論結構更完善

三份問卷一脈相承，均包含符號理解、符號表示、符號推理、符號運算四個維度。隨著學生認知水平的提高及知識量的增加，本問卷對結構進行了完善。特別是針對符號理解維度，將學生對數字符號的理解細分為對整數、分數、小數意義的理解;對關系符號的理解細分為對比較關系、等于關系的理解，同時增設對運算符號的理解這一考察維度。在一定程度上，本次問卷考察內容更細致，理論結構更完善。

（二）問卷編制過程更嚴謹

前兩份問卷選取的樣本量較小，數據分析易出現誤差。為減少這一誤差，本次問卷編制過程中選取了大樣本用于探索性因素分析，并選取大樣本對最終問卷進行驗證性因素分析及信效度檢驗。因此，本次問卷編制過程更嚴謹、分析方法更科學。

六、結論

本研究編制的“小學4～6年級學生符號意識測試問卷”理論結構更完善，編制過程更嚴謹，且具有較好的信效度。因此，本問卷可有效測試小學4～6年級學生的符號意識，也可為小學高段學生符號意識評價體系的形成及相關研究提供參考。

參考文獻：

[1]朱立明，馬云鵬.“數學符號意識”研究：內涵與維度[J].教育理論與實踐，2015，35（32）：6-8.

[2]鄭君文，張恩華.數學學習論[M].南寧：廣西教育出版社，1996：90.

[3]朱立明.義務教育階段學生數學符號意識發展水平研究[D].長春：東北師范大學，2017.

[4]Abraham A.Symbol Sense：Informal sense-making in formal mathetics [J].For the learning of mathematics，1994：3.

[5]史寧中.義務教育數學課程標準（2011年版）解讀[M].北京：北京師范大學出版社，2012：84-85.

[6]李艷琴，宋乃慶.小學低段數學符號意識的含義及其表現形式[J].課程·教材·教法，2016（3）：92-97.

[7]榮泰生.AMOS與研究方法[M].重慶：重慶大學出版社，2009（3）：128.

[8]史靜琤，莫顯昆，孫振球.量表編制中內容效度指數的應用[J].中南大學學報（醫學版），2012，37（2）：49-52.

[9]崔寶蕊，李健，王光明.初中生數學元認知水平調查問卷的設計與編制[J].數學教育學報，2018，27（3）：45-51.

附錄：問卷三

親愛的同學：歡迎參加這個小測試。請你仔細看題目，按照要求認真回答。測試的結果只用來做研究，與你的數學成績無關。1B464F7B-5FE0-4E50-B08C-3B7275142D42

1. 4500000000里有45個? ? ? 。60000000000里有600個? ? ? 。

2. 37200000里有3720個? ? ? 。

3. 一根竹竿長8米，截去5米，截去的占全長的? ? ? ，剩余的占全長的? ? ? 。

4. 一根繩子長3米，剪去2米，剪去的占全長的? ? ? ，剩余的占全長的? ? ? 。

5. 3.673中的左邊起第一個“3”表示3個? ? ? ，第二個“3”表示3個? ? ? 。

6. 1.57里面有15個? ? ? ，7個? ? ? 。

7. 填空。

（1）298+a > 305，a 是自然數，最小是? ? ? ? ? ?。

（2）435-b > 427，b 是自然數，最大是? ? ? ? ? ?。

（3）70×c > 258，c 是自然數，最小是? ? ? ? ? ?。

8. 填空。

（1）150-q = 90+12，那么q=? ? ? ? ? ?。

（2）16×4 = m÷10，那么m =? ? ? ? ? ? ?。

（3）216÷n= 3×8，那么n=? ? ? ? ? ? ?。

9. 請根據算式選擇適當的條件，并提出用該算式解決的問題。

水果攤運來一批橘子、梨、香蕉，若干天后全部賣完。

① 橘子有70千克。② 香蕉比橘子多50千克。

③ 梨比橘子少50千克。④ 每千克橘子賣6元。

⑤ 每千克梨賣5元。⑥ 每千克香蕉賣5元。

⑦ 香蕉10天賣完。⑧ 梨10天賣完。

⑨ 橘子總共賣了420元。⑩ 梨總共賣了100元。

（1）列出算式“70×6-100=320”需要的條件是? ? ? ? ? ? ? ? ，你提出的問題是? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 。

（2）列出算式“420÷6+50=120”需要的條件是? ? ? ? ? ? ? ? ，你提出的問題是? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 。

（3）列出算式“（70-50）×5=100”需要的條件是? ? ? ? ? ? ? ，你提出的問題是? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 。

（4）列出算式“（70+50）÷10=12”需要的條件是? ? ? ? ? ? ? ?，你提出的問題是? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?。

10. 在橫線上填上含有字母的式子。

（1）動物園里有a只兔子，有b只獅子，老虎的只數比兔子、獅子的總和少2只，動物園里有老虎? ? ? ? ? ? ? ?只。

（2）李明的爸爸買了c個蘋果，媽媽回來后吃了1個蘋果，李明放學回來后吃了d個蘋果，還剩下? ? ? ? ? ? ? 個蘋果。

（3）倉庫里有一批水泥，運走了5車，每車e噸，還剩下f噸，這批水泥共有? ? ? ? ? ? ? ?噸。

（4）小妍去商店買了3盒彩筆，共用去g元。如果買一盒鉛筆用的錢比買一盒彩筆的錢少h元，那么買一盒鉛筆需要用? ? ? ? ? ? ? ?元。1B464F7B-5FE0-4E50-B08C-3B7275142D42

（5）小華有鉛筆i支，小強有鉛筆j支。小華、小強的鉛筆總數是小剛的3倍，小剛有鉛筆? ? ? ? ? ?支。

（6）亮亮有k個梨，比麗麗多p個梨。如果花花的梨是麗麗的4倍，那么花花有? ? ? ? ? ? ? 個梨。

11. 在橫線上填上適當的數。

（1）27+13 = 54-a，a =? ? ? ? ? ? 。

（2）b+34 = 75-23，b =? ? ? ? ? ? 。

（3）56-10 = 17+c，c =? ? ? ? ? ? 。

（4）60-d= 16+34，d =? ? ? ? ? ?。

12. 在橫線上填上適當的式子。

（知識小貼士：z+z+z=3×z，可以表示為3z;3z+4z=7z;5z-2z=3z）

（1）a+2b = 10b-c，a = 5b，c =? ? ? ? ? ? 。

（2）3t+f = q-t， q = 8t， f =? ? ? ? ? ?。

（3）m-3r = 2r+n，m = 6r ，n =? ? ? ? ? ? 。

（4）8k-i = j+k ， j = 3k ，i =? ? ? ? ? 。

13.已知：3 ⊙ 2 =（3+2）×（3-2），5 ⊙ 4 =（5+4）×（5-4），7 ⊙ 5 =（7+5）×（7-5），請用字母表示你發現的規律：? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?。

14.已知：3@4=3×5-4×2，6@8=6×5-8×2，

9@5=9×5-5×2 ，請用字母表示你發現的規律：? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?。

15. 已知：? 8 △ 4 =（8+2）÷（4+1），7 △ 2 = （7+2）÷（2+1），4 △ 2 =（4+2）÷（2+1），請用字母表示你發現的規律：? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?。

16. 已知：（12-10）÷ 2 = 12÷2-10÷2 ，（18-12）÷ 3 = 18÷3-12÷3 ，（25-15）÷ 5 = 25÷5-15÷5 ，請用字母表示你發現的規律：? ? ? ? ? ? ? ? ? ? ? ? ? ? ?。

17. 規定兩種新運算“◎”和“○”，◎表示兩數之中取大數的運算，○表示兩數之中取小數的運算。如3◎5=5，7○10=7。請你算出以下兩個式子的結果。

（1）（9○12）+（28◎4）=? ? ? ? ? ? ? 。

（2）（19◎6）-（5○32）=? ? ? ? ? ? ? 。

18. 規定一種新運算“※”，a※b=a×a-b×b。請你算出以下兩個式子的結果。

（1） 9※（4※3）=? ? ? ? ? ? ? ?。

（2）（8※7）※5 =? ? ? ? ? ? ? ?。

（1. 杭州師范大學經亨頤教育學院? ?311121

2. 杭州市余杭區良渚杭行路小學? ?311101

3.浙江省杭州長河中學? ?310053）1B464F7B-5FE0-4E50-B08C-3B7275142D42