基于結(jié)構(gòu)元的模糊值Caputo分?jǐn)?shù)階微分方程

亢 琳，郭元偉

(1.江蘇師范大學(xué)科文學(xué)院基礎(chǔ)部，江蘇 徐州 221116；2.太原學(xué)院數(shù)學(xué)系，山西 太原 030032)

0 引言

眾所周知, Hukuhara微分[1]是研究模糊微分的基本方法之一,在不確定或不完全動(dòng)力系統(tǒng)中發(fā)揮了重要作用[2,3]。然而, 這種方法的缺點(diǎn)是模糊微分方程的解的支集會(huì)不斷增大。為解決這一問題 Bede[4]于2005年提出了廣義模糊微分、Stefanini[5]定義了廣義Hukuhara差，都較好地解決了模糊數(shù)H差的存在性問題，在此基礎(chǔ)上文獻(xiàn)[6～7]較系統(tǒng)地解決了廣義模糊微分方程解的存在性、唯一性等問題。模糊值分?jǐn)?shù)階微積分作為實(shí)值分?jǐn)?shù)階微積分的重要推廣已取得較豐富的成果。Allahviranloo[8]給出了廣義模糊值Caputo分?jǐn)?shù)階微分的定義,得到了與文獻(xiàn)[6]類似的結(jié)果。Lupulescu[9]定義了區(qū)間值分?jǐn)?shù)階微積分,討論了區(qū)間值Riemann-Liouville分?jǐn)?shù)階微積分、區(qū)間值Caputo分?jǐn)?shù)階微分的相關(guān)性質(zhì)。Shen[10]利用Banach壓縮映射原理研究了區(qū)間值Caputo分?jǐn)?shù)階微分方程解的存在唯一性問題。Ngo[11]利用逐步逼近法討論了廣義Lipschitz條件下Caputo型模糊泛函微分方程解的存在性、唯一性等問題，并給出具體的數(shù)值算法。郭嗣琮[12]于2004年提出了模糊結(jié)構(gòu)元理論,雖然基于結(jié)構(gòu)元的模糊數(shù)空間并不是完備的度量空間,但是這一理論給出的模糊數(shù)值函數(shù)有較好的解析式表達(dá),所對(duì)應(yīng)的模糊運(yùn)算也相對(duì)簡(jiǎn)單[13]。基于以上考慮,本文首先給出了基于結(jié)構(gòu)元的模糊值Riemann-Liouville分?jǐn)?shù)階積分的定義,討論了其性質(zhì)。其次，借助于廣義模糊微分研究了模糊值Caputo分?jǐn)?shù)階微分，給出了其存在的充分條件，并討論了模糊值Caputo分?jǐn)?shù)階微分和模糊值Riemann-Liouville分?jǐn)?shù)階積分之間的關(guān)系。最后，討論了常系數(shù)一階線性模糊值Caputo分?jǐn)?shù)階微分方程，并借助于實(shí)值Laplace變換給出了其解的具體形式。

1 定義及說明

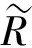
數(shù)乘運(yùn)算u+ν,ku分別定義為[3]:

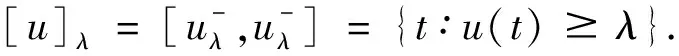
定義1[12～13]設(shè)A是有限模糊數(shù), 若存在一個(gè)模糊結(jié)構(gòu)元E和有限實(shí)數(shù)a∈,r∈+使得A=a+rE,則稱A是模糊結(jié)構(gòu)元E線性生成的模糊數(shù)。由結(jié)構(gòu)元E線性生成的模糊數(shù)全體記作

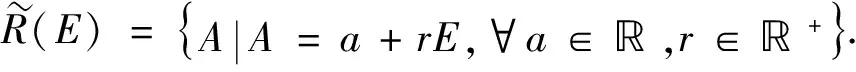
下文中所討論的模糊值函數(shù)均滿足F(x)∈N(Ef).

定義2[15]設(shè)F(t)∈N(Ef). 若

或

成立,則稱F(t)在t=t0處廣義可微。特別地,若F(t)滿足1)式,則稱F(t)是gH1可微; 若F(t)滿足2)式,則稱F(t)是gH2可微。

引理1[15]設(shè)F(t)∈N(Ef),F(t)=f(t)+w(t)E, 其中f(t),w(t)是連續(xù)的實(shí)值函數(shù)。

1)若w(t)單調(diào)遞增,則F(t)是gH1可微,且F′(t)=f′(t)+w′(t)E;

2)若w(t)單調(diào)遞減,則F(t)是gH2可微,且F′(t)=f′(t)+(-1)w′(t)E.

2 基于結(jié)構(gòu)元的模糊值Caputo分?jǐn)?shù)階微分

首先介紹實(shí)值Riemann-Liouville分?jǐn)?shù)階積分。若實(shí)值函數(shù)φ∈L[a,b],將φ的α∈[0,1]階Riemann-Liouville分?jǐn)?shù)階積分定義為[14]：

與上述定義類似,下面給出模糊值Riemann-Liouville分?jǐn)?shù)階積分的定義:

定義3 對(duì)任意F(t)∈N(Ef),記F的α∈[0, 1]階模糊值Riemann-Liouville分?jǐn)?shù)階積分為:

定理1 設(shè)F(t),G(t)∈N(Ef),且F(t)=f(t)+w(t)E,對(duì)任意a≤t≤b,α∈[0,1]有

證明 不失一般性,只證明1)式. 對(duì)任意a≤t≤b,α∈[0,1],由定義3可得

推論1 設(shè)F(t)∈N(Ef),F(t)=f(t)+w(t)E, 對(duì)任意a≤t≤b,α∈[0,1]有

例1 設(shè)F(t)=t+et·E,則由定理1可得

進(jìn)一步有

現(xiàn)在介紹實(shí)值Caputo分?jǐn)?shù)階微分. 若實(shí)值函數(shù)φ∈L[a,b],將φ的α∈[0,1]階Caputo分?jǐn)?shù)階微分定義為[14]:

與上述定義類似,下面給出模糊值Caputo分?jǐn)?shù)階微分的定義:

定義4 對(duì)任意F(t)∈N(Ef),記F的α∈[0,1]階模糊值Caputo分?jǐn)?shù)階微分為:

簡(jiǎn)稱gH-Caputo分?jǐn)?shù)階微分, 其中F′(t)表示廣義可微. 特別地,若F′(t)表示gH1可微,則稱之為gH1-Caputo分?jǐn)?shù)階微分;若F′(t)表示gH2可微,稱之為gH2-Caputo分?jǐn)?shù)階微分.

定理2 設(shè)F(t)∈N(Ef),F(t)=f(t)+w(t)E, 則對(duì)任意a≤t≤b,α∈[0,1]有

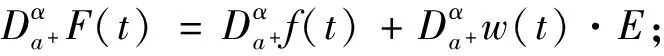
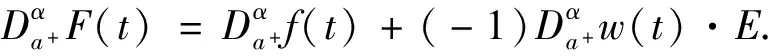
證明 1)若w(t)單調(diào)遞增,由引理1得F′(t)=f′(t)+w′(t)E,對(duì)任意a≤t≤b,α∈[0,1]有

2)若w(t)單調(diào)遞增,由引理1得F′(t)=f′(t)+(-1)w′(t)E,對(duì)任意a≤t≤b,α∈[0,1]有

推論2 設(shè)F(t)∈N(Ef),F(t)=f(t)+w(t)E, 對(duì)任意a≤t≤b,α∈[0,1]有

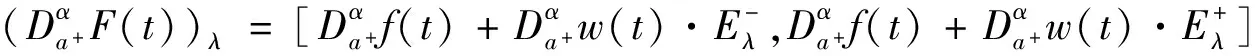
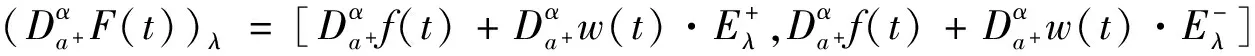
定理3 設(shè)F(t),G(t)是由同一模糊結(jié)構(gòu)元E生成的模糊值函數(shù), 記F(t)=f(t)+w1(t)E,G(t)=g(t)+w2(t)E, 下列事實(shí)成立:

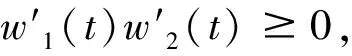
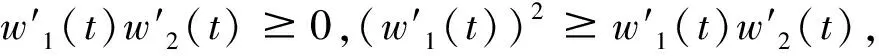
同理可得(F+G)(t)是gH1可微,且有

(F+G)′(t)=(f(t)+g(t))′+(w1(t)+w2(t))′E

=F′(t)+G′(t)

根據(jù)定理1可得

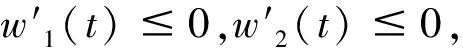
同理可得(F+G)(t)是gH2可微,且有

(F+G)′(t)=(f(t)+g(t))′+(-1)(w1(t)+w2(t))′E

=F′(t)+G′(t)

根據(jù)定理1可得

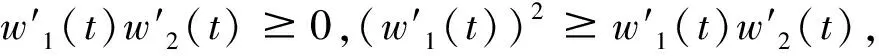
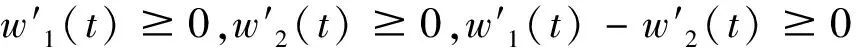
(F-G)′(t)=(f(t)-g(t))′+(w1(t)-w2(t))′E

=F′(t)-G′(t)

進(jìn)而有

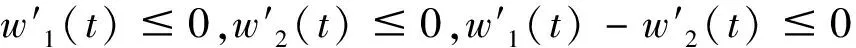
(F-G)′(t)=(f(t)-g(t))′+(-1)(w1(t)-w2(t))′E

=F′(t)-G′(t)

進(jìn)而有

例2 設(shè)F(t)=t+et·E,則由定理1可得

進(jìn)一步有

例3 1)設(shè)F(t)=t+t3·E，則由定理2可得

從而有

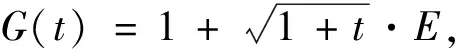
從而有

2)由定理3可得

定理4 設(shè)F(t)∈N(Ef),F(t)=f(t)+w(t)E,F(t)廣義可微,對(duì)任意a≤t≤b,α∈[0,1],如下事實(shí)成立:

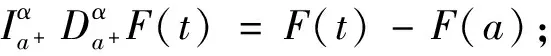
證明 不失一般性,只證1)式。若w(t)單調(diào)遞增,由定理2可得

進(jìn)而根據(jù)定理1有

=f(t)-f(a)+(w(t)-w(a))E

=F(t)-F(a)

定理5 設(shè)F(t)∈N(Ef),F(t)=f(t)+w(t)E,F(t)廣義可微,則對(duì)任意a≤t≤b,α∈[0,1],如下事實(shí)成立：

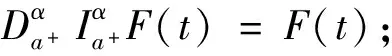
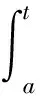
證明 不失一般性,只證1)式.因?yàn)閣(t)單調(diào)遞增,由文獻(xiàn)[9]中引理1知

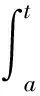
=f(t)+w(t)·E

=F(t)

3 模糊值Caputo分?jǐn)?shù)階微分方程

下面討論常系數(shù)一階線性模糊值Caputo分?jǐn)?shù)階微分方程,

(*)

其中Y(t)=y(t)+w(t)E,F(t)+f(t)+w0(t)E.

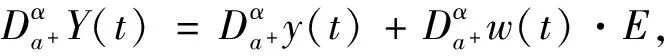
也即

從而可得

其中L[f(t)],L-1[f(t)]分別表示Laplace變換和Laplace逆變換。

定理6 設(shè)Y(t)=y(t)+w(t)E,其中y(t),w(t)是連續(xù)的實(shí)值函數(shù),若w(t)單調(diào)遞增,則Y(t)是gH1-Caputo可微,且Y(t)是(*)式的解,其中

也即

解得

定理7 設(shè)Y(t)=y(t)+w(t)E,其中y(t),w(t)是連續(xù)的實(shí)值函數(shù),若w(t)非負(fù)且單調(diào)遞減,則Y(t)是gH2-Caputo可微,且Y(t)是(*)式的解,其中

當(dāng)m≤0時(shí),(*)式解的討論與上面類似,文中省略。

4 結(jié)論

本文首先給出了基于結(jié)構(gòu)元的模糊值Riemann-Liouville分?jǐn)?shù)階積分的定義，討論了其性質(zhì)。其次，借助于廣義模糊微分研究了模糊值Caputo分?jǐn)?shù)階微分,給出了其存在的充分條件,并討論了模糊值Caputo分?jǐn)?shù)階微分和模糊值Riemann-Liouville分?jǐn)?shù)階積分之間的關(guān)系。最后，討論了常系數(shù)一階線性模糊值Caputo分?jǐn)?shù)階微分方程，并借助于實(shí)值Laplace變換給出了其解的具體形式。