混合風電場接入含固定串補系統的次同步振蕩特性分析

王俊茜,賈 祺,劉 侃,翟文超,王 健

（1.東北電力大學 現代電力系統仿真控制與綠色電能新技術教育部重點實驗室，吉林 吉林 132012；2.國網遼寧電力科學研究院，遼寧 沈陽 110006）

0 引言

近年，由于風電的廣泛接入，電力系統次同步振蕩（Sub-SynchronousOscillation，SSO）事故頻發[1]。2009年10月，美國德州某風電場雙饋風電場（Doubly-Fed Induction Generator，DFIG）與串補電網間發生20Hz左右的次同步諧振事故，造成大量風電場撬棒電路損壞和異常脫網[2]。2012年12月，我國沽源地區風電場也出現了由串補電容導致風機6～8Hz振蕩，嚴重地威脅了電網及風電場安全運行[3]。

國內外學者基于特征值分析、阻抗分析等方法，對DFIG風電場并網引發的SSO現象開展了研究，分析了DFIG風電場運行風速、串補度以及控制參數等因素對其振蕩特性的影響規律。研究結果表明，DFIG風電場接入含固定串補系統發生的SSO現象是控制系統參與的感應發電機效應[4]，[5]。振蕩特性主要受運行風速、串補度及轉子電流內環控制參數的影響，且隨著DFIG風電場運行風速的增加、控制參數及串補度的減小，系統運行穩定性增加[6]，[7]。但實際風電場通常包含直驅 風 電 場 （Direct-Drive Permanent Magnet SynchronousGenerator，PMSG）。文獻[8]圍繞沽源地區風電場次同步諧振現象展開研究，針對風電場控制參數固定的場景，基于阻抗分析法研究混合風電場中PMSG對次同步諧振的影響，結果表明，PMSG對系統次同步諧振存在影響，但并未分析風電場運行風速、控制參數等因素對振蕩的影響演變規律。文獻[9]基于特征值法進一步研究混合風電場SSO振蕩特點，研究表明風電場中DFIG和PMSG風機比例、串補水平會對SSO產生影響，但未從機理上解釋風電場接入影響系統穩定性的原因。

在PMSG風電場中，由于背靠背變流器的存在，使得永磁同步發電機與電網解耦。文獻[10]基于時頻分析方法，指出PMSG風電場不存在感應發電機效應。文獻[11]以華北沽源系統的實際錄波數據為基礎，驗證了PMSG風電場接入固定串補系統不會發生振蕩；但新疆哈密地區發生PMSG風電場次同步振蕩事故，須重新評估PMSG風電場的動態特性及影響因素。文獻[12]通過電磁暫態仿真、阻抗模型等方法指出PMSG風電場的動態特性與變流器控制系統強相關，且不同控制參數下，PMSG對外呈現的容抗、感抗以及電阻特性可能不一致。此外，FACTS技術推動了SSO抑制方面的研究工作發展，目前已有的抑制SSO現象的方法多為在STATOM，SVC上增加附加勵磁阻尼控制環節[13]，[14]。

本文以PMSG，DFIG風電場并聯接入含固定串補的系統為對象，研究了PMSG風電場對于DFIG風電場的SSO抑制作用。建立包含兩種機型的混合風電場線性化模型，分析風機占比、控制參數、運行風速對系統運行性的影響。基于混合風電場動態阻抗模型進一步揭示系統次同步振蕩機理。在EMTDC/PSCAD中搭建時域仿真模型，仿真結果驗證了理論分析的正確性與可行性。

1 混合風電場建模

混合風電場拓撲結構如圖1所示。DFIG風電場和PMSG風電場并聯，經輸電線路連接至電網，圖中Lg，Cg分別為輸電線路電感和串補電容。為了簡化分析，假設風電場各臺風機的運行狀態是相同的，本文模型中的風電場采用單機倍乘的建模方式。

圖1 混合風電場系統結構圖Fig.1 Structure diagram of hybrid-based wind farm integration

1.1 DFIG風電場模型

DFIG拓撲結構及其控制系統如圖2所示。

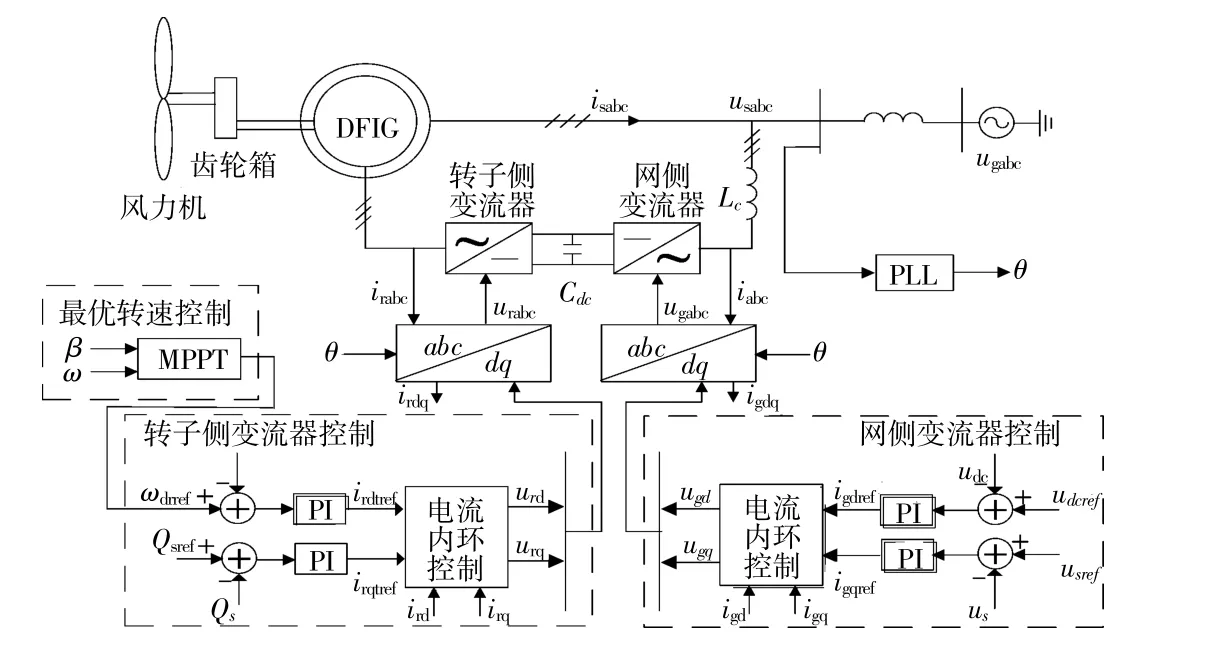
圖2 DFIG風電場拓撲結構及控制策略圖Fig.2 The topology and control system of DFIG based wind farm

DFIG主要由風力機、異步電機、轉子變流器、網側變流器4部分構成。轉子變流器與網側變流器通常采用電壓矢量定向控制策略。為了實現風能的最大化利用，轉子變流器通常采用MPPT控制策略；網側變流器通常以直流電壓與無功功率為控制目標。圖中：ω，β分別為風機轉速和槳距角；ωdr，ωdrref分別為轉子轉速及其參考值；Qs，Qsref分別為定子側無功功率及其參考值；irdq，irdqref分別為dq坐標系轉子側變流器電流實際值及其參考值；irabc為abc坐標系轉子側變流器電流實際值；isdq，isabc為定子輸出電流；urdq，urabc為轉子側變流器調制電壓；usabc為abc坐標系下定子電壓；us，usref分別為定子電壓幅值及其參考值；udc，udcref分別為直流電容電壓及其參考值；igdq，igdqref分別為dq坐標系下網側變流器電流實際值及其參考值；igabc，ugabc分別為abc坐標系下網側變流器電流實際值和調制電壓；Cdc為直流電容；Lc為連接電抗；θ為鎖相環輸出相位。

在平衡點處線性化后，DFIG的數學模型為[15]

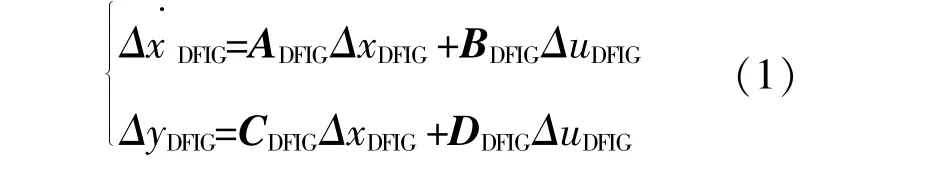
式中：ADFIG，BDFIG，CDFIG，DDFIG分別為DFIG風電場的狀態矩陣、輸入矩陣和輸出矩陣。狀態變量增量ΔxDFIG=[Δωdr，Δisd，Δisq，Δird，Δirq，Δigd，Δigq，Δudc，Δx1～Δx8]，其中Δx1～Δx8為控制系統狀態變量；ΔuDFIG=[Δusd，Δusq]T，ΔyDFIG=[Δisd，Δisq]T分別為輸入、輸出變量。

1.2 PMSG風電場模型

PMSG拓撲結構如圖3所示。PMSG主要由風力機、永磁同步發電機、四象限變流器、濾波電路等構成。圖中，機側變流器采用定子電流ipsd=0的dq解耦控制策略，將永磁同步機轉子角速度ωr與給角速度參考值ωrref比較，差值經PI環輸出即為q軸電流參考值，dq軸電流經電流內環PI調節，形成變流器輸出電壓，經PWM調制，輸出脈沖信號控制機側變流器。網側變流器采用電網電壓矢量定向控制，將直流側電壓Udc與給定母線電壓參考值Udcref比較，差值經PI環輸出即為d軸電流參考值，dq軸電流經電流內環PI調節，形成變流器輸出電壓，經PWM調制，輸出脈沖信號控制網側變流器。

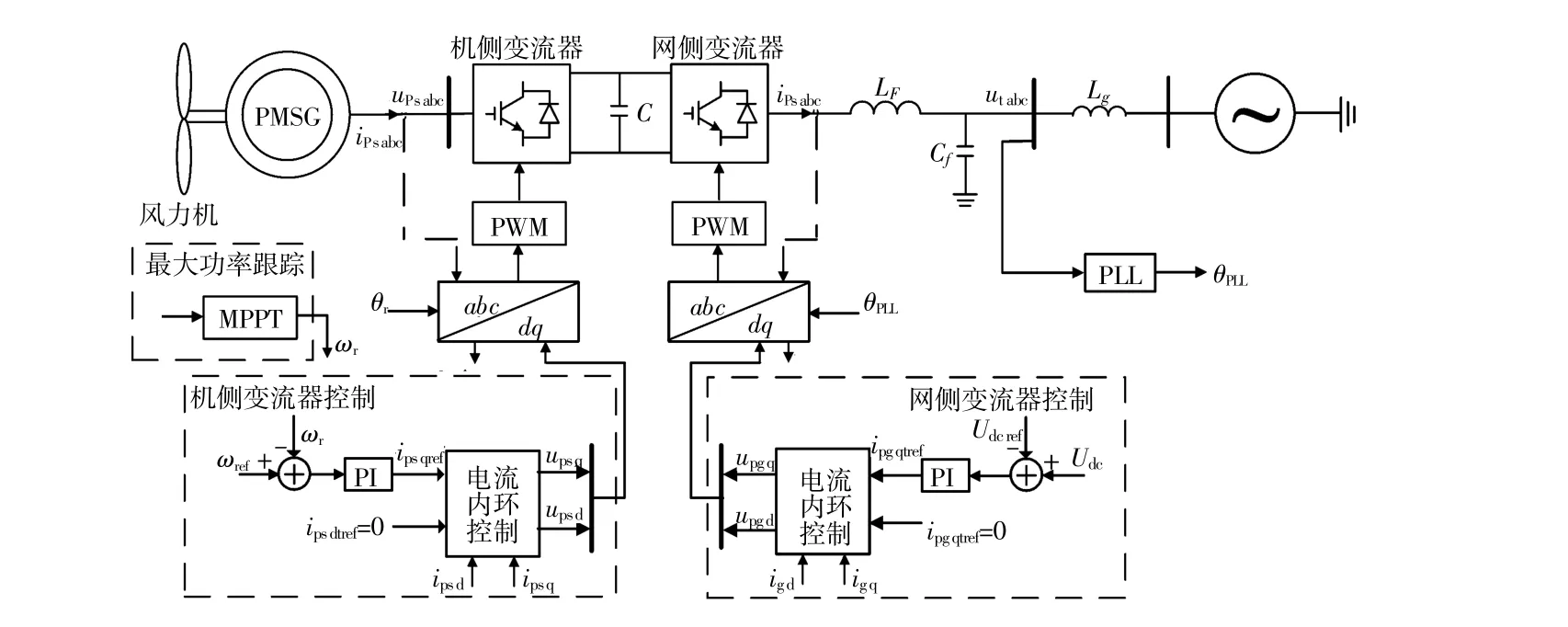
圖3 PMSG風電場拓撲結構及控制策略圖Fig.3 The topology and control system of PMSG based wind farm

圖3中：v為風速；Lf，Cf分別為網側變流器濾波電感及濾波電容；Lg為網側電感；utabc為并網點電壓實際值；ipsdq，ipsabc為定子繞組電流實際值；ipsdqref為定子繞組電流參考值；upsdq，upsabc為定子繞組電壓；upgdq為網側變流器輸出調制電壓；ipgdq，ipgdqref分別為網側變流器輸出電流實際值及其參考值；Udc，Udcref分別為直流電壓實際值及其參考值；θr為轉子側輸出相位；θPLL為鎖相環輸出相位。ωr，ωrref分別為永磁同步加轉子轉速及其參考值。

在平衡點處線性化后，得到PMSG的數學模型為[16]

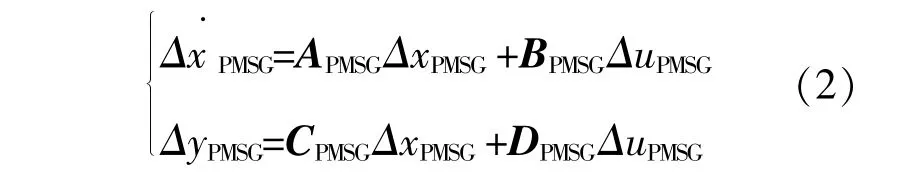
式中：APMSG，BPMSG，CPMSG，DPMSG分別為PMSG風電場的狀態矩陣、輸入矩陣和輸出矩陣。狀態變量增量ΔxPMSG=[Δωr， Δipsd， Δipsq， Δipgd， Δipgq，ΔUdc，Δxp1～Δxp8]；Δxp1～Δxp8為 控 制 系 統 狀 態 變 量；ΔuPMSG=[Δupsd，Δupsq]T，ΔyPMSG=[Δipsd，Δipsq]T分別為輸入、輸出變量。

2 特征值分析

基于混合風電場線性化模型，分析風電場占比、PMSG風電場控制參數、運行風速等因素變化對系統振蕩特性的影響。

2.1 風電場占比變化對系統穩定性的影響

DFIG風電場風速為4.5m/s，DFIG控制參數為（0.03，0.05）；PMSG風電場風速為4m/s，PMSG直流電壓環控制參數為（2，1000）、電流內環控制參數為（0.23，50）；當PMSG風電場占比由0～50%變化（風機總并聯臺數為2 000臺）、串補度由5%～30%變化時，DFIG和PMSG風電場并聯接入含固定串補系統的次同步振蕩模式變化軌跡如圖4所示。

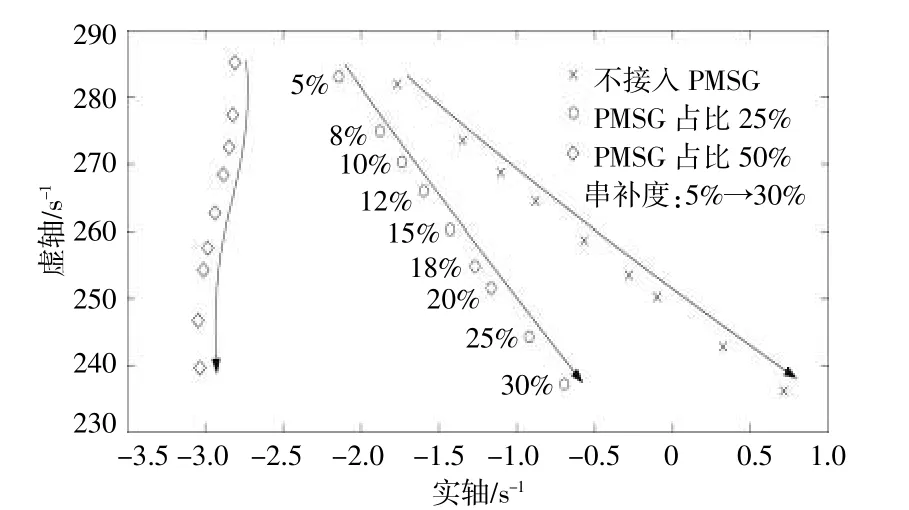
圖4 定輸送容量下次同步振蕩模式變化軌跡Fig.4 The variation trajectory of SSOmode under fixed transmission capacity

由圖4可知，隨著串補度的增加，次同步振蕩模式的阻尼逐漸減小，系統穩定性降低，且振蕩頻率逐漸減小；相同串補度下，隨著PMSG占比的增加，系統穩定性增強。

2.2 PMSG風電場控制參數變化對系統穩定性的影響

DFIG風電場風速為4.5 m/s，并網臺數為1 000臺，DFIG控制參數為（0.03，0.05）；PMSG風電場風速為4m/s，PMSG直流電壓環控制參數（2，1 000），并網臺數1 000臺；當PMSG風電場電流內環控制參數在0.1～0.3變化、串補度在5%～30%變化時，DFIG和PMSG風電場并聯接入含固定串補系統的次同步振蕩模式變化軌跡，如圖5所示。由圖5可知，相同串補度下，隨著PMSG風電場電流內環控制增加，次同步振蕩模式的阻尼變化規律不明顯。

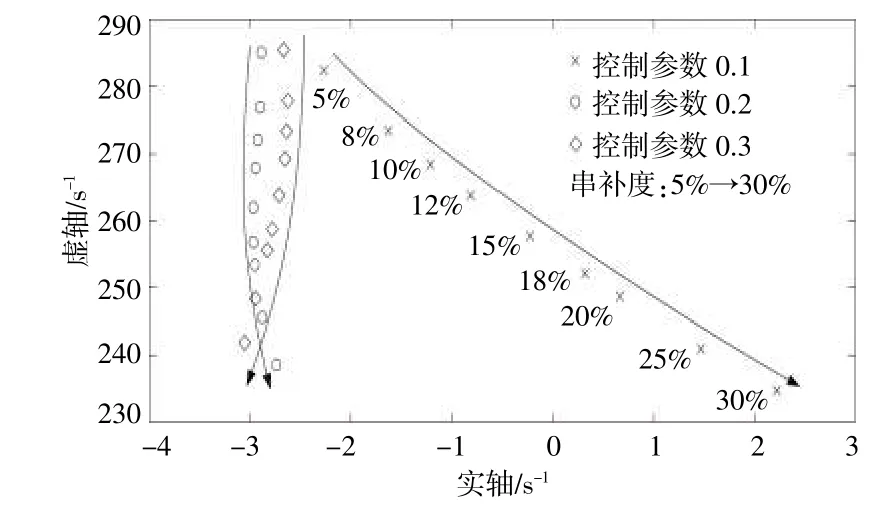
圖5 定控制參數下次同步振蕩模式變化軌跡Fig.5 The variation trajectory of SSOmode under fixed control parameter

2.3 PMSG風電場運行風速對系統穩定性的影響

DFIG風電場風速為4.5 m/s，并網臺數為1 000臺，DFIG控制參數為（0.03，0.05）；PMSG直流電壓環控制參數（2，1 000）、電流內環控制參數（0.23，50），并網臺數為1 000臺；當PMSG風電場風速由4～6m/s變化、串補度由5%～30%變化時，DFIG和PMSG風電場并聯接入含固定串補系統的次同步振蕩模式變化軌跡如圖6所示。

圖6 定運行風速下次同步振蕩模式變化軌跡Fig.6 The variation trajectory of SSOmode under fixed operating wind speed

由圖6可知：隨著串補度的增加，次同步振蕩模式的阻尼呈現減小、增加、再減小的非線性變化趨勢，且振蕩頻率逐漸減小；相同串補度下，隨著PMSG風電場風速增加，系統穩定性降低。

3 PMSG風電場阻抗特性及對系統阻抗特性的影響

為進一步揭示混合風電場振蕩機理，本文從風電場的動態阻抗特性角度開展研究，DFIG，PMSG風電場并聯系統的動態阻抗（正序）表達式分別為

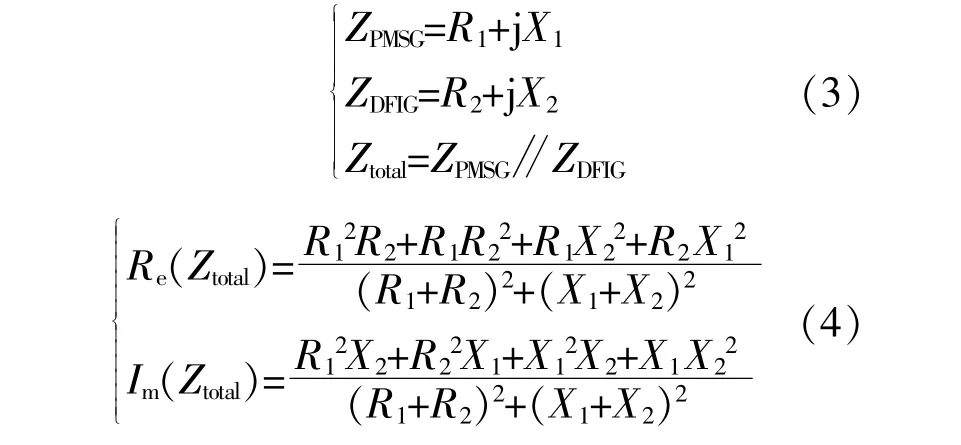
式中：ZPMSG為PMSG風電場阻抗；R1，X1分別為其等效電阻與等效電抗；ZDFIG為DFIG風電場阻抗；R2，X2分別為DFIG等效電阻與等效電抗；Ztotal為并聯系統總阻抗。

由式（3），（4）可知，PMSG風電場阻抗和DFIG風電場阻抗，共同決定風電場并聯系統總電阻的正負值；由于次同步頻段下DFIG風電場負電阻特征凸顯，系統總電阻Re（Ztotal）的第一項×R2和第四項R2×均＜0，若想Re（Ztotal）＞0，則須要選擇PMSG風電場合適的控制參數、運行風速來保證R1＞0；在滿足上述條件下，R1取值偏小些，可能越有利于系統穩定。

本文利用頻率掃描法，研究風電場占比、PMSG風電場控制參數、運行風速變化對DFIG次同步振蕩特性的影響規律。具體掃頻流程如下：①在穩定運行狀態下的風電場端口注入一個頻率連續變化的三相電壓擾動信號；②測量風電場端口的輸出電壓Vmabc和輸出電流iabc；③對輸出電壓和輸出電流曲線進行傅立葉分解，基于Z（f）=Vm（f）/i（f），計算次同步頻段下風電場動態阻抗。

3.1 風電場不同占比對次同步振蕩特性的影響

DFIG風電場風速為4.5m/s，DFIG控制參數為（0.03，0.05）；PMSG風電場風速為4m/s，PMSG直流電壓環控制參數為（2，1 000）、電流內環控制參數為（0.23，50），當PMSG風電場占比為25%～50%時，PMSG風電場的動態阻抗如圖7所示。

由圖7可知：1～38 Hz頻段內，PMSG風電場的動態電阻隨頻率增加而減小；38～40 Hz頻段內，動態電阻隨頻率增加而增加；40～45 Hz頻段內，動態電阻隨頻率增加而減小；1～39 Hz頻段內，PMSG風電場的動態電抗隨頻率先增加后減小；39～41Hz頻段內，動態電抗隨頻率增加而增加；41～45Hz頻段內，動態電抗隨頻率增加而減小。考慮到DFIG風電場振蕩場景中的振蕩頻率在2～20Hz（abc坐標系），隨著PMSG風電場占比增加，PMSG風電場的動態電阻逐漸減小（以下分析中也重點關注2～20Hz風電場動態電阻特性）。

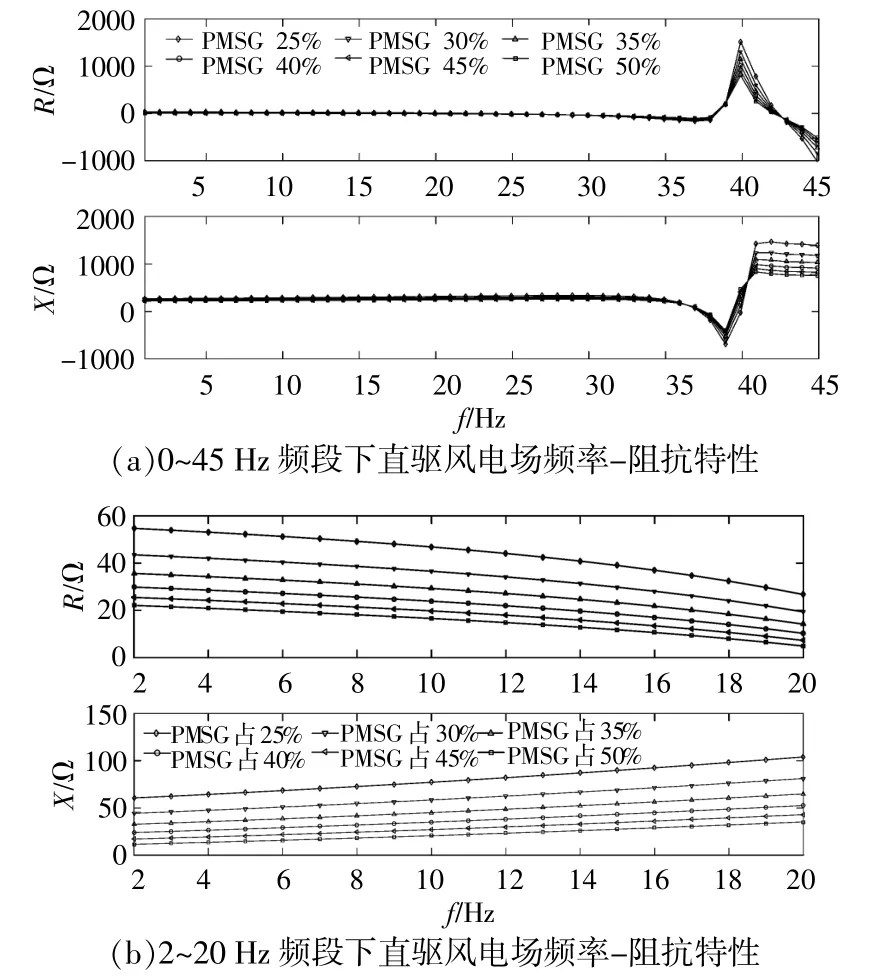
圖7 不同占比下直驅風電場頻率-阻抗特性Fig.7 The frequency-impedance characteristics of PMSG based wind farm under different proportions

保證風電場輸送容量不變，DFIG風電場風速為4.5m/s、PMSG風電場運行條件如上所述，當PMSG風電場占比為25%～50%時，風電場并聯系統的動態阻抗如圖8所示。

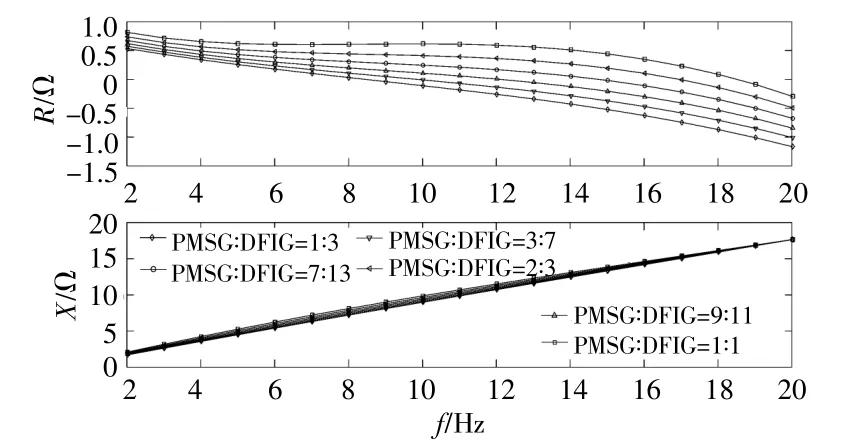
圖8 不同占比下系統頻率-阻抗特性Fig.8 The frequency-impedance characteristics of the system under different proportions

由圖8可知，2～20Hz頻段內，風電場并聯系統的動態電阻隨PMSG風電場占比的增加而增大，有利于系統穩定運行。

3.2 不同控制參數對次同步振蕩特性的影響

PMSG風電場風速為4 m/s、并網臺數為1000臺、直流電壓環控制參數（2，1000），當電流內環控制參數由0.1～0.35變化時，PMSG風電場的動態阻抗如圖9所示。

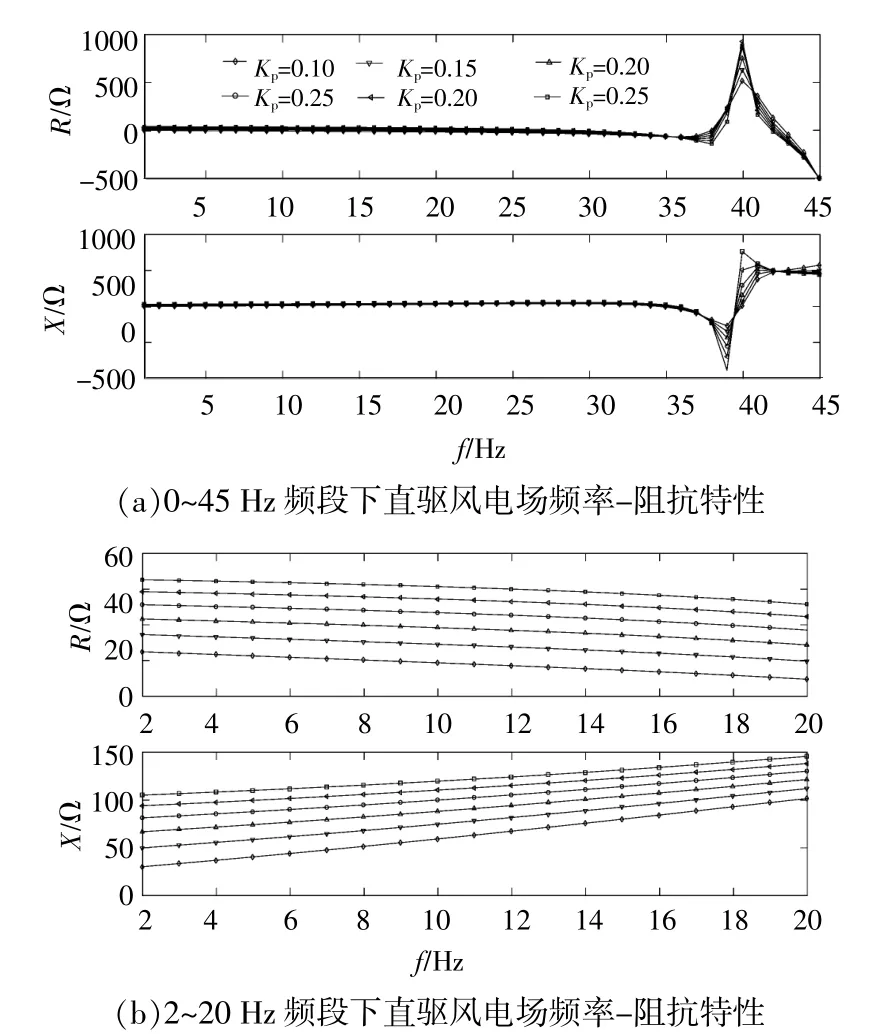
圖9 不同控制參數下直驅風電場頻率-阻抗特性Fig.9 The frequency-impedance characteristics of PMSG based wind farm under different control parameters

由圖9可知：1～45Hz頻段內，PMSG風電場的動態阻抗變化趨勢與圖5一致；隨著PMSG風電場控制參數增加，PMSG風電場的動態電阻逐漸增加。

DFIG風速為4.5m/s、并網臺數為1 000臺、PMSG風電場運行條件如上所述，當PMSG風電場電流內環控制參數由0.1～0.35變化時，風電場并聯系統的動態阻抗如圖10所示。由圖10可知：2～12Hz頻段內，風電場并聯系統的動態電阻隨控制參數變化規律不明顯；12～20 Hz頻段內，風電場并聯系統的動態電阻隨控制參數增加而變大，該頻段下控制參數增加有利于系統穩定。

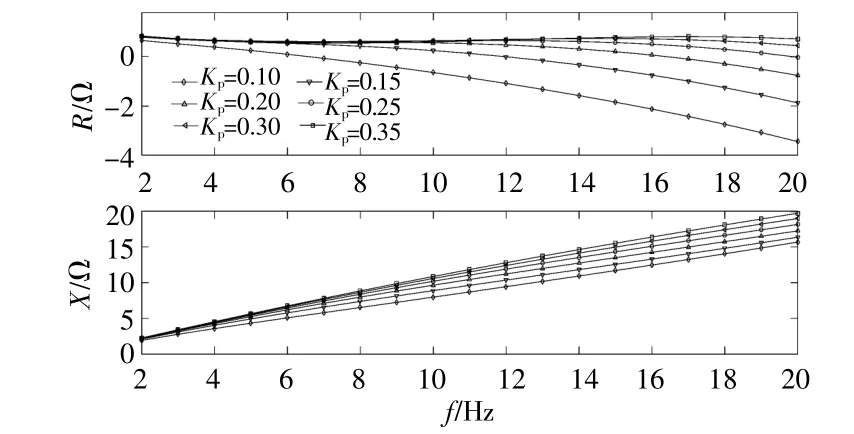
圖10 不同控制參數下系統頻率-阻抗特性Fig.10 The frequency-impedance characteristics of the system under different control parameters

3.3 不同運行風速對次同步振蕩特性的影響

PMSG風電場并網臺數為1 000臺、直流電壓環控制參數為（2，1 000）、電流內環控制參數為（0.23，50），當風速由3.5～6m/s變化時，PMSG風電場的動態阻抗如圖11所示。

圖11 不同運行風速下直驅風電場頻率-阻抗特性Fig.11 The frequency-impedance characteristics of PMSG based wind farm under differentoperating wind speeds

由圖11可知：1～45Hz頻段內，PMSG風電場的動態阻抗變化趨勢與圖5一致；隨著PMSG風電場運行風速增加，PMSG風電場的動態電阻變化不顯著。

DFIG風電場風速為4.5 m/s、并網臺數為1 000臺、PMSG風電場運行條件如上所述，當PMSG風電場運行風速由3.5～6m/s變化時，風電場并聯系統的動態阻抗如圖12所示。

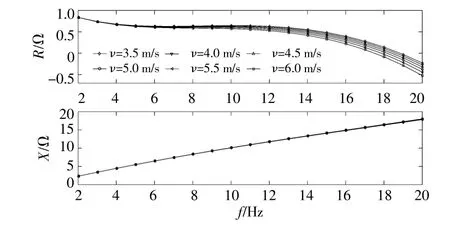
圖12 不同運行風速下系統頻率-阻抗特性Fig.12 The frequency-impedance characteristics of the system under differentoperatingwind speeds

由圖12可知，2～20Hz頻段內，風電場并聯系統的動態電阻隨運行風速增加而減小，降低系統的運行穩定性。

4 仿真及結果分析

為驗證上述分析的正確性，本節進行時域仿真分析，在EMTDC/PSCAD中搭建了圖1所示的仿真模型。當串補度為25%、風電場輸送容量恒定；DFIG風電場風速為4.5m/s、DFIG控制參數為（0.03，0.05）；PMSG風電場風速為4m/s，PMSG直流電壓環控制參數為（2，1 000）、電流內環控制參數為（0.23，50）；t=6 s時投入串補電容，不同風電場占比條件下系統次同步振蕩特性波形，如圖13所示。

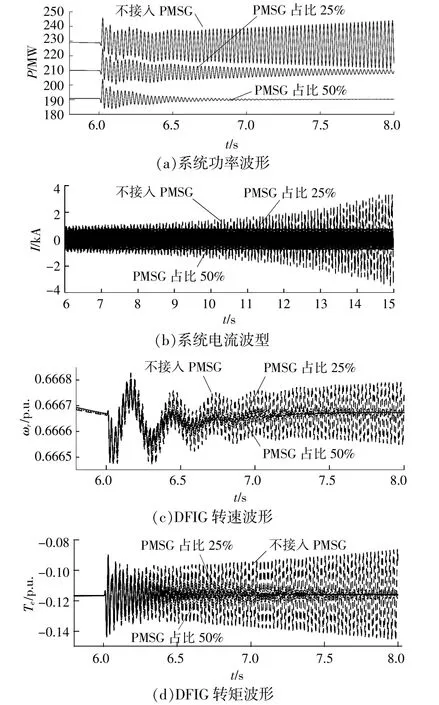
圖13 不同占比下系統次同步振蕩特性波形Fig.13 The SSO characteristic waveform of the system under different proportions

由圖13可知，隨著PMSG風電場占比的增加，系統穩定性增加，與理論分析結果一致。

當串補度為25%、DFIG風電場風速為4.5 m/s、并網臺數為1 000臺、DFIG控制參數為（0.03，0.05）；PMSG風電場風速為4m/s、并網臺數1 000臺、直流電壓環控制參數為（2，1 000）；t=6 s時投入串補電容，不同PMSG風電場電流內環控制參數下系統次同步振蕩特性波形如圖14所示。

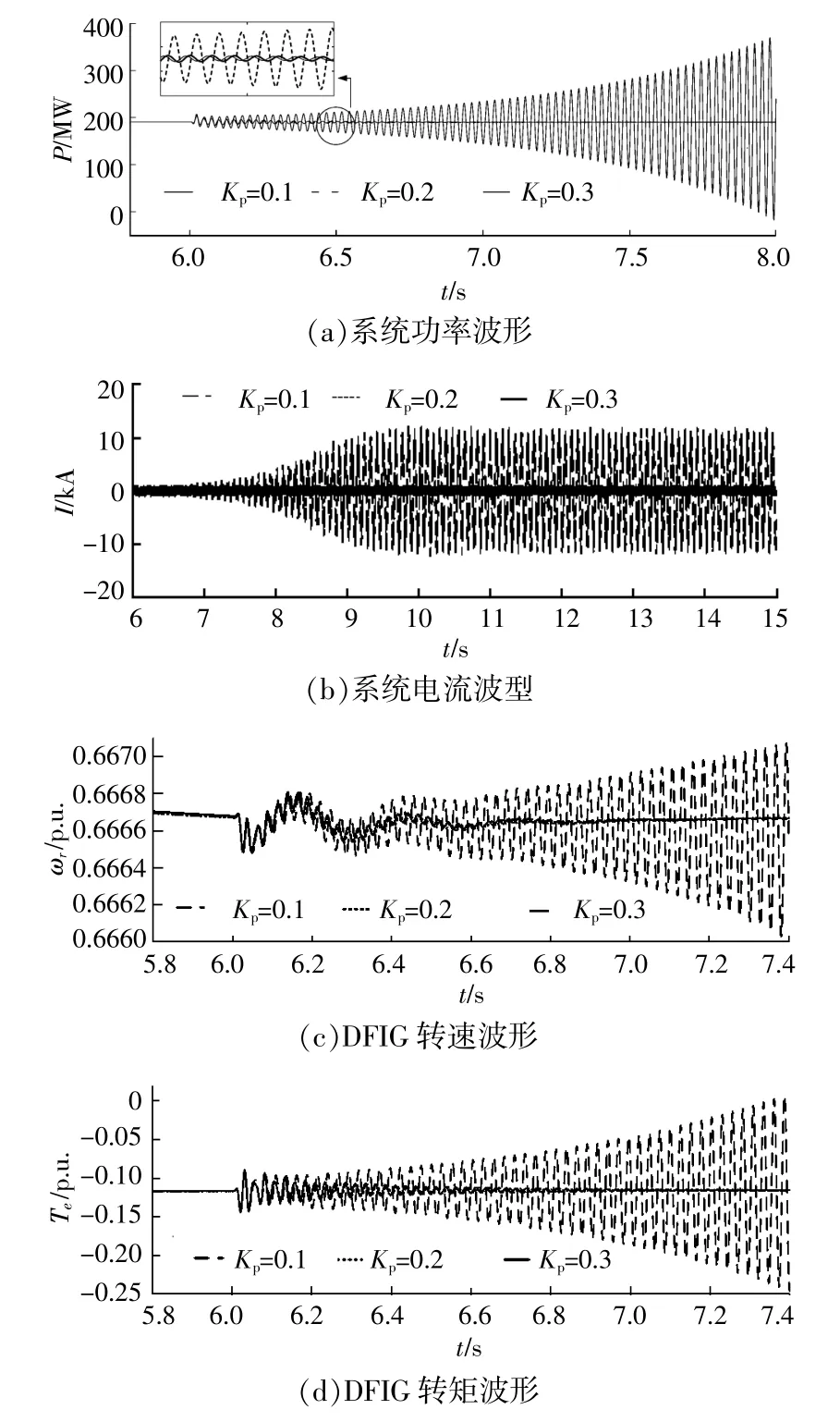
圖14 不同控制參數下系統次同步振蕩特性波形Fig.14 The SSO characteristic waveform of the system under different control parameters

由圖14可知，隨著PMSG風電場控制參數增加，系統穩定性增加，但變化規律不明顯。

當串補度為25%、DFIG風電場風速為4.5 m/s、并網臺數為1 000臺、DFIG控制參數為（0.03，0.05）；PMSG風電場并網臺數1 000臺、直流電壓環控制參數為（2，1000）、電流內環控制參數為（0.23，50）；t=6 s時投入串補電容，不同PMSG風電場運行風速下系統次同步振蕩特性波形如圖15所示。

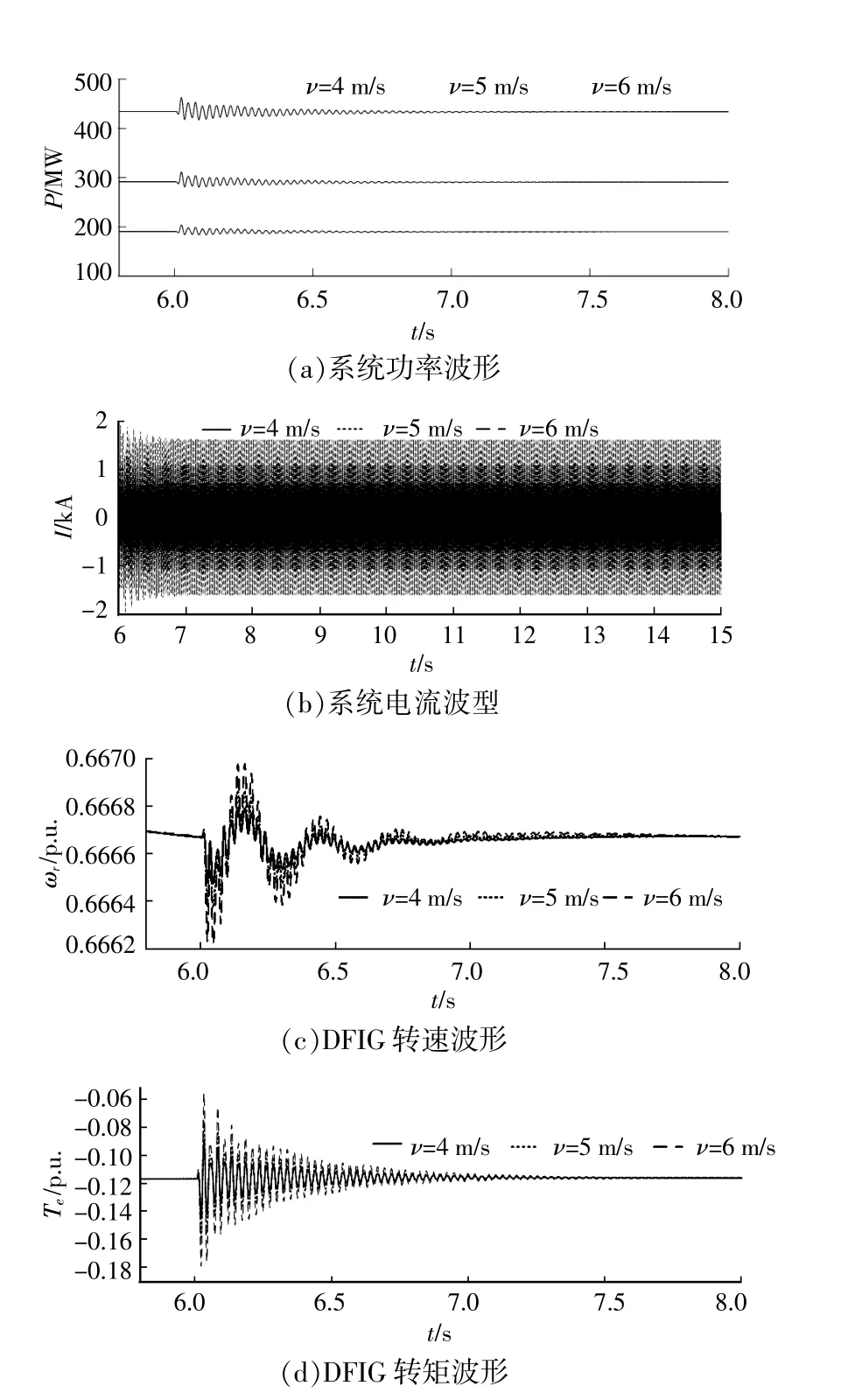
圖15 不同運行風速下系統次同步振蕩特性波形Fig.15 The SSO characteristic waveform of the system under differentoperating wind speeds

由圖15可知，隨著PMSG風電場運行風速增加，系統穩定性降低，與理論分析結果一致。

5 結論

本文研究了在混合風電場接入固定串補系統中，PMSG對DFIG次同步振蕩問題的影響作用。基于混合風電場線性化模型，對系統進行特征值分析，研究風電場占比、PMSG風電場控制參數、運行風速等因素變化對系統穩定性的影響。研究結果表明：①當PMSG風電場占比變化時（25%～50%），在2～20Hz頻段內，PMSG風電場對外呈現正的阻抗特性，隨著PMSG并網臺數的增加，PMSG風電場的動態電阻減小，風電場并聯系統動態電阻增加，系統運行穩定性增強；②當PMSG風電場電流內環控制參數變化時（0.1～0.35），在2～12Hz頻段內，PMSG風電場對外呈現正的阻抗特性，風電場并聯系統的動態電阻隨控制參數變化規律不明顯；12～20 Hz頻段內，系統的動態電阻隨控制參數增加而變大，有利于系統穩定；③當PMSG風電場運行風速變化時（3.5～6m/s），在2～20Hz頻段內，PMSG風電場對外呈現正的阻抗特性，風電場并聯系統的動態電阻隨運行風速增加而減小，降低系統運行穩定性。