混凝土Ⅰ型裂縫失穩擴展時臨界有效縫長的數值研究

鄭 軼 王向東 劉慶輝

(河海大學 力學與材料學院，南京 211100)

混凝土是由水泥、砂、骨料、水等材料組成的復合材料，在實際工程中混凝土結構難免會出現宏觀裂縫，而其損傷和斷裂特性對工程安全起著關鍵作用.因此，準確把握混凝土的破壞機理，確定合理的混凝土斷裂參數，對評價混凝土結構的穩定性和安全性具有重大意義，對此，國內外學者進行了大量研究工作[1-8].混凝土材料作為一種準脆性材料，其斷裂特性區別于金屬材料，在結構承受荷載作用后，宏觀裂縫尖端存在一個微裂紋區，即斷裂過程區，結構失穩斷裂時，宏觀裂縫已經有了一定的擴展，大量研究表明引入斷裂過程區的影響[9-10]是必要的.

文獻[11]對混凝土裂縫失穩擴展臨界有效裂縫長度進行了研究，即通過實驗和數值模擬的方法對測定的F-δ(荷載-位移)曲線，采用柔度改變法測得有效裂縫縫長，該方法得到的臨界有效縫長，結果是合理的，但是斷裂過程區的存在對裂縫擴展的影響必須從斷裂和損傷力學理論的角度進行研究，一方面使研究結果更具科學理論依據支撐，另一方面考慮損傷對裂縫擴展的影響更符合實際情況.

本文在文獻[11]的基礎上，從斷裂與損傷耦合的角度，推導出計算混凝土Ⅰ型裂縫失穩擴展臨界有效裂縫長度的新方法，并通過數值模擬實驗，對計算結果進行對比分析，進一步計算失穩斷裂韌度，與傳統計算方法和文獻[11]計算方法進行對比，以驗證推導方法的可行性并且說明考慮混凝土宏觀裂縫前端微裂紋區的斷裂與損傷對斷裂韌度的影響是有必要的.

1 基于虛擬裂縫模型和最大拉應變斷裂判據的有效縫長

1.1 虛擬裂縫模型概述

1976年，Hillerborg等[12]在塑性力學模型的基礎上提出了虛擬裂縫模型(FCM).該模型認為宏觀裂縫擴展前，在裂縫前端已出現微裂縫區.在此區域內，材料剛度降低，從而削弱了該區域傳遞應力的能力.但微裂縫區內仍有骨料相連或基體粘結，因此微裂縫區域內傳遞應力能力并未完全喪失，這部分傳遞的應力稱為黏聚力.通過分離式裂縫的表征方法將微裂縫區定義為“虛擬裂縫區”，也叫斷裂過程區(FPZ).

對于Ⅰ型裂縫，斷裂過程區可表示為黏聚力σ與裂縫張開位移w之間的關系，圖1即在斷裂過程區內黏聚力隨著位移逐漸張開而變化的軟化本構關系.

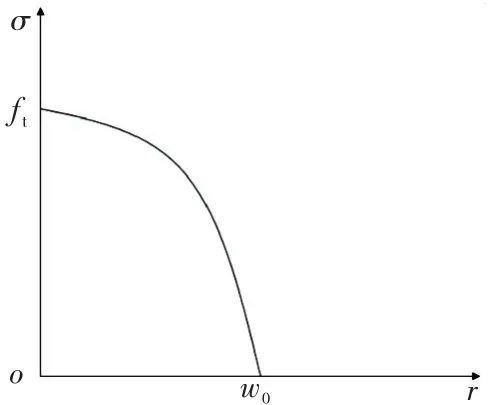
圖1 應力軟化曲線

由圖1可知，當裂縫張開位移w為0時，相應微裂縫區域內的黏聚力等于混凝土抗拉強度;當裂縫張開位移w達到臨界值w0時，對應微裂縫區的黏聚力降為0，此時裂縫區域的虛擬裂縫面不再傳遞應力.

1.2 有效裂縫縫長a c的計算

依據斷裂力學，可得Ⅰ型裂縫尖端應力場公式:

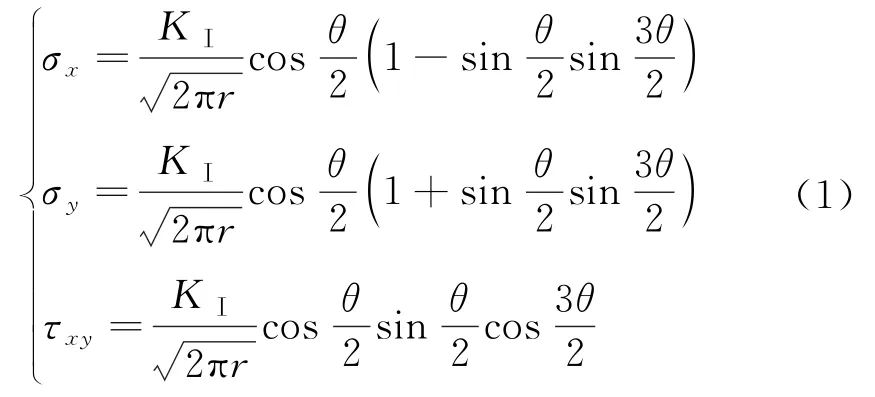
式中:σx、σy、σz為裂縫尖端區域的應力;KⅠ為應力強度因子;r、θ為極坐標.

當混凝土處于失穩擴展臨界狀態時，依據虛擬裂縫模型，在靠近裂縫端部區域內的混凝土沿著裂縫線方向，有一部分微裂縫區域內黏聚力為零，裂縫張開位移w≥w0，因此可將這一區域等效為混凝土的軟化開裂區域，如圖2所示，r0即為軟化區域，該區域的長度即可等效為混凝土臨界有效縫長的增加量Δac.

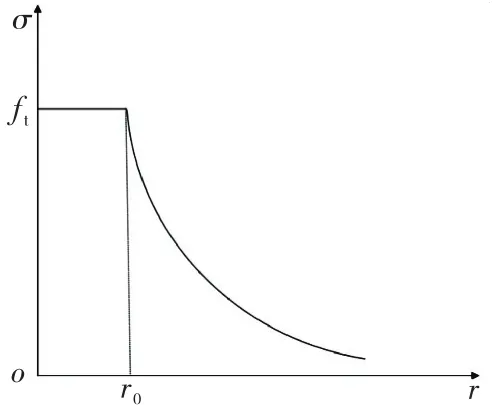
圖2 裂縫尖端區域應力變化情況

由于混凝土是準脆性材料，依據最大拉應變斷裂判據，當裂縫尖端最大拉應變達到極限應變時，裂縫將開始擴展，由胡克定律可得到相應的應力表達式:

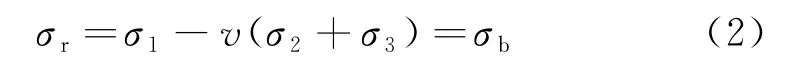
式中:σr為相當應力;σb為極限應力，σ1、σ2、σ3為主應力;v是泊松比.

根據主應力公式，由式(1)可得縫端的主應力為:

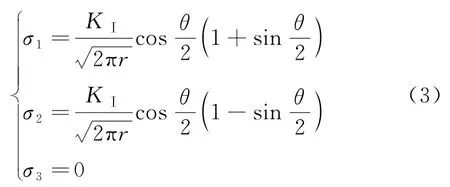
在平面應力狀態下，將式(3)代入式(2)，對于混凝土Ⅰ型裂縫，取混凝土的極限應力σb軸向抗拉強度為ft，并代入(2)，在裂縫線上(θ=0)，則有

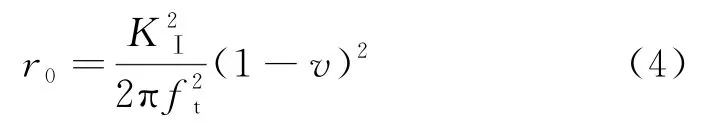
式中:軟化區域r0由于不再傳遞應力，因此可以將其等效成宏觀裂縫有效擴展長度Δac，臨界有效縫長為ac=a0+Δac=a0+r0.

2 基于Loland損傷模型和最大拉應變斷裂判據的有效縫長

2.1 Loland損傷模型

Loland[13]在對混凝土試驗進行研究時發現，當應力即將達到峰值應力前，應力-應變不再是直線關系，這表明當應變小于峰值應變εf時，材料的內部存在著損傷區，當應變大于εf時，材料已經發生嚴重劣化，應力迅速跌落，損傷不斷增大，本文只考慮峰值之前的裂縫尖端混凝土的損傷演化.

常用的混凝土損傷演變方程為:

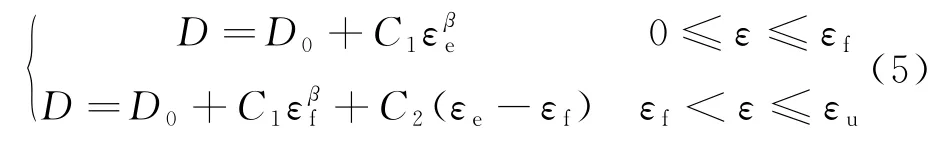
式中:D為損傷;D0為初始損傷;C1、C2和β為材料參數;εf為峰值應力對應的應變;εu為極限應變，ε=εf時，σ=σf，dσ/dε=0，考慮到ε=εu時D=1，得到:

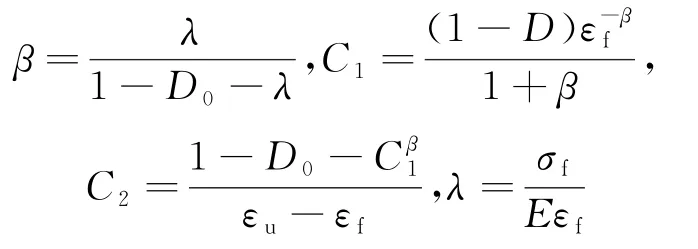
根據文獻[11]取混凝土材料的初始損傷變量D0為0.05，根據文獻中數據計算得到材料參數β=4.4、C1=7×1016、C2=1935，將求出的材料常數代入損傷演化方程(5)可以得到:

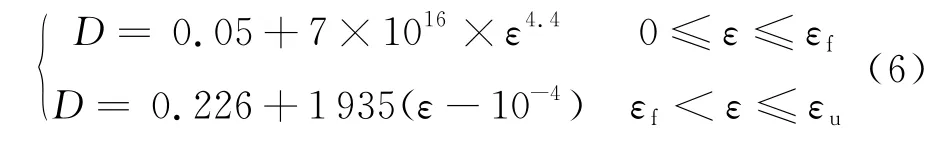
由公式(6)可以得到在峰值前應變與損傷變量之間的關系曲線，如圖3所示，隨著應變的不斷增大，損傷曲線是上升的.

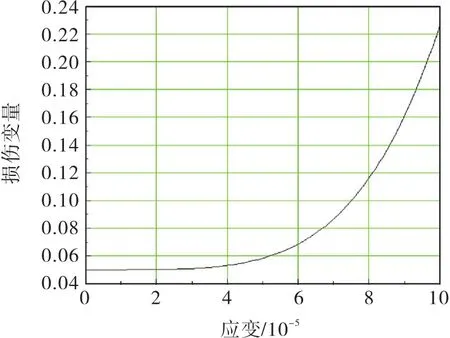
圖3 峰值前的應變與損傷變量之間的關系曲線

2.2 雙D損傷發展判據

文獻[14]中提出了基于損傷和斷裂力學耦合的雙D發展判據:當裂縫尖端的損傷小于起裂損傷Dini時，縫端損傷處于產生階段，微裂縫區形成;當裂縫尖端的損傷介于起裂損傷Dini和失穩損傷Dun之間時，縫端損傷處于穩定積累階段，微裂縫區穩定發展;當裂縫尖端損傷大于Dun時，縫端損傷處于快速失穩發展階段，微裂縫區發展為宏觀裂縫.

描述裂縫尖端損傷發展的判據可以表示為:

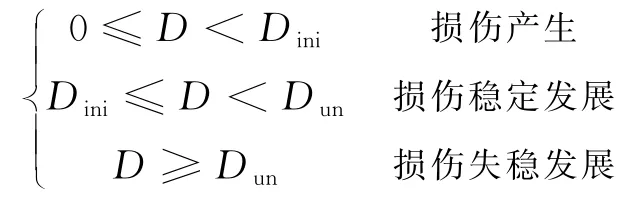
當裂縫尖端損傷為Dini時，縫尖端損傷開始穩定積累，此時宏觀裂縫處于起裂狀態，當裂縫尖端損傷為Dun時，縫端損傷開始快速失穩發展，此時宏觀裂縫已經有一定擴展長度Δac.因此，將裂縫尖端的損傷Dini，作為宏觀裂縫起裂的標志，即沿著裂縫線擴展方向，縫尖端周圍的損傷大于或等于起裂損傷Dini的區域，可以認為其為宏觀裂縫區域.

2.3 混凝土Ⅰ型裂縫失穩擴展臨界有效縫長

根據最大拉應變斷裂判據，裂縫在尖端應變達到最大拉應變時裂縫開始擴展，所以微裂紋出現可以認為是由ε1引起的，微裂紋即為損傷，因此認為損傷也是由ε1引起的.

據胡克定律，由式(3)求得主應變ε1:

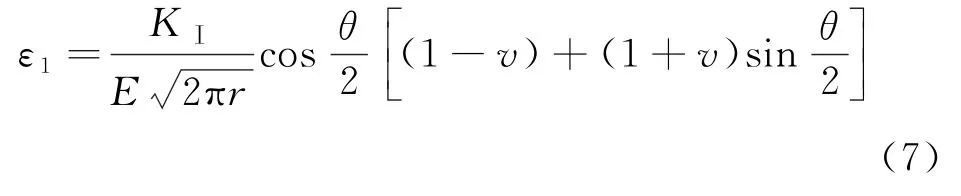
將式(7)中的ε1代入式(5)，可得:

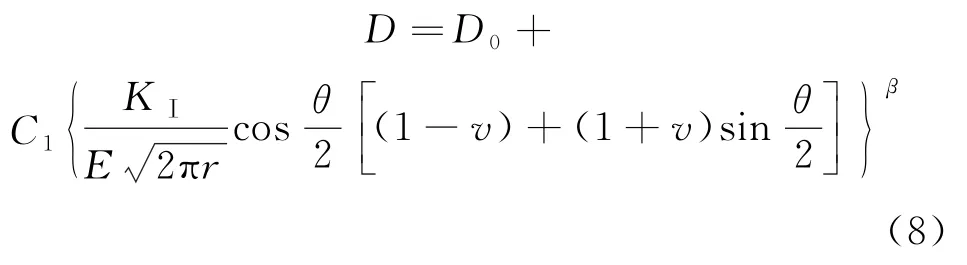
由此可得:

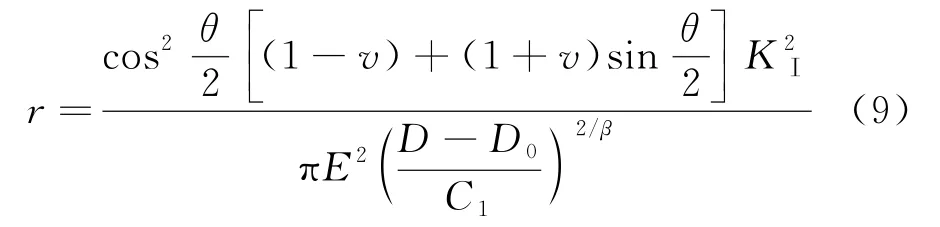
在式(8)中，可以發現，混凝土裂縫尖端的損傷隨著r的減小而不斷的增大.根據雙D判據，當裂縫尖端損傷達到Dini時，混凝土宏觀裂縫處于起裂的臨界狀態，因此，可將Dini作為裂縫起裂的標志，等價于此時宏觀裂縫已經開始逐步擴展.而隨著荷載的增加，當混凝土裂縫達到失穩擴展臨界狀態時，原有的宏觀裂縫實際上有了一定的擴展，以前述Dini作為宏觀裂縫起裂的標志，代入式(9)，可以得到損傷不小于Dini的長度范圍，即:

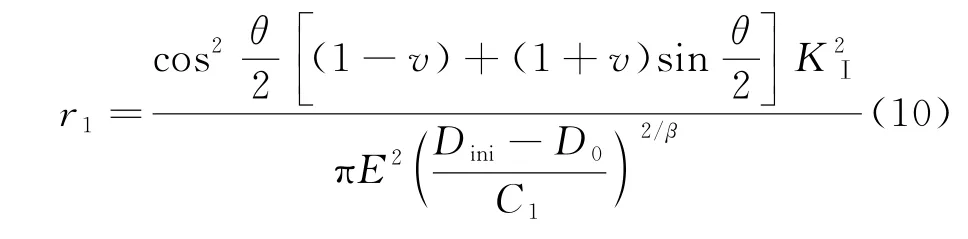
當裂縫失穩擴展時，式(8)反映了裂縫尖端區域沿著裂縫線方向的損傷變化規律.按照雙D判據，此時縫尖端的損傷為Dun，在r≤r1范圍內，始終有D≥Dini，也就代表這一區域可以等效成有效的宏觀裂縫，當r＞r1時，按照式(8)損傷不斷減小，且趨于穩定的值，即接近于混凝土初始損傷值D0.對于r＞r1的情況，依據能量守恒定律，損傷總量在等效前后始終保持不變，因此將大于初始損傷的部分損傷等效成某一區域內損傷恒定為Dini時的狀態，這一區域長度，如圖4所示，即為r2-r1.此時，整個縫尖段區域附近的損傷等效成兩部分，一部分長度定義為r2，在這個區域內損傷變量有D≥Dini，在r＞r2區域內，損傷變量保持不變為D0，r2即為等效后的臨界有效縫長增量Δac，如圖5所示，有效裂縫縫長ac=a0+Δac.由于等效前式(8)函數圖像與坐標軸圍成面積與等效后函數圖像圍成面積始終保持不變，如圖4所示，S1=S2，所以有:

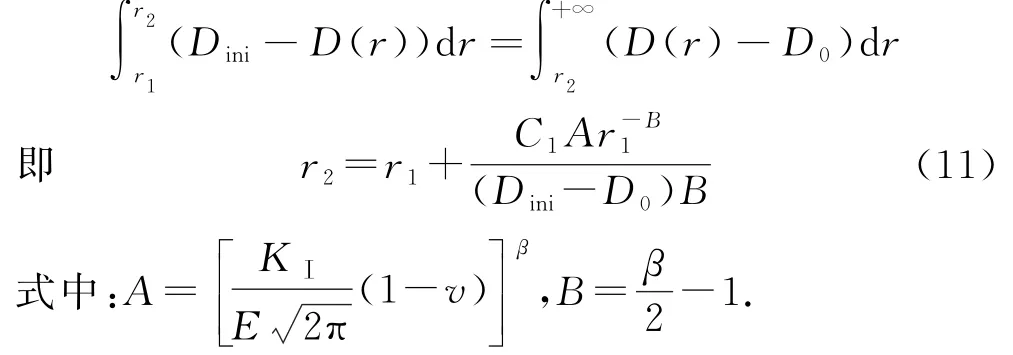
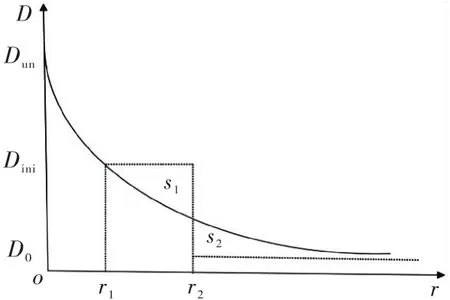
圖4 損傷等效原理圖

等效后，混凝土Ⅰ型裂縫失穩擴展時縫尖端損傷示意圖，如圖5所示.

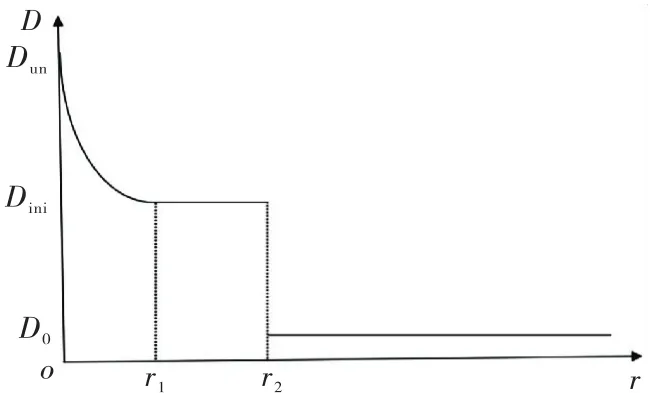
圖5 失穩狀態時等效損傷示意圖

3 Ⅰ型裂縫失穩擴展臨界有效縫長數值分析

3.1 試驗數據

一般的三點彎曲梁試件跨高比為4，常用試件凈尺寸有100 mm×100 mm×400 mm、150 mm×150 mm×600 mm、200 mm×200 mm×800 mm等.試驗采用河海系列試驗采用的試件[15]，試驗試件混凝土基本力學性能參數見表1.

表1 混凝土基本力學性能參數表

Ⅰ型裂縫試件的結構及尺寸為圖6所示，有關數據為:初始縫長a0=50 mm，試件寬度b=100 mm，試件高度h=100 mm，試件跨度S=400 mm.

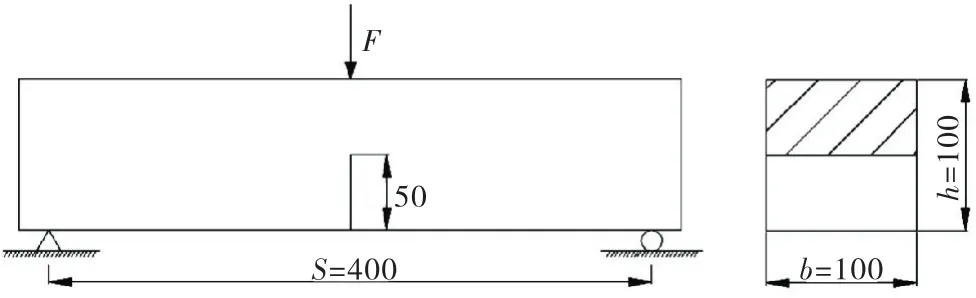
圖6 三點彎曲梁示意圖(單位:mm)

3.2 模擬計算

基于ANSYS軟件平臺，對三點彎曲梁試件進行模擬.試件采用的建模方式為先創建關鍵點，然后關鍵點連成面，在面上剖分成平面等參4節點單元(PLANE183).再沿著Z方向拉伸成8節點空間等參單元SOLID186，三點彎曲梁的有限元建模以及網格劃分如圖7所示.

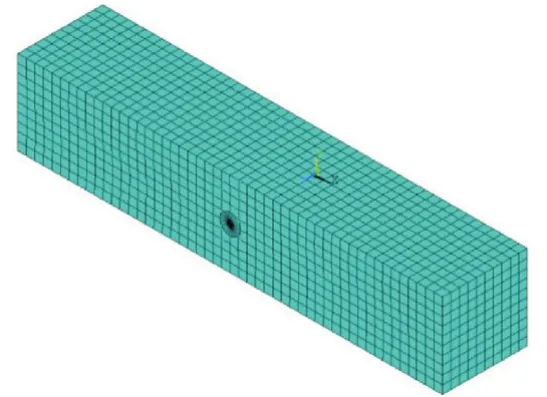
圖7 三點彎曲梁有限元網格劃分

由文獻[11]試驗可知，Ⅰ型裂縫的起裂荷載Fini為1 732 N，失穩荷載Fmax為1 820 N.

在起裂荷載Fini作用下，通過有限元計算得到Ⅰ型裂縫試驗構件裂縫尖端的應變最大值εini=1.261×10-4，根據式(8)計算得到起裂損傷值為Dini=0.226+1 935×(2.60×10-4-10-4)=0.537.

在失穩荷載Fmax作用下，通過有限元計算得到Ⅰ型裂縫試驗構件裂縫尖端的應變最大值εun=1.382×10-4，根據式(8)計算得到失穩損傷值為Dun=0.226+1 935×(2.86×10-4)=0.779.

表2 三點彎曲梁的起裂與失穩情況比較

對于本試驗中的Ⅰ型裂縫的損傷斷裂行為用雙D損傷發展判據可表述為:當混凝土材料的損傷值D≤0.537時，材料是處在材料損傷階段;當材料的損傷值0.537＜D≤0.779時，材料處于損傷穩定發展階段;當材料損傷值D＞0.779時，處于損傷失穩發展階段.

ANSYS計算結果與試驗結果比較:

根據試驗結果得到外荷載著力點的位移，δ=3.34×10-5m.

將模型的計算結果進行后處理，觀察損傷圖，如圖8～9所示.損傷區形狀類似橢圓形，在裂縫兩邊具有較好對稱性，沿裂縫面方向梯度最大，說明裂縫將沿著原方向擴展.

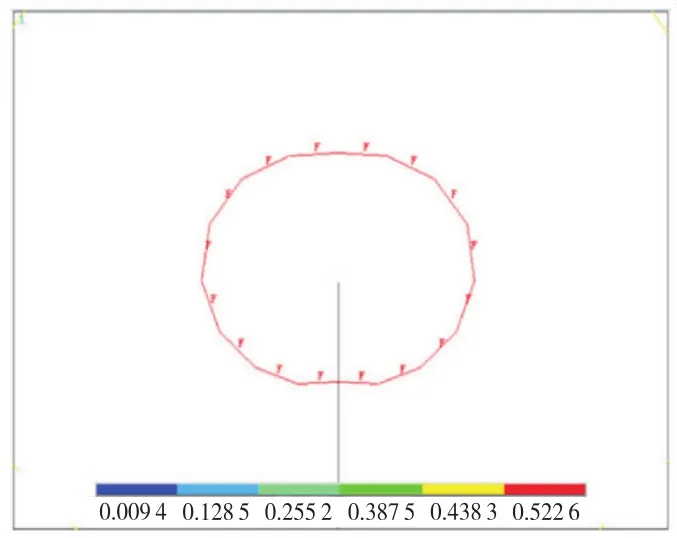
圖8 Ⅰ型裂縫起裂荷載下損傷等值線

圖9 Ⅰ型裂縫失穩荷載下損傷等值線

根據ANSYS計算得到模型y方向的位移云圖，可以讀出著力點的y方向的位移即為施加于橫梁之上集中力的著力點的位移，節點64的位移δ′=3.14×10-5m.

則其有限元結果與試驗結果的誤差為:

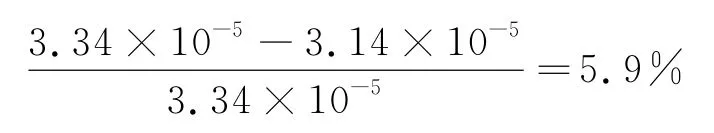
表明該模型的解析結果與實驗結果吻合很好，進一步驗證了該模型的適用性.

3.3 臨界有效縫長及失穩斷裂韌度

將試驗數據代入式(4)中計算得出Ⅰ型裂縫在失穩臨界狀態考慮斷裂過程區的臨界有效縫長ac=a0+r0=56.850 mm.

將試驗數據代入式(11)中計算得出Ⅰ型裂縫在失穩臨界狀態考慮斷裂過程區和損傷影響的臨界有效縫長ac=a0+r2=56.828 mm.

根據文獻[11]中，即課題組之前采用的利用柔度改變法計算得到的考慮斷裂過程區的有效裂縫長度ac=57.100 mm，與上述計算所得臨界有效縫長結果對比(見表3)，結果基本吻合，驗證了計算結果合理性.

表3 裂縫長度計算結果對比(單位:mm)

根據Tada給出計算縫端應力強度因子公式[11]，

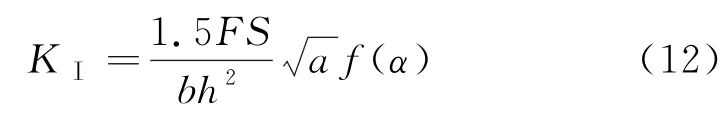
其中

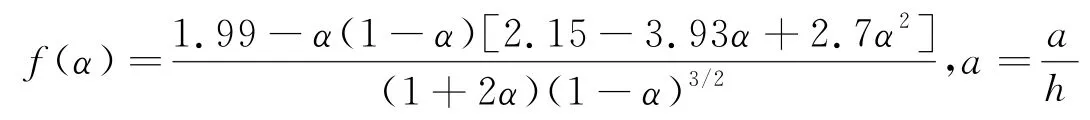
式中:KⅠ為Ⅰ型裂縫應力強度因子(MPa·m1/2);F為荷載(k N);S為兩支座間的跨度(m);h為試件高度(m);b為試件寬度(m);a為裂縫長度(m).

將上述計算所得有效裂縫長度代入式(12)計算，可得混凝土Ⅰ型裂縫臨界失穩斷裂韌度，見表4.

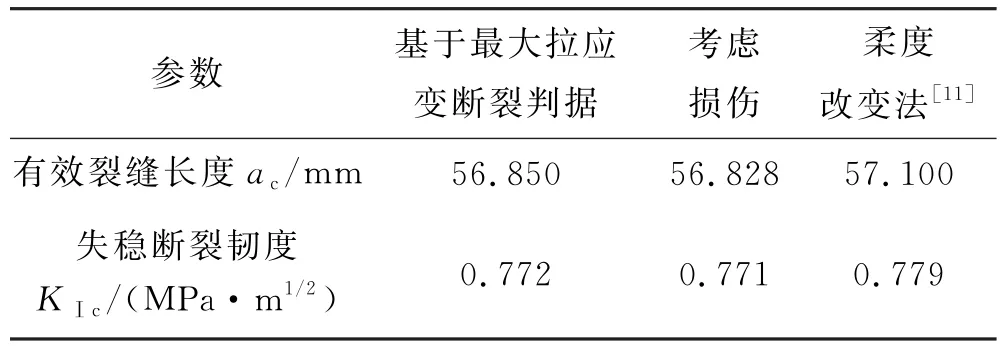
表4 失穩斷裂韌度計算結果對比

根據公式(12)，將初始裂縫長度代入，計算結果為0.613 MPa·m1/2.此結果為傳統計算斷裂韌度方法的結果，并未考慮到在裂縫失穩擴展時，初始裂縫已經有一定長度的擴展，即斷裂過程區對混凝土斷裂韌度的影響.將表4計算結果與傳統方法計算結果對比，可以發現，不管是文獻[11]采用的柔度改變法，還是本文研究所采用的方法，最后計算所得失穩斷裂韌度都比傳統計算方法大，說明傳統的判據偏于保守，對于工程材料的要求過于嚴格.而本文所采用的兩種新方法計算所得斷裂韌度大小介于傳統計算結果和柔度改變法之間，說明混凝土宏觀裂縫前端微裂縫區的斷裂與損傷會使混凝土失穩斷裂韌度有所降低，同時也說明本文方法的計算結果也是偏于安全的.

4 結 論

本文在文獻[11]的基礎上，從斷裂和損傷兩個不同的理論角度，對混凝土裂縫臨界有效縫長的計算方法進行理論研究以及數值模擬實驗計算.根據臨界有效縫長的計算結果，進一步計算失穩斷裂韌度，得到以下結論:

1)宏觀裂縫前緣存在斷裂過程區，從損傷和斷裂的角度來計算臨界有效縫長與文獻[11]采用的基于F-δ(荷載-位移)曲線得到的臨界有效縫長ac幾乎一致，說明研究方法合理，為研究混凝土Ⅰ型裂縫臨界有效縫長ac提供了兩個新思路.

2)用不同計算方法所得ac計算失穩斷裂韌度，結果表明傳統計算方法偏于保守，而本文采用的方法，不僅保證了工程上使用混凝土結構的安全性問題，同時也說明宏觀裂縫前緣區域微裂紋區損傷和斷裂對混凝土力學性能是有影響的，即采用新方法所得ac計算斷裂韌度的必要性.

3)本文Ⅰ型裂縫臨界有效縫長的研究方法，可以推廣到其他單一型裂縫以及各種復合型裂縫的臨界有效縫長的研究中，進一步研究微裂紋區斷裂和損傷對混凝土失穩斷裂韌度的影響.