滑動式Lagrange與Chebyshev插值方法對BDS精密星歷內插及其精度分析

梁 珂，周曉敏，隋立春，劉偉東

（1.自然資源部第一大地測量隊，西安 710054；2.長安大學 地質工程與測繪學院，西安 710054）

0 引言

2020年6月23日，北斗衛星導航系統（BeiDou navigation satellite system，BDS）正式完成組網，成為全球衛星導航系統（global navigation satellite system, GNSS）家族中的一員。與全球定位系統（global positioning system，GPS）相比，BDS導航衛星星座由混合星座組成，包括地球靜止軌道（geostationary Earth orbit, GEO）衛星、傾斜地球同步軌道（inclined geosynchronous orbits, IGSO）衛星、中圓地球軌道（medium Earth orbit, MEO）衛星[1-3]。BDS在定位過程中，需要分析中心提供精密星歷獲取衛星三維坐標信息[4]。一般提供的精密星歷產品文件時間間隔為 15 min，但是接收機的采樣間隔時間一般為30、10 或1 s，因此，BDS在定位過程需要獲取任意時刻衛星三維坐標信息。獲取任意歷元 BDS衛星三維位置成為 BDS定位過程中需解決的問題之一[5]。國內外學者研究表明：插值法是獲取任意歷元BDS衛星三維位置最簡單、高效的方法之一[6]。目前對 BDS精密星歷插值的數學方法主要包括：埃爾米特（Hermite）插值、三角函數插值、拉格朗日（Lagrange）插值、牛頓（Newton）插值、切比雪夫（Chebyshev）插值、三次樣條插值等。文獻[7]對比分析了滑動式與非滑動式Lagrange插值方法對BDS精密星歷進行內插結果的影響，其結果表明，滑動式 Lagrange插值效果明顯優于非滑動式 Lagrange插值效果，滑動式Lagrange插值對GEO、IGSO、MEO衛星插值都能達到毫米級精度；文獻[8] 對比滑動式傅里葉級數插值與9階Chebyshev插值對比分析，其結果表明，9階Chebyshev插值更適用于GEO衛星與IGSO衛星，而MEO衛星使用傅里葉級數插值精度更高；文獻[9] 采用 Lagrange插值與Chebyshev插值對精密星歷進行內插對比分析，結果表明：采用一定的階數精密星歷內插均可以達到毫米級精度，且二者插值效果接近。本文基于滑動式 Lagrange插值和 Chebyshev插值方法，分別對BDS三種不同衛星精密星歷內插，對比分析二者插值方法的特點和精度，旨在為今后BDS定位過程中獲取任意歷元衛星三維坐標信息提供參考。

1 插值數學模型

1.1 Lagrange插值數學模型

Lagrange插值法為：假設y=f(xi)在區間[a,b]上是個實函數，且在區間[a,b]上n+1階可導，那么在區間[a,b]上任意一點x的n階Lagrange插值多項式代數表達式為

式中：f(x)為插值節點處函數值；n為插值多項式的階數；為插值基函數，僅與插值節點有關。

對BDS精密星歷進行n階Lagrange內插，在插值時選擇一個區間[t0,t1]，即可求出任意時刻衛星在X、Y和Z方向上的坐標分量，從而得到任意歷元衛星的位置。任意歷元衛星位置表示為

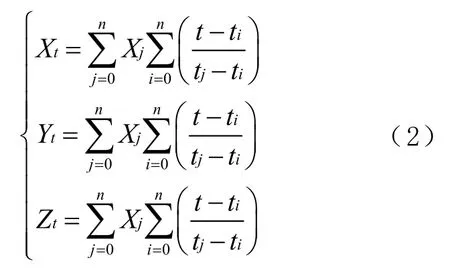
式中：i≠ j，（Xt、Yt、Zt）為t時刻衛星位置三維坐標分量；ti、tj為插值區間任意常數。

Lagrange插值方法在插值兩端易產生“龍格”現象，為進一步提高BDS精密星歷內插的精度，使用滑動式Lagrange插值方法獲取任意歷元衛星三維坐標分量，可以有效避免“龍格”現象的產生[7-8]。

滑動式Lagrange插值方法為：在進行Lagrange插值時，不斷改變插值區間，使待插值點一直保持在插值區間的中間點上，以此來提高插值的精度。滑動式 Lagrange插值可以抑制插值區間兩端插值結果的震蕩[9-10]，使插值結果精度達到最優。對BDS精密星歷進行n階Lagrange內插，當n為偶數時，生成n-1（奇數）階插值多項式，若選擇12個插值節點，可以生成11階插值多項式，此時求得的插值結果只保留第 4個和第 5個插值節點中間的插值結果；當n為奇數時，生成n-1（偶數）階插值多項式，若選擇 13個插值節點，可以生成12階插值多項式，此時求得的插值結果只保留第5個和第6個、第6個和第7個插值節點中間的插值結果，將其他節點插值結果舍去。

1.2 Chebyshev插值數學模型

Chebyshev多項式擬合是采用函數最佳逼近的原理，根據已知節點生成一個函數，使其在給定點的函數值與該點函數值之間的方差和最小，且該函數是以Chebyshev多項式為基函數構成的。如果在區間[t0,t0+Δt]內的衛星星歷使用Chebyshev多項式進行擬合，同時將衛星軌道進行標準化處理，對時間進行轉換，將其定義為

式中：t∈[?1 ,1]，t0和?t分別為開始歷元與擬合區間的長度；t為區間[t0,t0 +Δt]中任意常數，此時衛星三維坐標分量（Xt、Yt、Zt）可表示為

式中：aXi、aYi、aZi分別為相應分量的Chebyshev多項式的系數；Ti(τt) 為Chebyshev多項式。

2 算例分析

為對比分析不同階數滑動式 Lagrange插值與Chebyshev插值方法對 BDS精密星歷的精度，本文借助武漢大學國際 GNSS服務（International GNSS Service, IGS）數據中心提供的BDS精密星歷產品，采用滑動式 Lagrange插值與 Chebyshev插值方法分別對 GEO衛星、IGSO衛星、MEO衛星精密星歷進行內插，實驗流程如圖1所示。圖1中：RMS（root mean square error）為均方根誤差。

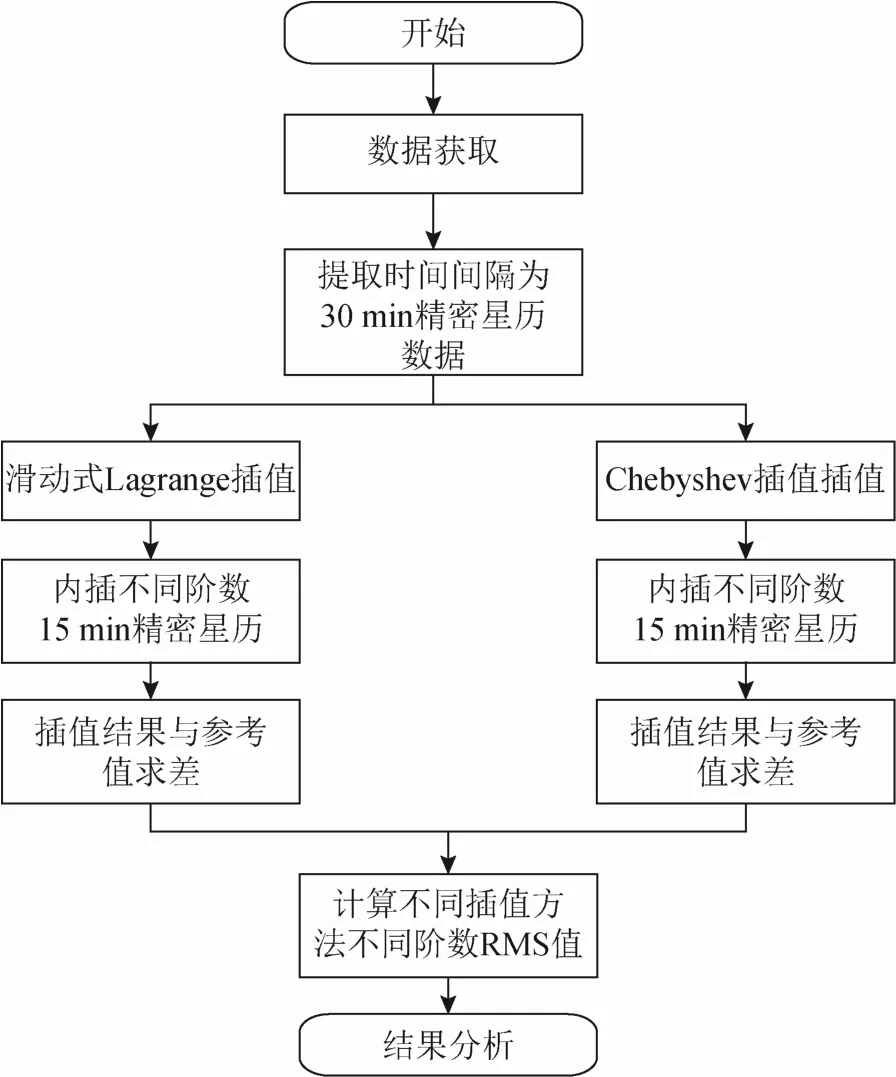
圖1 實驗流程

本次實驗數據起始歷元為2020-01-01 T 00:00:00，終止歷元為2020-01-02 T 23:30:00，為Lagrange插值方法和Chebyshev插值方法的區間長度，以BDS精密星歷產品中，每30 min間隔的衛星三維坐標作為已知點，以每15 min間隔的衛星三維坐標作為參考值，將計算得到的內插值與參考值進行求差得到殘差，以殘差的均方差根結果表示插值的精度因子。本次實驗觀測中任選 PC02（GEO衛星）、PC08（IGSO衛星）、PC12（MEO衛星）三顆衛星分別進行5階至20階滑動式Lagrange插值和Chebyshev插值，對其結果進行統計分析，其結果如表1至表3所示，為了更加直觀反映出插值結果，將插值結果可視化輸出，結果如圖2至圖7所示。

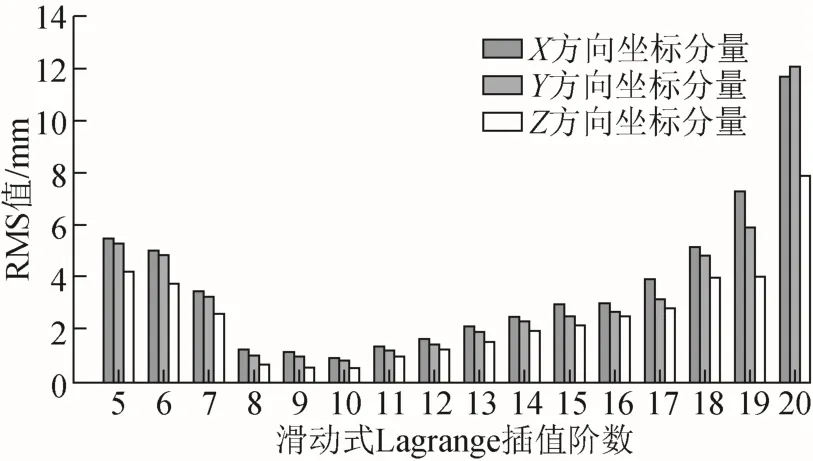
圖2 不同階數滑動式Lagrange插值方法對GEO衛星的影響

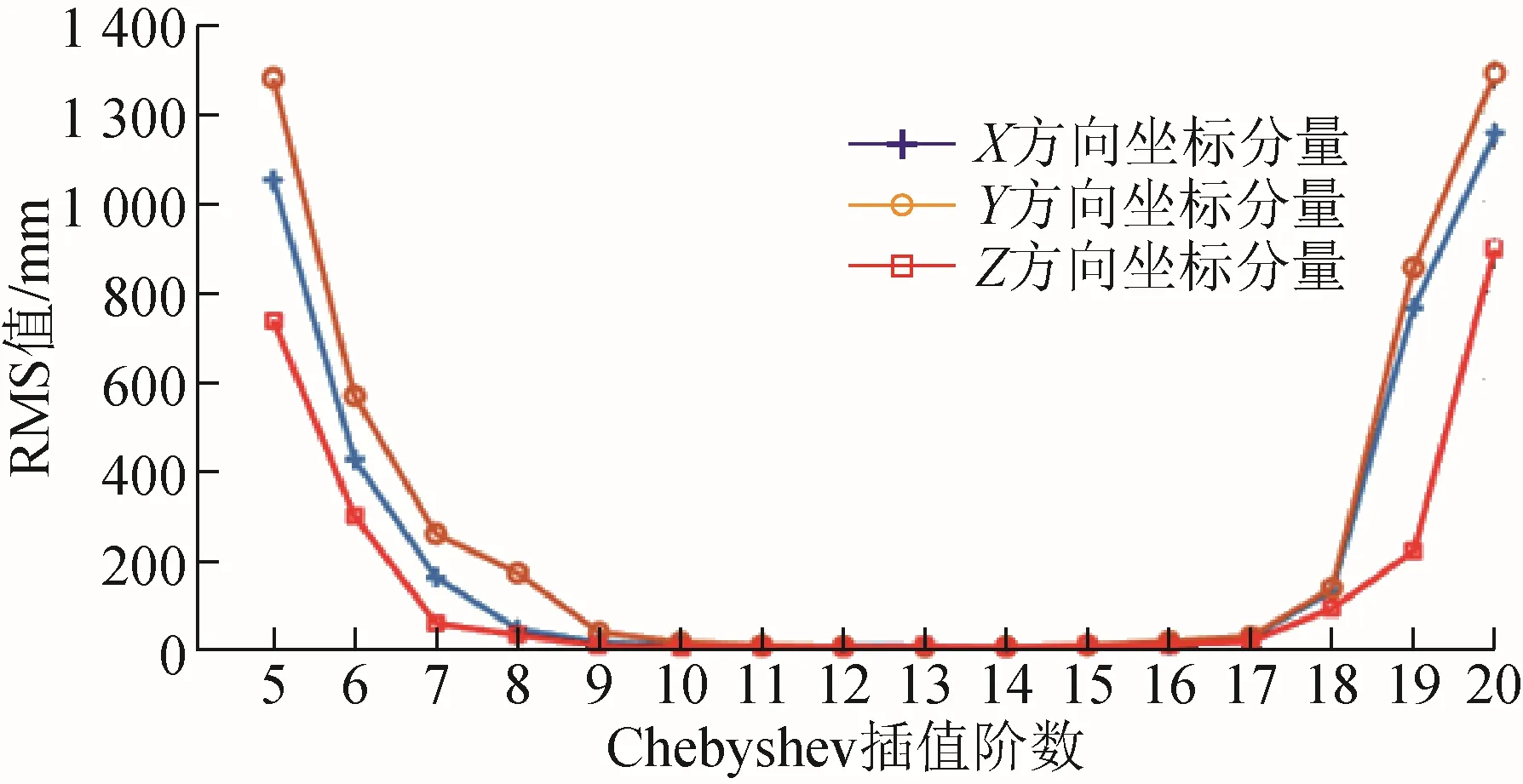
圖7 不同階數Chebyshev插值方法對MEO衛星的影響

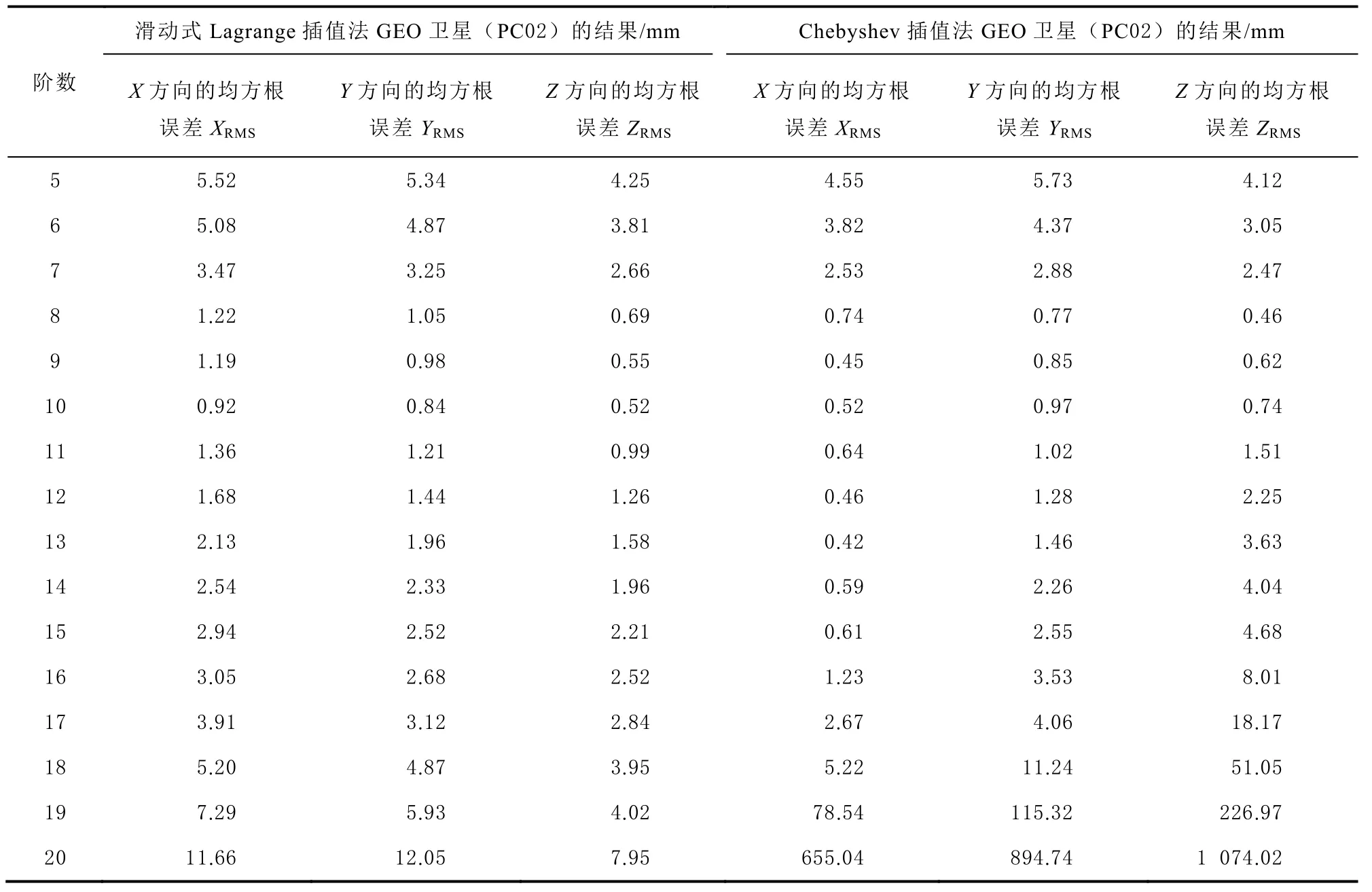
表1 不同階數滑動式Lagrange插值和Chebyshev插值對GEO衛星的影響

表3 不同階數滑動式Lagrange插值和Chebyshev插值對MEO衛星的影響

2.1 GEO衛星精密星歷內插精度分析

基于滑動式Lagrange插值方法對GEO衛星精密星歷進行內插，由表1和圖2可以看出：5~19階滑動式Lagrange插值對GEO衛星精密在X、Y、Z方向坐標分量均可達到毫米級精度，當使用10階滑動式Lagrange插值時，GEO衛星精密星歷三維坐標分量精度達到最高，RMS值分別為0.92、0.84、0.52 mm；滑動式Lagrange插值階數在5~10階時，隨著插值階數的增加，插值精度隨之提升，此時Z方向坐標分量插值精度最佳，X方向坐標分量插值精度最差；滑動式Lagrange插值階數在11~20階時，隨著插值階數的增加，插值精度反而降低，此時Z方向坐標分量插值精度最佳，X方向坐標分量插值精度最差。

基于Chebyshev插值方法對GEO衛星精密星歷進行內插，由表1和圖3可以看出：5~16階Chebyshev插值對GEO衛星精密在X、Y、Z方向坐標分量均可達到毫米級精度，當使用 9階Chebyshev插值時，GEO衛星精密星歷三維坐標分量精度達到最高，RMS值分別為0.45、0.85、0.62 mm；Chebyshev插值階數在5~9階時，隨著插值階數的增加，插值精度隨之提升，Chebyshev插值階數在8~10階時，GEO衛星精密星歷三維坐標分量精度均達到亞毫米級精度，且精度相當；Chebyshev插值階數在13~20階時，隨著插值階數的增加，插值精度反而降低，此時X方向坐標分量插值精度最佳，Z方向坐標分量插值精度最差。對GEO衛星而言，與Chebyshev插值方法相比滑動式Lagrange插值方法有效避免“龍格”現象的產生。

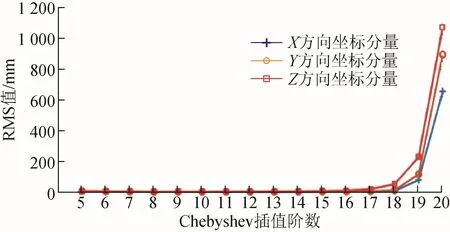
圖3 不同階數Chebyshev插值方法對GEO衛星的影響

2.2 IGSO衛星精密星歷內插精度分析

基于滑動式 Lagrange插值方法對 IGSO衛星精密星歷進行內插，由表2和圖4可以看出：8~17階滑動式 Lagrange插值對 IGSO衛星精密在X、Y、Z方向坐標分量均可達到毫米級精度，當使用14階滑動式Lagrange插值時，IGSO衛星精密星歷三維坐標分量精度達到最高，RMS值分別為0.85、1.28、1.38 mm；滑動式Lagrange插值階數在5~14階時，隨著插值階數的增加，插值精度隨之提升，此時X方向坐標分量精度最佳，Z方向坐標分量精度最差；滑動式Lagrange插值階數在15~20階時，隨著插值階數的增加，插值精度反而降低，此時X方向坐標分量插值精度最佳，Z方向坐標分量插值精度最差。

表2 不同階數滑動式Lagrange插值和Chebyshev插值對IGSO衛星的影響

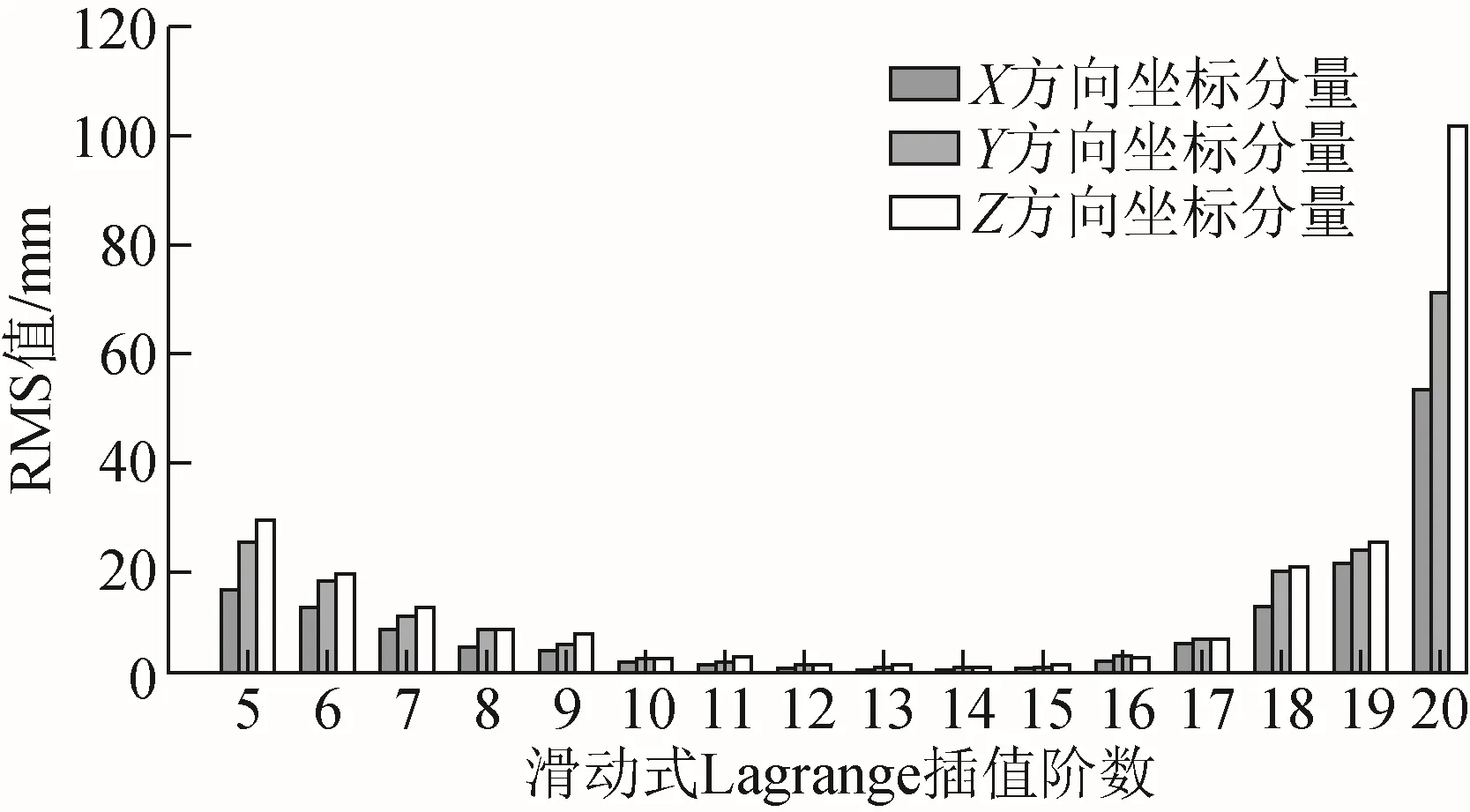
圖4 不同階數滑動式Lagrange插值方法對IGSO衛星的影響

基于Chebyshev插值方法對IGSO衛星精密星歷進行內插，由表2和圖5可以看出：10~17階Chebyshev插值對IGSO衛星精密在X、Y、Z方向坐標分量均可達到毫米級精度，當使用 14階Chebyshev插值時，IGSO衛星精密星歷X方向坐標分量、Y方向坐標分量精度達到最高，RMS值分別為0.79、1.30 mm，當使用15階Chebyshev插值時，IGSO衛星精密星歷Z方向坐標分量精度達到最高，RMS值為0.62 mm，Chebyshev插值階數在5~14階時，隨著插值階數的增加，插值精度隨之提升，Chebyshev插值階數在15~20階時，隨著插值階數的增加，插值精度反而降低；5~11階時，Z方向坐標分量插值精度最佳，Y方向坐標分量插值精度最差。

圖5 不同階數Chebyshev插值方法對IGSO衛星的影響

2.3 MEO衛星精密星歷內插精度分析

基于滑動式Lagrange插值方法對MEO衛星精密星歷進行內插，由表3和圖6可以看出：9~17階滑動式Lagrange插值對MEO衛星精密在X、Y、Z方向坐標分量均可達到毫米級精度，當使用14階滑動式Lagrange插值時，MEO衛星精密星歷三維坐標分量精度達到最高，RMS值分別為0.79、1.41、1.15 mm；滑動式Lagrange插值階數在5~14階時，隨著插值階數的增加，插值精度隨之提升，滑動式Lagrange插值階數在 15~20階時，隨著插值階數的增加，插值精度反而降低；滑動式 Lagrange插值階數在 5~9階時，Z方向坐標分量插值精度最佳，Y方向坐標分量插值精度最差，滑動式Lagrange插值階數在 10~14階時，X方向坐標分量插值精度最佳，Y方向坐標分量插值精度最差，滑動式Lagrange插值階數在 15~20階時，Y方向坐標分量插值精度最佳，X方向坐標分量插值精度最差。

圖6 不同階數滑動式Lagrange插值方法對MEO衛星的影響

基于Chebyshev插值方法對MEO衛星精密星歷進行內插，由表3和圖7可以看出：11~15階Chebyshev插值對MEO衛星精密在X、Y、Z方向坐標分量可達到毫米級精度，當使用 11階Chebyshev插值時，MEO衛星精密星歷Z坐標分量精度達到最高，RMS值為3.22 mm，當使用13階Chebyshev插值時，MEO衛星精密星歷Y坐標分量精度達到最高，RMS值為 3.44 mm，當使用14階Chebyshev插值時，MEO衛星精密星歷Z坐標分量精度達到最高，RMS值為 3.34 mm；Chebyshev插值階數在5~11階時，隨著插值階數的增加，插值精度隨之提升，Chebyshev插值階數在 14~20階時，隨著插值階數的增加，插值精度降低。對MEO衛星而言，與Chebyshev插值方法相比，滑動式Lagrange插值方法有效避免“龍格”現象的產生。

3 結束語

本文借助武漢大學IGS數據中心提供的BDS精密星歷產品，基于滑動式 Lagrange插值和Chebyshev插值方法對三種類型軌道衛星進行精密星歷插值分析，實驗結果表明：滑動式Lagrange插值和Chebyshev插值方法對GEO衛星精密星歷最佳可達到亞毫米級精度，對IGSO、MEO衛星精密星歷最佳可達到毫米級精度，均可滿足高精度導航定位的需求；與Chebyshev插值方法相比，滑動式 Lagrange插值方法有效避免“龍格”現象的產生；滑動式Lagrange插值和Chebyshev插值方法的階數均不宜過高或過低，同一種插值方法對應不同衛星所達到最佳精度時階數不同，同一衛星對應不同的插值方法最佳精度時階數亦不相同。因此，今后在獲取任意時刻BDS精密星歷時，需針對不同衛星采取不同插值方法不同階數以達到插值精度效果最佳的目的。