多星座組合RAIM技術(shù)在列車定位中的應(yīng)用
鐵凱博,米根鎖,王彥快
(蘭州交通大學(xué), 自動化與電氣工程學(xué)院, 蘭州 730070)
0 引言
列車定位精度直接影響列車的運(yùn)行安全,提高列車定位的精度和可靠性已經(jīng)成為不可忽視的重要目標(biāo)[1]。全球衛(wèi)星導(dǎo)航系統(tǒng)(global navigation satellite system, GNSS)在鐵路領(lǐng)域已廣泛應(yīng)用,但在列車實(shí)際運(yùn)行過程中,衛(wèi)星出現(xiàn)故障,會導(dǎo)致定位結(jié)果不準(zhǔn)確[2],這就要求導(dǎo)航系統(tǒng)能對所用衛(wèi)星進(jìn)行實(shí)時(shí)檢測,剔除出現(xiàn)故障的衛(wèi)星。因此,有學(xué)者提出將接收機(jī)自主完好性監(jiān)測(receiver autonomous integrity monitoring,RAIM)技術(shù)[3]應(yīng)用于列車定位。文獻(xiàn)[4]提出了RAIM技術(shù)在列車定位中的可用性預(yù)測方法,并對該技術(shù)在鐵路領(lǐng)域內(nèi)的可用性做出了判斷;文獻(xiàn)[5]將RAIM技術(shù)應(yīng)用于北斗衛(wèi)星導(dǎo)航系統(tǒng)(BeiDou navigation satellite system,BDS)的列車定位中,提出沿股道水平保護(hù)級(along track protect level,ATPL)算法,提高了RAIM技術(shù)在列車定位中的可用性;文獻(xiàn)[6]分析了BDS完好性問題在列車定位中的風(fēng)險(xiǎn),并設(shè)計(jì)了BDS RAIM可用性預(yù)測系統(tǒng),保障了RAIM預(yù)測結(jié)果的可靠性;文獻(xiàn)[7]在故障衛(wèi)星檢測環(huán)節(jié)中引入加權(quán)因子,降低檢測過程中的漏警率,提高了列車定位精度。文獻(xiàn)[8]解決了GNSS性能指標(biāo)與鐵路可用性指標(biāo)的映射問題,為基于GNSS的 RAIM 算法在鐵路領(lǐng)域中的應(yīng)用提供了參考。通過分析文獻(xiàn)可知:目前主要針對單星座RAIM 在列車定位中的應(yīng)用進(jìn)行了研究,單星座RAIM應(yīng)于列車定位時(shí),常會出現(xiàn)因可見星不足或幾何分布較差而降低算法可用性的情況,進(jìn)而影響算法的故障檢測率和故障識別率。由于可見星數(shù)目的限制,單星座 RAIM 在某些高海拔鐵路定位精度并不高[9],甚至不能使用,RAIM算法在鐵路領(lǐng)域內(nèi)的研究還處于起步階段。
鑒于此,本文提出了將多星座RAIM技術(shù)應(yīng)用于列車定位,通過增加可見星數(shù)目提高RAIM算法的可用性。在構(gòu)造多星座系統(tǒng)觀測方程的基礎(chǔ)上,采用奇偶矢量法對導(dǎo)航衛(wèi)星進(jìn)行故障檢測。通過青藏鐵路列車定位數(shù)據(jù)對全球定位系統(tǒng)(global positioning system, GPS)、伽利略衛(wèi)星導(dǎo)航系統(tǒng)(Galileo satellite navigation system, Galileo)和 BDS多星座組合RAIM和GPS單星座RAIM進(jìn)行對比仿真,分析多星座RAIM在列車定位中的檢測性能。
1 多星座系統(tǒng)列車定位原理
1.1 時(shí)空基準(zhǔn)統(tǒng)一
為構(gòu)成基于列車定位的多星座導(dǎo)航系統(tǒng),需將不同星座的時(shí)間系統(tǒng)進(jìn)行統(tǒng)一,坐標(biāo)系統(tǒng)進(jìn)行轉(zhuǎn)換,采用相同的時(shí)間和坐標(biāo)標(biāo)準(zhǔn),實(shí)現(xiàn)多星座系統(tǒng)的數(shù)據(jù)融合[10-11]。本文將多星座時(shí)間、坐標(biāo)系統(tǒng)統(tǒng)一轉(zhuǎn)換為以GPS為基準(zhǔn)。轉(zhuǎn)換過程如下:
1)將Galileo系統(tǒng)時(shí)(Galileo system time, GST)轉(zhuǎn)化為GPS時(shí)(GPS time, GPST)的計(jì)算公式為

式中:TGPST為 GPS時(shí);TGST為 Galileo系統(tǒng)時(shí);TGGTO為GPST與GST間的偏差;A0G、A1G、t0G和SWNOG分別為時(shí)間偏差的常數(shù)項(xiàng)、變化率、參考時(shí)間和參考星期個(gè)數(shù);TTOW為星期內(nèi)的時(shí)間;T是常數(shù),為604 800;SWN為Galileo的星期個(gè)數(shù);mod為求余函數(shù)。
2)將北斗時(shí)(BDS time, BDT)轉(zhuǎn)化為GPST的計(jì)算公式為
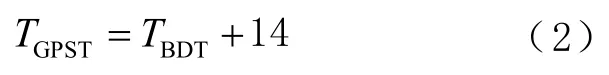
式中,TBDT為北斗系統(tǒng)時(shí)。
3)將格洛納斯衛(wèi)星導(dǎo)航系統(tǒng)(global navigation satellite system, GLONASS)時(shí)(GLONASS time,GLONASST)轉(zhuǎn)化為GPST的計(jì)算公式為
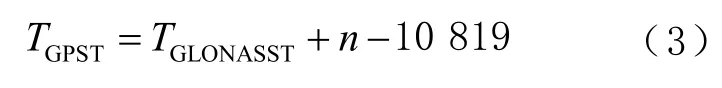
式中:TGLONASST為GLONASS時(shí);n為協(xié)調(diào)世界時(shí)(coordinated universal time, UTC)與國際原子時(shí)(international atomic time, TAI)之間不斷調(diào)整的參數(shù),由國際地球自轉(zhuǎn)服務(wù)組織(International Earth Rotation Service, IERS)提供。
GPS采用1984世界大地坐標(biāo)系(world geodetic coordinate system 1984, WGS84);Galileo采用伽利略地球參考框架(Galileo terrestrial reference frame,GTRF);BDS采用北斗坐標(biāo)系(BeiDou coordinate system,BDCS);GLONASS采用俄羅斯大地坐標(biāo)框架(Parametry Zelmy1990, PZ90)。由于列車偽距定位的精度為米級,BDCS坐標(biāo)和GTRF坐標(biāo)轉(zhuǎn)換為WGS84坐標(biāo)產(chǎn)生的誤差可以忽略不計(jì)[12],只需將PZ90坐標(biāo)轉(zhuǎn)換為WGS84坐標(biāo)即可,采用布爾薩-沃爾夫(Bursa-Wolf)模型[13]進(jìn)行PZ90和WGS84間的坐標(biāo)轉(zhuǎn)換,Bursa-Wolf模型亦稱為黑爾默特(Helmert)7參數(shù)模型,其計(jì)算公式為
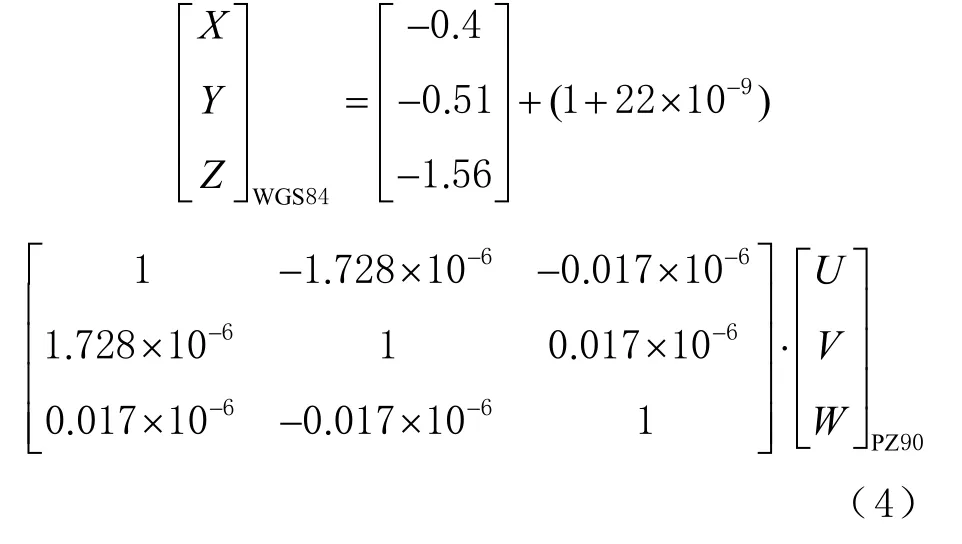
1.2 列車定位原理
在列車運(yùn)行過程中,可見星連續(xù)不斷地向車載接收機(jī)發(fā)送星歷參數(shù)和時(shí)間信息,車載計(jì)算機(jī)計(jì)算出與N顆可見星之間的偽距(ρ1,ρ2,ρ3,…,ρN),通過聯(lián)立方程進(jìn)行列車位置的定位解算,即
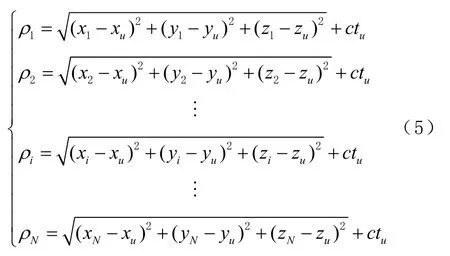
式中:ρi(i=1,2,...,N)為第i號衛(wèi)星到車載接收機(jī)的偽距,N為可見星數(shù)目;(xi,yi,zi)為第i號衛(wèi)星的空間位置;(xu,yu,zu)為列車位置;c為光速;tu為車載接收機(jī)與衛(wèi)星間的鐘差,其定位原理如圖1所示。
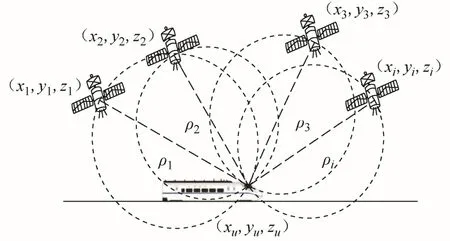
圖1 列車偽距定位原理
若參與解算的可見星發(fā)生故障,會造成ρi的測量值出現(xiàn)偏差,導(dǎo)致列車定位解算結(jié)果不準(zhǔn)確。因此,需在列車定位解算之前,采用RAIM技術(shù)對衛(wèi)星的健康狀況進(jìn)行判斷,剔除出現(xiàn)故障的衛(wèi)星。
2 基于列車定位的多星座RAIM算法
在列車定位中,RAIM算法采用冗余技術(shù)對車載接收機(jī)接收到的導(dǎo)航信息進(jìn)行一致性校驗(yàn),其本質(zhì)是通過增加可見星數(shù)目來增加信息冗余,實(shí)現(xiàn)對衛(wèi)星的故障檢測[14]。當(dāng)列車導(dǎo)航系統(tǒng)至少監(jiān)測到4顆衛(wèi)星時(shí),可進(jìn)行用戶位置的定位解算;至少監(jiān)測到5顆衛(wèi)星時(shí),可實(shí)現(xiàn)故障衛(wèi)星的檢測;至少監(jiān)測到6顆衛(wèi)星時(shí),可對故障衛(wèi)星進(jìn)行識別。因此,可見星數(shù)目對 RAIM 算法的可用性有很大影響,通過采用多星座系統(tǒng)增加可見星數(shù)目進(jìn)而改善幾何分布情況對 RAIM 算法的可用性會有相應(yīng)提升[15]。
在鐵路沿線中,海拔較高時(shí),會使部分衛(wèi)星的檢測效果變差[16],影響算法的可用性。多星座組合系統(tǒng)通過增加線路中可見衛(wèi)星數(shù)目增加冗余觀測信息,進(jìn)而提高 RAIM 算法在列車定位中的可用性。當(dāng)車載接收機(jī)監(jiān)測到的可見衛(wèi)星數(shù)N>n時(shí)(n=4+m,m為星座數(shù)),可進(jìn)行故障衛(wèi)星的檢測與識別。對于單星座系統(tǒng)至少監(jiān)測到n=4+1=5顆衛(wèi)星;對于雙星座系統(tǒng)至少監(jiān)測到n=4+2=6顆衛(wèi)星;對于三星座系統(tǒng)至少監(jiān)測到n=4+3=7顆衛(wèi)星;以此類推。圖2為多星座 RAIM算法的程序流程圖。圖2中n為故障檢測所需的最少可見星數(shù)。
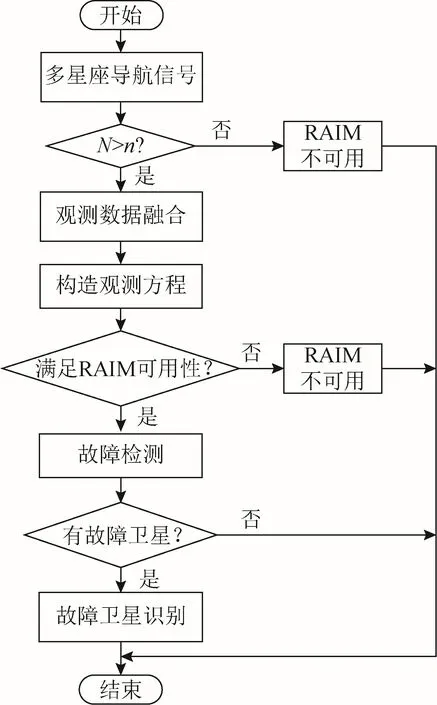
圖2 多星座RAIM算法程序流程
2.1 構(gòu)造多星座系統(tǒng)觀測方程
假設(shè)在某一時(shí)刻共有N顆可見星,對式(5)進(jìn)行泰勒展開,并考慮觀測誤差,線性化后的多星座系統(tǒng)觀測方程為

式中:y?RN×1為觀測偽距與計(jì)算偽距的差值;x?Rl×1為列車的三維位置信息和m個(gè)星座對應(yīng)的時(shí)鐘誤差參數(shù),l=m+3;ε?RN×1為觀測偽距噪聲矢量,服從均值為 0,方差為的正態(tài)分布。H?RN?l為N ?l維的觀測矩陣,其表達(dá)式為

式中:A為列車與衛(wèi)星之間的方向余弦值;B為對應(yīng)的各星座車載接收機(jī)鐘差;Aij(i=1,…,m,j=1,…,3)為對應(yīng)第i個(gè)星座觀測矩陣Ai的第j列元素,Ai可表示為
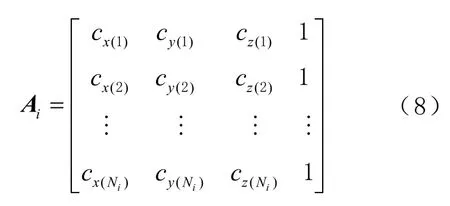
2.2 基于奇偶矢量法的故障衛(wèi)星檢測識別
假設(shè)偽距誤差ε=O,則系統(tǒng)的線性化觀測方程為

將系數(shù)矩陣H分解成

式中:Q是N?N階的正交矩陣;R為N?l階的上三角矩陣;O為零矩陣。
將式(10)代入式(9)并左乘QT,可得

式中,QT和R可分別表示為
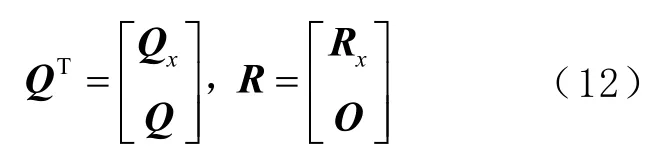
式中:Qx為QT的前l(fā)行,Q為QT的后N-l行;Rx為R的前l(fā)行,O是R的后N-l行,為零矩陣。
將式(12)代入式(11)中可得
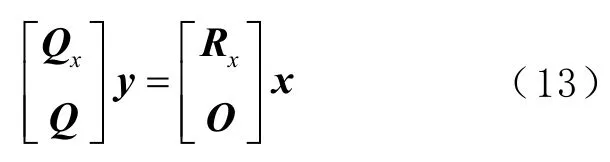
可得最小二乘解

若考慮到觀測誤差ε,即y=Hx+ε ,則有

式中:p為奇偶空間上的奇偶矢量;Q為奇偶空間矩陣;奇偶空間矢量p是由ε在奇偶空間矩陣Q上投影所得,可反映故障衛(wèi)星偏差量等信息。因此,可基于奇偶矢量p構(gòu)造檢測統(tǒng)計(jì)量,進(jìn)行故障衛(wèi)星的檢測識別。
衛(wèi)星偽距殘差向量平方和為v=pTp。根據(jù)統(tǒng)計(jì)分布理論,當(dāng)偽距噪聲矢量ε中的各個(gè)分量相互獨(dú)立,且服從均值為 0,方差為的正態(tài)分布時(shí),v/服從自由度為N-l的中心X2分布;均值不為0時(shí),v/服從自由度為N?l的非中心χ2分布,非中心參數(shù)為λ,即
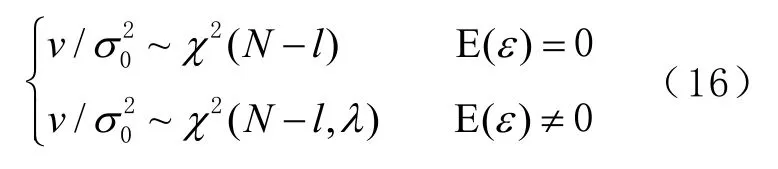
構(gòu)造檢驗(yàn)統(tǒng)計(jì)量ri為

式中:ri為第i顆衛(wèi)星的檢驗(yàn)統(tǒng)計(jì)量;Qi為第i顆衛(wèi)星的奇偶空間矩陣。
已知誤警率PFA,則有
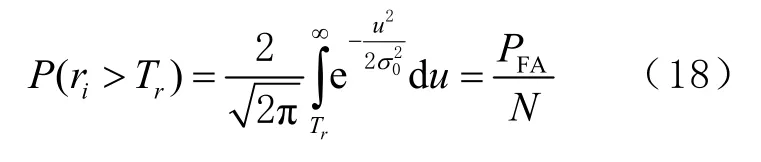
式中:P(ri>Tr)為檢測統(tǒng)計(jì)量大于檢測門限的概率,為標(biāo)準(zhǔn)正態(tài)分布的概率密度函數(shù)。
根據(jù)式(18)可求出檢測門限Tr,將每個(gè)檢測統(tǒng)計(jì)量ri與Tr進(jìn)行比較,若ri>Tr,說明第i顆衛(wèi)星出現(xiàn)故障。
2.3 多星座RAIM算法可用性判斷
為保障列車定位結(jié)果的可靠性,在可見星數(shù)目達(dá)到要求后,還需對沿線可見星的空間幾何分布進(jìn)行預(yù)測,對RAIM算法的可用性進(jìn)行判斷。
本文采用水平保護(hù)級(horizontal protect level,HPL)THPL來判斷RAIM可用性。根據(jù)車載接收機(jī)接收到的列車定位數(shù)據(jù)計(jì)算THPL值,當(dāng)THPL小于水平告警閾值(horizontal alert limit,HAL)THAL時(shí),算法可用,反之則無效,車載需重新接收衛(wèi)星信號進(jìn)行可用性判斷。
利用最大特征斜率Lmax乘以臨界偏差Pbias計(jì)算出THPL的值。首先,計(jì)算每顆衛(wèi)星的特征斜率為
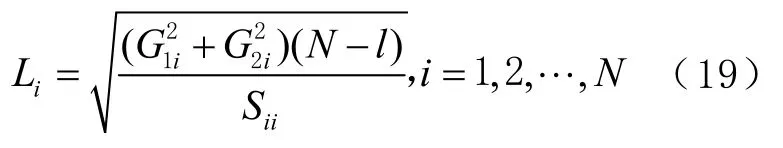
式中:Li為第i顆衛(wèi)星的特征斜率;G1i、G2i分別為矩陣G中元素,G= (HTH)?1HT;S為矩陣ii S的對角元素,S=I? (HTH)?1HT。
然后根據(jù)檢測門限Tr,基于漏檢概率PMD計(jì)算出臨界偏差Pbias=σ0., λ的計(jì)算方法為
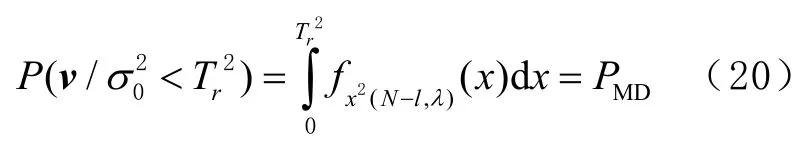
水平保護(hù)限值可由式(21)計(jì)算出,即
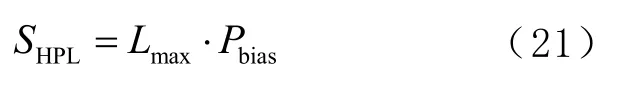
式中,SHPL為計(jì)算出的水平保護(hù)限值。
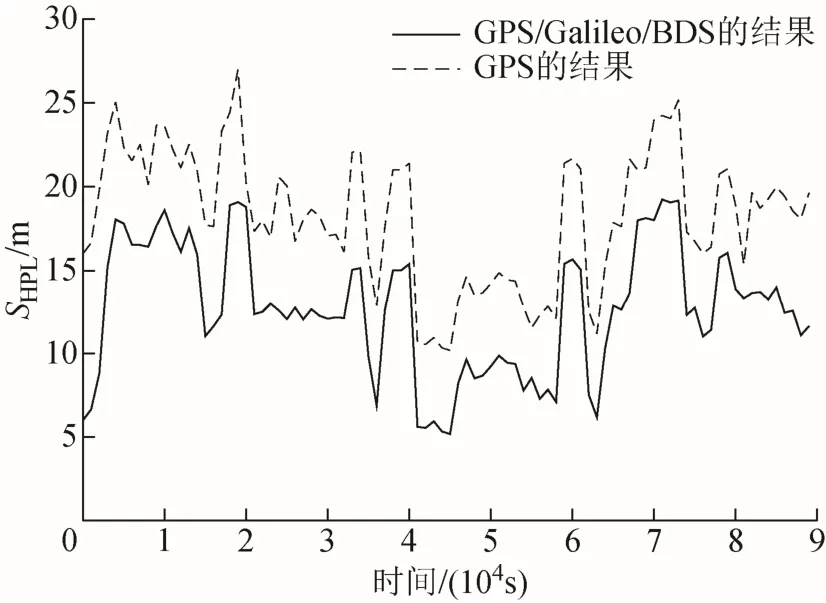
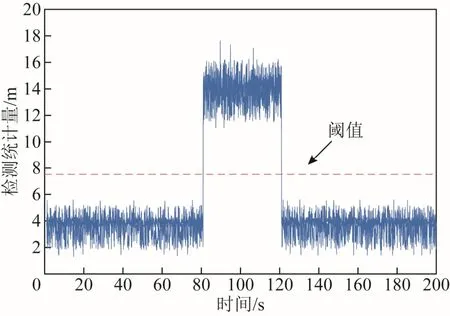
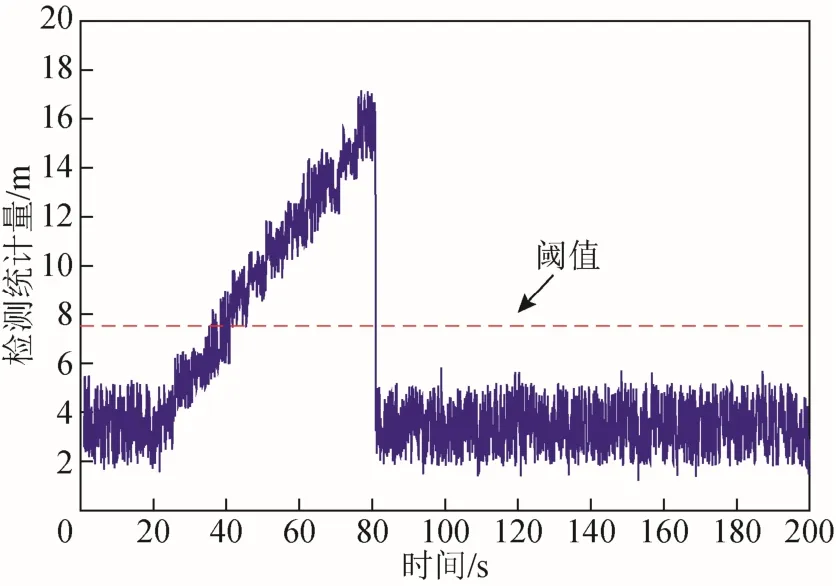
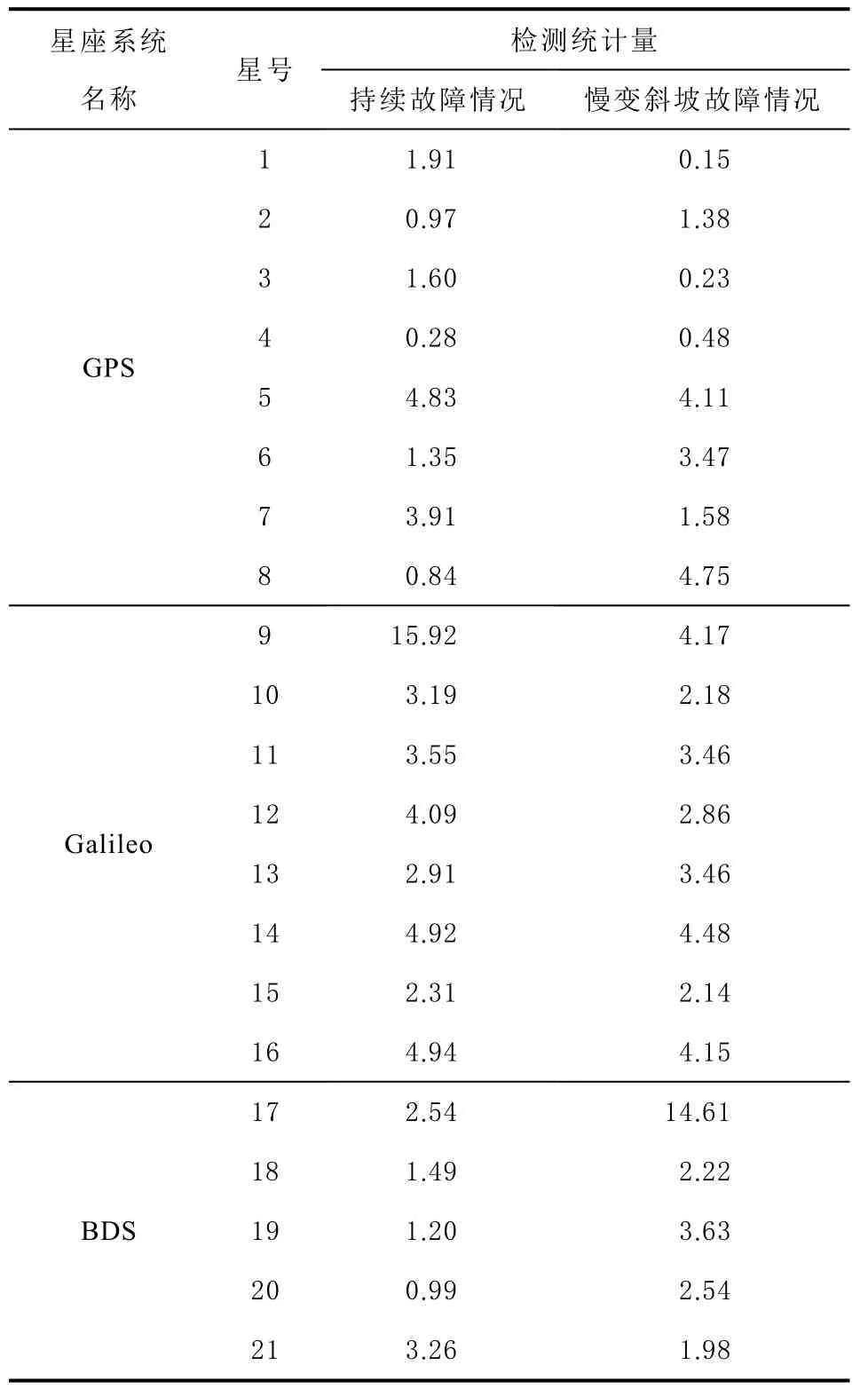
將SHPL與HAL進(jìn)行比較,若SHPL 利用矩陣實(shí)驗(yàn)室(matrix laboratory, MATLAB)軟件對算法進(jìn)行仿真分析,本次實(shí)驗(yàn)選用 GPS、Galileo和BDS三星座系統(tǒng)。首先根據(jù)3個(gè)星座系統(tǒng)的衛(wèi)星及軌道信息參數(shù),對星座進(jìn)行模擬,模擬中選擇24顆GPS衛(wèi)星,24顆Galileo衛(wèi)星和14顆BDS衛(wèi)星,選擇列車用戶位置在青藏鐵路某段線路的固定位置處,用戶觀測衛(wèi)星的高度截至角為15°。 首先對多星座系統(tǒng)和單星座系統(tǒng)下的可見星數(shù)量進(jìn)行仿真對比。圖3為GPS/Galileo/BDS多星座系統(tǒng)與GPS單星座系統(tǒng)在某天同時(shí)刻下可見星數(shù)量的對比情況。由圖3可知,在24 h內(nèi)的任意時(shí)刻,多星座系統(tǒng)的可見星數(shù)量均高于單星座系統(tǒng),由于多星座系統(tǒng)增加了衛(wèi)星數(shù)量,所以在相同路況下,可見星的數(shù)量也隨之增多。隨著可見星數(shù)量增多,更容易滿足 RAIM 算法對冗余觀測信息的需求,在列車運(yùn)行中的某些特殊路段,如城市、山川,多星座 RAIM 能夠更好地保障導(dǎo)航信息的連續(xù)性和完好性。 圖3 可見星數(shù)量對比 圖4為 GPS/Galileo/BDS多星座系統(tǒng)和 GPS單星座系統(tǒng)在 24 h內(nèi)對應(yīng)的位置精度因子(position dilution of precision, PDOP)曲線。 圖4 位置精度因子曲線對比 由圖4可知,多星座系統(tǒng)各時(shí)刻的位置精度因子均小于GPS單星座系統(tǒng),說明多星座系統(tǒng)能夠有效改善可見星幾何分布的情況,進(jìn)而提高算法的可用性。 圖5表示青藏鐵路某段中密度線路在GPS/Galileo/BDS多星座系統(tǒng)和 GPS單星座系統(tǒng)下的SHPL值對比情況。 圖5 SHPL對比 根據(jù)鐵路領(lǐng)域完好性水平要求,中密度線路的水平告警閾值為20 m[17]。由圖5可知,GPS單星座系統(tǒng)SHPL值的波動范圍為11.2~27.0 m,多星座系統(tǒng)SHPL值的波動范圍為6.0~18.7 m,在34 min之后,GPS單星座系統(tǒng)的SHPL開始出現(xiàn)大于水平告警閾值的情況,發(fā)生虛警現(xiàn)象。多星座系統(tǒng)的SHPL值始終小于水平告警閾值,未出現(xiàn)虛警,且在同一時(shí)刻,多星座系統(tǒng)的SHPL值均小于 GPS單星座系統(tǒng),說明列車在相同運(yùn)行路況下,多星座組合RAIM算法的可用性比GPS單星座系統(tǒng)更好。 本次實(shí)驗(yàn)所用數(shù)據(jù)為無故障衛(wèi)星時(shí)的列車定位數(shù)據(jù),需通過人為給衛(wèi)星注入偽距偏差來模擬衛(wèi)星出現(xiàn)故障,進(jìn)而對算法進(jìn)行驗(yàn)證。選用線路數(shù)據(jù)中幾何構(gòu)型較好的21顆無故障可見星,依次編號為1號至21號,其中:1號至8號為GPS衛(wèi)星;9號至16號為Galileo衛(wèi)星;17號至21號為BDS衛(wèi)星。設(shè)定誤警率P= 1 × 1 0?6,漏警率P= 1 × 1 0?6,F(xiàn)AMD假設(shè)各導(dǎo)航系統(tǒng)的偽距觀測噪聲水平相同,取σ0=5 m 。 在第80—120秒的時(shí)間間隔內(nèi),給9號衛(wèi)星注入60 m的持續(xù)故障,其結(jié)果如圖6所示。 圖6 持續(xù)故障檢測 由圖6可知,在第80—120秒的時(shí)間間隔內(nèi),檢測統(tǒng)計(jì)量超出了預(yù)設(shè)閾值,算法檢測出了衛(wèi)星出現(xiàn)持續(xù)偽距偏差。 在第20—80秒的時(shí)間間隔內(nèi),給第17號衛(wèi)星注入0~60 m的慢變斜坡故障,其結(jié)果如圖7所示。 圖7 慢變斜坡故障檢測 由圖7可知,在第32秒時(shí),檢測統(tǒng)計(jì)量超出閾值,檢測到有故障發(fā)生。隨著偽距偏差的增大,檢測統(tǒng)計(jì)量也不斷增大,算法檢測出了衛(wèi)星出現(xiàn)慢變斜坡偽距偏差。 通過故障識別算法得到兩種故障情況下各衛(wèi)星的檢測統(tǒng)計(jì)量如表1所示,檢測統(tǒng)計(jì)量最大的衛(wèi)星即為故障星。 表1 各星座系統(tǒng)衛(wèi)星檢測統(tǒng)計(jì)量的值 由表1可知,在持續(xù)故障情況下,9號衛(wèi)星的檢測統(tǒng)計(jì)量最大,為算法識別出的故障星。在慢變斜坡故障情況下,17號衛(wèi)星的檢測統(tǒng)計(jì)量最大,為算法識別出的故障星。算法有效識別出了在持續(xù)故障和慢變斜坡故障兩種情況下預(yù)設(shè)的故障星。 為檢驗(yàn)多星座 RAIM 算法的檢測性能,利用3.2節(jié)列車定位數(shù)據(jù)對算法的故障檢測率和故障識別率進(jìn)行仿真分析。 給某顆衛(wèi)星注入 0~200 m的偽距偏差,采樣時(shí)間為24 h,采樣間隔1 min,仿真結(jié)果如圖8和圖9所示。 圖8 故障檢測率對比 圖9 故障識別率對比 由仿真結(jié)果可知,當(dāng)偽距偏差達(dá)到100 m時(shí),多星座系統(tǒng)的故障檢測率和故障識別率均可達(dá) 100%,而對于GPS單星座系統(tǒng)當(dāng)偽距偏差達(dá)到136 m時(shí),故障檢測率才達(dá)到100%,偽距偏差達(dá)到160 m時(shí),故障識別率才達(dá)到94.1%。表明多星座組合RAIM的故障檢測性能優(yōu)于GPS單星座RAIM。 本文利用多星座組合RAIM技術(shù),實(shí)時(shí)檢測接收機(jī)自身以及衛(wèi)星故障,進(jìn)而提高列車運(yùn)行過程中定位的精度。在列車定位過程中,采用多星座系統(tǒng)可在相同路況下獲得更多的可見星,從而提高RAIM算法的可用性及信息冗余度。在故障檢測部分,利用奇偶矢量法計(jì)算量少、檢測速度快的優(yōu)勢,可實(shí)現(xiàn)故障衛(wèi)星的快速檢測。結(jié)合青藏鐵路列車定位數(shù)據(jù)分別從算法可用性、故障檢測識別和檢測性能三個(gè)方面進(jìn)行了仿真分析。結(jié)果表明,多星座 RAIM 算法的可用性較單星座系統(tǒng)更好,且能迅速地檢測出定位過程中出現(xiàn)的故障衛(wèi)星,并予以識別。由于信息冗余度的增加,多星座系統(tǒng)的故障檢測率和故障識別率較單星座系統(tǒng)均有所提高,位置精度因子較單星座系統(tǒng)有明顯的降低。多星座RAIM技術(shù)可有效提高列車定位精度,保證鐵路運(yùn)輸行車安全。3 多星座RAIM算法仿真分析
3.1 多星座RAIM算法可用性驗(yàn)證
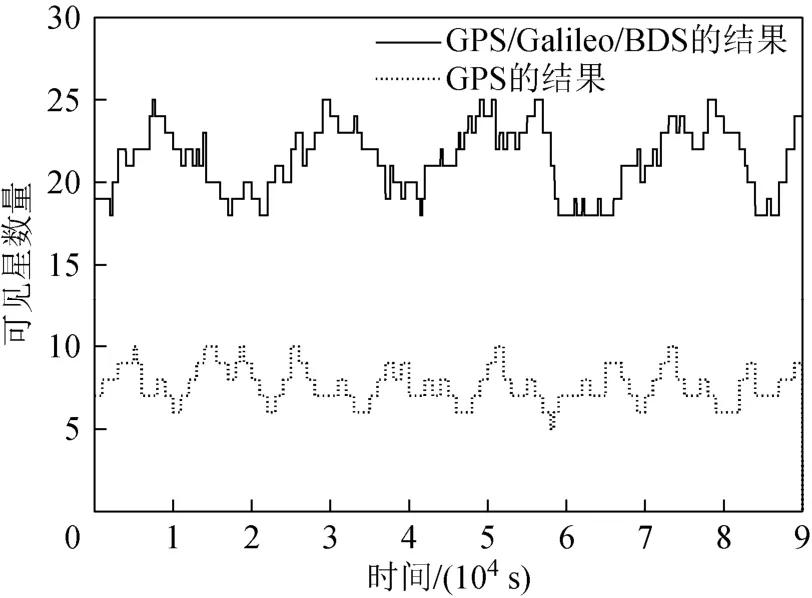
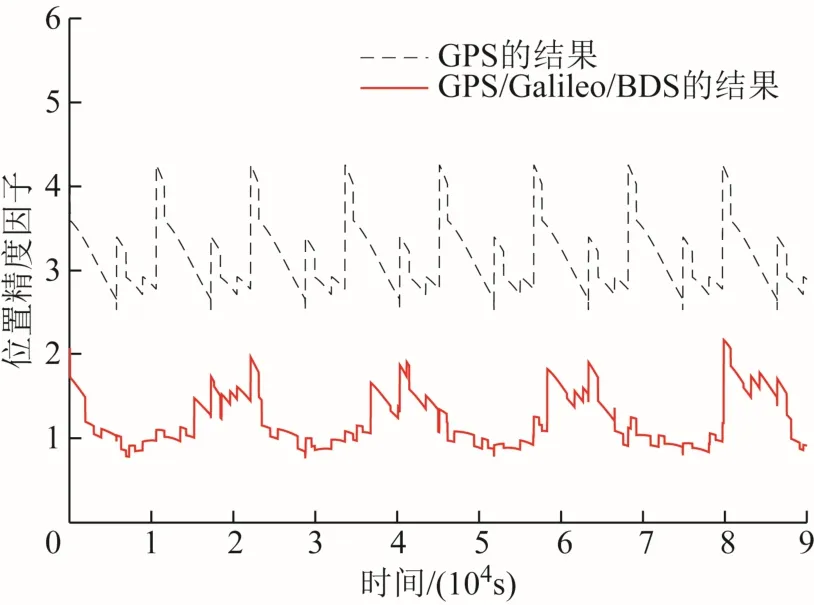
3.2 多星座RAIM算法故障檢測識別
3.3 多星座RAIM算法檢測性能分析
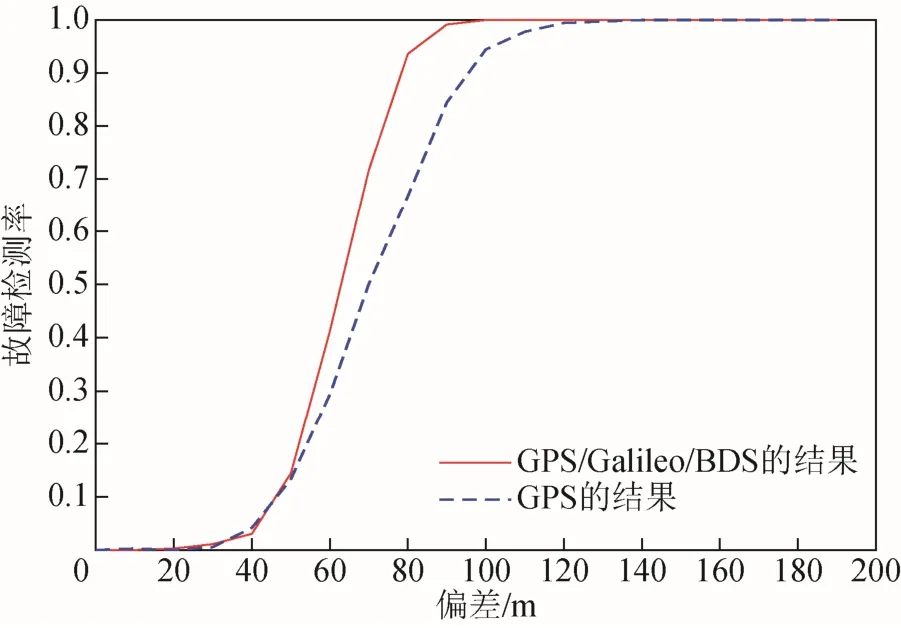
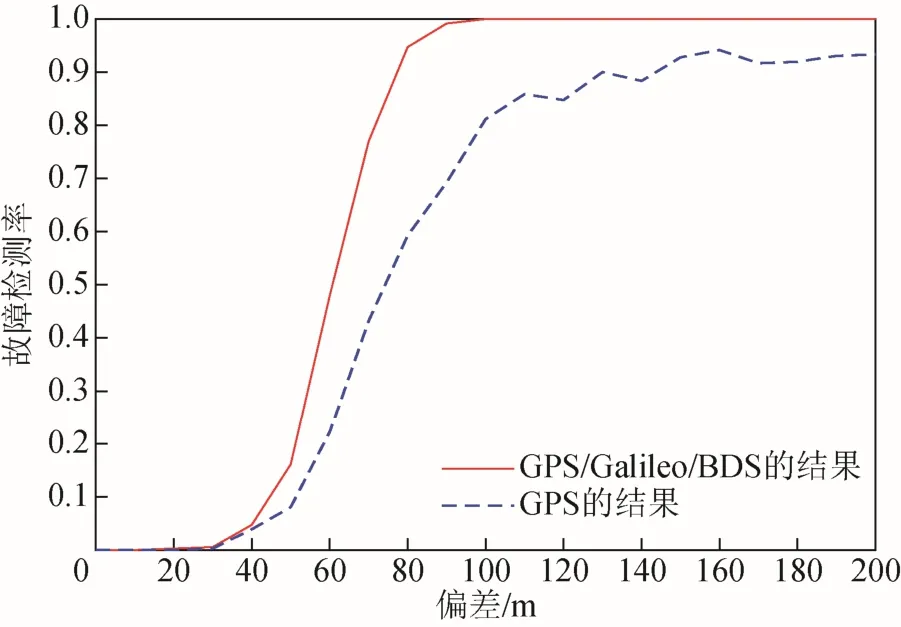
4 結(jié)束語

