清漳河左權縣段防洪治理河道水面線推求

劉鎣鎣

（北京中水利德科技發展有限公司太原分公司，山西 太原 030024）

0 引言

清漳河屬海河流域南運河水系，有東西兩源，清漳東源發源于昔陽縣西寨鄉沾嶺山，清漳西源發源于和順縣西邊八賦嶺，東西兩源在左權縣上交漳村匯合后稱清漳河。清漳河干流經下交漳村入峽谷地段，河道窄而曲折，主流全長210 km，流域面積5 320 km2，其中清漳東源控制流域面積1 586 km2，河長105 km；清漳西源控制流域面積1 568 km2，河長104 km。清漳河山西段流經昔陽縣、和順縣、左權縣和黎城縣，省內流域面積4 150 km2，主流長146 km。左權縣境內的清漳河主要為清漳西源、清漳東源和清漳河干流，清漳西源左權縣境內流域面積1 052 km2。2016年“7.19”洪災是左權縣近20年來所遭受的最大規模洪災，造成全縣水利基礎設施嚴重毀損，清漳河東源最大洪峰流量一度達到800～900 m3/s，多處堤防及道路損壞，使當地居民生命財產面臨嚴重損失和巨大威脅。文章主要研究清漳河左權縣段防洪工程中的關鍵性問題，即不同洪水頻率工況下河道水面線位置，為河道堤防頂高程的確定提供依據。

1 二維水動力數值模型

傳統河道一般應用一維能量方程逐段試算法推求不同斷面水位，這種做法在適用條件和計算過程等方面存在諸多局限，計算結果的可靠性也無法保證。為此，文章應用二維水動力數值模型進行清漳河左權縣段防洪河道多種洪水頻率工況下水面線高程模擬計算，并將計算結果與一維能量方程逐段試算結果進行比較，以保證所分析河段水面線推求結果的準確。在應用二維水動力數值模型進行清漳河左權縣段防洪河道水流流動問題分析及水面線推求時，選擇Poisson 方程進行坐標轉換，力求將物理域內不規則區域轉換為計算域內矩形區域，從而避免不規則邊界離散時可能存在的誤差。曲線坐標系下二維水動力數值模型如下：

1.1 沿水深積分連續方程

1.2 動量方程

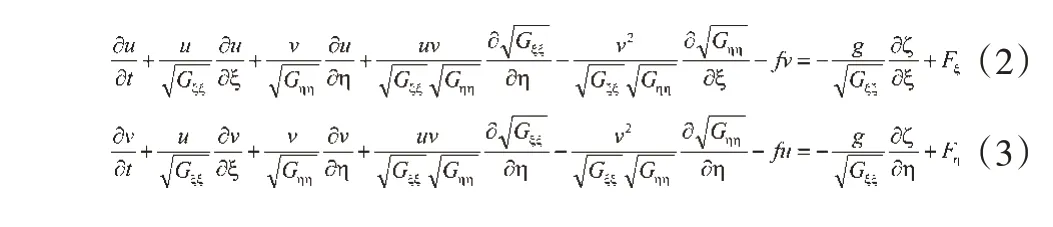
式（1）（2）中：fu、fv —柯氏力系數；fξ、fη— ξ、η向紊動動量通量（kg/s2）；其余參數含義同前。

1.3 定解條件

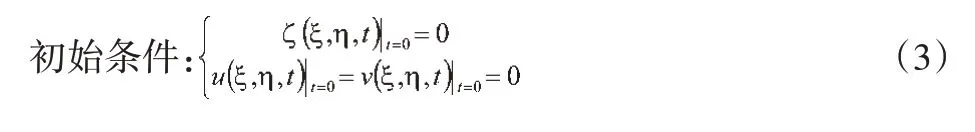
式中字母含義同上。

出入流開邊界上均給定流速、流量及水位過程；固壁邊界則為無滑移邊界。

文中主要采用有限差分法進行數值離散模擬分析，該方法將一個時間步長劃分成兩個時間層，分別包含半個時間步長。每一時間層內的所有項均通過空間上至少存在二階精度的方法求解。這種處理過程精度高、穩定性好，但靈活性差，對于具有混合偏導數的情況并不適用。

2 工程實例

2.1 工程概況

此次河道治理段位于清漳河東源下游段，治理段起點樁號0+000，地處箕山村下游100 m處，終點樁號8+877，位于西黃漳村下游260 m 處，治理段長約8.80 km。此段清漳東源流向為自東北向西南，河谷內常年存在基流。清漳河東源兩岸岸坡陡峭，屬于基巖岸坡，河谷谷底則地勢緩和、地形平坦，河谷寬300～700 m，從上游至下游河床地面高程在920～850 m變化，相對高差達70 m。清漳東源治理段兩岸支溝發育，支溝中常年無水，僅在汛期存在洪水出流現象。本次清漳河東源治理段河床、河漫灘及兩岸岸坡大量分布低液限粉土、礫卵石以及生活和建筑垃圾等人工堆積物，再加上人工采砂，導致當前河道谷底地形坑洼起伏，十分不利于河道行洪。為此必須對此段河道展開疏浚，將河道谷底人工堆積物徹底清除，使河道谷底坡降以及河谷斷面均滿足行洪要求。

2.2 糙率確定

根據河道分段及斷面設置原則，布置清漳河左權縣段水文斷面，并根據2019年10月～2020年8月實測數據，共設置23條橫斷面。根據和順水文站實測糙率～流量關系圖（圖1），當流量超出1 000 m3/s，糙率值在0.025～0.032 之間變化，而當流量在1 000 m3/s以下時，糙率值取值在0.03～0.06范圍內。

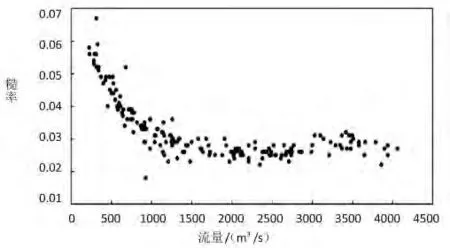
圖1 和順水文站實測糙率～流量關系圖

考慮到清漳河左權縣段河道的復雜性，必須結合河槽沿程變化情況，分河段進行相應糙率值的確定。根據實測枯水位及2020 年洪痕，核定主槽糙率，即根據已確定糙率計算水面曲線，并比較水位計算結果和實際洪痕，如兩者相差較大，則應進行糙率值修正。此外，還應根據現場勘察情況、查表、類似工程經驗等綜合確定灘地糙率值。綜合以上因素，清漳河左權縣段綜合糙率取0.03～0.04，其中主槽糙率和灘地糙率分別取0.02～0.03及0.03～0.05。

2.3 模型建立

清漳河左權縣段計算范圍示意圖詳見圖2所示，該段河道長8.80 km，實測橫斷面23 個，為保證模擬過程中河道地理信息能得到真實反映，采用地形插值法對清漳河左權縣段計算區域內高程散點進行插值以生成地形文件。應用二維水動力數值模型進行洪水計算時考慮兩種工況：工況一為10 年一遇設計洪水；工況二為5年一遇枯水期施工洪水。工況一所得到的洪水位用于堤防和護岸頂高程確定，工況二所得到的枯水位則用于枯水期護岸枯水平臺施工指導。

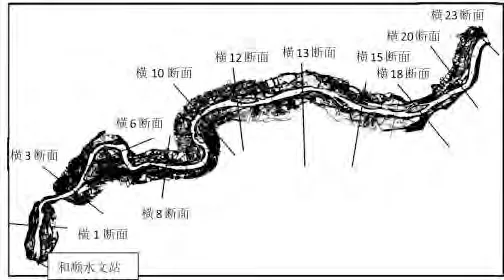
圖2 清漳河左權縣段計算范圍圖

2.4 水面線結果分析

2.4.1 工況一結果

根據清漳河左權縣段河道一維能量方程計算結果和二維水動力數值模擬結果的比較，偏大于0.50 m的斷面占比48%，吻合程度一般。斷面2～3 處主要為束窄的峽谷段，水面比降大，且水面突降現象十分明顯，二維水動力數值模擬結果也略微低于一維能量方程計算結果，差值為0.91 m。斷面7～9間河道存在大角度轉彎，且河床束窄，二維水動力數值模擬結果比一維能量方程計算結果偏大，差值在0.70～1.24 m，兩結果差值最大值出現在斷面8 處。斷面14～21 間存在一處120°左右的彎道，使斷面間水面線突降，二維水動力數值模擬結果比一維能量方程計算結果小0.64～1.45 m，差值最大值出現在斷面16處。結果見圖3。

2.4.2 工況二結果

在該工況下，水面線一維能量方程計算結果和二維水動力數值模擬結果總體較為吻合，偏差在1.50 m以上的斷面數僅占24.50%。河道水位降低后地形的影響程度開始逐漸增大，斷面2和3之間的水面線突降；斷面5和斷面8處一維能量方程計算結果和二維水動力數值模擬結果誤差分別為-0.71m和-0.54 m；斷面14～16間不存在水流上灘，所以二維水動力數值模擬過程中糙率并未出現突然增大現象，一維能量方程計算結果中也不存在水面線突降；斷面18～22之間二維水動力模擬結果均比一維能量方程計算結果大，且所大數值0.46～1.27 m。具體見圖4。

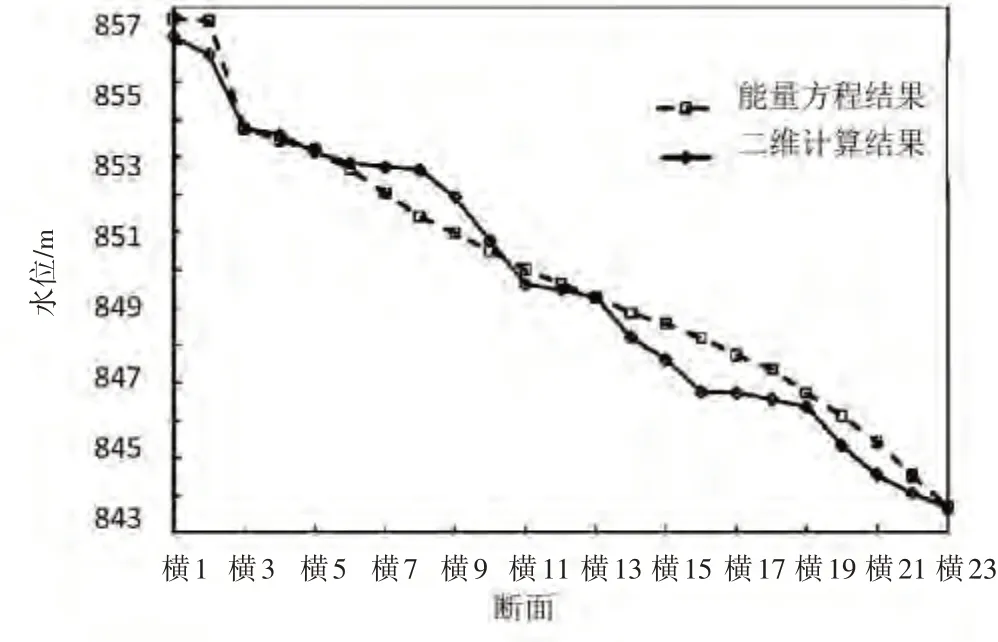
圖3 工況一水面線沿程分布圖

3 結論

采用二維水動力數值模型分別計算清漳河左權縣段防洪治理河道10年一遇設計洪水以及5年一遇枯水期施工洪水工況下水面線高程，可以得出以下結論：一維能量方程是河道水面線計算的基本理論與方法，適用于恒定流，通過逐段試算能基本滿足河道治理工程水面線計算需要，過程簡便易行；二維水動力數值模擬方法則適用于廣闊水域，如用于河流水面線計算，則適用于具有大片灘地的河段，當洪水來臨時灘地水流若不是沿同一方向運動，則應構建二維模型，進行洪水側向流動過程重演。為保證水面線推求結果的準確性，應在相對順直且存在堤防約束的河段使用一維能量方程計算水面線，在局部地形復雜，水流頻繁游移于灘槽變動的河段、無堤防約束的洪水漫流地區，使用二維水動力數值模擬方法進行河道水面線推求。

圖4 工況二水面線沿程分布圖