大尺度風電消納下電力系統發電機組兩階段魯棒優化運行

楊 瑩，孫建宇，董鳳麟，曹美萱，李愛輝

(黑龍江科技大學 電氣與控制工程學院，哈爾濱 150022 )

0 引 言

為了達到碳達峰、碳中和目標，國家能源局提出積極推動新能源發電項目“能并盡并，多發滿發”要求。但是風光可再生能源具有周期性和隨機波動性，發電功率難以準確預測。同時網側火電機組運行本身存在著大慣性及出力區間限制的因素。因此，對于可再生能源的大尺度有效并網消納是亟需解決的難點問題。

風電大尺度接入的電力系統優化問題實質上是對供電系統中發電機組發電功率進行相關優化的問題。文獻[1]考慮了風電大規模接入電力系統的情況，為此提出了深度調峰的概念。由于考慮到機組本身的一些物理特性的限制，使得發電機在某些區域內軸承震動變大，為此在傳統電力系統經濟調度模型中設置了發電機運行的禁止區間[2]。除此之外，由于機組在啟停調峰過程中會對機組壽命產生一定的影響[3-4]，文獻[5]考慮了這一影響，建立了考慮降低機組壽命的機組組合規劃模型，但是此模型中的約束具有非線性的特點。文獻[6]引入了不確定場景集合來表示風電出力的不確定性，構建出了min-max-min三層兩階段模型來獲取最嚴重場景下機組最小的經濟花費，并且采用列約束生成算法(column and constraint generation，C&CG)[7]算法求解該模型。文獻[8]建立了考慮風電爬坡時間約束的精確線性化模型，并提出了使用風電預測值及其區間預測上下限來描述風電場出力的方法，從而利用魯棒優化理論將此隨機問題轉化為確定性問題后進行求解。在考慮到風電大規模完全接入的情況下，考慮風電的實時波動性，采用實時調度的方案可能會導致發電機組的發電量發生突變，因此有必要對機組采用日前調度的調度方案。

針對風電可再生能源發電功率難以預測，并網時風力發電功率存在超出預測范圍情況，導致風電大尺度消納時網側火力機組存在的安全運行隱患和使用安全壽命問題，考慮機組爬坡、禁運區間、機組啟停、安全容量因素，建立運行優化模型，使系統在滿足風電能并盡并的同時提升系統的安全性和經濟性。利用NC&CG算法求解了所建兩階段魯棒機組運行模型。

1 大尺度風電并網消納問題

某風電場數據曲線如圖1所示。

圖1 典型日場景分析

運行中存在2個典型場景:場景1為第3 h到第9 h，在此場景下電負荷基本維持不變，風力發電出現強烈下降波動；場景2為第11 h到第15 h，同樣電負荷基本保持穩定，風力發電出現較強上升波動。針對這2種場景，現有風電并網手段是棄風或利用儲能調節手段保持功率穩定。但是，由于儲能設備的成本因素，現階段大規模儲能電廠尚處于實驗階段，因此，大尺度的風電并網消納仍主要需要借助火電機組調峰實現。限于火電機組本身的大慣性特性和風力發電的精確預測問題的矛盾，在實現“應并盡并，能發盡發”過程中，會給機組安全經濟運行帶來嚴重隱患。

圖2 機組禁止運行區間

2 建立系統優化模型

2.1 多目標函數模型

采用兩階段魯棒優化建模方法，在第一階段建立機組啟停安全經濟模型，第二階段在風電預測不確定情況下，建立火電機組分段出力經濟模型，模型如式(1)、(2)所示。

(1)

(2)

式中：Ii,t為0-1變量，表示機組運行狀態；Fi為機組最小運行費用；FUi,t為機組開機費用；FDi,t為機組關機費用；FLi,t為因影響機組壽命而造成的經濟損失；Fost為機組發電費用；Fgi,p為機組在p分段的發電費用；PG,i,t,p為機組在p分段的發電功率；NG為火電機組集合；T為調度周期。

2.2 大尺度消納下機組爬坡速率約束

可再生能源本身存在的特性使得風力發電功率難以準確預測，為了在大尺度風電并網消納時減小對機組的沖擊影響，采用柔性調度方案，如圖3所示。

(3)

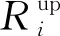
(4)

式中：ui,t為新引入的0-1變量。

2.3 機組禁運區間約束描述

在風電并網消納場景下，考慮機組禁運區間限制對于系統安全穩定運行是十分必要的。根據現場運行規范要求，限制各發電機組出力范圍及各機組子區間輸出功率限制。建立禁止區間線性化約束，如式(5)～(7)所示[9]：

(5)

式中：zi,t,q為第q運行分段內機組的運行狀態。

(6)

(7)

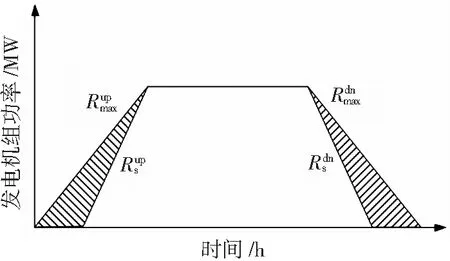
圖3 機組壽命損耗區間

2.4 機組最小啟停時間約束

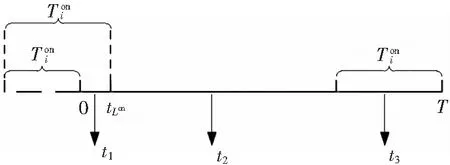
圖4 各時間量關系圖

mi,t+ni,t≤1

(8)

(9)

式中：mi,t為0-1變量，值為1時代表機組開機；ni,t為0-1變量，值為1時代表機組關機;Ii,0為機組初始狀態。

(10)

(11)

(12)

(13)

(14)

(15)

2.5 電力系統約束

在電力系統建模方面考慮負荷平衡約束如式(16)所示：

(16)

式中：NG為發電機集合；NW為風電場集合；NB為負荷集合；PG,i,t為發電機組發電功率；PB,i,t為系統負荷功率；PW,i,t為風電機組發電功率。

此外，考慮線路本身具有不同的安全容量,建立線路安全容量約束如式(17)所示：

?b,?t

(17)

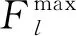
2.6 風電預測不確定性約束

考慮風電出力預測不確定性，采用了區間預測的方式對于風電的出力區間進行了描述，其風電出力區間為式(18)所示。根據相關理論[10-11]，結合所提模型，可以得出以下結論：風電的波動性對電力系統機組調度規劃影響最大的場景一般是風電場出力最大或者最小的時刻。因此，對式(18)進行改進建立式(19)，以達到更快的求解速率：

(18)

Φ:{PW,i,t∈RNW×T:PW,i,t=

(19)

式中：β為新引入的0-1變量。

以上建立的三層兩階段魯棒優化模型是一個混合整定規劃(mixed-Integer linear programming，MILP)問題。從結構上來講，包含了外層、中間層與內層三層模型，外層模型約束中主要包含了機組啟停的相關模型約束，中間層模型約束中主要包含風電場不確定性模型約束，內層模型約束中主要包含電力系統相關的模型約束。

3 三層兩階段模型求解算法

所建三層兩階段模型是一個MILP模型，約束均為線性約束，對于普通的MILP可以很好地利用CPLEX、GUROBI等商業求解器進行快速求解。但是對于三層兩階段模型，目前沒有合適的求解器對其進行直接求解。并且由于在內層模型中，包含了0-1整數變量，使模型具有非凸特性，無法通過KKT條件將其直接轉化為單層模型進行求解。因此，采用NC&CG算法進行求解，此算法本質上是兩層C&CG算法的循環。

為了便于表示，首先將模型簡寫為式(20)，其中：D·Io≤h1代表了外層模型中的式(8)～(15)；X1·Io+Q1·Iu+Y1·P=E1·u與X1·Io+Q1·Iu+Y1·P≤E1·u代表了內層與中間層的等式以及不等式約束，包括了式(3)～(7)以及式(16)～(19)。

(20)

式中：Io為第一階段的0-1變量Ii,t，mi,t,ni,t與ui,t；Iu為內層的0-1變量zi,q,t；P為內層的連續型變量PG,i,t與PG,i,q,t；u為中間層變量PW,i,t；D1、D2、Q1、Q2、Y1、Y2、h21、h22為系數矩陣；h1、h2為常數項矩陣。

利用NC&CG算法中的相關理論，可以寫出式(20)的外層主問題式(21)，此問題為一個MILP問題，可調用求解器進行求解，求解后有LBout=AT·Io*+η*,其中LBout為外層問題的下界。

(21)

式中：Iu,r為第r次外層循環中產生的內層0-1變量；Pr為第r次外層循環中產生的內層連續型變量；ur為第r次外層循環中產生的。

在以上模型的求解過程中，主要涉及雙層模型的轉換以及NC&CG算法的使用，具體過程如下。

3.1 雙層模型的轉換

在目前研究中，對于雙層問題的處理一般是使用KKT條件或者強對偶理論(strong dual theory，SDT)將雙層問題轉換為單層問題，然后利用求解器對其進行求解。而對于該文模型中來說，由于內層存在0-1，需要先賦給內層中的Iu變量一個初值，得到了式(22)，使內層問題成為一個凸優化問題。

(22)

可以利用KKT條件對式(22)進行轉化。首先，提取出內層模型，由于KKT條件只對原模型中的不等式約束進行處理，所以提取的內層模型如式(23)所示：

(23)

然后，構建式(23)的拉格朗日式(24)。其KKT條件共有4個，如式(25)所示。最后，結合內層模型便可以寫出被替換后的單層模型，如式(26)所示。

L(P,u)=BT·P+

[X1·Io+Q1·Iu+Y1·P+h21-E1·u]λ1+

[X2·Io+Q2·Iu+Y2·P+h22-E2·u]λ2

(24)

(25)

(26)

然而，最終得到的式(26)中含有互補松弛約束，其為[X·I*+Q·Iu,o*+Y·P+h2-E·u]·λo=0，顯然此約束中包含著雙線性項。目前，通常采用大M法(Big-M Method)來對此類約束問題進行處理，處理之后得到式(27)。式(26)中Y=[Y1;Y2]，λ=[λ1;λ2]；Iu,e與Pe為第e次迭代中引入的變量，R為總的迭代次數。

(27)

至此，雙層模型已經轉化為一個MILP的單層模型，可以調用求解器對其進行求解，求解之后獲得UBin=τ，其中UBin為內層問題的上界值。

3.2 NC&CG算法

NC&CG[12]是為了求解文中所提的內層含有0-1變量的模型而設計的算法。三層兩階段模型在使用C&CG算法后會被轉化為一個主問題以及一個子問題，而NC&CG算法將內層子問題進行了進一步處理，又嵌套了一個C&CG算法，以此來實現對于內層中0-1變量的處理。根據NC&CG中的相關理論，提出了內層下界子問題式(28).值得注意的是，式(28)與式(23)是存在不同的，體現在內層變量Iu上，在式(23)中Iu*為一個給定的初值量，在式(28)中Iu是一個0-1變量，求解之后獲得LBin=min{LBin,BT·P},其中LBin為內層問題的下界值。

(28)

至此，NC&CG算法中用到的3個子問題已全部列寫完畢，所用的NC&CG算法的具體流程圖如圖5所示,圖中UBout為外層問題的上界值。

圖5 NC&CG算法流程圖

4 仿真分析

在Matlab中利用Yalmip工具箱進行上述模型的搭建，并調用Gurobi求解器對其進行求解，所用Gurobi版本為9.1.1，測試系統的硬件環境為i5-10400f(2.9 GHz)，內存為16 GB。測試用節點系統為改進的6節點系統，如圖6所示。

圖6中，包含了3臺火電機組，裝機容量分別為200 MW，150 MW與180 MW；在節點2與節點5上分別設置了2個風電場，其風電出力預測值如圖7所示；母線2、母線4以及母線5的位置處設置了3個負荷，其占總負荷的比例分別為30%、30%與40%，系統總負荷預測曲線如圖8所示。設置了機組的禁止運行區間分別為[100,140]、[75,105]、[90,126]。以考慮機組安全爬坡約束以及不考慮機組安全爬坡約束2種調度場景進行仿真驗證。

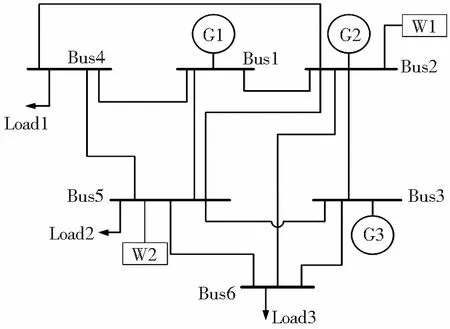
圖6 改進的IEEE6節點系統

圖7 風電場發電功率預測曲線

圖8 負荷功率預測曲線

為了分析機組安全壽命損耗爬坡約束對電力系統機組調度運行產生的影響，設置了2個場景如下：

案例1：未考慮機組安全壽命損耗爬坡約束的電力系統機組經濟調度。

案例2：在場景1的基礎上考慮了機組安全壽命損耗爬坡約束。

如圖9所示，為案例1與案例2下系統機組總開機狀態的區別，可見為了確保系統內機組的總體安全性，在案例2下系統內機組開機數量變多。其具體出力情況如圖10所示。

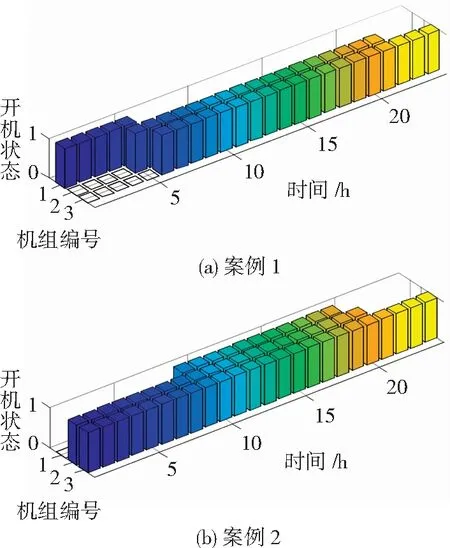
圖9 機組開機狀態

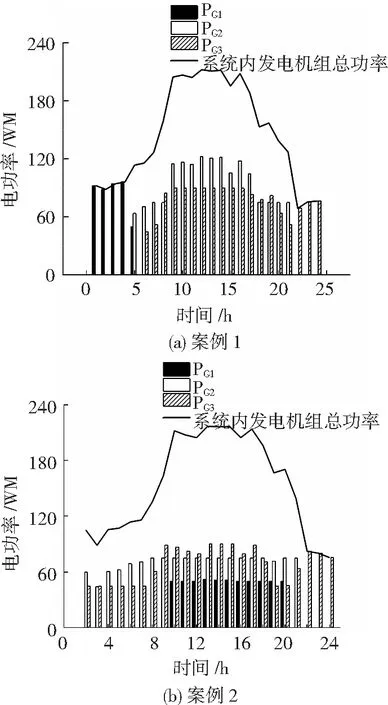
圖10 機組各發電功率及系統內全部機組發電功率

圖10中，圖10(a)與圖10(b)分別為在案例1以及案例2下各機組發出電功率以及系統內全部機組總體發出電功率情況。可見在案例1以及案例2下，隨著2個場的風電出力不斷減少，圖10中的系統內機組總發電功率曲線出現了明顯的上升趨勢。由于考慮了風電“應并盡并，能發盡發”的并網政策，風電的強波動性對于整個電力系統來說具有較大的沖擊性，因此在圖10(b)中供電系統呈現出多機組低功率的運行模式，很明顯，比起圖10(a)來說，圖10(b)的機組出力變化更加平滑，大大改善了供電機組安全性。表1給出了案例1以及案例2下各個機組在一個完整的系統調度周期內達到機組壽命損耗區間的次數。可見，通過引入機組安全壽命損耗爬坡約束,改善了機組壽命受損的情況。

表1 機組爬坡速率達到壽命損耗區間次數

案例2下，雖然機組的直接運行成本要高于案例1下機組的運行成本，但是當考慮到機組安全壽命損耗所帶來的長遠經濟成本后，案例2下的運行方式的合理性更加明顯。總之，該結果證明：在考慮大尺度風電消納下，針對風電預測不準確性的特點，所提的三層兩階段模型能夠對于機組進行有效的日前調度優化，以此來實現機組運行的經濟性與安全性。

由上文模型求解部分可知，在處理完所提模型非凸性之后，所剩的一個主要問題便是對雙層模型進行求解。除所提算法，還有Benders分解法可用于該問題的處理，表2給出了使用這2種算法在案例1以及案例2各自模型下的表現，結果表明，在處理所建模型時，所提算法具有更快的求解速度。

表2 2種算法在不同算例下的表現

5 結 語

針對風電大尺度消納時網側火力機組存在的安全運行隱患和使用壽命損耗問題，采用兩階段魯棒優化建模方法，在第一階段建立機組啟停安全經濟模型，在第二階段建立風電預測不確定情況下，火電機組分段出力經濟模型。利用NC&CG尋優算法解決模型非凸特性，尋優結果表明，所建模型有利于大尺度風力發電并網消納時，在實現“應并盡并，能發盡發”目標的同時提高機組運行的安全性與經濟性。