基于小信號電路的虛擬同步發電機控制策略

相東昊，薛 易，閆 旭，陳 元，張 帥

(1.國網東營供電公司，山東 東營 257000；2.黑龍江科技大學 電氣與控制工程學院，哈爾濱 150022；3. 國網淳安縣供電公司，杭州 311700)

0 引 言

隨著分布式發電的快速發展和并網，分布式發電也暴露出其特有的問題，增加了電網控制難度。逆變器是分布式電源接入電網的主要設備[1]，這種直接接入電網的方式會產生一系列的問題，如：產生大量諧波，造成三相不平衡；其利用受到氣象因素的影響，無法保證穩定的電能輸出，無法實現單獨給固定負荷供電，造成無功功率和電壓質量問題。放射狀是大多集中配電網的主要分布形式，電網工作在穩態時，電壓沿電力線路方向逐漸降低[1-3]。逆變器接入電網后，電力線路上流動的功率會減少，使得各負荷節點處的電壓沿電力線路升高，會導致這些負荷節點處電壓不滿足要求，接入電網逆變器的位置和容量會影響這些節點電壓變化的多寡[4-6]。

微網逆變器參與電網調節較為困難，因為其缺乏一定慣性且響應快，使得其無法提供一定的電壓和頻率支撐，更不可能為微電網增加阻尼作用，或者說以上原因導致其無法與微網同步。針對上述原因，一些專家根據發電機對電網具有天然友好特性，提出虛擬同步發電機(virtual synchronous generator ,VSG)控制策略，讓微網逆變器具備發電機的特性以加強微網運行的穩定性，使得儲能系統無論在計劃性還是非計劃性孤島情形下皆能無縫切換，最大限度保護重要負載正常工作。但是由于其數學模型是一個二階系統，存在一對靠近虛軸的極點(即存在)，當對系統相關核心參數整定不合理，可能將導致控制系統效果差且嚴重時系統震蕩發散。當前許多學者對其參數整定提供了一系列解決方案，但由于各自應用情景及現場不一樣，導致系統大打折扣[7-10]。

該文基于小信號電路對其主電路功率環進行設計，并建立其小信號電路模型。針對虛擬同步機功率環相互耦合參數整定難的問題，提出一種不增加線路阻抗的環路解耦控制，并在此基礎上分別對功率環路參數進行定量分析和設計。為了解決無功功率分配不均勻的問題，該文加入負載電壓負反饋控制環節，以此減小負載電壓波動。

1 虛擬同步發電機的基本原理和小信號數學模型

1.1 虛擬同步發電機的主電路

VSG的基本原理是模擬同步發電機的工作特性，使得微網逆變器具有發電機的特點。在研究虛擬同步發電機之前，先來介紹其主電路，如圖1所示。在圖1中，eabc=[ea，eb，ec]T，uabc=[ua，ub，uc]T，iabc=[ia，ib，ic]T，分別為虛擬同步發電機的感應電動勢(橋臂中點電壓)列向量、輸出電壓列向量和并網電流列向量；Zs=Rs+jωLs為VSG的電樞電阻和同步電感；Pe、Qe為VSG輸出的有功功率和無功功率，uC,abc=[uCa，uCb，uCc]T為電容電壓列向量；Z為本地負載。

圖1 虛擬同步發電機主電路

圖2為功率環控制框圖，從圖2中可以看出，逆變器三相信號調制波eam、ebm和ecm是由兩部分組成的：一部分，VSG調制波的頻率和相角是由其有功功率環輸出構成；另一部分，VSG調制波的大小是由其無功功率環輸出構成。在有功環中，Pset為有功功率給定值，Pe為VSG輸出有功功率，ω為其角頻率，ωr是額定角頻率，DP為有功-頻率下垂阻尼系數，K為無功調節系數，同理無功環中的參數有對應的含義。

圖2 功率環控制框圖

1.2 虛擬同步發電機的工頻小信號模型

假設在半個工頻周期(0.01 s)內，有功功率瞬時值和無功功率瞬時值與其平均值相等，事實上這種假設也不會引起較大的誤差，即

(1)

(2)

式中:〈Pe〉Tr/2為半個工頻周期里瞬時有功均值；〈Qe〉Tr/2為半個工頻周期里瞬時無功均值；T1為工頻周期。

VSG控制結構的狀態方程為

(3)

式中：δ為功角；J為虛擬轉功慣量；Xs為發電機同步電抗；KPWM為傳遞函數；Ur為網側額定電壓的幅值;Uo為VSG輸出電壓的幅值；Uin為輸入電壓；Utri為三角載波的幅值。其中，式(3)中后兩個式子是虛擬同步發電機發出有功功率和無功功率經過1/2個周期均化后的算式，只不過這兩個算式與穩態時輸出功率表達式相同。

將式(3)中狀態量寫為兩部分之和，即

(4)

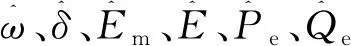
(5)

令工頻下無功下垂阻尼系數DQ1=UinDQ/(2Utri)，對式(5)進行拉式變換，有

(6)

根據式(6)，可以得到虛擬同步發電機在拉普拉斯域內的工頻小信號模型，如圖3所示。

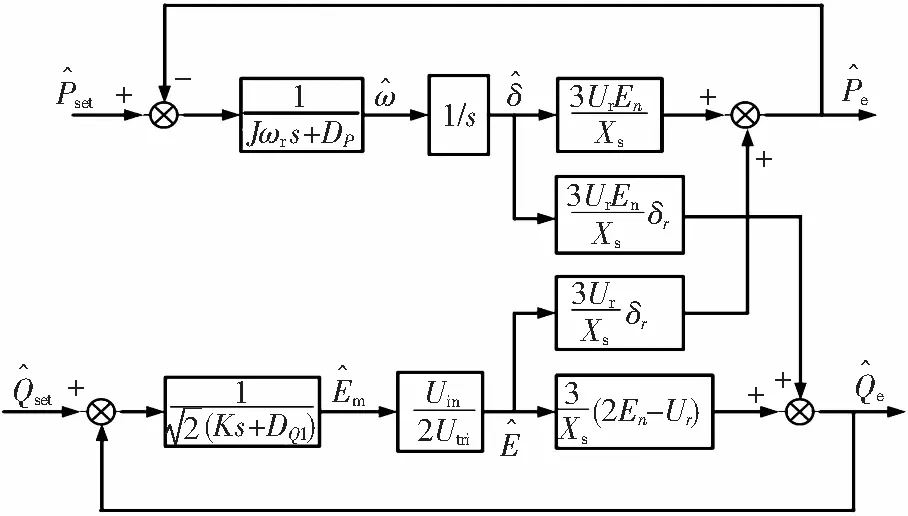
圖3 功率環控制框圖

由圖3可以看出，無功功率環和有功功率環耦合在一起。為了不至于使控制系統過于復雜，必須讓有功和無功解耦。

2 虛擬同步發電機控制及其參數設計

2.1 功率環解耦設計

前面分析功率耦合會對控制穩定性產生不利影響，所以要通過功率解耦的方式來改善控制系統穩定性。該文通過在虛擬同步發電機控制回路加入交叉前饋補償環節來減輕虛擬同步機有功功率、無功功率耦合對控制系統的影響，其解耦后的功率控制框圖如圖4所示。在圖4中，有功功率擾動和無功功率波動的交叉前饋補償系數分別為KP、KQ，其中Gm，P(s)為虛擬發電機轉子機械方程的傳遞函數，具體表達式如下：

(7)

(8)

(9)

(10)

(11)

(12)

式中:HP，δ(s)、HQ，δ(s)、HP，E(s)、HQ，E(s)為解耦功率環的傳遞函數。

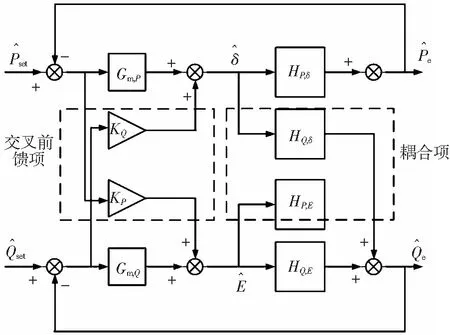
圖4 解耦的功率環控制框圖

(13)

KQ的表達式容易寫出

(14)

式中：KQ為無功前饋補償系數。

(15)

KP的表達式容易寫出

(16)

式中：KP為有功前饋補償系數。

式(14)、(16)分別給出了無功和有功前饋補償系數KQ、KP的具體式子，為有效減小有功功率某一瞬間產生波動對VSG的頻率和功率角的干擾，虛擬同步發電機控制的截止頻率不應超過基波頻率的1/5。補償系數可以根據式(14)、(16)在10 Hz內的相頻域和幅頻域整定。

則解耦后的有功功率環路和無功功率環路增益TP(s)和TQ(s)即為

(17)

2.1.1 虛擬同步發電機有功功率環路參數設計

從式(17)可以看到，由比例單元3UrEn/(XsDP)、積分單元1/s和一階低通濾波單元1/[(Jωr/DP)s+1]這3個基本環節組成有功功率環路增益。其中，有功功率環路的開環放大倍數取決于DP，而一階低通濾波單元的轉折頻率fL,P取決于轉動慣量J和DP，其表達式如下：

(18)

式中，fL,P為有功功率環路的轉折頻率。

從上面分析可以知道，如要設計好有功功率環路的參數設計，那么就要處理好有功-頻率下垂系數DP和轉動慣量J，然而有功頻率下垂系數是由國家標準規定的，故需要通過整定轉動慣量J以使該環路符合運行穩定性和動態響應的要求。在有功功率回路的截止頻率fc,P處，系統回路放大系數的幅值等于1，根據式(17)可得

(19)

求解式(19)，解得

(20)

為了確保式(20)有解，那么要確保式(20)中二次根式內的表達式非負，要求

(21)

式中:fc,P為有功功率環路的截止頻率。

當截止頻率取最大值fc,P=fc,P,max時，由式(20)解得轉動慣量J=0。該結果的物理含義是顯而易見的：相同頻率，轉動慣量越小，則一階低通濾波單元1/[(Jωr/DP)s+1]的幅值越高；當不存在慣性時，即J=0，則一階低通濾波單元1/[(Jωr/DP)s+1]簡化為單位放大單元，此時對應的截止頻率也是最大截止頻率。但如果轉動慣量為0，那么VSG就沒有存在的意義，即要求J>0，因此必須保證fc,P

為了使系統有充分相位裕度PMreq，則要求

PM=180°+∠TP(j2πfc,P)≥PMreq

(22)

式中:PM為相角裕度；PMreq為系統相角裕度。

將式(17)的第一個式子代入式(22)，通過計算得到

(23)

對式(23)兩側一起作反三角變換，可以求解得

(24)

從式(24)中可以看出，轉動慣量J并不是沒有上限的，它決定于系統相位裕度PMreq。這個結論的物理意義也是顯而易見的，觀察式(20)可知，有功頻率下垂系數DP越大，那么轉動慣量J就越大，又由式(18)可知，J在分母上，則一階低通濾波單元的轉折頻率fL,P勢必越小，就會導致截止頻率fc,P也會隨著轉折頻率的降低而產生更大的滯后角，系統留有的裕度PMreq也就會越低。故為了使系統相角裕度達到要求，轉動慣量J不要取過高。綜上所述，轉動慣量式J既不能取0，也不能取得過大。

為了直觀表示轉動慣量J與截止頻率之間fc,P的聯系，由式(20)可以繪出它們之間的關聯曲線(用藍線表示)，如圖5所示。要想確定轉動慣量J和截止頻率fc,P之間的具體關系，還需要根據式(20)畫出由相角裕度確定的邊界線(用紅線表示)，邊界線和關系曲線兩者的交點所對應的頻率即為符合相角裕度要求的最小截止頻率fc,P,min。通過式(21)可知，截止頻率是有上限的，則可以確定截止頻率fc,P的上下區間了。

從圖5中可以看出，轉動慣量J和截止頻率fc,P之間是單一映射關系，這樣也就確定轉動慣量J的取值范圍，在圖5中用實線框表示出來。

圖5 轉動慣量與截止頻率的選擇區域

2.1.2 虛擬同步發電機無功功率環路參數設計

(25)

式中:fL,Q為無功環轉折頻率。

在設計無功功率環路參數時，與有功功率環路參數也有很大的相似之處。根據上面分析可知，只要整定好無功-下垂系數DQ1和慣性系數K，那么就能獲得無功功率環路增益。同樣，下垂系數DQ1是要符合國家規定標準的，因此只要處理好慣性系數K就能使系統滿足穩定運行和動態特性的要求。鑒于無功功率環路中的一階低通濾波單元在截止頻率fc,Q處最大發生負90°偏移，由此可以推斷無功功率環路最低相角裕度PM為90°，故在該環路中相角裕度必定符合系統要求的，那么現在只需通過在截止頻率fc,Q處無功功率回路放大系數大小為1的等式關系就可得到慣性系數K。由式(17)的第二個式子便可得到無功功率環路增益在截止頻率處的幅值，關系式如下：

(26)

式中，fc,Q為無功環截止頻率。

反解式(26)，即可得到

(27)

式中:K為慣性系數。

對于式(27)，下面分兩種情況來進行分析：

第一種情況有解時，根號內表達式計算結果為正數，那么可通過式(27)解出慣量系數K。值得一提的是，VSG輸出電壓會受到瞬時無功功率中兩倍工頻擾動量的干擾，為了減小這種干擾，無功功率回路的截止頻率fc,P常常在兩倍工頻的1/10以內進行選擇。

第二種情況無解時，二次根式內表達式計算結果為負數，那說明無功功率環路的截止頻率不存在，其回路放大倍數在整個頻段內最大值為0 dB。為了使兩倍工頻擾動量不至于對無功功率環路造成較大影響，無功功率環路中的一階低通濾波單元的轉折頻率fL,Q常常在兩倍工頻的1/10以內進行選擇。由式(25)得

(28)

式中:f1為工頻。

對式(28)作進一步整理可求得

(29)

2.2 VSG并聯改進策略

當虛擬阻抗發電機的傳輸阻抗呈現純感性時，則可實現有功功率與無功功率的有效分離。在穩態運行時，有功功率基本可以實現均分，而無功功率的分配受到無功-電壓下垂特性以及功率參考值和傳輸阻抗等多因素的影響，這就決定了無功功率分配難度要大于有功功率分配。與此同時，負載電壓波動還受到負荷波動和無功-電壓下垂特性的影響。為了解決無功功率分配不均勻的問題，加入負載電壓負反饋控制單元Ku(Ur-UL)，來緩解負載電壓變化，使得VSG輸出電壓能夠滿足系統電壓質量的要求，其中Ku為電壓反饋系數。然后在無功-電壓環中構造積分環節，使得在穩態時傳輸阻抗能與無功功率充分解耦，無功-電壓改進控制策略如圖6所示。

圖6 無功-電壓改進控制框圖

系統正常運行時，積分單元沒有輸入(即輸入為零)，微網逆變器等效輸出阻抗會因積分單元而改變，有

DQ(Qset-Qin)=Ku(UL-Ur)

(30)

從以往電力系統運行經驗可知，等效輸出阻抗遠遠大于線路阻抗，這時如果增加負載電壓負反饋和積分環節且保證輸出電壓在一定范圍內，那么就可以實現無功功率與傳輸阻抗的充分解耦。這時只需保證電壓反饋系數Ku相等，無功功率參考值及下垂系數按照VSG的額定容量進行設計，就能實現無功功率的準確分配。

3 仿真分析

仿真時間為8 s，仿真步長為2×10-6s，逆變器的基準容量為20 kVA，整個系統進行標幺化，電網側電壓有效值為380 V，線路等值阻抗(標幺值)設為Z=0.26+j1.570 7，斷路器的頻率為10 kHz，濾波電容為25 μF，直流側電壓為700 V，網側額定相電壓有效值為220 V，電流環系數為2，濾波電感為2 mH，濾波電容為25 μF，額定工作頻率50 Hz，無功環比例與積分系數分別為0.05、5。

根據前面功率環參數設計分析，分別選取J靠近工頻50 Hz和遠離工頻50 Hz的值，從圖7可以看到，選取靠近工頻J存在功率和電流震蕩，而遠離工頻J參數電流和功率沒震蕩且穩定，這和上述分析一樣，從而校驗了功率環設計方法的正確性和有效性。

圖7 靠近/遠離工頻的功率和電流波形

傳統策略2臺VSG并聯功率波形如圖8(a)所示，從圖中可以看出，由于線路阻抗不同，導致傳統策略下2臺VSG并聯輸出有功功率無法均分，從而使得有功功率調整需要一定的時間。改進后的2臺VSG并聯輸出有功功率如圖8(b)所示，通過改進VSG并聯策略，使得2臺VSG輸出有功功率有效均分，更容易滿足本地負荷要求，減小有功功率頻繁波動。

圖8 兩種控制策略并聯功率對比

傳統控制策略下2臺VSG并聯產生的環流如圖9(a)所示，從圖中可以看到，傳統控制策略下由于2臺虛擬同步發電機發出電壓的大小與相位差異較大，以及虛擬同步控制策略參數差異還有主電路的非線性，在并聯時極易產生較大的環流。

通過引入負載電壓負反饋調節環節和SSRF-PLL鎖相技術使得VSG輸出電壓大小和相位接近一致，從而減小系統中的環流，減小了Ih環流見圖9，對并網逆變器的沖擊，改進后2臺VSG并聯時產生的環流如圖9(b)所示。

圖9 兩種控制策略環流對比

4 結 語

采用基于小信號電路對虛擬同步機主電路功率環進行了設計，并建立其小信號分析模型。針對虛擬同步機功率環相互耦合參數整定難的問題，提出一種不增加線路阻抗的環路解耦控制，并在此基礎上分別對功率環路參數進行定量分析和設計。同時針對無功功率分配不均勻的問題，加入負載電壓負反饋控制環節，以此減小負載電壓波動。