基本不等式教學中的幾個問題情境

寧紅國

（河北欒城中學，河北 石家莊 051430）

《普通高中數學課程標準（2017 年版）》要求要了解并會證明基本不等式；會用基本不等式解決最值問題。對于基本不等式的考查幾乎每年高考都會涉及，難點在于變形化簡構造成基本不等式的基本結構，還要注意“一正二定三相等”。對于基本不等式的證明，可以培養學生數形結合的數學思想。在應用的過程中，通過條件的轉換和變式，培養學生形成類比歸納的思想和習慣，進而形成嚴謹的思維方式。

情境問題一：把一個物體放在天平的一個盤子上，在另一個盤子上放一砝碼使天平平衡，稱得物體的質量為a，由于天平不準確，天平的二臂長略有不同（其他因素不計），那么a 并非實際質量，不過，我們可作第二次測量，把物體調換到天平的另一個盤子上，此時稱得物體的質量為b.那么物體的實際質量是多少呢？

情境問題二：某商場對商品價格進行了調整，有下面幾種打折方式，問哪一種打折方式對顧客更有利：①先打8 折，再打4 折；②先打7折，再打5 折；③先打6 折，再打6 折；④先打a折，再打b 折；⑤先打折，再打折.引導學生分別計算打折數量：①0.8×0.4=0.32 ②0.7×0.5=0.35 ③0.6×0.6=0.36 ④打ab 折 ⑤打折，從中可以看出兩次打折的數據差值越大，商品價格越低，顧客越有利.所以可猜想ab≤（）2，由于a≥0，b≥0，上式兩邊開方得（a≥0，b≥0），又體現基本不等式的應用.

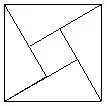
情境問題三：在一個正方形中，畫出四個全等的直角三角形（如右圖），其直角邊分別為a、b，則四個三角形的面積和為2ab，正方形的邊長為，由圖形可得：四個三角形的面積和小于正方形的面積即2ab≤a2+b2，因為a≥0，b≥0，用去替換a、b，得出（a≥0，b≥0）.這種方法中體現換元法的應用.

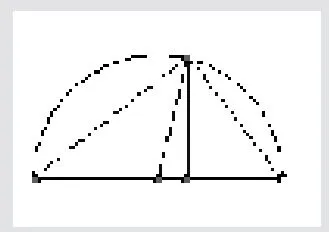
情境問題四：如右圖，在一個半圓中，圓心為O，AC 為直徑，B 是圓弧上一點，則∠ABC=90°，設AD=a、CD=b、BD=h 已知BD⊥AC，那么OB=，由垂線定理知h2=ab，由圖形可知BD≤OB 即，從而得到基本不等式.

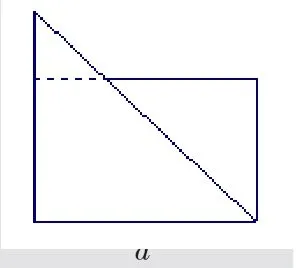
情境問題五：畫出兩個等腰三角形（如右圖），直角邊分別為a、b，且三角形的兩腰重合，由圖可知：兩三角形的面積和大于以a、b 為邊長的矩形的面積，即≥ab，然后同問題三的處理，可以看出當a、b 長度逐漸接近時，兩圖形面積逐漸接近，所以當a=b時取“=”，基本不等式成立.

基本不等式知識點作為高考中的重要考點,可以單獨以填空選擇形式考查,也可以與其他熱門考點（三角，解析幾何）結合以綜合題形式進行考查,是求最值問題最有利的工具。因而，教學中要求學生正確應用基本不等式進行判斷和計算，熟練掌握基本不等式的變形應用。我們在學習和教學的過程還是要重視基礎，回歸教材，突出雙基。