基于PSO的模型預測速度控制權重系數自整定

梅容魁，于新紅

(1.福州大學 電氣工程與自動化學院，福州 350108；2.電機驅動與功率電子國家地方聯合工程研究中心，中國科學院海西研究院泉州裝備制造研究中心，泉州 362200)

0 引 言

隨著電力電子技術與現代電機控制理論的快速發展，永磁同步電機(以下簡稱PMSM)已經成為當下工業生產熱門的話題[1-3]。模型預測控制(以下簡稱MPC)作為一種現代控制算法，以其原理簡單、動態快速等優點，引起了廣泛的研究和關注[4]。MPC的控制思想是通過建立系統的數學模型來預測不同時刻下系統的狀態值，然后通過最小化預定義的成本函數來選擇最佳電壓矢量[5]。從控制目標的角度來看，大多數MPC策略側重于電流、轉矩/通量或速度控制[6-8]。其中模型預測速度控制(以下簡稱MPSC)將速度作為主要控制目標，克服傳統級聯控制結構，提升系統的動態性能[9-10]。由于成本函數中引入了速度量，故成本函數中的權重系數難以確定。

粒子群優化(以下簡稱PSO)算法是Russell Eberhart和James Kennedy在1995年提出的一種基于種群的智能算法，通過種群協作尋找粒子的最優位置[11-12]。PSO算法由于不受系統模型、參數變化等因素影響，在參數辨識和參數優化等方面中得到了廣泛的應用[13]。文獻[14]提出了一種基于PSO算法的估計器，可有效地估計出轉子磁鏈和定子電阻，但所采用的PSO算法在處理時變多參數問題時往往容易陷入到局部的最小值，導致無法同時識別系統所有參數。文獻[15]利用PSO算法對控制系統的參數進行了優化處理，達到了參數自整定的目的。

本文提出一種基于改進PSO的模型預測速度控制權重系數在線自整定方法，將電流誤差的均方根值作為PSO的目標函數，通過迭代尋優獲得符合最小化目標函數的權重系數。改進的PSO算法加強局部和全局的探索性能，促進了粒子收斂到最優解，并在實驗平臺上驗證了該算法的有效性。

1 PMSM數學模型與模型預測速度控制

本文采用表貼式永磁同步電機，在d-q參考系下電流方程可以表示如下：

(1)

式中：id和iq為d-q坐標系下的電流分量；ud和uq為d-q坐標系下的電壓分量；Rs為定子電阻；Ls為定子電感；ωe為電角速度；ψf為永磁體磁鏈。

PMSM的機械和電磁轉矩方程如下：

(2)

Te=1.5pψfiq

(3)

式中：p為極對數；Tl為負載轉矩；ωm為機械角速度；Bm為摩擦系數；J為轉動慣量。

將式(1)離散化得：

(4)

式中：id(k)和iq(k)為當前時刻電流采樣值；id(k+1)和iq(k+1)為下一時刻電流的預測值；ud(k)和uq(k)為所施加的電壓；Ts為采樣周期。離散化式(2)和式(3)可得：

(5)

Te(k+1)=1.5pψfiq(k+1)

(6)

為了減小預測的誤差，采用平均電磁轉矩：

(7)

預測速度方程改寫：

(8)

將7個電壓矢量代入式(4)、式(6)、式(7)和式(8)，可以得到id(k+1)，iq(k+1)和ωm(k+1)，并選擇使成本函數最小的電壓矢量，將其對應的開關狀態應用到逆變器。成本函數表示為：

(9)

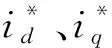
在穩態下，電磁轉矩Te和負載轉矩Tl可認為是相等的，Tl可由負載觀測器得到。根據式(6)，q軸電流參考值可表示如下：

(10)

圖1為模型預測速度控制框圖，通過負載轉矩觀測器得到轉矩量，然后利用電流和轉速預測模型得到下一時刻的電流和轉速量，最后選取使成本函數最小的電壓矢量。

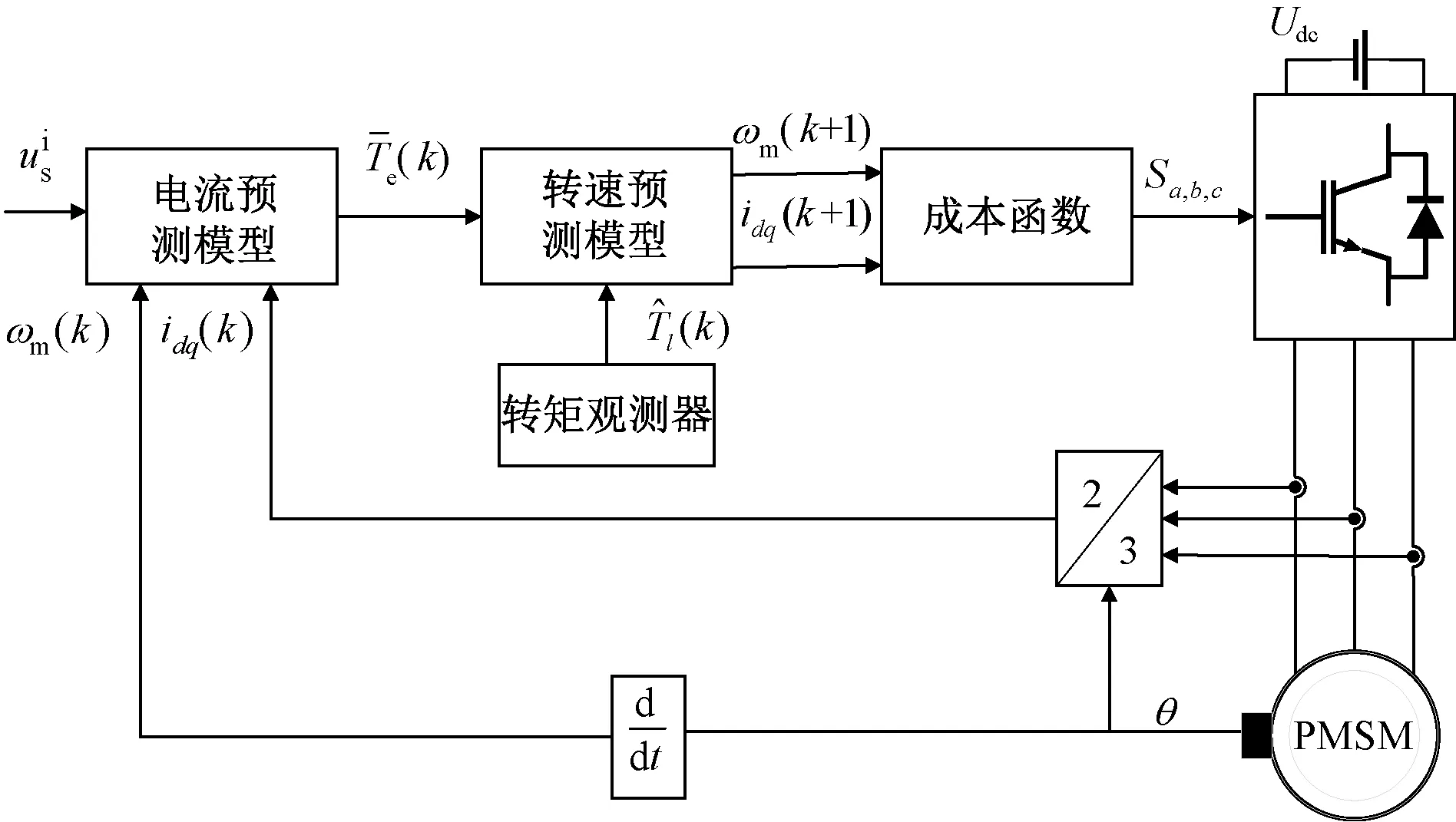
圖1 模型預測速度控制框圖

2 滑模轉矩觀測器設計

本文采用滑模觀測器的方式獲取負載轉矩量，可有效降低外部負載擾動的影響，同時可省去額外的設備要求。

(11)

式中：K為切換參數。根據電機機械方程式(2)，負載轉矩作為擴展變量，則擴展滑模負載轉矩觀測器可構造如下：

(12)

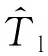
為了保證滑模的穩定性，應選擇合理的觀測器參數。首先，速度和轉矩的誤差方程定義如下：

(13)

由于系統的控制頻率較高，負載轉矩Tl可以認為是一個常數，根據式(12)，誤差的微分方程可以表示：

(14)

為了保證滑模觀測器的穩定性，必須滿足以下等式：

(15)

可得到K的取值范圍如下：

(16)

因此，具有參數K的滑模觀測器可以在有限時間內到達滑模表面并停留其上。則滑模面S及其微分形式都等于零，即：

(17)

然后，將式(17) 代入式 (14) 得到：

(18)

此外，式(18)可以簡化為：

(19)

為保證轉矩估計誤差收斂為零，滑模觀測器中的參數g應滿足g< 0。

3 基于改進PSO算法的權重系數自整定

3.1 傳統粒子群

將PSO算法中的每一個粒子位置代表一個權重系數，粒子每一次更新位置后，根據目標函數來判斷目前是否為最優位置。其中，目標函數采用電流誤差的均方根值，設計如下：

f=rms(Δid)+rms(Δiq)

(20)

PSO算法在每一次迭代中記錄個體最優位置和全局最優位置，并用于更新種群中粒子的位置和速度信息，其中更新的方法如下：

(21)

為了提高PSO算法的搜索性能，本文采用動態線性的慣性權重系數，權重系數ω可以設置為從ωmax=0.8到ωmin=0.1。c1和c2采用異步時變設置方式。該方法的目的是在搜索前期加強局部的搜索能力，在搜索后期促使所有粒子收斂的全局最優位置。具體方法如下：

(22)

(23)

式中:N為迭代次數；Nc為最大迭代次數；c1 max=c2 max=2；c1 min=c2 min=0.2。圖2為PSO算法的流程圖，采用式(13)更新粒子的速度和位置，權重系數ω采用動態線性的方式，學習因子采用異步時變方式，來提升局部和全局探索性能。

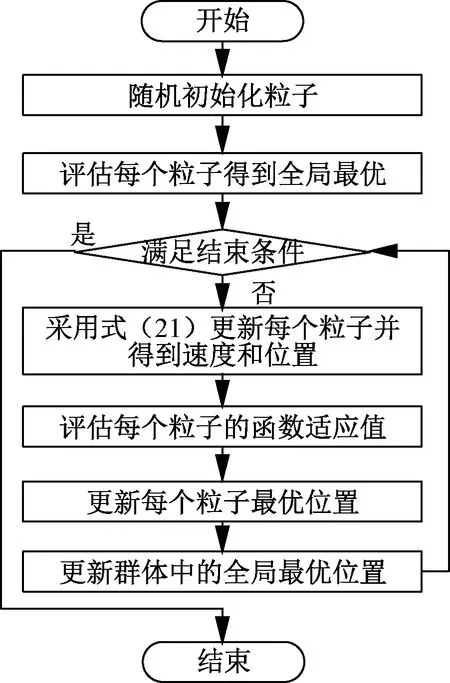
圖2 PSO算法流程圖

3.2 混沌變異粒子群

混沌的特性普遍存在于自然界，并具有隨機、遍歷等特點，在PSO算法中加入混沌變異的特性可提升PSO算法的局部搜索能力。本文采用如下的混沌方程：

(24)

式中：τ為混沌變量。當u介于3.56和4之間時，可使粒子進入混沌的狀態，本文中u設置為3.8。

基于混沌變異的PSO算法的具體步驟如下：

(1)將粒子群中的粒子全部映射到混沌方程的定義域(0,1)中，即：

(25)

式中：pxk(r)、pxk(max)、pxk(min)分別為粒子群種群中的任一粒子、最大的粒子和最小的粒子。

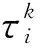
(26)

(3)將混沌序列映射到原粒子群空間:

(27)

式中：i=1,2,…n，n為該粒子群中粒子個數，通過映射變為一組混沌變異的粒子種群，最后將該粒子種群替換原粒子種群進行迭代尋優。

4 仿真與實驗分析

4.1 仿真分析

為了驗證改進的粒子群算法對模型預測速度中權重系數在線自整定的可行性，利用MATLAB仿真環境分別設計了模型預測速度控制和改進后混沌PSO算法。算法中的控制周期采用Ts=50 μs，仿真和實驗的電機參數如表1所示。

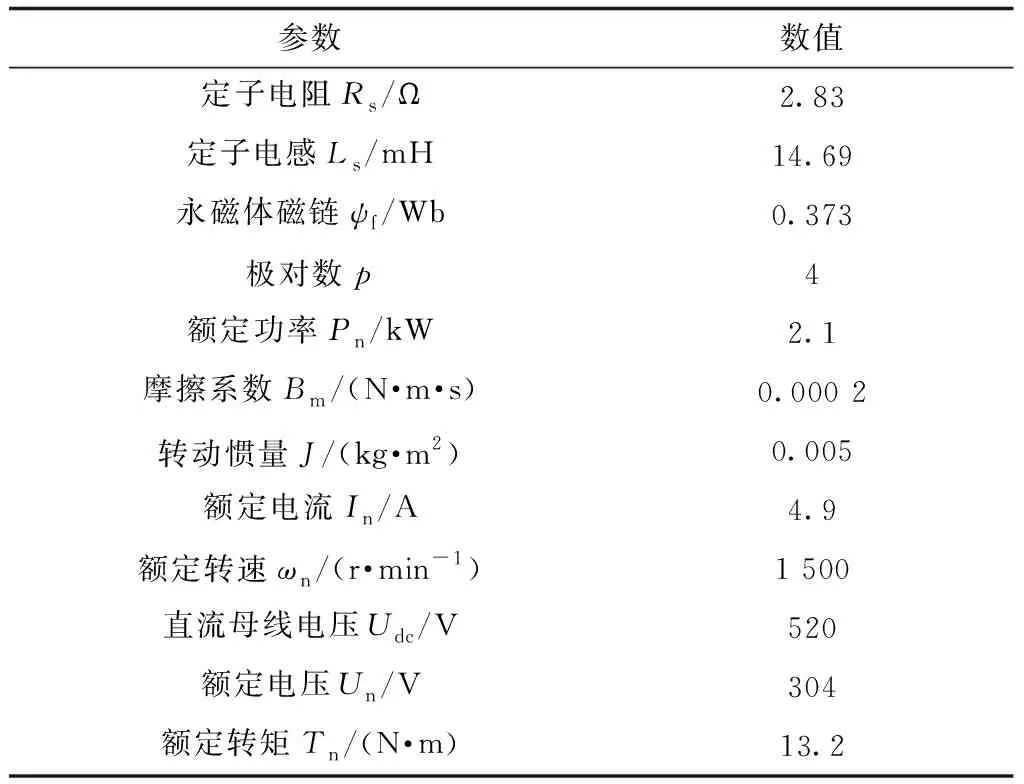
表1 永磁同步電機參數

設置PSO算法中總的粒子個數為12，最大迭代次數為120，每個粒子維度為3，粒子三個維度的位置范圍分別設置為[5,100]，[1,2]和[1,2]，對應λω、λd和λq三個權重系數的整定范圍，對應的粒子速度范圍分別[-50,50]，[-0.5,0.5]和[-0.5,0.5]。為了減少PSO算法在權重系數整定過程中的運行時間，當全局最優的位置保持20代不變時，則停止迭代，輸出全局最優值。

圖3為轉速600 r/min, 加載10 N·m時，粒子群適應度值對比圖，可以看出，改進后的混沌PSO算法相比傳統的PSO，具有更快的收斂性能和探索精度。

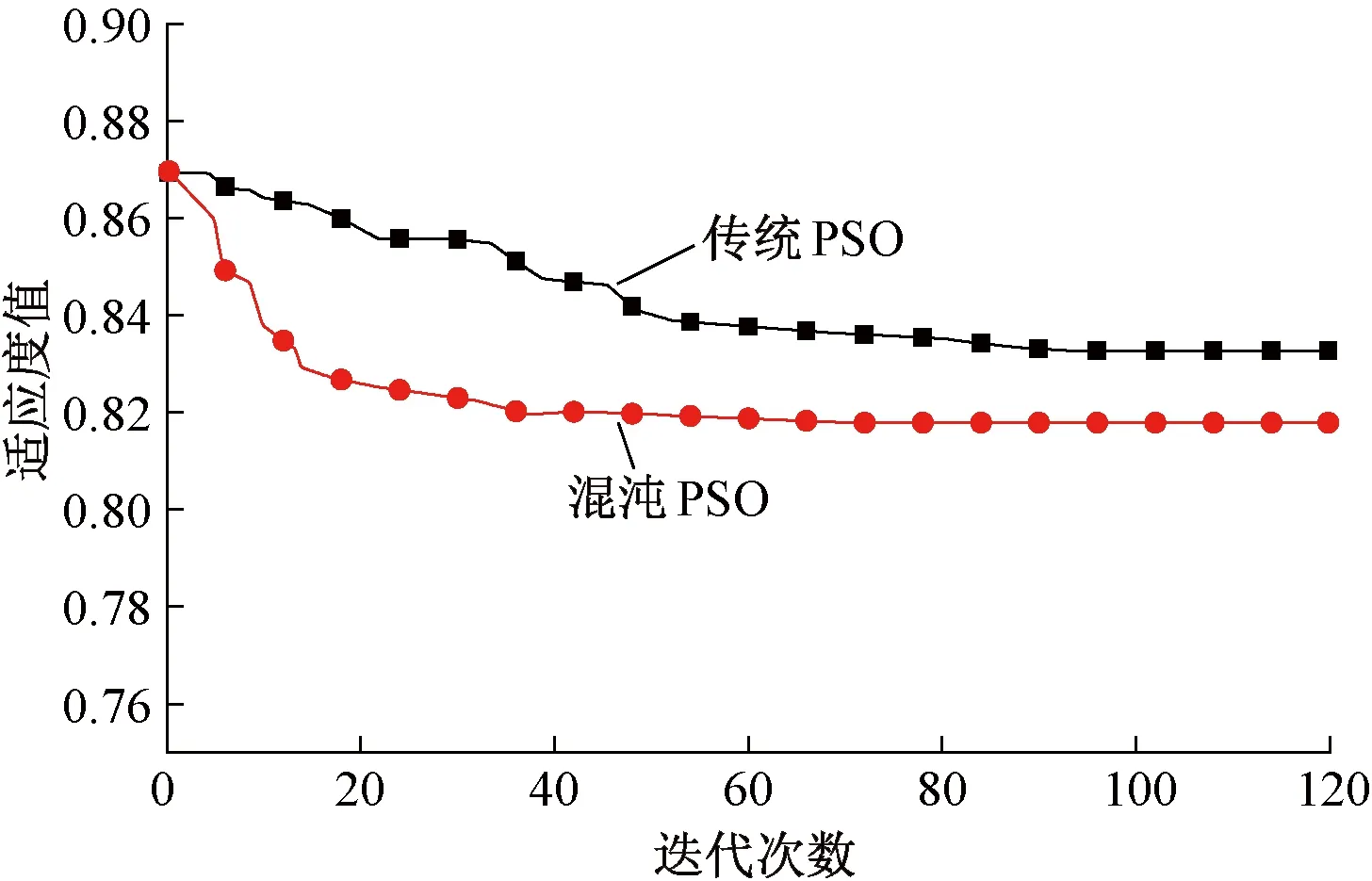
圖3 轉速600 r/min, 加載10 N·m時，粒子群適應度值對比

圖4為混沌PSO權重系數整定過程，可以看出權重系數λω、λd和λq分別收斂到67.2，1.03和2.02。圖5為轉速600 r/min, 負載加載10 N·m時的混沌PSO算法整定前后轉速波形對比，系統起動時采用固定權重系數(λω=5,λd=1,λq=1)，轉速存在3 r/min的穩態誤差，當加入改進后的PSO算法進行整定后可以有效地消除穩態誤差。因此，利用改進PSO算法自整定的權重系數具有更好的穩態性能。

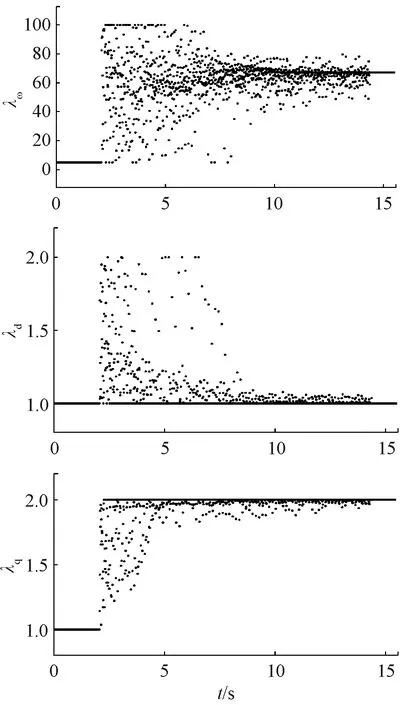
圖4 轉速600 r/min, 加載10 N·m時，權重系數整定過程

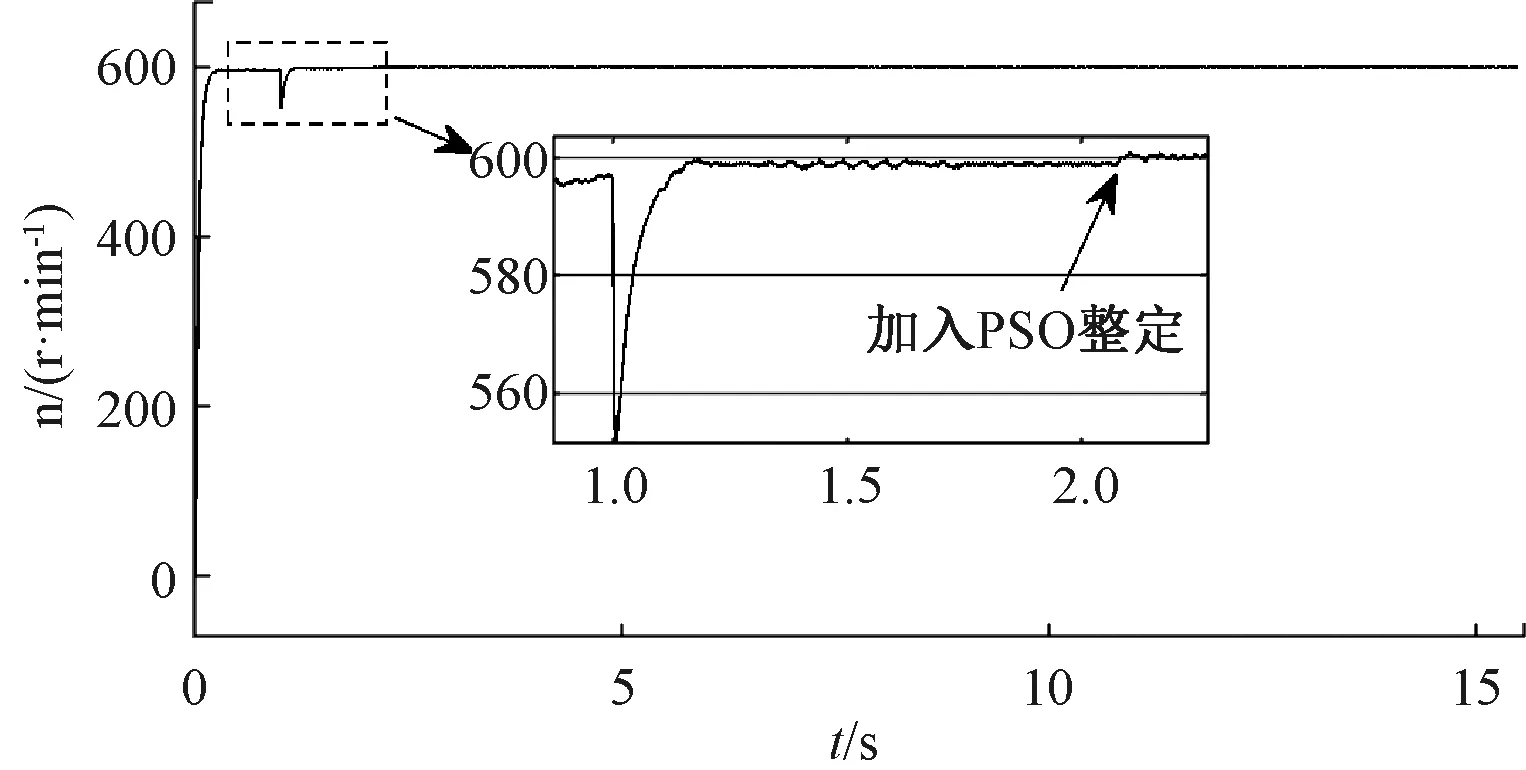
圖5 PSO算法整定前后轉速波形對比

4.2 實驗分析

如圖6所示為實驗平臺，其中包括二臺2.1 kW表面式PMSM，分別配備2 500脈沖/轉(P/R) 增量式編碼器，逆變器直接從一個520 V直流電源供電。其中，算法部分在dSPACE平臺上運行，dSPACE的控制板包括DS4003數字I/O板、DS2004高速A/D板、DS3002增量式編碼器接口板和DS1007 PPC處理器板。系統的控制頻率和采樣頻率使用的是20 kHz，負載電機由一個4 kW MICNO KE600 A逆變器驅動。采用3個AVD±15A霍爾電流傳感器對定子電流進行實時采樣，采樣精度為2%。

圖6 實驗平臺

為了對比穩態下電流紋波，選取一組固定的權重系數(λω=5,λd=1,λq=1)進行對比，圖7為轉速600 r/min, 負載加載10 N·m時，固定權重系數的穩態電流波形。圖8為相同工況下，采用改進的混沌PSO算法在線自整定后的的穩態電流波形，可以看出，采用自整定權重系數后的電流THD從9.55%降低為7.9%，有效地提高了電流質量。

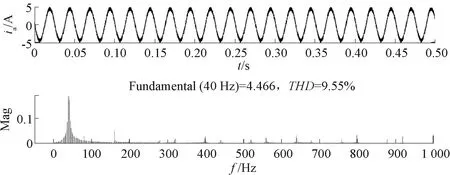
圖7 固定權重系數下的穩態電流波形

5 結 語

本文針對模型預測速度控制，利用改進的PSO算法對成本函數中的三個權重系數進行在線的自整定，并在傳統的模型預測速度控制中加入滑模觀測器，減小外部擾動的影響。其中，將實際電流與參考電流誤差的均方根作為PSO算法的目標函數，通過迭代尋優獲得符合最小化目標函數的權重系數。改進后的混沌PSO提升了傳統PSO算法局部和全局的搜索性能。實驗結果表明了改進的PSO算法整定的權重系數滿足系統要求，并具有良好的穩態性能。