基于線性擴張狀態觀測器的PMSM無位置傳感器控制

曾香平，趙世偉，尹華杰，肖盼盼

(華南理工大學 電力學院，廣州 510640)

0 引 言

永磁同步電機(以下簡稱PMSM)依靠永磁體勵磁，與傳統電勵磁電機相比，其結構簡單、轉矩密度大、效率高，廣泛應用于要求功率密度高、調速范圍廣的場景。PMSM調速系統需要反饋速度與位置信號[1]，采用物理傳感器如位置霍爾傳感器或編碼器將增加電機的體積和成本，降低系統的運行可靠性[2]。

有學者提出從定子側易測物理量(電壓、電流)中提取與轉速、位置相關的量，從而實現無位置傳感器控制[3]。根據適用速度范圍不同，PMSM無位置傳感器控制策略可分為兩類：零低速時，利用電機凸極特性設計無位置傳感器控制，例如高頻注入法[4]；中高速時，利用觀測器觀測反電動勢或者磁鏈，再結合正切計算法或鎖相環(以下簡稱PLL)估計電機轉速和轉子位置，實現無位置傳感器控制[5-6]。

無位置傳感器控制中常用的觀測器有滑模觀測器[7]、模型參考自適應觀測器[8]、擴展卡爾曼濾波器觀測器[9]等。傳統滑模觀測器適應性強，對參數變化魯棒性較好，但其變結構控制方式引入了抖振。模型參考自適應觀測器觀測精度高，但對電機模型依賴強，抗擾動能力差。擴展卡爾曼濾波器有較強的抗擾性，但需要通過大量復雜的矩陣運算才能實現觀測，對硬件的計算能力要求高。

擴張狀態觀測器(以下簡稱ESO)是自抗擾控制器中核心環節。文獻[10]提出構造兩個非線性ESO，利用電機電壓方程和機械方程，分別觀測電機反電動勢和轉速。基于ESO的無位置傳感器控制觀測精度高、抗擾動能力強，相比于非線性觀測器，線性擴張狀態觀測器(以下簡稱LESO)調參更方便，且可以實現頻域分析[11-12]。

本文提出利用LESO觀測反電動勢。LESO為線性模型，易于進行理論分析，可以通過頻域法推導觀測反電動勢與實際反電動勢之間的傳遞函數，獲得觀測反電動勢相位滯后角的數學計算公式。為了提取反電動勢觀中的速度、位置信息，本文利用三角函數構造位置差頻信號，通過PLL準確提取反電動勢信號中的轉速、位置信號。相比于傳統正切計算法，PLL能夠抑制觀測反電動勢誤差帶來的噪聲。最后通過MATLAB仿真和實驗驗證該方案能夠準確獲得電機轉速和轉子位置信號，實現無位置傳感器轉速控制。

1 表貼式PMSM的數學模型

表貼式PMSM氣隙磁場均勻，交軸電感和直軸電感差異很小，電機可視為隱極。假設電機三相定子繞組對稱，電機旋轉時定子側感應反電動勢波形為標準正弦波，忽略鐵心飽和，則表貼式PMSM在靜止α，β軸坐標系中的定子電壓方程：

(1)

式中：uα，uβ，iα，iβ，eα，eβ分別為α，β坐標系下電壓、電流以及反電動勢；R為定子相電阻；L為定子相電感。

電機旋轉，永磁體感應出的反電動勢：

(2)

式中：ψf為永磁體磁鏈；ω為電機電角速度；θ為轉子N極與a相軸線的夾角。

2 基于LESO的反電動勢觀測

2.1 LESO設計

由式(1)可見，α，β坐標系下兩個電壓方程相互解耦，且兩個電壓方程除下標外完全一致，以下僅以α軸電壓方程為例進行陳述。將反電動勢視為未知量，引入“擴張狀態”：

(3)

反電動勢可微分求導數，設：

(4)

可以將式(1)中α軸電壓方程寫成狀態空間方程：

(5)

定義觀測誤差：

(6)

(7)

可構造LESO：

(8)

式中：β1α、β2α為觀測器參數。

2.2 LESO收斂性證明

將式(8)的觀測器與原系統擴張狀態式(5)作差，得到：

(9)

改寫成矩陣形式如下：

(10)

觀測器參數可配置如下：

(11)

式中：ω0>0。對式(10)進行拉氏變換：

(12)

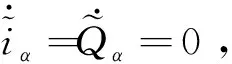
(13)

因此，可以增大ω0，使得LESO觀測精度滿足要求，實現系統狀態觀測。

2.3 ESO觀測反電動勢分析

(14)

即:

(15)

根據式(15)，繪制Bode圖如圖1所示。

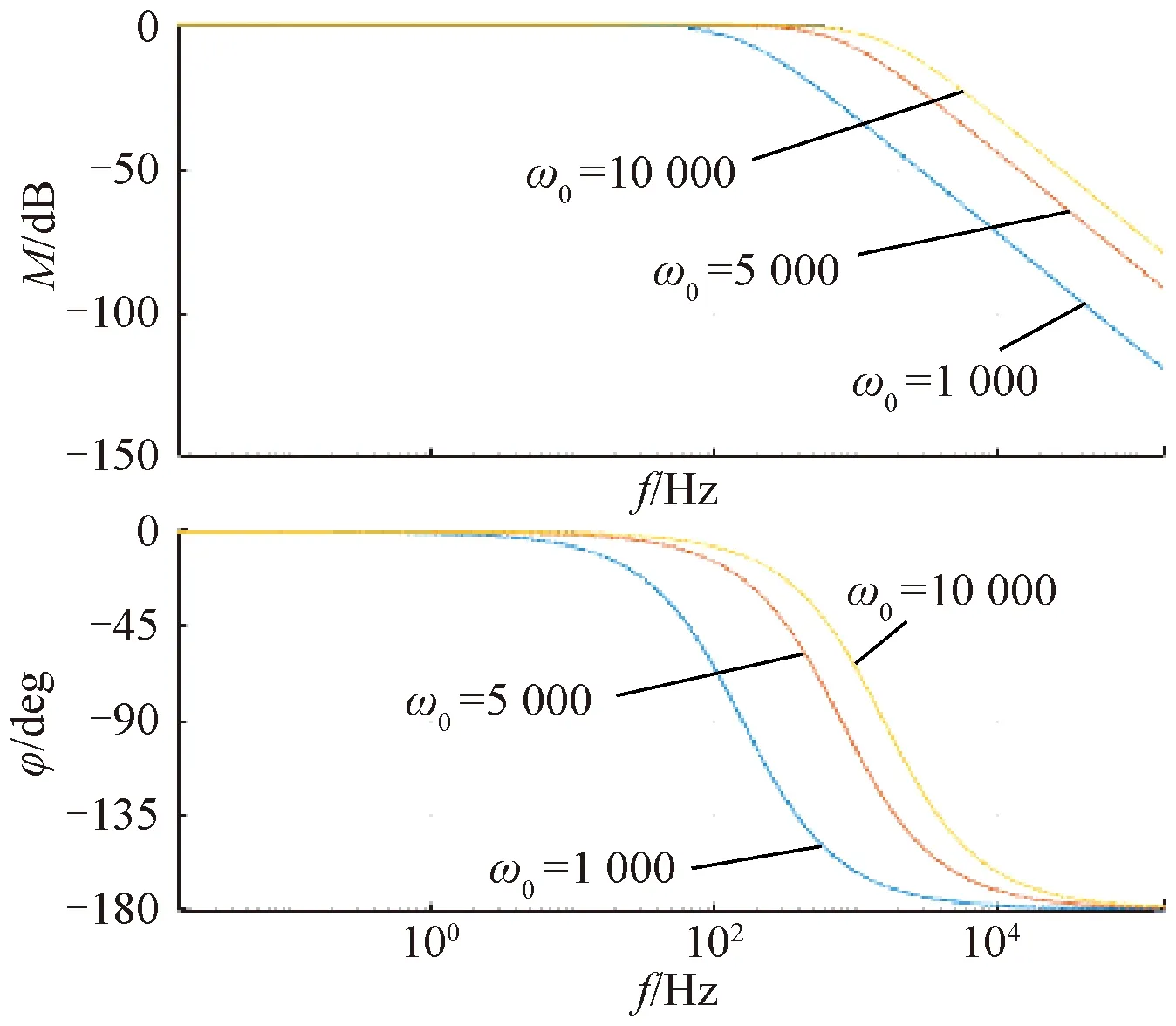
圖1 反電動勢觀測值與實際值傳遞函數Bode圖

從幅頻特性可以看出，觀測器具有低通特性，而且隨著ω0的提高，幅頻特性會往右移動，從而導致帶寬增加，其高頻增益也相應提高。因此ω0可以表征觀測器的帶寬。從相頻特性可以看出，隨著頻率提高相位滯后角度會隨之加大，但是隨著ω0的提高，相同頻率下的相位滯后會相應減小。

對于該觀測器來說，帶寬過小，相位滯后會比較明顯；帶寬過大，容易引入高頻干擾，所以需要依據系統實際需求選擇恰當的帶寬。

3 基于PLL的位置觀測

3.1 PLL設計

設計PLL提取反電動勢觀測值中的速度位置信號。PLL的結構如圖2所示。

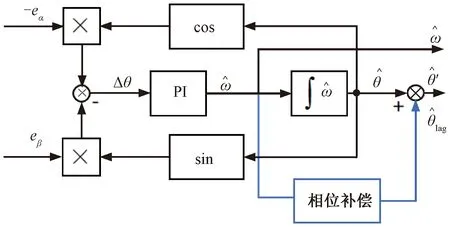
圖2 PLL結構圖

由式(2)和圖2可以得到：

(16)

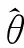
(17)

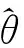
(18)

式中：kp和ki為PI環節系數。合理配置kp和ki，可以利用式(18)的低通特性獲得平滑且準確的位置估算信息。

3.2 相位補償

根據頻域法，式(15)可寫作：

(19)

可見，傳遞函數式(19)的相頻特性：

(20)

即觀測反電動勢相位滯后：

(21)

最終觀測位置：

(22)

4 仿真與實驗

4.1 仿真分析

為了驗證該策略的可行性，利用MATLAB搭建如圖3所示的仿真模型，電機參數設置如表1所示。

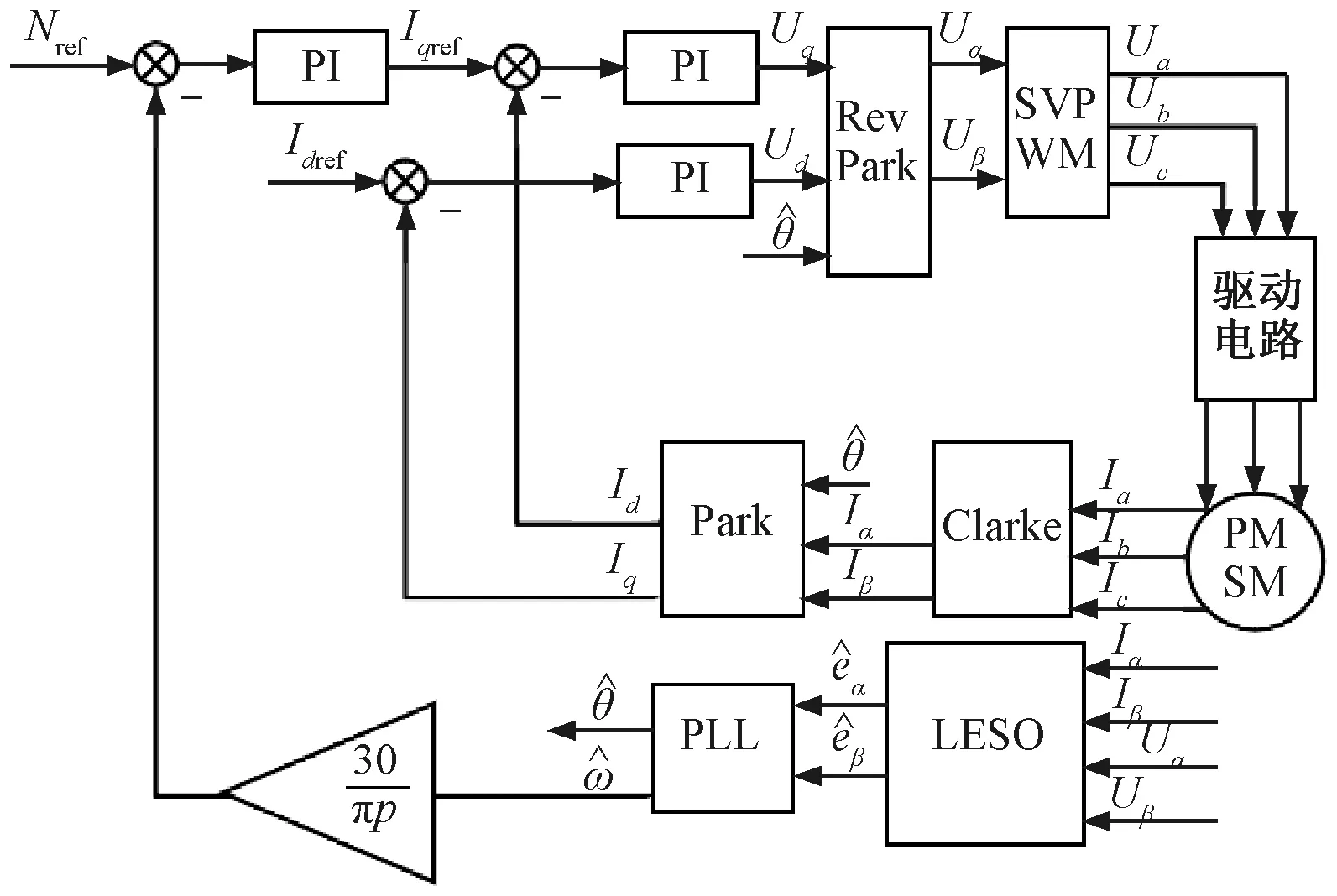
圖3 仿真實驗原理框圖

表1 仿真電機參數模型

在仿真過程中，最初的參考轉速設置為750 r/min，在1 s時參考轉速改為1 500 r/min。結合仿真需求，電機運行的最高轉速不超過1 500 r/min，即反電動勢的頻率不高于100 Hz，設置LESO參數ω0=5 000。由圖1可見，此時LESO的截止頻率511 Hz。100 Hz的反電動勢信號通過LESO幅值損失幾乎為0，相位滯后約為14°，需要做相位補償。并設置PLL中的參數Kkp=5 000；Kki=800。

首先驗證LESO能夠精確觀測反電動勢。系統速度和位置反饋均由電機輸出實際值提供。觀測器只做觀測，其輸出觀測值不參與閉環。圖4為LESO觀測的反電動勢穩態值。

圖4 觀測反電動勢結果比較

由圖4波形可以看出，LESO觀測的反電動勢正弦度高，諧波含量小。對觀測反電勢穩態值進行傅里葉分解，轉速為750 r/min時，諧波畸變率為1.4%；轉速為1 500 r/min時，諧波畸變率為0.7%。這是因為低速時，電機反電動勢幅值較小、信噪比較低。

觀測反電動勢經過PLL獲得的位置信號如圖5所示，位置觀測誤差如圖6所示。

圖5 位置觀測結果比較

圖6 觀測位置誤差比較

當位置設有相位補償時，電機轉速為750 r/min，觀測位置誤差為6°；轉速為1 500 r/min，觀測位置誤差為15°。位置角度補償后，兩種轉速下的相位滯后皆為0.5°。可見，利用式(19)可以有效補償相位滯后，提高控制策略適用速度范圍。

速度觀測值如圖7所示。

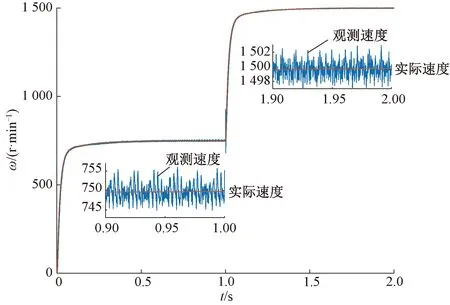
圖7 觀測器開環速度觀測結果比較

可見，穩態時轉速估計精度高。在750 r/min時，速度觀測值波動范圍約為(750±2) r/min；轉速為1 500 r/min時，速度觀測值的波動范圍約為(1 500±5) r/min，相比于低速，高速時速度觀測值更平滑。

將觀測器投入系統，閉環系統的速度響應如圖8所示。

圖8 觀測器閉環速度觀測結果比較

觀測速度存在一定程度的波動，但經過系統慣性環節，實際速度響應曲線平滑。利用該控制策略可以實現無位置傳感器速度控制。

4.2 實驗分析

實驗平臺如圖9所示，實驗電機與仿真模型中的電機參數一致，控制器驅動板主控芯片為STM32F103RCT6，驅動電路三相全橋逆變器開關頻率為10 kHz，通過串口總線與PC上位機相聯接，傳輸觀測器觀測的位置信號和速度信號，以及編碼器輸出的位置信號和速度信號。

圖9 實驗平臺

設置參考轉速750 r/min，在3 s時，參考轉速突變為1 500 r/min。當觀測器觀測速度平均值與編碼器觀測速度平均值誤差小于6 r/min時，從有傳感器控制系統切換為無位置傳感控制系統。LESO+PLL觀測的位置信號和編碼器觀測的位置信號對比如圖10所示，LESO+PLL觀測的轉速曲線和編碼器觀測的轉速對比如圖11所示。

圖10 實際位置與觀測位置比較

圖11 實際速度與觀測速度比較

從圖10可以看出，不同轉速下的觀測位置與實際轉子位置重合，觀測效果較好。由圖11可以看出，速度觀測平均值都能收斂到實際轉速。

5 結 語

本文利用LESO觀測表貼式PMSM反電動勢，證明了觀測器的收斂性，且利用觀測反電動勢與實際反電動勢之間的傳遞函數，討論了LESO相關參數的設置方法，推導了補償角的計算公式。在此基礎上，本文采用PLL估計了電機轉速和轉子位置。

本文搭建了無傳感器的仿真模型與實驗平臺，對位置估計和無傳感器速度控制進行了仿真和實驗對比分析。仿真和實驗結果均能實現準確的轉子位置估計，與理論分析較為吻合，驗證了本文所提出的LESO+PLL位置估計算法和無傳感器速度控制方案的有效性。