鉆柱粘滑振動仿真和控制策略研究

陳午陽,劉曙光,胡小雄

(1. 黃山學院 機電工程學院，安徽 黃山 245800;2.中國科學院 寧波材料技術與工程研究所，浙江 寧波315211;3.星宇電子(寧波)有限公司，浙江 寧波 315514)

在深井石油鉆探過程中，常發生極具破環性的鉆柱粘滑振動，嚴重時會造成鉆桿鉆速降低、組合鉆具失效，甚至鉆桿斷裂[1]。如何消除鉆井中的粘滑振動成為亟需解決的工程難題。導致這些振動的主要原因包括：鉆桿與井壁間摩擦、鉆頭與巖層剪切面之間的接觸摩擦、井眼偏斜、鉆桿旋轉不平衡、及各種線性或非線性的共振[2-3]。

隨著井深的增加，巖石的塑性和硬度增大，鉆桿的扭轉剛度相對降低[4]。由于鉆頭很難克服巖石、砂礫產生的靜摩擦轉矩，在短時間內鉆頭會產生停鉆、卡鉆現象，此時為鉆頭的粘滯階段[5]。頂驅或轉盤一直帶動鉆柱及井下鉆具轉動，當積蓄在鉆柱中的扭轉勢能足以破壞巖層時，鉆頭上積累的驅動力矩就會非常大。當驅動力矩超過井下巖石與鉆頭產生的摩擦力矩時，鉆頭會突破粘滯，進入滑脫狀態，并在正反方向上加速或減速，有時鉆頭的角速度會達到頂驅電機轉速的數倍[6-7]。如此大的扭轉沖擊，如果超過設備所能承受的極限轉矩，危險情況下會迫使鉆井設備停止運行。

本文依據二自由度彈簧-扭擺鉆柱動力學模型，推導出鉆頭運轉狀態方程，設計一種轉速負反饋閉環調節和轉矩負反饋閉環調節的雙閉環控制方法[8-9]。此方法能及時調整頂驅電機轉速，改善井底鉆具組合運轉狀態，達到抑制滑鉆或卡鉆的目的。

1 鉆柱粘滑振動力學模型

1.1 數學模型的建立及分析

鉆柱結構分外圈和套管，而鉆柱處在內外有鉆井液的封閉環境中。由于單個鉆桿的直徑很小，會使鉆出的井眼很小。鉆桿在地面裝置的驅動下，會受到井底地層各種巖石的作用力。除此之外，還會受到鉆頭與巖層砂礫相互作用的干擾力，以及鉆柱本身的慣性力。綜合分析鉆柱系統具有的復雜性，不利于建立模型。為此做以下簡化：

1) 不考慮橫向振動和縱向振動與扭轉振動產生的耦合效應，單單考慮扭轉振動[10-11]。

2) 對鉆柱系統進行抽象性處理，將其等效成頂驅電機和轉盤。

鉆具組合和鉆頭的二自由度數學模型如圖1所示。

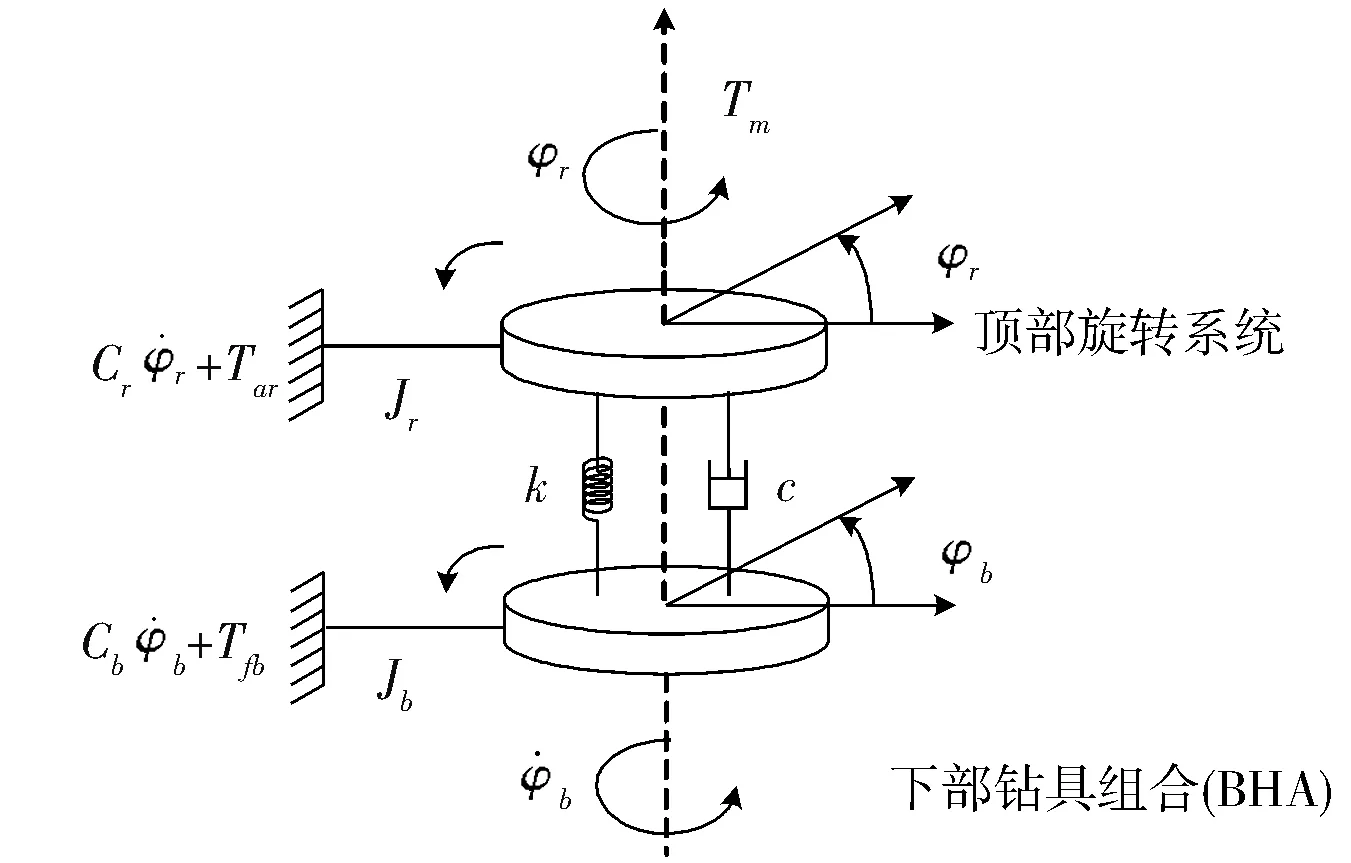
圖1 鉆柱二自由度扭轉擺模型

按照圖1中的等效模型，根據旋轉剛體力學原理，可得頂驅轉盤的運動方程：

(1)

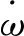
Tt和Tar的表達式：

(2)

Tar=crωr

(3)

式中：cr為頂驅阻尼系數；c為等效粘滯系數；k為等效剛度系數；φr為頂驅旋轉角度；φb為下部鉆組合旋轉角度；ωr為頂驅轉盤的角速度。

建立鉆柱系統的運動學方程：

(4)

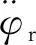
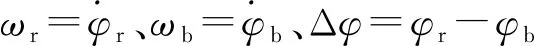
(5)

用狀態空間方程改寫式(5)得：

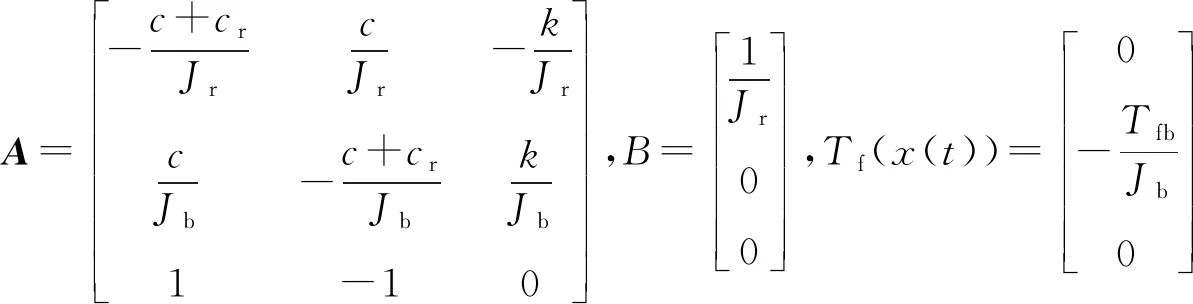
(6)

在頂驅轉速保持不變的情況下，式(6)可變換為式(7)：

(7)

通過以上數學公式對鉆柱扭轉行為的描述，發現粘滑振動現象的產生與等效阻尼系數和等效扭轉剛度系數有關，其根本的關系是鉆桿的長度。當鉆桿長度增加時，扭轉剛度系數降低，粘滯阻尼系數加大。若此時不增加電機轉速或者降低鉆壓，底部鉆頭將會發生粘滑現象。為進一步獲取粘滑振動的行為狀態，可借助Simulink模擬器觀測鉆頭的轉矩和轉速的變化情形。

1.2 二自由度的建模仿真分析

為使建立的鉆柱數學模型中，頂驅給定的轉速值與轉矩值和鉆頭的轉速與轉矩的關系曲線凸顯出來，使用了MATLAB工具。在Simulink編輯器中建立二自由度的鉆柱數學模型，仿真粘滑的產生過程。借助Simulink中的示波器元件實時顯示鉆頭的動態響應曲線，并借助該曲線給定頂驅電機不同的轉速值，對不同狀態下的鉆頭速度和轉矩進行實時分析。以下將通過轉速控制模式進行系統地分析。

依據式(7)中得出的鉆頭角速度ωb和頂驅驅動轉矩Tm的計算公式，分別給定輸入頂驅轉速值ωr=4 rad/s和ωr=8 rad/s，分析對比鉆頭的轉速和轉矩的狀態曲線。圖2所示為轉速模式控制下，二自由度的Simulink建模仿真框圖。

1-輸入電機轉速ωr；2-ωb與ωr角速度差；3-等效粘滯系數c；4-積分器角度差；5-等效剛度系數k；6-頂驅阻尼系數cr；7-頂驅轉盤和鉆具組合之間的耦合力矩Tt；8-頂驅輸出轉矩Tm；9-靜態平衡力矩Teb；10-Teb與Tfb扭矩差；11-鉆頭阻尼系數cb；12-鉆頭角加速度；13-積分器鉆頭角速度；14-鉆頭扭矩。圖2 速控模式下仿真框圖

通過改變ωr值，對鉆頭角速度ωb和鉆頭轉矩Tfb進行分析。當ωr=4 rad/s時，Simulink仿真結果如圖3所示，鉆頭出現周期性地粘滯與滑脫現象，其最高轉速可達頂驅轉速的2倍以上，這與理論研究的數據貼合。在圖3b中，鉆頭的轉矩波動出現大幅度的震蕩，有時會出現負值，顯然鉆頭的轉速和頂驅的力矩會隨著鉆頭的非線性摩擦力矩的波動而上下大幅震蕩，此時鉆柱系統已出現粘滑振動。

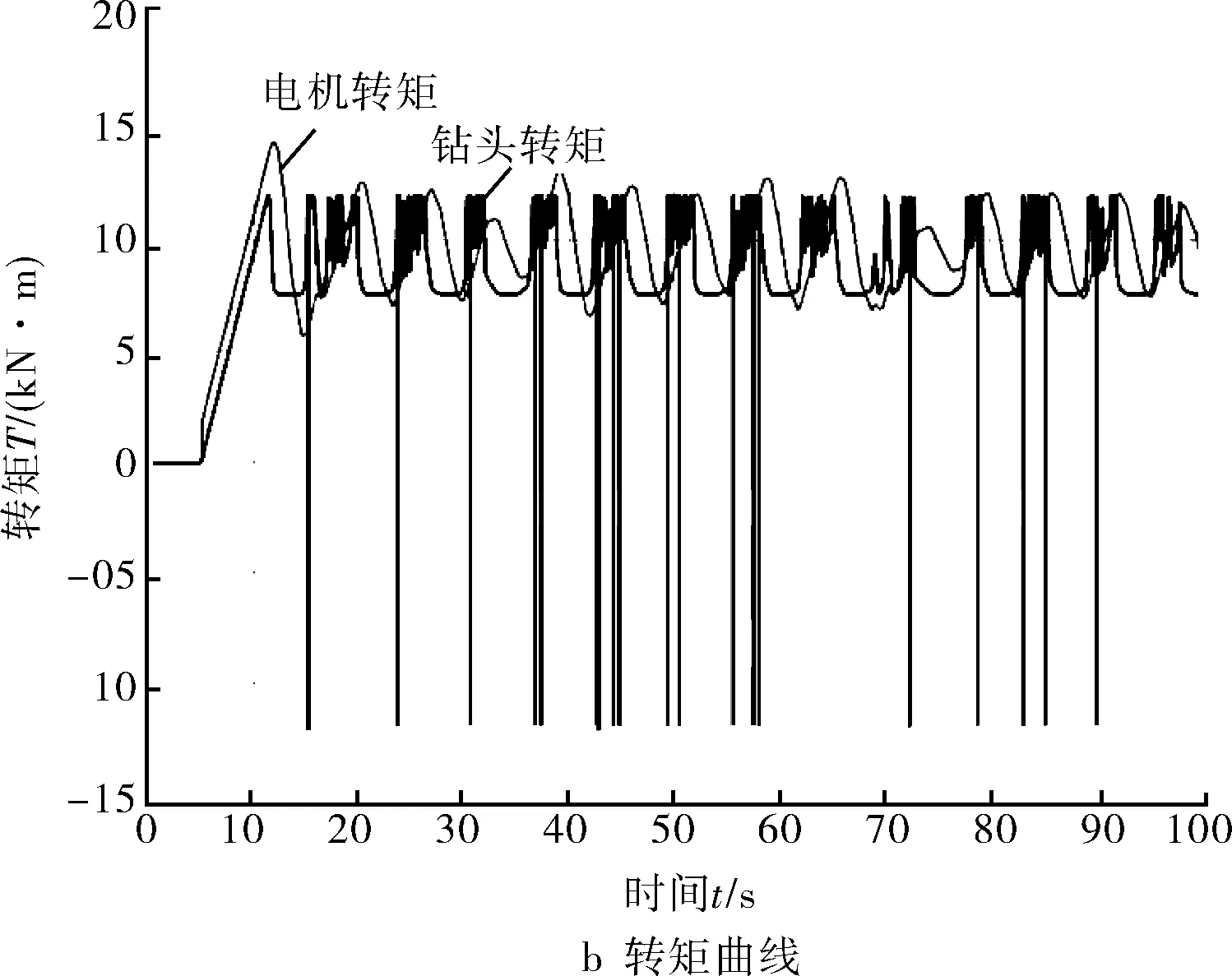
圖3 ωr=4 rad/s時轉速-轉矩仿真結果

當給定轉速值ωr=8 rad/s，仿真結果如圖4所示，鉆頭的轉速和頂驅力矩出現短期的振蕩，有粘滑現象產生。但是，隨著時間的推移，最終鉆頭鉆速與轉矩值趨于恒定，鉆頭處的轉速與頂驅轉速最終相同，說明鉆頭處的摩擦轉矩為滑動摩擦轉矩。此時系統的粘滑振動消除。結合前一組數據對比，可知增大頂驅轉速，可以減小粘滑現象。

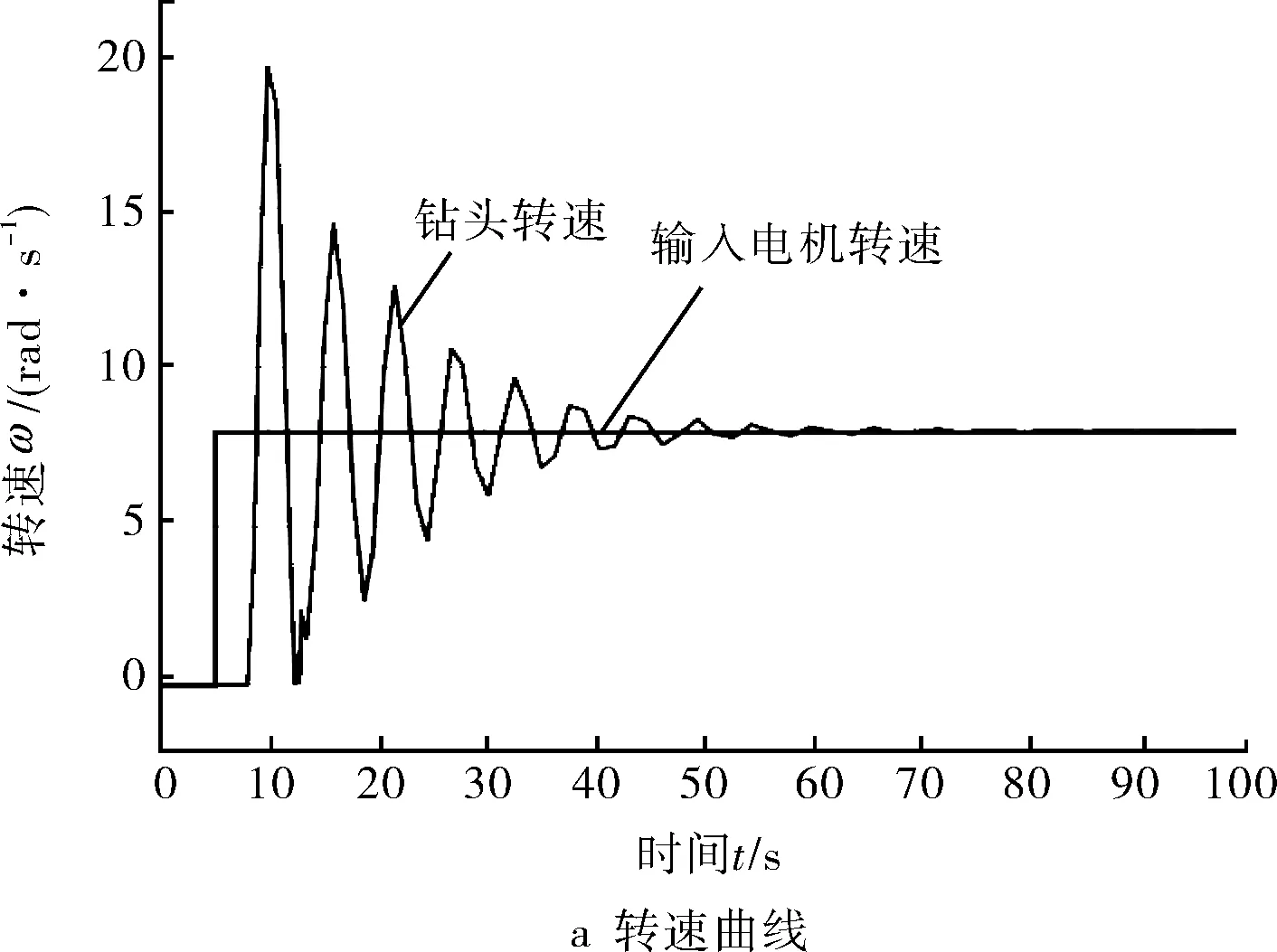
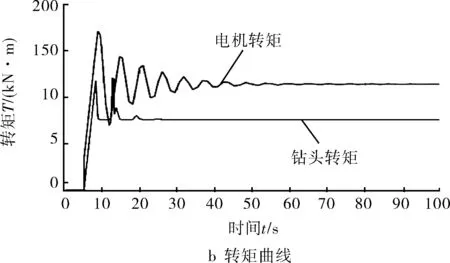
圖4 ωr=8 rad/s時轉速-轉矩仿真結果

通過對鉆柱系統簡化模型分析，結合仿真波形的規律可知：當井下的鉆桿長度超過其臨界長度，對于一定轉速，將會產生粘滑振動。減小鉆桿等效剛度系數，或增大鉆桿粘滯阻尼系數，會使粘滑振動的周期延長，振幅加大。提高頂驅轉速，或降低鉆頭鉆壓，可有效地消除粘滑振動現象。

2 PID自適應控制策略

2.1 PID控制器簡述

PID控制器是一種線性控制器，它根據給定值r(t)與實際輸出值y(t)構成控制偏差[12]，即:

e(t)=r(t)-y(t)

(8)

對于計算機處理的采樣數據來說，它是基于采樣時刻點kT的偏差值來計算控制量。在此基礎上需對偏差公式進行離散化處理。現在以采樣時刻點kT(k=0,1,2,…,n)代替連續時間t，以和式代替積分，以增量代替微分，則可做如下近似變換：

可得離散的PID表達式為：

(10)

式中：T為采樣周期，在模型計算中要使T值足夠小，且滿足香農采樣定理，方能保證系統有一定的精度；k為采樣序號，k=0,1,2,…n；e(k)為第k次采樣時刻輸入的偏差值；e(k-1)為第k-1次采樣時刻輸入的偏差值；u(k)為第k次采樣時刻計算機的輸出值[13]。

2.2 雙閉環自適應控制策略

在實際的鉆井過程中，由于井底運轉條件復雜，檢測裝置采集的信號經長距離傳輸后精度變低，鉆頭的狀態無法通過硬件檢測裝置獲取檢測信息。因此直接將鉆頭作為被控對象的雙閉環調節控制系統將無法實現預想的控制效果，必須采取其他措施對其改進。

結合前面建立的鉆柱動力學模型，依據鉆柱動力學建模中的各類參數，計算出鉆頭的速度狀態值和所受摩擦轉矩數值，反饋給頂驅電機。并且當底部鉆頭受到巖石摩擦阻力較大而產生粘滑振動時，頂驅電機的轉速和轉矩也發生相應的響應。此響應是可通過頂驅電機變頻器實測的數據。依據動力學建模的鉆頭參數與實測參數相結合得出速度的補償信號，作為雙閉環控制調節系統的反饋補償，使頂驅電機的轉速得到改變，變化的電機轉速信號傳遞給變頻器，變頻器調節電機的主軸轉矩，進而使主軸轉矩值發生變化，改變井下的運轉狀態，調節鉆柱的扭轉能量，抑制粘滑振動的產生[14]。為此，在轉矩負反饋的基礎上提出轉速-轉矩雙閉環負反饋調節控制系統。

圖5為基于PID控制的雙閉環控制策略系統圖。雙閉環的意思是具有2個閉合回路，內回路為轉矩環，稱為副回路；外回路為速度環，稱為主回路。主副回路各有調節控制器和限幅器。主回路中由檢測裝置獲取拖動電機的轉速值，乘上增益系數α，得出給定速度參數nf=α·ng，經PID控制器和限幅器輸出給轉矩給定值；而副回路中從執行器中檢測出的轉矩值Tg，乘上增益系數β，得出另一轉矩給定參數Tf=β·Tg，經PI控制器和限幅器輸出給執行器和電機。主調節器與副調節器以串級的方式進行共同控制，故稱為串級聯動控制系統。由于主調節器的輸出作為副調節器的給定值，因而串級控制系統的主回路是1個恒值控制系統，而副回路可以看作是1個隨動系統。串級控制系統在結構上比單回路控制系統多了1個副回路，因而對進入副回路的二次擾動有很強的抑制能力[15-16]。

圖5 雙閉環控制策略系統框圖

2.3 雙閉環控制效果圖

由上文所述的雙閉環控制策略，在Simulink仿真軟件上畫出仿真框圖，如圖6所示。

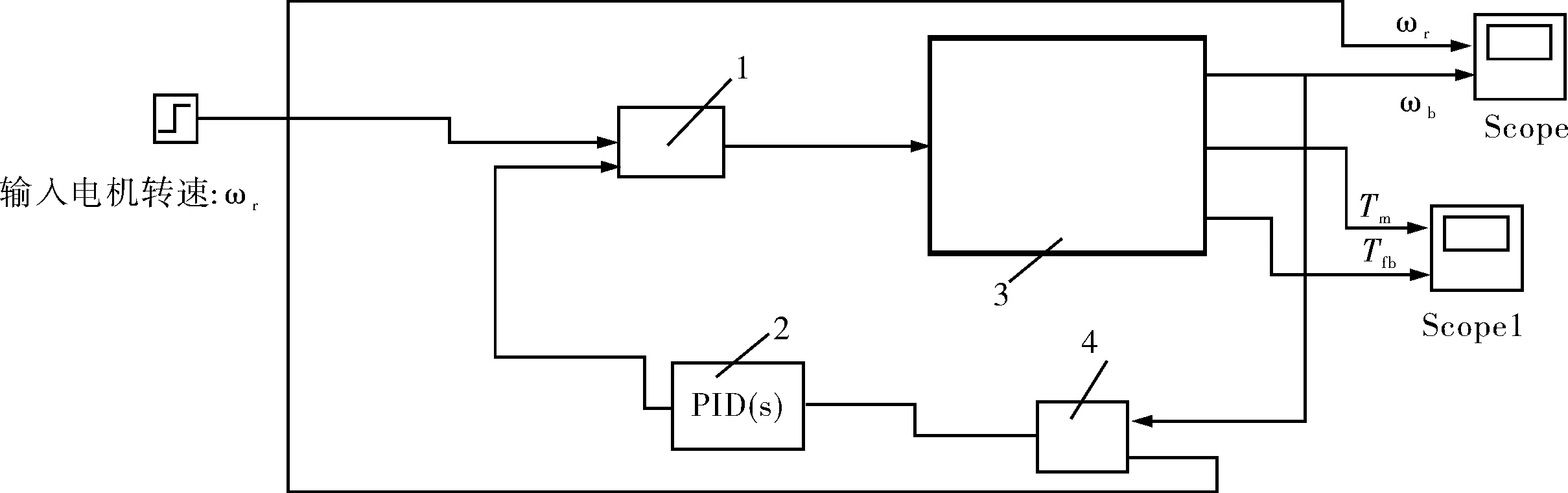
1-積分調節角速度差；2-PID控制器；3-鉆柱動力學系統；4-初始角速度差。圖6 PID控制建模仿真框圖

當選取PID控制策略，設定參數P=2.1,I=0,D=0時，鉆頭的轉速和轉矩值的變化曲線如圖7所示，可知，在3～4個周期內，轉速和轉矩值均趨于平穩狀態，說明以輸出的鉆頭轉速作為檢測值，與給定轉速作差作為PID控制器的輸入端，得到的最終偏差值加到給定的頂驅轉速上，使頂驅電機輸出調整的速度波形，可以有效地消除粘滑振動現象。但細微地觀察會發現，鉆頭的轉速和轉矩值會有輕度的波動，這是源于單個P值引起的調整振蕩。

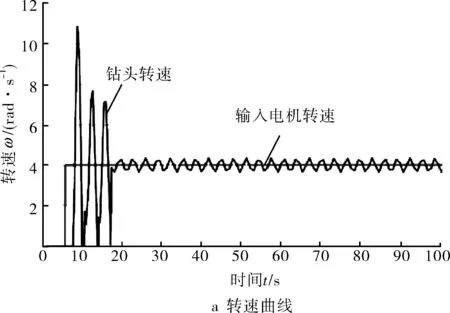
圖7 轉速-轉矩仿真結果(P=2.1,I=0,D=0)

當選取P=2.1,I=0,D=0.8時,軟轉矩控制效果如圖8所示，可知，鉆頭鉆速和轉矩可以很快達到控制效果，而且消除了調整單個P值引起的振蕩現象，此種情況為控制的理想狀態，從另一方面也驗證了PID控制策略的可行性與優越性。

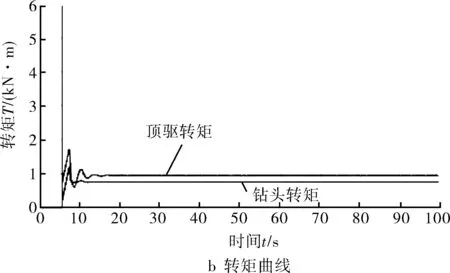
圖8 轉速-轉矩仿真結果(P=2.1,I=0,D=0.8)

3 結論

1) 本文闡明了鉆柱粘滑振動產生機理。建立了二自由度的鉆柱動力學模型，得出鉆頭的狀態方程，并仿真出粘滑時的鉆頭狀態曲線。

2) 基于頂驅電機轉速與鉆頭轉速的函數關系，提出轉速-轉矩雙閉環調節控制策略，并由仿真結果驗證了控制策略的可行性。綜合試驗結果表明，反饋調節的頂驅轉速能夠在3～5個周期內有效地抑制鉆柱粘滑振動。