大跨徑中承式鋼拱橋索拱及索梁連接構造設計及局部受力分析
李科 王琪 鄭愛華



摘要:吊桿拱橋的索拱、索梁錨固區是整個橋梁荷載傳遞體系的關鍵節點,構造復雜且力學性能要求高,文章以一座大跨徑中承式吊桿鋼桁架拱橋為研究對象,對該橋索拱、索梁錨固構造進行了局部精細化有限元計算分析。計算結果顯示,該部分構造設計滿足規范要求,且有一定的安全儲備。
[作者簡介]李科(1989—),男,碩士,工程師,主要從事大跨度橋梁及復雜景觀橋梁設計工作;王琪(1983—),男,本科,高級工程師,主要從事市政工程設計管理工作;鄭愛華(1977—),男,本科,高級工程師,主要從事復雜結構的景觀橋梁、大跨度橋梁設計工作。
對于中、下承式拱橋,吊桿是將橋面荷載傳遞給拱肋的主要構件。吊索-主梁節點以及吊索-拱肋節點的構造復雜且力學性能要求高,是設計時需要重點考慮和分析的對象,結合具體工程的特點存在有若干種做法:有采用鋼錨箱形式[5、8]、銷鉸耳板形式[7]、齒塊錨固[11]、錨拉板形式、鋼錨管形式等。其中,李若思等[13]研究了鋼錨箱和吊耳形式在同一個工程中受力的優缺點;易達等[9]研究了豎直吊耳和斜吊耳的對拱內構造和受力的影響,具有參考價值。
1 工程概況
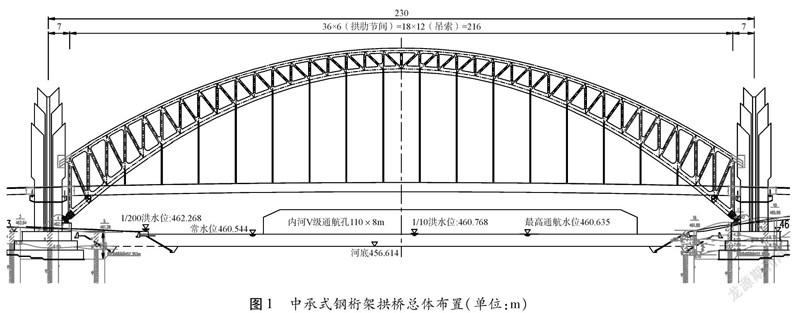
天保灣大橋位于成都市天府新區直管區沈陽路西段,橫跨錦江。主橋長230 m,為一孔中承式鋼桁架兩鉸拱橋(圖1),橋面布置形式為: 3.5 m人行道+3.5 m輔道+0.25 m欄桿+2.5 m拱肋保護區+0.5 m隔離帶+11.25 m機動車道+0.5 m中央隔離護欄+11.25 m機動車道+0.5 m隔離帶+2.5 m拱肋保護區+0.25 m欄桿+3.5 m輔道+3.5 m人行道=43.5 m。
全橋橫橋向設置兩片拱肋。拱肋上弦桿軸線采用二次拋物線,計算跨徑L1=216 m,計算矢高f1=35 m,矢跨比f1/L1=1/6.17;拱肋下弦桿軸線采用二次拋物線,計算跨徑L2=216 m,計算矢高f2=49 m,矢跨比f2/L2=1/4.41。主拱上弦桿末端伸入橋頭堡預埋橫向限位裝置,下弦桿拱腳處采用鑄鋼鉸與拱座預埋件連接。
鋼加勁梁采用雙箱單室形式,箱體寬2 m,中心梁高2.801 m,兩箱之間設置縱橋向間距3 m 的工字鋼橫梁,梁高2.674~3 m。橋面采用正交異性板鋼橋面板。全橋共設置16對吊桿,拱上吊桿間距12 m,除端部短吊桿采用剛性吊桿外,其余均為柔性吊桿。
2 索拱、索梁構造設計
2.1 索拱構造
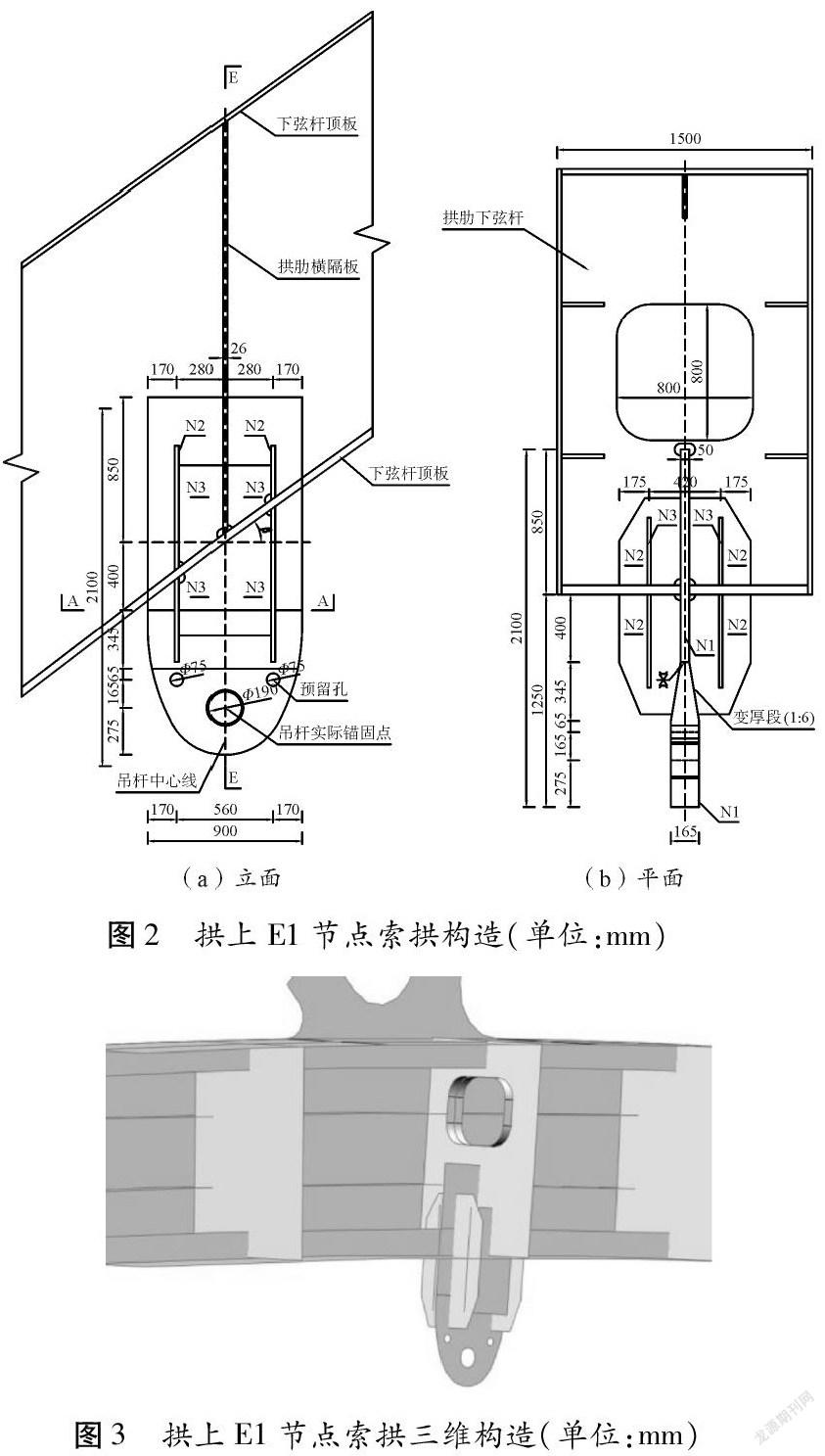
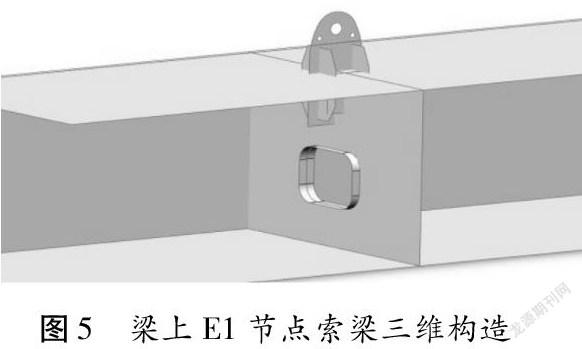
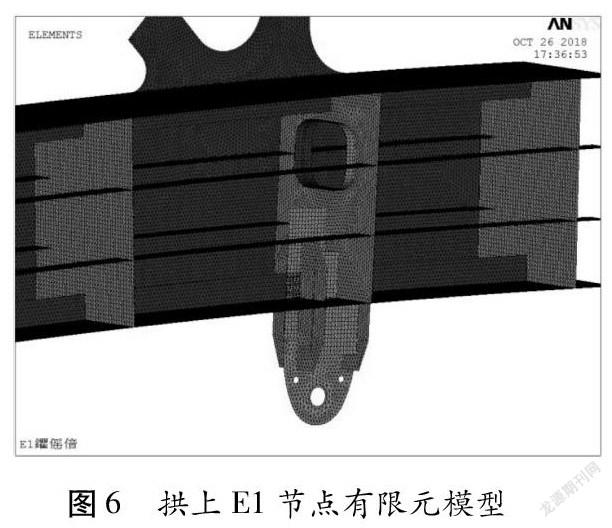
以天保灣大橋拱上E1節點(拱頂位置)為例,吊耳(N1)呈90°與拱上橫隔板正交,插入拱肋,耳板(N1)設置兩塊平行于拱肋橫隔板的八邊形加勁板(N2),同時平行于耳板設置兩塊承拉板(N3)(圖2、圖3)。
2.2 索梁構造
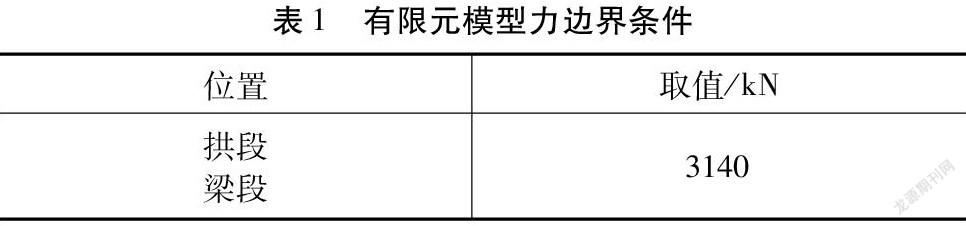
以天保灣大橋梁上E1節點為例,吊耳(N1)呈90°與梁體橫隔板正交,嵌入梁體,耳板(N1)設置兩塊平行于梁肋橫隔板的八邊形加勁板(N2),同時平行于耳板設置兩塊承拉板(N3)(圖4、圖5)。
3 計算分析
3.1 荷載
應力邊界條件由整體計算所得的荷載決定, 邊界力采用剛性耦合面節點力施加。通過Midas/Civil 2017有限元軟件建立主橋整體模型,獲得承載能力極限狀態下拱梁及索梁位置的吊桿力(表1)。
3.2 有限元模型
本文進行梁上及拱上錨點局部應力分析[1-4]時,索梁、索拱錨固區[9-10]局部受力情況,參照圣維南原理[7]計算梁段長度,且應保證錨點附近范圍內的腹板應力受邊界條件影響較小,因此取2倍梁高范圍[6]。
鐵路與公路李科, 王琪, 鄭愛華: 大跨徑中承式鋼拱橋索拱及索梁連接構造設計及局部受力分析研究由于吊桿錨固區構件多,空間位置關系復雜,建模工作量大,所以本文采用Solidworks建立三維模型,采用ANSYS的APDL參數化設計語言提高建模效率,便于修改和調整模型。鋼板采用Shell63殼單元模擬。吊耳加載點采用Mass21質量單元模擬。
3.3 局部應力分析
3.3.1 索拱模型應力分析
建立有限元模型見圖6。
加載節點吊桿力后的結果如圖7所示。
從圖7可以看出應力傳遞趨勢為通過耳板(N1),將索力傳遞到主拱下弦桿底板和橫隔板,然后將力擴散至全拱,主拱下弦桿底板承受面外應力,橫隔板承受面內拉應力為主。橫隔板局部最大應力182 MPa。耳板應力70.1 MPa,N2板件68 MPa,N3板件87 MPa,底板144 MPa,橫隔板123 MPa。
3.3.2 索梁模型應力分析
從拱上應力狀態可知,加勁肋對此類節點模型應力水平影響不大,因此為簡化計算,梁上有限元模型建模時不考慮加勁肋影響。
建立有限元模型如圖8所示。
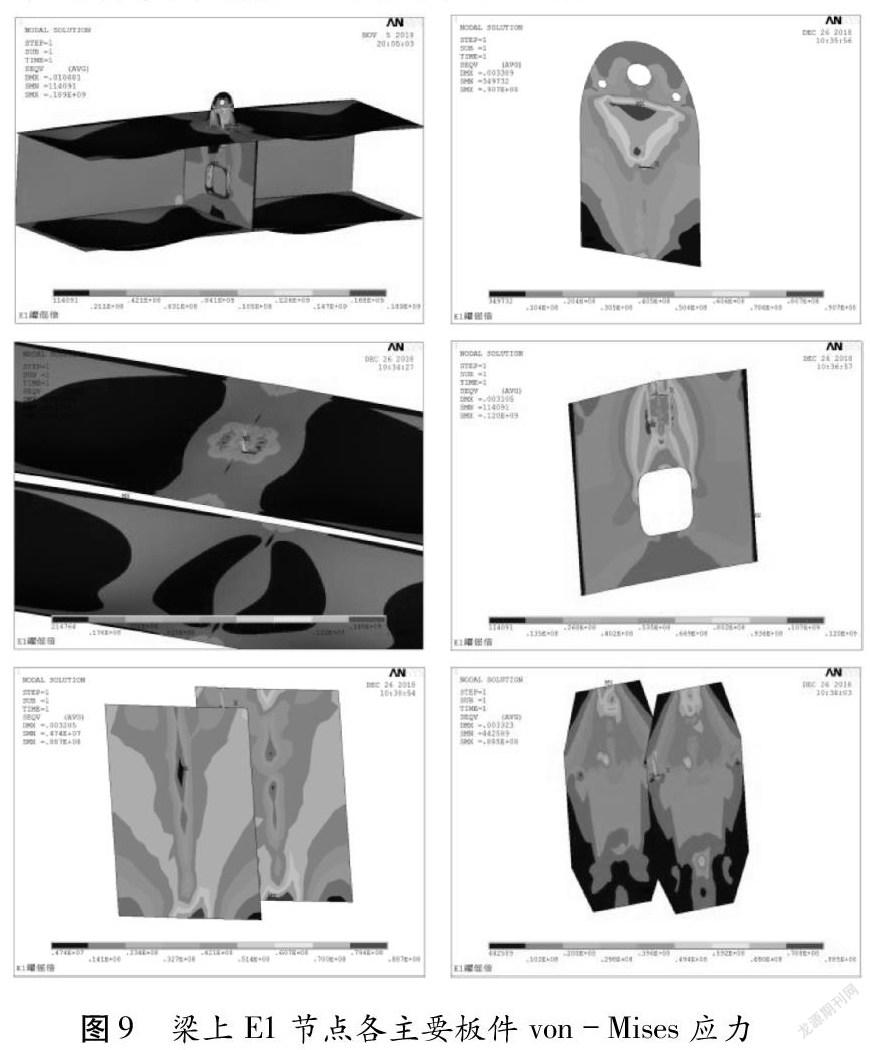
加載節點吊桿力后的結果如圖9所示。
從上圖可以看出應力傳遞趨勢為:主橋橋面承受的荷載通過橫隔板傳遞到耳板,主梁頂底板承受面外應力,橫隔板承受面內拉應力為主。橫隔板局部最大應力189 MPa。耳板應力90.7 MPa,N2板件88 MPa,N3板件88.7 MPa,頂板157 MPa,橫隔板120 MPa。
4 結論
(1)索拱連接部位最大應力不超過182 MPa,索梁連接部位最大應力不超過189 MPa,均出現在橫隔板,說明該板件為重要直接傳力結構,設計中應該注重該位置強度。
(2)主梁索梁連接的傳力途徑為:主橋橋面承受的荷載通過橫隔板傳遞到耳板,主梁頂底板承受面外應力,橫隔板承受面內拉應力為主。
主拱索拱連接的傳力途徑為: 應力傳遞趨勢為通過耳板,將索力傳遞到主拱下弦桿底板和橫隔板,然后將力擴散至全拱,主拱下弦桿底板承受面外應力,橫隔板承受面內拉應力為主。
(3)索梁、索拱構造的橫隔板的厚度對局部應力控制起到了直接作用,加強與吊耳連接橫隔板的構造是有效的,對后續同類橋梁設計起到參考意義。
參考文獻
[1] 程玉芹, 王朝, 劉昆. A形吊耳強度有限元分析[C]// 達索系統2013 SIMULIA中國區用戶大會. 2013.
[2] 肖文勇, 佘凱. 吊耳局部有限元建模技術分析[J]. 船舶工程, 2009, 31(s1):94-97.
[3] 劉淼. 鋼管混凝土斜拉橋索塔鋼錨箱受力分析及優化[J]. 建設科技, 2018(2):106-107.
[4] 桂水榮, 陳水生, 萬水. 系桿拱橋吊桿節點足尺模型承載性能試驗研究[J]. 橋梁建設, 2013, 43(2):58-63.
[5] 黃智華. 自錨式懸索橋鋼錨箱設計及受力分析[J]. 城市道橋與防洪, 2017(12):44-46.
[6] 高小妮, 賀拴海, 趙煜. 索梁錨固區應力狀態單因素影響分析[J]. 廣西大學學報(自然科學版), 2012, 37(1):94-102.
[7] 劉琛. 138m鋼箱疊拱橋耳板錨固結構應力分析[J]. 鐵道標準設計, 2014, 58(7):98-101.
[8] 鄭綱, 王天亮. 獵德大橋吊索錨箱傳力和疲勞性能試驗方案設計[J]. 世界橋梁, 2009, 2009(1):49-52.
[9] 易達. 大跨度鋼桁架拱橋地震響應分析和索拱連接詳細應力分析和結構優化[D]. 成都:西南交通大學, 2016.
[10] 黃利鋒, 馮健, 趙建,等. 內凹式索拱結構極限承載力研究[J]. 建筑結構學報, 2010, 31(2):41-47.
[11] 盧元剛, 王勝男. 部分斜拉橋索梁錨固區應力分析[J]. 工程與建設, 2015, 29(6):18-20.
[12] 王曉明, 袁遠, 郝憲武. RC系桿拱橋拱肋吊桿錨固結構力學性能分析與優化[J]. 鐵道建筑, 2013(7):8-9.
[13] 李若思. 鋼箱提籃拱橋使用階段的詳細應力分析及地震響應分析[D]. 成都:西南交通大學, 2018.

