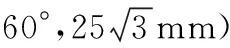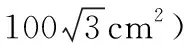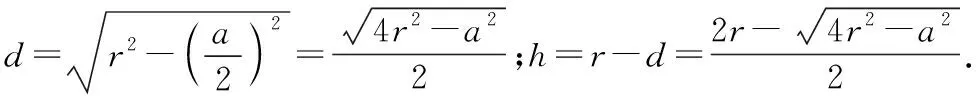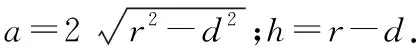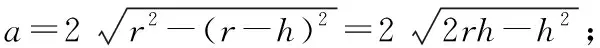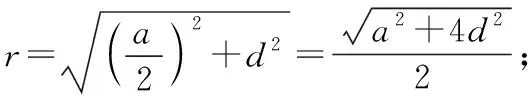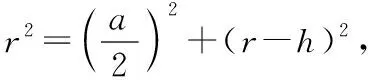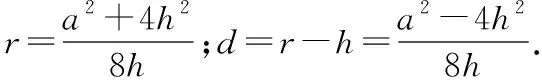深入題目本質，避免題海戰術系列談之一
——垂徑定理及其推論的應用小妙招

◎姜秀敏 (吉林省白山市第九中學，吉林 白山 134300)

我常常思考這樣的問題：學數學一定要多做題才能學好嗎？如何讓學生不采用“題海戰術”也能學好數學？我認為，弄清楚題目的本質是不搞“題海戰術”也能學好數學的途徑.下面，我以垂徑定理及其推論的相關應用題的解題規律為例，淺談上述問題.

簡單說，此類題大多數需要作輔助線來解決，學生只需要作輔助線構造“一個那樣的直角三角形”，再應用垂徑定理及其推論和勾股定理，就可解題了.因此，學生只要記住如何作出“一個那樣的直角三角形”，就能解決大部分此類問題，達到事半功倍的效果.

下面舉兩個例子說明.

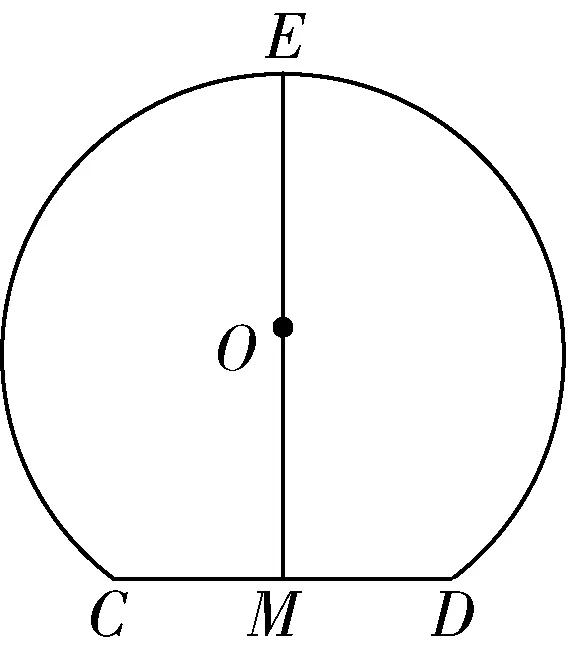
例1 (人教版教材九上90頁12題)，如圖1，一條公路的轉彎處是一段圓弧(圖1中的弧ACB)，點O是這段弧所在圓的圓心，AB=300 m，C是這段弧上一點，OC⊥AB，垂足為D，CD=45 m，求這段彎路的半徑.

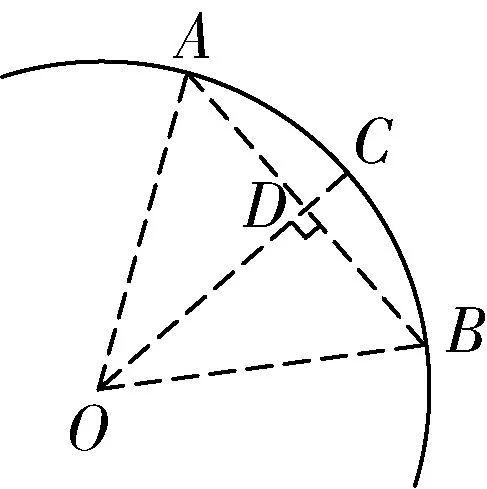
圖1

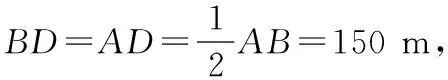
詳解：∵OC⊥AB，

由垂徑定理得

設這段彎路的半徑為xm，

則OA=OC=xm，OD=OC-CD=(x-45)m，

在Rt△AOD中，

由勾股定理得

OD2+AD2=OA2，

∴(x-45)2+1502=x2，

解得x=272.5，

答：這段彎路的半徑是272.5 m.

點撥：此題主要考查了垂徑定理及勾股定理等知識.在作出輔助線(本題的輔助線書中已給)構造“一個那樣的直角三角形”后，利用勾股定理列式計算即可解決問題.

“一個那樣的直角三角形”究竟是什么三角形？下面具體闡述.結合圖1可以看到，“一個那樣的直角三角形”是由以下三條邊構成的：斜邊是圓的半徑，一條直角邊是弦長的一半，另一條直角邊是弦心距.本例啟發我們，今后遇到有關垂徑定理及其推論的題目時，可以優先嘗試采用作輔助線構造“一個那樣的直角三角形”的方法，通過垂徑定理及勾股定理解決問題.

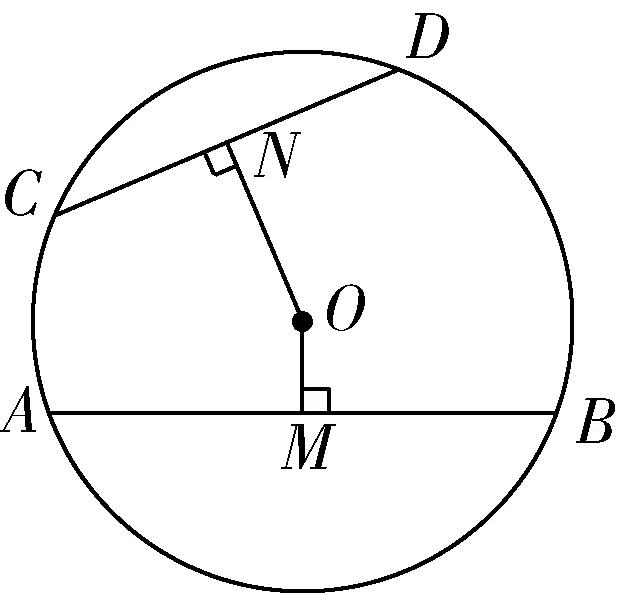
例2 (人教版教材九上91頁15題改編)求證：弦越長，弦所對的弦心距越短，反之也成立.

簡析：大家都知道，此類題目要結合問題敘述作出符合要求的圖形，先根據命題的題設和結論寫出已知和求證，然后進行證明.

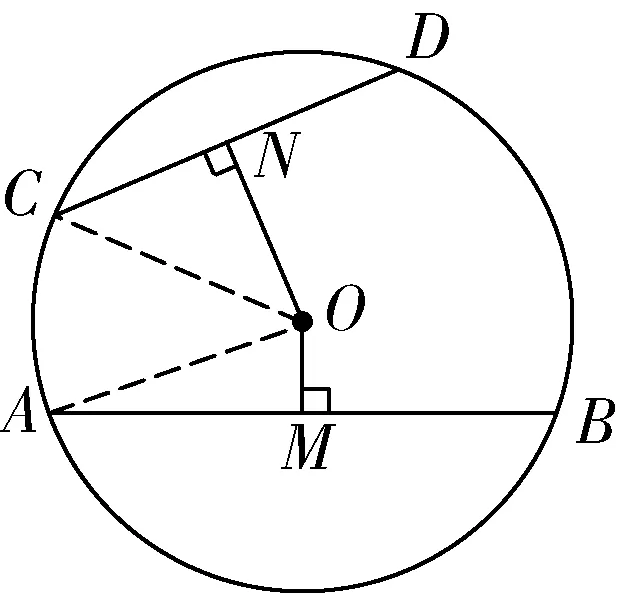
詳解：

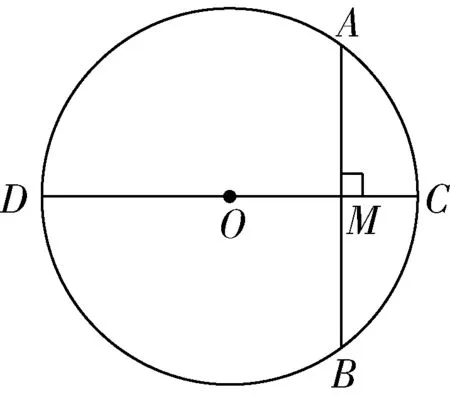
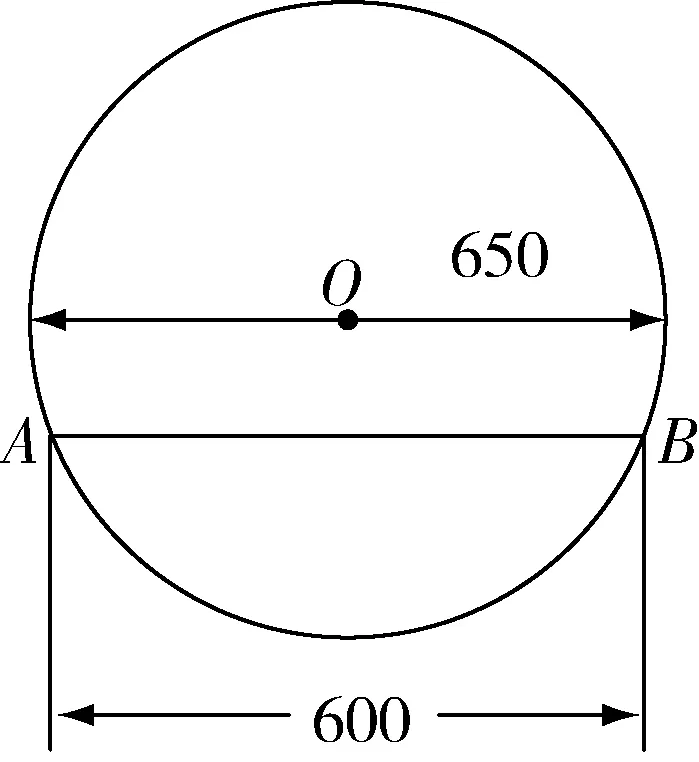
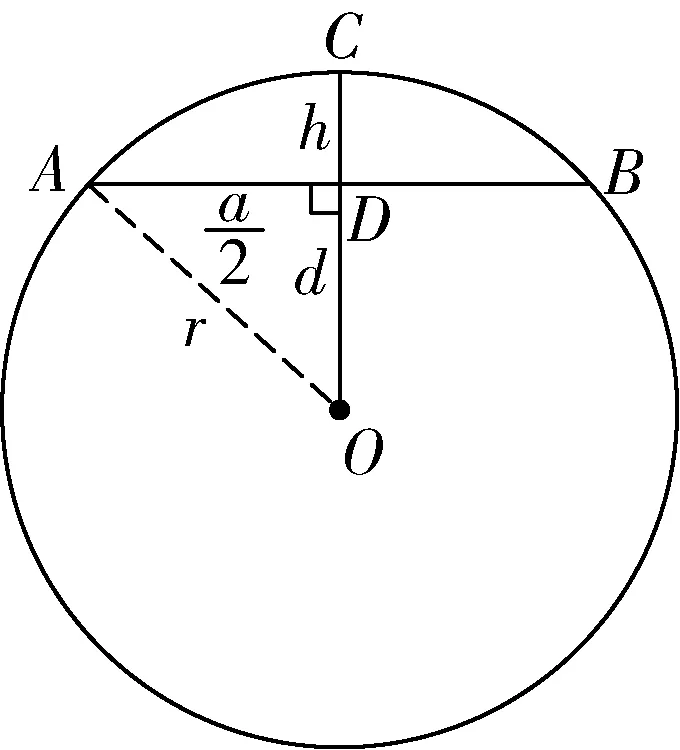
已知：如圖2，在⊙O中，有兩條弦AB，CD，且AB>CD，過O點分別作OM丄AB于M，ON⊥CD于N.

求證：OM

圖2

證明：分別連接OA，OC，設⊙O的半徑為r，如圖3.

∵OM丄AB，ON⊥CD，

由垂徑定理得

又∵AB>CD，

∴AM>CN，

∴AM2>CN2.

在Rt△OAM和Rt△OCN中，

由勾股定理得

又∵AM2>CN2.

∴OM

顯然，逆推回去也成立.

圖3

點撥：本題作輔助線構造了“一個那樣的直角三角形”，再利用垂徑定理和勾股定理進行OM與ON長度的比較，使問題最終得到解決.

下面給出教材中的7個練習題，均可采用上文介紹的解題方法解決.

練習題1.(人教版教材九上83頁1題)如圖4，在⊙O中，弦AB的長為8 cm，圓心O到AB的距離為3 cm，求⊙O的半徑.

圖4

(答案：5 cm)

練習題2.(人教版教材九上89頁2題)如圖5，在半徑為50 mm的⊙O中，弦AB的長為50 mm，

圖5

(1)求∠AOB的度數；

(2)求點O到AB的距離.

練習題3.(人教版教材九上89頁3題)如圖6是一個隧道的橫截面，它的形狀是以點O為圓心的圓的一部分.如果M是⊙O中弦CD的中點，EM經過圓心O交⊙O于點E，并且CD=4 m，EM=6 m，求⊙O的半徑.

圖6

練習題4.(人教版教材九上90頁10題)已知⊙O的半徑為13 cm，弦AB∥CD，AB=24 cm，CD=10 cm，求AB和CD之間的距離.

(答案：AB與CD之間的距離為7 cm或17 cm.)

練習題5.(人教版教材九上122頁1題)如圖7，⊙O的直徑CD=10 cm，AB是⊙O的弦，AB⊥CD，垂足為M，OM∶OC=3∶5，則AB的長為( ).

圖7

C.6 cm D.4 cm

(答案：B)

練習題6.(人教版教材九上123頁3題)如圖8，AB是⊙O的弦，半徑OA=20 cm，∠AOB=120°，求△AOB的面積.

圖8

練習題7.(人教版教材九上124頁10題)在直徑為650 mm的圓柱形油槽內裝入一些油后，截面如圖9所示，若油面寬AB=600 mm，求油的最大深度.

圖9

(答案：200 mm)

從以上的例題和練習題可以看出，垂徑定理及其推論在解某一類型題時十分有效，這一解題方法揭示了問題的本質.

如圖10，已知，⊙O的半徑為r，弦AB=a，弦心距OD=d，拱高CD=h.在r、a、d、h這四個量中，任意知道兩個量就可以引輔助線構造“一個那樣的直角三角形”，然后利用垂徑定理及其推論，結合勾股定理求出另外兩個量，即“知二求二”，現分述如下.

圖10

d=r-h.

以上六個結論不需要死記硬背，只需要記住解題思路即可.可以肯定地講，如果學生將本文列舉的這些例題、練習題都理解、會做，那么再遇到這類題時，就完全有能力快速解決了.