圓柱矢量波函數(shù)的構(gòu)建及其在圓柱波導(dǎo)中的應(yīng)用
雒向東,海 波,趙宇杰,梁 曄
(1.蘭州城市學(xué)院 電子工程學(xué)院,甘肅 蘭州 730070; 2.《甘肅高師學(xué)報》編輯部,甘肅 蘭州 730070;3.蘭州城市學(xué)院 信息工程學(xué)院,甘肅 蘭州 730070)
0 引言
近幾十年來,自Hansen首次引進矢量波函數(shù)來解決某些電磁場問題[1-3],Stratton驗證了這些函數(shù)的有效性[4],這些函數(shù)的使用方法進一步被Stratton、Morse、Feshbach等人推廣[5],戴振鐸、宋文淼、魯述等就電磁理論中的并矢格林函數(shù)(DGF)也做了大量的研究[6-13],使得DGF方法被廣泛地應(yīng)用于電磁理論及工程的各個領(lǐng)域。毫無疑問,DGF現(xiàn)已成為電磁理論中的一個重要概念和解決問題的方法。用DGF方法解決各種電磁場工程問題,其關(guān)鍵在于求出DGF表達關(guān)系,因此DGF的研究和求解自然成為人們關(guān)注的熱點問題。由于不同的正交曲線坐標(biāo)系的本征波函數(shù)的展開各有特殊性,使得DGF研究具有復(fù)雜性,國內(nèi)外學(xué)者對此均作了大量研究,如對規(guī)則形狀波導(dǎo)、常用坐標(biāo)系等問題已形成較一致的意見。但有些問題,如柱坐標(biāo)系中的本征展開問題仍存在爭議,對該問題的報道也比較少[14-18]。本文就圓柱波導(dǎo)DGF的構(gòu)建、正交歸一性質(zhì)及其在圓柱波導(dǎo)中的應(yīng)用做了詳細研究,其研究結(jié)論可為基于DGF方法解決電磁場工程等問題提供理論和技術(shù)支持。
1 構(gòu)建具有離散本征值的圓柱矢量波函數(shù)
1.1 圓柱坐標(biāo)系中的標(biāo)量波函數(shù)
建立如圖1所示的圓柱波導(dǎo)示意圖。圓柱截面半徑為a,坐標(biāo)變量用r、φ、z來表示。用pnm和qnm分別表示整階貝塞爾函數(shù)Jn(x)和該函數(shù)微商J′n(x)的根。
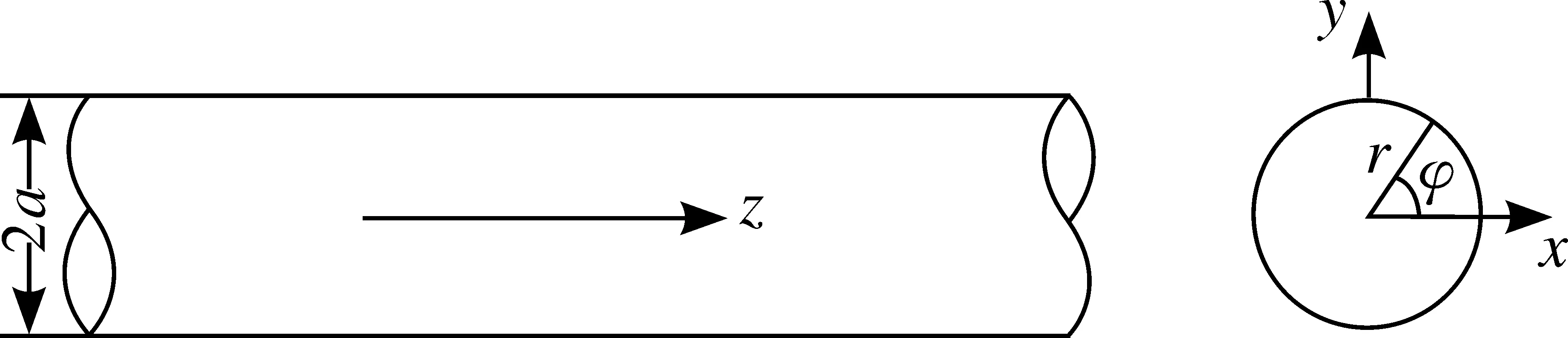
圖1 圓柱波導(dǎo)示意圖
首先研究齊次標(biāo)量亥姆霍茲方程,從而得到柱坐標(biāo)系的標(biāo)量波函數(shù)。用分離變量法解標(biāo)量波動方程:
(1)
(2)
設(shè)式(2)的解為:
Φ(r,φ,z)=R(r)Φ(φ)Z(z)。
(3)
對式(3)分離變量,得出的4個分量方程為:
Φ″+n2Φ=0,
(4)
(5)
(6)
(7)
式(4)和式(5)中的Φ和Z的解為諧函數(shù),可能的取值分別為:
cosnφ,sinnφ,einφ,e-inφ(n=0,1,2,3,…),
(8)
coshz,sinhz,eihz,e-ihz。
(9)
式(6)中,R是n階貝塞爾函數(shù),方程解的形式為:
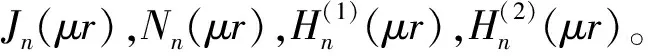
(10)
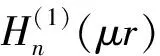
(11)
或者可寫成:
(12)
式(12)中,“+”表示沿z反方向傳播的波,“-”表示沿z正方向傳播的波,下標(biāo)e、o分別表示函數(shù)為偶函數(shù)和奇函數(shù)。在圓波導(dǎo)內(nèi),假設(shè)波沿z軸方向?qū)校卅铡方向均為駐波,其基本波函數(shù)可表示為[19]:
(13)
式(13)中,除n=0的情況外,每一組分離常數(shù)對應(yīng)兩種不同極化場的模式,稱為模式的極化簡并。
1.2 圓柱坐標(biāo)系中的矢量波函數(shù)
基于圓柱坐標(biāo)系中的標(biāo)量波函數(shù),定義兩類圓柱矢量波函數(shù),它們在r=a時都滿足矢量狄里克雷邊界條件。
兩類圓柱矢量波函數(shù)定義為[6]:

(14)
其中,
(15)
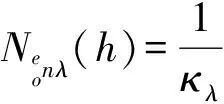
(16)
其中,
(17)
兩組矢量波函數(shù)的全表達式為:
(18)
(19)
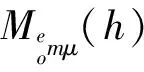
描述圓柱波導(dǎo)中的磁場,可采用的矢量波函數(shù)為:
(20)
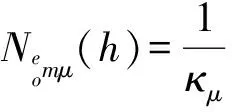
(21)
函數(shù)M(h)和N(h)滿足下列關(guān)系[6]:
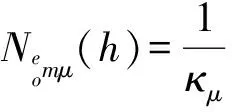
(22)
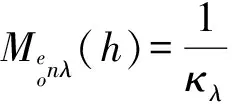
(23)
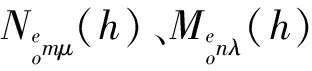
1.3 圓柱坐標(biāo)系中矢量波函數(shù)的正交歸一性
圓柱矢量波函數(shù)具有正交性,可舉例證明如下:
(24)
要證明式(24)正交關(guān)系成立,首先討論下面積分:
(25)
將式(18)及(19)代入式(25)可得:
e-i(h-h′)zdV。
(26)
第一種情形:
(27)
(28)
第二種情形:
(29)
(30)
這兩種情形推證中都應(yīng)用了以下公式[6]338:
(31)
在以上兩種情況的推證中,由于Jn(λa)=0,故I1=I2=0,所以有:
(32)
矢量波函數(shù)正交歸一關(guān)系總結(jié)如下(不再證明):
(33)
(34)
(35)
式(34)和(35)中,δ0表示對n的克羅內(nèi)克δ函數(shù)。式中體積分是對無限長波導(dǎo)的整個區(qū)域的積分,當(dāng)n≠n′時,在φ域中所有圓柱矢量波函數(shù)都是正交的,這些正交關(guān)系這里不再證明。
2 圓柱波導(dǎo)的并矢格林函數(shù)
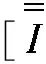
(36)
式(36)中,求和指數(shù)m、n與關(guān)系式pnm=λa和qnm=μa相聯(lián)系,上式可簡化記為:
(37)
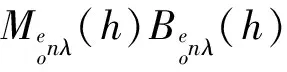
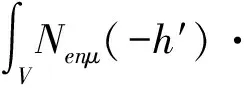
Nenμ(-h′)·Menλ(h)Benλ(h)]dV,
(38)
(39)
用Nonμ(-h′)、Menλ(-h′)和Monλ(-h′)分別與式(36)作前標(biāo)積,同樣可分別求得其系數(shù)為:
(40)
(41)
(42)
四個系數(shù)可簡寫為:

(43)
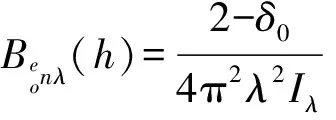
(44)
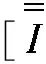
(45)
假設(shè)磁型并矢格林函數(shù)為:
(46)
將式(45)和(46)代入DGF滿足的麥克斯韋方程[20]:
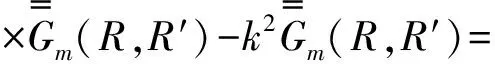
(47)
求解系數(shù)得:
(48)
(49)
將系數(shù)表達式(48)和(49)代入式(46)得:
(50)
用圍線積分法計算[21],對TE模當(dāng):
(51)
根據(jù)式(50)解得:
(52)
對TM模,當(dāng):
(53)
根據(jù)式(50)解得:
(54)
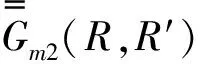
(55)
式(55)中上行符號對應(yīng)z>z′,下行符號對應(yīng)z (56) 式(56)中,kμ、kλ表示兩組模式相應(yīng)的導(dǎo)波函數(shù)。 (58) δ(r-r′)=δ(ρ-ρ′)δ(φ-φ′), (59) (60) (61) (62) 式(62)中使用了兩個單位階躍函數(shù)為: (63) (64) 進一步推導(dǎo)得: (65) 由廣義函數(shù)理論知: ?U(z-z′)=ezδ(z-z′), (66) ?U(z′-z)=-ezδ(z-z′)。 (67) 將式(66)、式(67)代入式(65)得: (68) 利用式(60),式(68)又可寫成: (69) 式(69)對于所有ρ,φ,z值都適用,由于下式成立: δ(ρ-ρ′)δ(φ-φ′)δ(z-z′)=δ(R-R′)。 (70) 把式(69)和式(70)代入式(61)得: (71) 將式(55)代入式(71)得圓柱波導(dǎo)第一類電型DGF為: (72) 利用分離變量法獲得圓柱坐標(biāo)系中的標(biāo)量波函數(shù),進而研究圓柱系中的矢量波函數(shù),部分地證明這些函數(shù)的正交歸一化性質(zhì),利用這些性質(zhì)并借助Ohm-Rayleigh方法詳細推證圓柱坐標(biāo)系中圓柱波導(dǎo)的第一類電型并矢格林函數(shù)關(guān)系,利用此關(guān)系并借助第一、二類電型并矢格林函數(shù)對稱關(guān)系獲得第二類電型并矢格林函數(shù),這些電型并矢格林函數(shù)對解決在圓柱波導(dǎo)壁上用開口孔徑場激勵的波導(dǎo)內(nèi)場等問題可提供理論依據(jù)和指導(dǎo)方法[22]。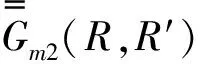
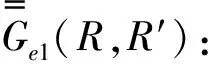
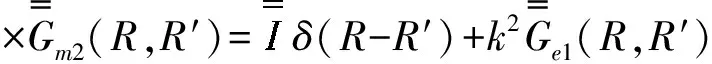
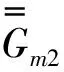
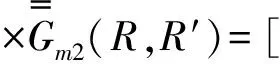

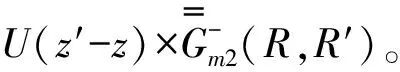
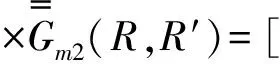
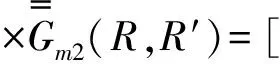
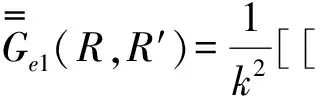
3 結(jié)語

