基于數據驅動的磁浮列車懸浮系統參數整定

溫 韜 ，夏文韜 ，周 旭 ，龍志強

（國防科技大學智能科學學院，湖南 長沙 410073）

磁浮列車是一種新制式的軌道交通系統，不同于傳統的輪軌式列車，磁浮列車同軌道間是無接觸的，列車車體依靠電磁力懸浮于軌道上方，該種制式列車具有安靜舒適等優點.

磁浮列車的懸浮系統是保障列車安全和高質量運行的關鍵系統.在磁浮列車從主機廠組裝首次投入運營時，以往通常需要根據懸浮系統數學模型來設計控制器，并整定好控制器參數，使懸浮系統能夠高質量工作，穩定懸浮.實際工作中，常結合技術人員經驗和現場試驗的方法來整定控制器參數，這項工作需要耗費大量的時間和成本.此外，當懸浮系統長時間工作以后，由于在復雜工況下受到不確定擾動等因素，系統模型參數變化，控制性能退化，情況嚴重的可能會導致列車運行出現故障，此時，也必須要重新辨識被控對象數學模型，設計控制器，并整定控制器參數.由于磁浮列車的懸浮系統模型復雜，并且模型信息無法精確獲取，因此控制器參數的整定將給磁浮列車懸浮系統的維護帶來高昂的成本負擔[1].

為了解決上述問題，開展了大量的數據驅動的控制器參數整定方法研究.例如迭代反饋整定[2-3]、虛擬參考反饋整定[4-5]、虛擬參考迭代整定[6]和基于非迭代相關的整定[7].這些方法根據系統的輸入輸出數據來調整控制器參數，避免了系統被控對象的模型辨識這一復雜工作[8-10].但是基于數據驅動的控制器參數整定方法存在以下問題：文獻[11]基于閉環響應數據有限沖激響應估計的控制器整定方法，根據被控對象的輸入輸出數據，通過估計被控對象的有限脈沖響應（FIR）模型實現控制器參數的調整，然而該方法不能實現對不穩定被控對象FIR模型的估計；文獻[12]基于虛擬時間響應的迭代增益控制器整定方法，根據單次實驗數據，結合離散時間傅里葉變換，計算閉環系統的虛擬時間響應，從而整定控制器參數，但是該方法需要長時間的數據采集.

本文提出一種數據驅動的磁浮列車懸浮系統參數整定方法，該方法能夠僅根據懸浮系統單次懸浮調試的輸入輸出數據來整定控制器參數，而無需懸浮系統的模型信息；通過引入虛擬信號來估計具有非最小相位或不穩定控制器的閉環響應，然后利用估計的閉環響應進行控制器參數整定，適用于不穩定系統并能夠利用瞬態輸入輸出數據.

1 磁浮列車懸浮控制系統建模與分析

本文以長沙磁浮列車為研究對象，每節列車的懸浮系統通過5個轉向架，20組電磁鐵給車體提供懸浮力.忽略空氣彈簧作用力的影響，懸浮系統通過轉向架機械解耦后可以簡化為單點懸浮系統，如圖1所示.磁浮列車單點懸浮系統簡化模型示意如圖2所示.

圖1 磁浮列車懸浮系統單轉向架機械解耦結構示意Fig.1 Schematic diagram of mechanical decoupling structure of single bogie of maglev train levitation system

圖2 磁浮列車單點懸浮系統模型示意Fig.2 Schematic diagram of single-point levitation system model of maglev train

考慮磁浮列車單點懸浮系統，經過在懸浮平衡點位置處線性化處理后的模型描述如下[13]：

根據長沙磁浮列車的數據可知： μ0=4π×10-7H/m，is=22.0A，zs=8.0 mm，N=360 匝，A=0.038 m2，R=0.92 Ω，m=535 kg.

實際磁浮列車懸浮系統調試過程中，常采用PID算法來設計懸浮系統控制器，針對懸浮系統電磁鐵對象部分的一階慣性滯后環節，可得

式中：Gi(s) 為電壓轉換電流環節的傳遞函數.

設計電流負反饋內環，如圖3中紅框部分，將懸浮系統降階為二階系統，懸浮系統的開環傳遞函數G(s)=Gi(s)Gz(s)，其中，Gz(s) 為電磁鐵部分的傳遞函數，如式（3）.再進行懸浮間隙反饋回路PID控制器的設計[14].

圖3 帶有電流負反饋內環的懸浮系統閉環反饋示意Fig.3 Closed loop feedback diagram of levitation system with negative current feedback inner loop

此時取狀態變量為 [Δz(t)Δz˙(t)]T，得到懸浮系統模型的狀態空間描述為

根據長沙磁浮列車的數據可以得到此懸浮系統狀態空間描述的系統矩陣，控制矩陣輸出矩陣C=[1 0].

由該狀態空間模型可知：懸浮系統存在位于右半平面的極點，磁浮列車懸浮系統是開環不穩定系統，需要設計閉環反饋控制器使該系統輸出間隙值能夠穩定控制在設定間隙位置處.并結合經驗和試驗整定得到最佳控制器參數，但是這個過程需要經過大量的試驗才能夠得到一組比較好的PID控制器參數.

2 基于數據驅動的控制器參數整定

在實際懸浮系統控制器調試過程中，雖然無法很快得到一組PID控制器參數使得懸浮控制器具有很好的性能，但是，根據調試經驗以及數次試驗，還是能夠較快地獲得一組能夠保證系統穩定的控制器參數.在懸浮系統穩定的情況下，本文提出一種基于懸浮系統單次調試的輸入輸出數據的控制器參數整定方法，該方法能夠不依賴懸浮系統對象的模型信息，設計完成具有優異性能的懸浮控制器.

本文提出的基于數據驅動的懸浮系統控制器參數整定方法不改變原有的控制器設計路線，保證了既有的懸浮系統控制器硬件配套控制板的兼容性，該方法是在原有系統基礎上對懸浮系統控制性能的優化設計.因此，該方法非常適合用來解決磁浮列車懸浮系統現場控制器調試問題.

針對磁浮列車懸浮系統，通常可以采用基于模型參考的控制器調整方法，設計一個期望控制性能的閉環參考模型，則懸浮系統控制器參數整定的目標是使參考模型和系統實際模型之間的差異盡可能的小[15].

懸浮系統閉環反饋系統如圖4所示，懸浮系統控制器參數整定目標可表述為最小化代價函數JM，如式（5）.圖中：P為被控對象的數學模型；C為控制器的數學模型；rt為懸浮系統的間隙設定值；u為控制器的輸出（即電壓）；e為系統的跟蹤誤差信號；d為測量噪聲.

圖4 懸浮系統閉環反饋系統示意Fig.4 Closed loop feedback system of levitation system

式中：M為參考模型的傳遞函數；W為加權函數，用于控制系統某些頻率范圍內的性能[16].

懸浮系統對象P的信息對于該代價函數的最小化至關重要.

由于無法獲取懸浮系統準確模型信息，而懸浮系統的輸入輸出數據可測量得到 并且能夠反映模型的信息.因此，本文根據懸浮系統單次懸浮調試的輸入輸出數據來整定控制器參數.該數據驅動的懸浮控制器參數整定方法完全跳過了系統建模過程，而是將懸浮控制器（解決模型匹配問題的控制器）識別過程表述為參數優化問題，具體是直接對懸浮控制器參數進行優化[17].

2.1 基于虛擬參考反饋的懸浮系統控制器參數整定

考慮閉環系統中的參數化的控制器C，如圖5所示，圖中：r? (t) 為虛擬參考信號； θ 為待整定的控制器參數矩陣.如果e和懸浮系統輸入信號u已知，則模型匹配問題可以重新表述為控制參數的識別問題[16].

圖5 基于懸浮系統輸入輸出數據的控制器參數整定原理示意Fig.5 Schematic diagram of controller parameter tuning based on input and output data of levitation system

虛擬參考信號r? (t) 滿足

則系統控制器的期望輸出u(t) 為

由于式（5）的分子和分母中都存在參數，使得最小化問題相對于 θ 是非凸的，這大大增加了它的難度.為了使問題具有可處理性，必須確定凸優化準則[16].

現在考慮代價函數Jv為

式中：L為合適的預濾波器描述；E[·]為期望；uL和eL分別為經濾波后的控制器輸出和系統跟蹤誤差，如式（9）、（10）.

通過選擇適當的預濾波器L，能夠使兩個代價函數（JM和JV）是等效的.根據文獻[4]可知

式中：p(u) 為控制器輸出數據u的功率譜密度.

考慮選用如下控制器：

式中： β 為控制器參數向量的系數矩陣.

因此，JV變為

參數整定算法1步驟：

步驟1根據閉環系統的輸入輸出數據對（u0（t），z0（t））和期望參考模型M計算虛擬參考信號以及相應的跟蹤誤差；

步驟2計算預濾波器并將其應用于u（t）和z（t）以獲得濾波信號uL(t) 和zL(t) ；

步驟3計算使代價函數最小化的最佳參數向量.

2.2 基于估計閉環響應數據驅動的控制器參數整定

上述懸浮系統控制器參數整定算法1需要選擇合適的參考模型，參考模型的選擇將影響到參數整定的結果.本節提出了一種改進的利用估計閉環響應數據驅動的控制器參數整定方法.所提出的方法通過引入虛擬信號來估計非最小相位系統或不穩定系統的閉環響應[18].

考慮輸入數據序列為

估計輸出間隙數據序列為

輸出間隙數據序列為

式中：G為系統脈沖響應；u中各項是相互線性無關的，即滿足u=Uα ， α 為系數矩陣，U為單次調試控制器輸出數據矩陣， α =[α0α1···αN-1]T, α ∈RN，U=[u0u1···uN-1],U∈ RN×N.

輸出間隙數據序列為z=Zα ，Z為單次調試懸浮系統輸出間隙數據矩陣，

對于數據長度為N的輸入輸出數據序列，可以通過N次獨立的實驗來獲取得到，不過這將花費大量的時間.為了使用單次懸浮調試實驗輸入輸出數據估計，定義控制器輸出數據向量和懸浮系統輸出間隙數據向量分別為uk和zk：uk=[01×ku0(0)u0(1) ···u0(N-1-k)]T，zk=[01×kz0(0)z0(1) ···z0(N-1-k)]T.其中：u0(0)≠0 ，每一個uk都是線相互性無關的；k=0，1，2， ··· ，N-1.

通過消去 α 可以得到

故可以得到G=ZU-1.因此，脈沖響應G是可以根據無噪聲情況下單次實驗的輸入輸出數據對(uone(t),zone(t))得到的.可以通過使用一次性實驗數據 (uone(t),zone(t)) 來估計系統任意輸入數據序列u的輸出數據序列z[18].然后使用虛擬參考信號來估計系統閉環響應.根據閉環系統的輸入輸出數據對(uone(t),zone(t))和r來估計系統閉環響應 (u(t),z(t)) ，引入，如式（21）.

因此，對任意最小相位控制器C，數據對zone(t))能夠用來描述系統的輸入輸出間關系，如式（22）.

閉環系統輸出數據序列可根據式（23）估計.

同理，閉環系統的輸入數據序列可類似估計為

式中：r=[r0r1···rN-1].

參數整定算法2步驟[19]：

步驟1根據閉環系統的輸入輸出數據對（uone（t），zone（t））和r來估計系統閉環響應；

步驟2計算相應的跟蹤誤差e；

步驟3計算使代價函數最小化的最佳參數向量.

2.3 基于信號投影的磁懸浮系統數據噪聲抑制

上一小節考慮的是在輸入輸出數據無噪聲情況下的磁懸浮系統參數整定方法，然而通常情況下，磁浮列車工作在復雜的環境中，輸入輸出數據不可避免地會受到噪聲的影響.

本節采用信號投影的方法實現磁懸浮系統輸入輸出數據噪聲的抑制.具體步驟是通過合理選擇低通濾波器來設計一組無噪聲數據基向量，然后將帶噪聲的數據投影到該組無噪聲數據基向量所表示的子空間中[19].定義無噪聲數據基向量為

式中：Mv為基向量的數量，需要合理選擇；T和F為經合理設計的低通濾波器的傳遞函數，其截止頻率根據輸出數據的頻譜分析以及系統的控制帶寬得到[20]；k=0,···,N-1,i=1,2,···,Mv.

帶噪聲的數據和投影基向量為

式中：zk0為單次采樣的帶噪聲的間隙數據.

由投影基向量構成的無噪聲數據為

式中：zkp為單次采樣的去噪聲的間隙數據.

結合式（21），可得到改進的r? (t) 為

3 懸浮系統仿真與實驗分析

PID控制算法在商業運營的長沙和北京中低速磁浮列車中已經得到了很好的應用，以磁浮列車單點懸浮系統為研究對象，為保證懸浮系統穩定工作在穩定時間間隙z0處，本節采用PID控制算法來實現懸浮系統控制器的設計.設計得到單點懸浮系統控制律為

式中：kp= －7 000，為比例系數；kd= －100，為微分系數；ki= －5 000 為積分系數.

得到參數整定前基于PID控制的單點懸浮系統閉環響應仿真曲線，如圖6所示.

圖6 單點懸浮系統輸入數據曲線Fig.6 Input data curve of single-point suspension system

則基于數據驅動的懸浮控制器參數整定后的單點懸浮系統閉環響應仿真曲線如圖7所示.

圖7 懸浮控制器參數整定后單點懸浮系統閉環響應仿真曲線Fig.7 Simulation curves of closed-loop response of single-point levitation system before and after levitation controller parameter tuning

由圖7可知：此時的單點懸浮系統經過PID控制器的閉環反饋控制以后雖然能夠達到穩定，但是系統的懸浮控制性能并不好.

在此基礎上，為了進一步整定控制器參數，首先收集單點懸浮系統的單次懸浮實驗的輸入輸出數據，然后采用本文所提出的基于數據驅動的控制器參數整定方法，整定得到單點懸浮系統的控制律為

同時，結合該單點懸浮系統的單次懸浮實驗的輸入輸出數據，分析研究采用基于虛擬參考反饋的懸浮系統控制器參數整定方法的整定效果，根據單點懸浮系統仿真實驗，得到如圖8的考慮不同參考模型的虛擬參考反饋懸浮控制器參數整定后的單點懸浮系統閉環響應仿真曲線.

由圖8可知：基于虛擬參考反饋的懸浮系統控制器參數整定方法的整定效果比較依賴于參考模型的選取，而本文所提出的基于數據驅動的懸浮系統控制器參數整定方法則不依賴于參考模型.

圖8 單點懸浮系統閉環響應仿真曲線Fig.8 Simulation curves of closed-loop response of single point levitation system

此外，根據圖7、8的仿真結果，計算得到懸浮控制器參數整定前、后系統輸出的懸浮間隙數據的積分平方誤差（ISE）和積分絕對誤差（IAE）， 如表1所示.

根據表1和圖7、8可知：經過控制器參數整定后，懸浮系統的懸浮控制性能提升，仿真實驗結果驗證了本文所提出方法的有效性.

表1 懸浮控制性能指標Tab.1 Levitation control performance indexes

為了進一步進行現場實驗驗證，本文在單鐵磁懸浮系統懸浮控制實驗平臺上進行了單點懸浮實驗，如圖9所示.該單鐵磁懸浮系統等效質量m=6.9 kg，穩定懸浮時zs=4.0 mm，is=9.5 A，A=13.5 cm2，N=300 匝，R=4.8 Ω.

圖9 單鐵磁懸浮系統懸浮控制實驗裝置Fig.9 Experimental device for levitation control of single-iron magnetic levitation system

完全結合磁浮列車懸浮系統的現場調試工作流程，通過反復調節懸浮控制板PID控制器參數來進行懸浮實驗.所不同的是，結合本文基于數據驅動的控制器參數調整方法，現場調試人員無需經過漫長的PID參數調試，直到懸浮系統達到優異控制性能時才結束，調試人員只需將懸浮系統調試到穩定懸浮即可.

結合本文所提出的基于數據驅動的磁浮列車懸浮系統控制器參數整定方法，當懸浮系統調試穩定時（如圖10所示）， 收集此刻單次調試的懸浮系統輸入輸出數據序列，用于后續控制器參數整定.

由圖10可知：測量得到的懸浮系統間隙輸出數據是帶有噪聲的.因此，首先采用上節提出的基于信號投影的磁懸浮系統數據噪聲抑制方法來實現對系統輸出數據的噪聲抑制.設計用于信號投影的低通濾波器T和F分別為

圖10 基于PID的單點懸浮系統閉環反饋控制響應實驗曲線Fig.10 Experimental response curves of closed loop feedback control of single-point levitation system based on PID

再根據式（29）可以得到經噪聲抑制處理后的單點懸浮系統間隙輸出數據，如圖11所示.經噪聲抑制處理前、后的帶噪聲的懸浮間隙數據的方差分別為 4.90×10-4和 2.25×10-4，噪聲水平下降了 54.1%.

圖11 經噪聲抑制處理后的單點懸浮系統閉環反饋控制響應實驗曲線Fig.11 Experimental response curves of closed-loop feedback control of single-point levitation system after noise suppression

根據經噪聲抑制處理后的單點懸浮系統閉環反饋控制響應間隙輸出數據，采用算法2可以計算得到整定后的控制律為

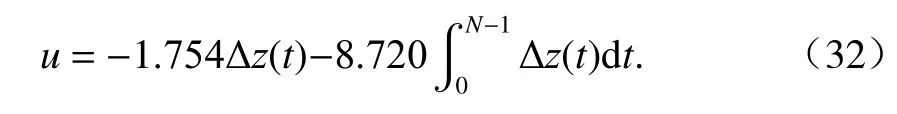
最后，在單鐵磁懸浮系統懸浮控制實驗平臺上采用該控制器進行懸浮實驗，得到懸浮控制器參數整定前、后的單點懸浮系統閉環響應實驗曲線，如圖12所示.系統階躍響應的超調量由參數整定前的0.50 mm降低到參數整定后的0.14 mm，降低72.0%.懸浮控制器參數整定前、后單點懸浮系統閉環響應實驗的懸浮控制性能指標如表2所示.

由表2和圖12可知：控制器參數經快速整定好后的懸浮系統，相對于初始條件下僅僅只是粗調好的PID反饋控制系統，其階躍響應具有更小的超調以及更高的控制精度，參數整定后的ISE下降79.8%，IAE下降54.5%，說明本文所提出的基于數據驅動的磁浮列車懸浮系統參數整定方法能夠滿足工程實際中對于磁浮列車控制器參數的快速整定的需求，并且具有較好的控制性能.現場實驗結果驗證了本文所提出的磁浮列車懸浮系統參數整定方法的有效性.

圖12 懸浮控制器參數整定前、后單點懸浮系統閉環響應實驗曲線Fig.12 Experimental curves of closed-loop response of single-point levitation system before and after parameter tuning of levitation controller

表2 參數整定前、后單點懸浮系統的懸浮控制性能指標Tab.2 Levitation control performance indexes of single-point levitation system before and after parameter tuning

4 結 論

本文針對懸浮系統的開環不穩定性和復雜非線性會給控制器參數整定帶來較大困難的問題，提出了一種基于數據驅動的磁浮列車懸浮系統控制器參數快速整定方法，無需懸浮系統的精確模型，只根據單次懸浮調試實驗的輸入輸出數據.并且針對數據噪聲的問題，應用基于信號投影的噪聲抑制方法，將帶噪聲數據的方差降低了54.1%.最后通過單鐵懸浮實驗，驗證了基于數據驅動的參數整定方法能夠快速地整定好懸浮系統控制器參數，經參數整定后的系統相對于初始條件下只粗調好的PID反饋控制系統的階躍響應超調量下降72.0%，ISE下降79.8%，IAE下降54.5%.