永磁電磁混合Halbach陣列電動懸浮的穩定性控制

羅 成 ，張昆侖 ，王 瀅

（1.西南交通大學電氣工程學院，四川 成都 611756；2.西南交通大學磁浮技術與磁浮列車教育部重點實驗室，四川 成都 611756）

永磁電動懸浮原理為利用永磁體與非磁性導體之間的相對運動在導體中感生渦流，該渦流與空間磁場相互作用產生所需的懸浮力.該系統結構簡單，能實現自穩.但永磁電動懸浮由于自身的欠阻尼特性，使得系統在受到外界擾動時易產生振動，且較長時間內不能穩定，嚴重情況下甚至發生安全事故[1-3].

對于永磁電動懸浮穩定性的研究，國內外學者主要通過增加系統無源阻尼或有源阻尼的方式提高系統懸浮穩定性.鄭杰通過解析法證明了在線圈式永磁電動懸浮系統中添加無源阻尼線圈可增加系統阻尼，但線圈軌道的等效電路計算模型不適用于電感難以計算的導體板軌道[4].文獻[5-6]通過實驗平臺直接測量了添加無源阻尼板后的永磁電動懸浮系統電磁阻尼值，并根據測量數據對系統阻尼進行了分析.文獻[7-8]提出將電磁鐵Halbach陣列與永磁體Halbach陣列同時并行安裝于車體，通過電磁鐵對EDS （electrodynamic suspension）系統懸浮力進行調節，實現系統阻尼主動控制.但電磁鐵與永磁體之間存在磁場耦合，空間磁場難以準確計算.Han等[9]提出了一種電磁永磁間隔排列構成的混合磁陣列，其通過電磁鐵可對空間磁場及電磁力進行主動控制，但存在線圈安匝數過大且較難得到精確的解析計算結果.文獻[10-12]研究了一種電磁EMS （electromagnetic suspension）和永磁EDS混合磁懸浮系統.其通過永磁EDS提供懸浮力的同時，利用電磁EMS對懸浮力進行動態調節，達到系統阻尼主動控制的效果，但該混合磁浮系統的結構及電磁EMS的控制系統都較為復雜.

基于以上研究，本文對一種永磁電磁混合Halbach陣列電動懸浮系統的穩定性控制進行了研究.首先利用電磁場理論推導出系統懸浮力2D解析式，并對其進行了有限元驗證；其次設計了基于氣隙反饋的PID控制器；最后基于所設計的控制器，仿真分析了系統在受到外界擾動時的動態懸浮性能，證明了所設計的懸浮控制器可使系統快速實現動態穩定.

1 懸浮力計算

本文所研究的永磁電磁混合Halbach陣列電動懸浮示意見圖1.圖中：lm為永磁體長度；h為永磁體高度； δ 為線圈所占寬度；w1及w2分別為永磁體和導體板橫向寬度；l1及l2分別為陣列和非磁性導體板長度；τ為極距；v為相對速度.為方便陣列模塊制造，設h=lm+ 2δ.

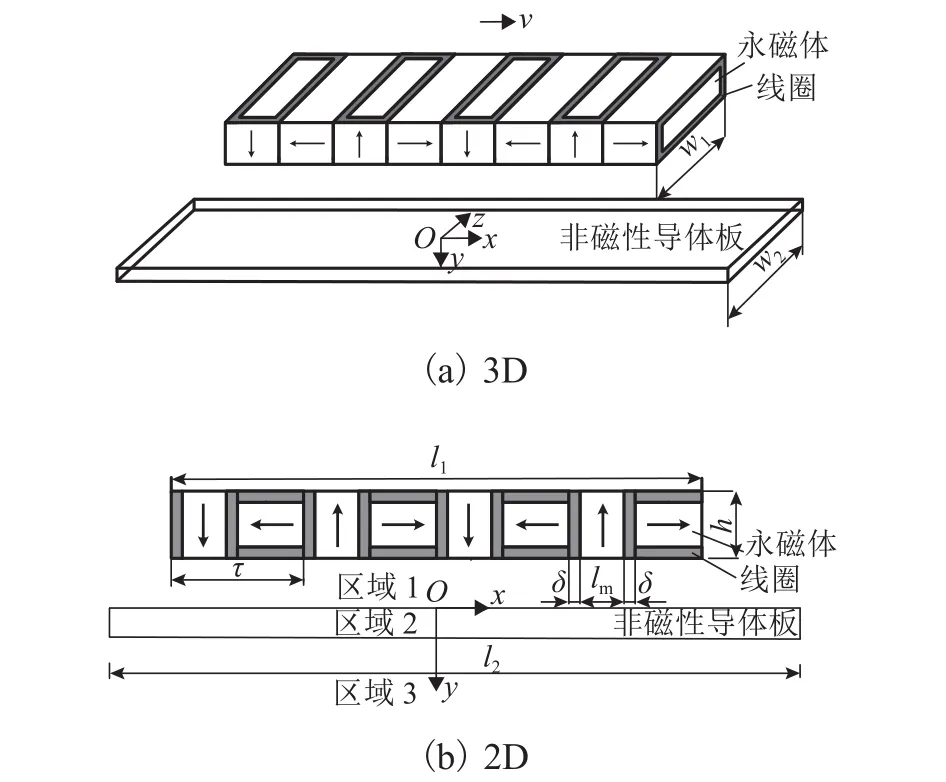
圖1 永磁電磁混合Halbach陣列電動懸浮示意Fig.1 Diagram of PM and electromagnet hybrid Halbach array EDS system

1.1 解析計算

如圖1所示，由于永磁電磁混合Halbach陣列產生的源磁場含有端部效應和氣隙諧波的影響，故需對其進行傅里葉分解，如式（1）.

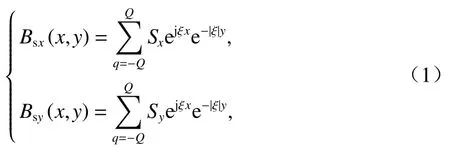
式中：Bsx(x,y)、Bsy(x,y)分別為永磁電磁混合Halbach陣列源磁場傅里葉分解后的x、y分量磁場；Q為諧波次數；ξ=2πq/l2；Sx、Sy為傅里葉系數，如式（2）.

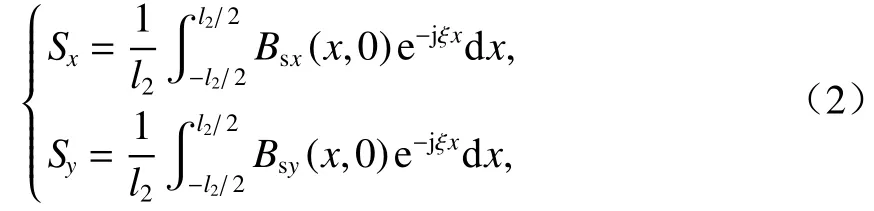
式中：Bsx（x,0）、Bsy（x,0）分別為永磁電磁混合 Halbach陣列在非磁性導體板上表面產生的x、y分量源磁場，由混合陣列永磁體及表面線圈在外部空間產生的磁場進行疊加所得，具體解析表達式可參考文獻[13-14].

當車載混合Halbach陣列以相對速度v運動切割非磁性導體板時，在導體板中感生渦流大小[15]為

式中：γ2為非磁性導體板電導率.

利用麥克斯韋方程組及洛倫茲規范，可推導出系統矢量磁位A的方程[16]為

式中：μ0為真空磁導率；Js為感生渦流矢量； ?2為拉普拉斯算子；ki為傳播函數[16]，且滿足式（5）條件.

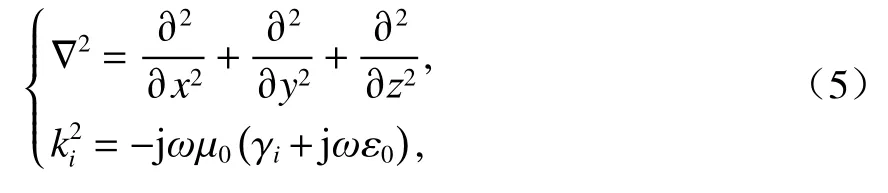
式中：ω為角頻率（ω=-ξv）；γi為氣隙電導率（i=1,3）；ε0為真空介電常數.

由于二維解析模型中，矢量磁位A和Js僅含有z方向分量.因此，根據式（4），可得到各區域矢量磁位標量為

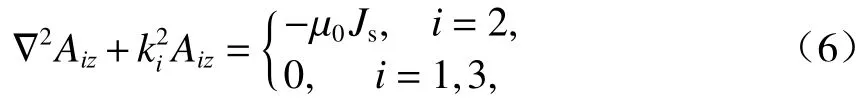
式中：Aiz為各區域矢量磁位z方向分量.

利用分離變量法求得式（6）的通解后，根據文獻[14-15]所得磁場邊界條件求得各區域矢量磁位.然后由B=▽ ×A可得各區域感生磁場為（i= 1, 2, 3）

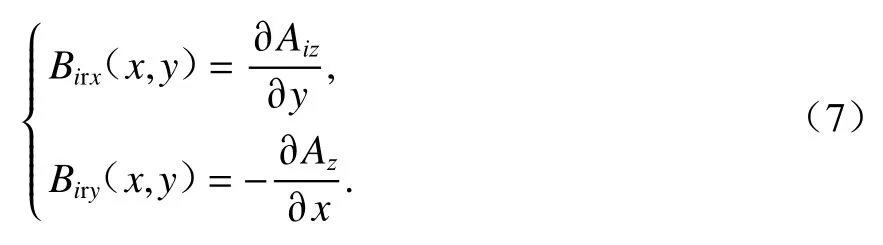
將源磁場與感生磁場求和，可得空間各區域磁場為（i= 1, 2, 3）

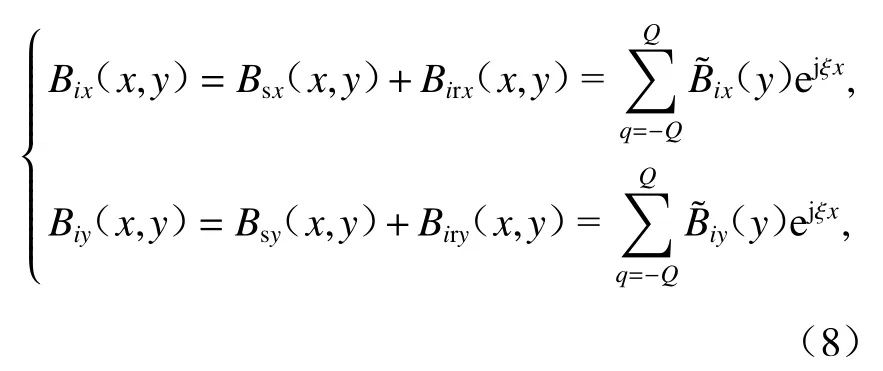
根據麥克斯韋張量法，可求得懸浮力[17-19]為

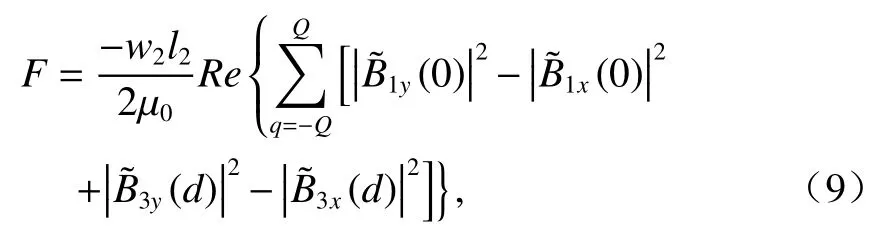
1.2 有限元數值計算

本文采用Ansys Maxwell有限元軟件搭建數值計算模型，對推導的永磁電磁混合Halbach陣列電動懸浮系統懸浮力2D解析表達式進行驗證，系統參數如表1所示.得到的有限元模型如圖2所示.

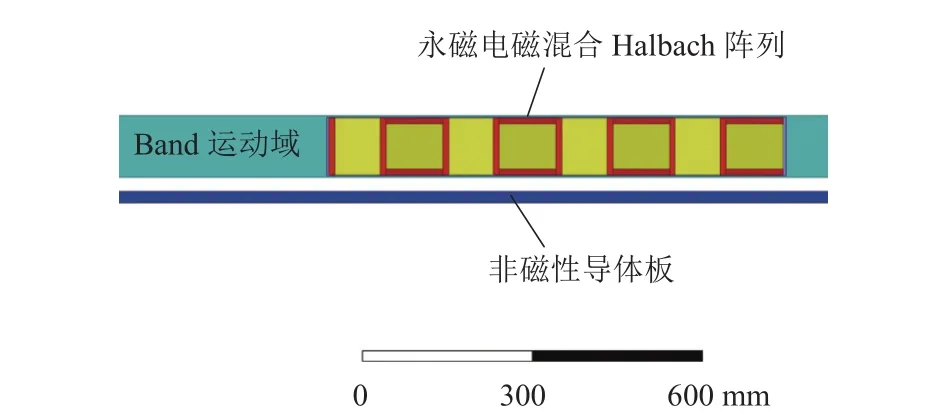
圖2 2D有限元模型Fig.2 2D FEM

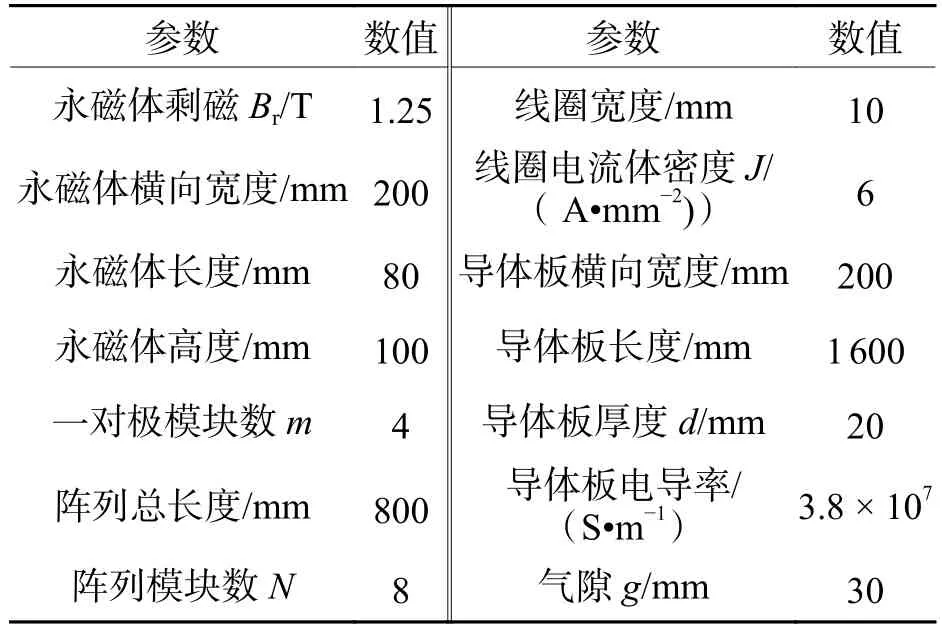
表1 模型參數Tab.1 Model parameters

不同運行速度下，懸浮力解析計算與有限元數值計算結果對比如圖3所示.從圖中可以看出，懸浮力解析解與有限元數值解吻合良好，驗證了懸浮力解析表達式的準確性.

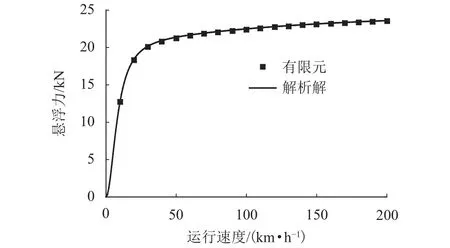
圖3 懸浮力隨運行速度的變化曲線Fig.3 Variation curve of suspension force with running speed

2 懸浮控制器的設計

2.1 數學模型的建立

當永磁電磁混合Halbach陣列電動懸浮系統穩定運行于平衡點（初始額定電流J0=0，初始額定氣隙g0=30 mm，其他參數見表1）時，懸浮力等于車體重量，即

式中：F0為平衡點處懸浮力；G為車體重量.

當系統受到外界擾動力作用時，以垂直向上為參考正方向，可得系統垂向動力學方程為

式中：Fd為外界擾動力.

由于式（11）為氣隙和電流的非線性方程，故需對式（11）在平衡點（g0,J0）處進行線性化處理.

對式（9）懸浮力在平衡點處泰勒級數展開，忽略高階項，得

式中：Δg為氣隙變化量；ΔJ為電流變化量；kg、kJ如式（13）.

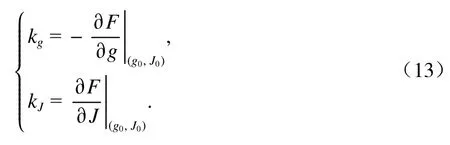
將式（10）和式（12）代入式（11），且結合 Δg=gg0，可得到系統近似線性化數學模型[20-22]，如式（14）.

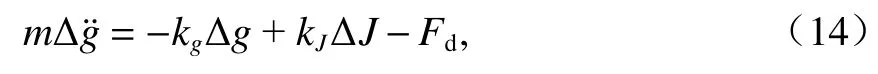
式中：kg、kJ及車體質量m可根據J0=0，g0=30 mm及表1參數求得.

2.2 定氣隙PID控制器

氣隙反饋懸浮控制器的反饋輸入量僅為懸浮氣隙，可通過氣隙傳感器實時監測得到.設ΔJ=其中：kP、kI、kD分別為比例、積分、微分控制參數.結合式（14），選擇狀態變量為可得系統閉環狀態方程為

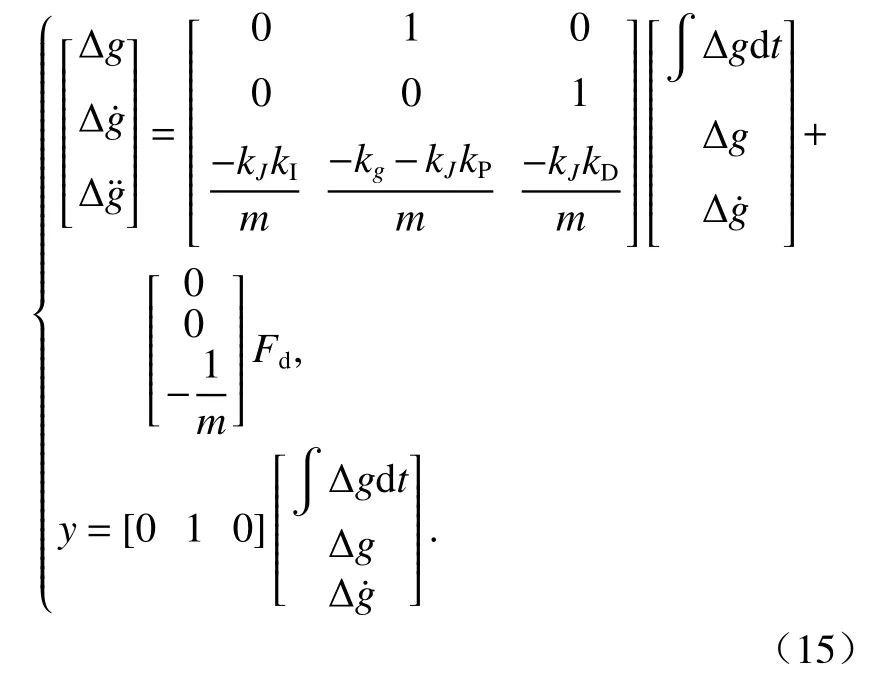
由系統閉環狀態方程可得其特征方程為

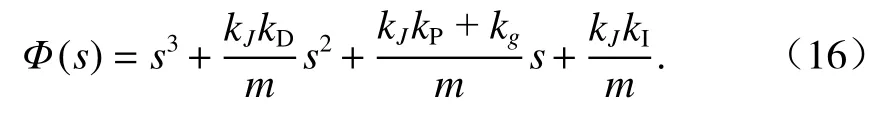
利用極點配置法，規定超調量不超過0.05，調整時間不超過0.1 s，可以求得期望特征方程為[2,22]

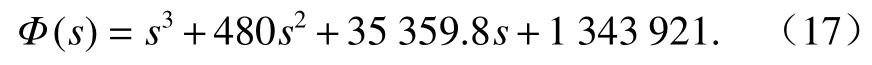
對比式（16）和式（17），可以求得kP=1.587 5 ×1011，kI=6.086 8 × 1012，kD=2.174 × 109.

設計的定氣隙PID控制仿真如圖4所示.

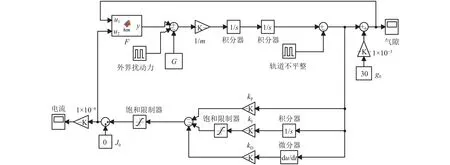
圖4 定氣隙PID控制仿真框圖Fig.4 Simulation block diagram of fixed air gap PID control

2.3 變氣隙PID控制器

定氣隙PID控制器可使系統在受到外界擾動時穩定運行于額定氣隙位置，但同時電磁鐵線圈需通入一定電流來抵消外界擾動.因此，該方法對于散熱較困難的永磁電磁混合Halbach陣列電動懸浮系統存在局限性.對于懸浮氣隙較大的電動懸浮系統，可考慮通過改變懸浮氣隙大小來抵消外界擾動，使得穩態狀態下的電流為0.因此，本文在定氣隙PID控制器的基礎上，設計了變氣隙PID控制器.

設計的變氣隙PID控制仿真如圖5.根據外界擾動力的變化在仿真模型中加入一函數模塊，用以計算出跟隨外界擾動力變化的初始氣隙變化量Δg0，用g0加上Δg0后作為新的額定氣隙，將其輸入PID函數模塊重新計算出相應的PID控制參數.

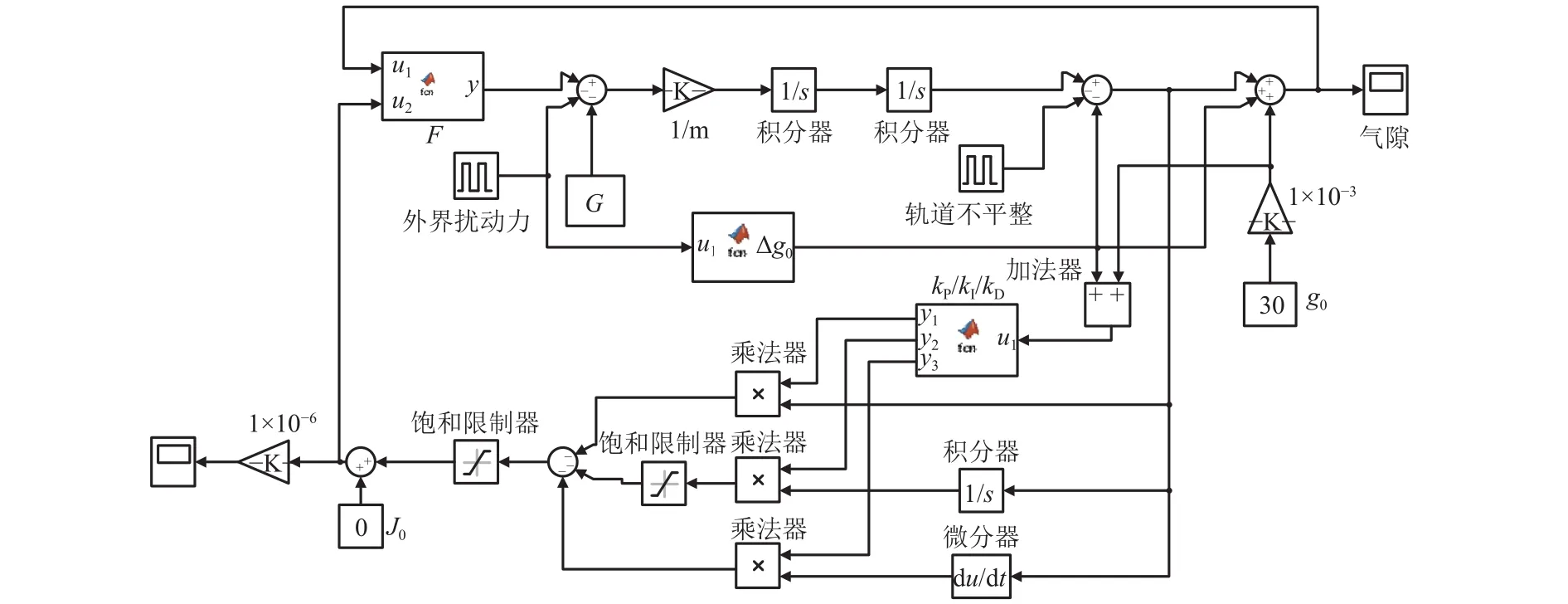
圖5 變氣隙PID控制仿真框圖Fig.5 Simulation block diagram of variable air gap PID control

3 仿真分析

當系統運行速度為200 km/h時，對以下3種工況分別進行仿真分析：1）系統受到外界1 000 N擾動力干擾，作用時間為 0.3～0.7 s；2）系統受到外界 -1 000 N擾動力干擾，作用時間為0.3～0.7 s；3）系統受到軌道1 mm沉降干擾，作用時間為0.3～0.7 s.

3.1 定氣隙PID控制

通過設計的定氣隙PID控制器，得到系統懸浮氣隙及線圈電流密度仿真波形如圖6所示.由圖可見：當系統受到 ±1 000 N外界擾動力作用時，系統能夠迅速穩定運行于30 mm額定氣隙，且穩定線圈電流分別為2.12 A/mm2和-2.17 A/mm2；當系統受到軌道1 mm沉降干擾時，系統也會迅速穩定于額定氣隙30 mm處，且穩定線圈電流為0.

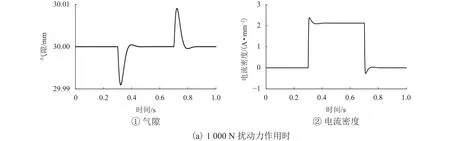
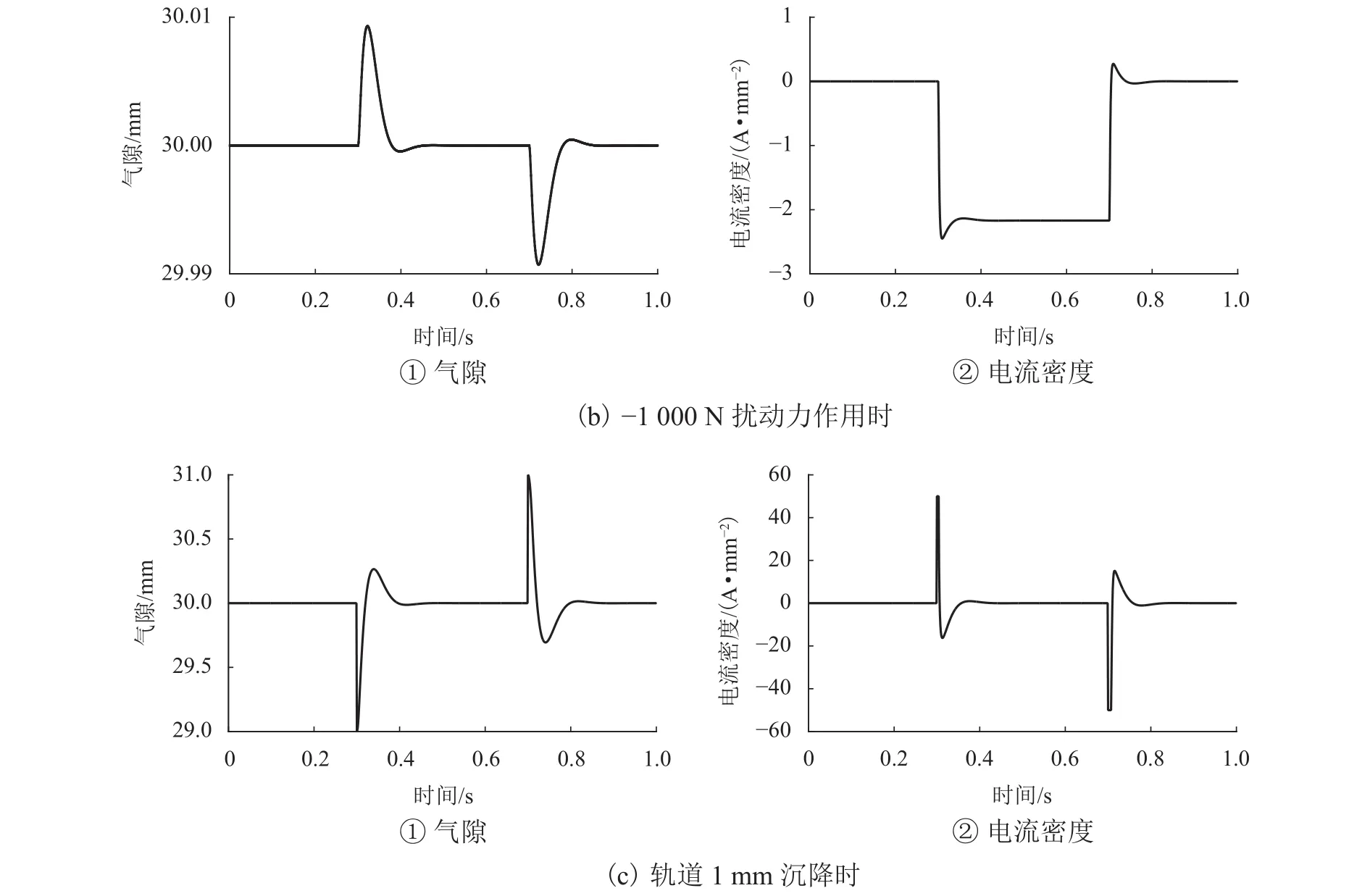
圖6 懸浮氣隙及線圈電流密度Fig.6 Suspension air gap and coil current density

3.2 變氣隙控制

通過設計的變氣隙PID控制器得到系統懸浮氣隙及線圈電流密度仿真波形如圖7所示.由圖可見：在系統受到軌道1 mm沉降干擾時，系統響應與定氣隙PID控制一致，能迅速穩定于額定氣隙30 mm，且穩態線圈電流仍為0； 當系統受到±1 000 N外界擾動力作用時，穩態狀態下，系統線圈電流為0，此時系統懸浮于28.5 mm及31.6 mm位置.相比于通過線圈電流來抵消外界擾動力的定氣隙PID控制，變氣隙PID控制則是通過改變懸浮氣隙以產生能夠與外界擾動力和車體重量平衡的懸浮力，大大減小了能耗與發熱.尤其對于永磁電磁混合Halbach陣列電動懸浮系統，存在散熱較困難的問題，變氣隙PID控制顯得更為適用.

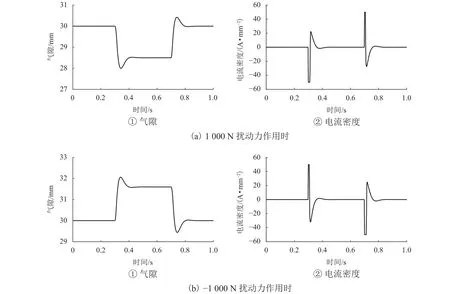
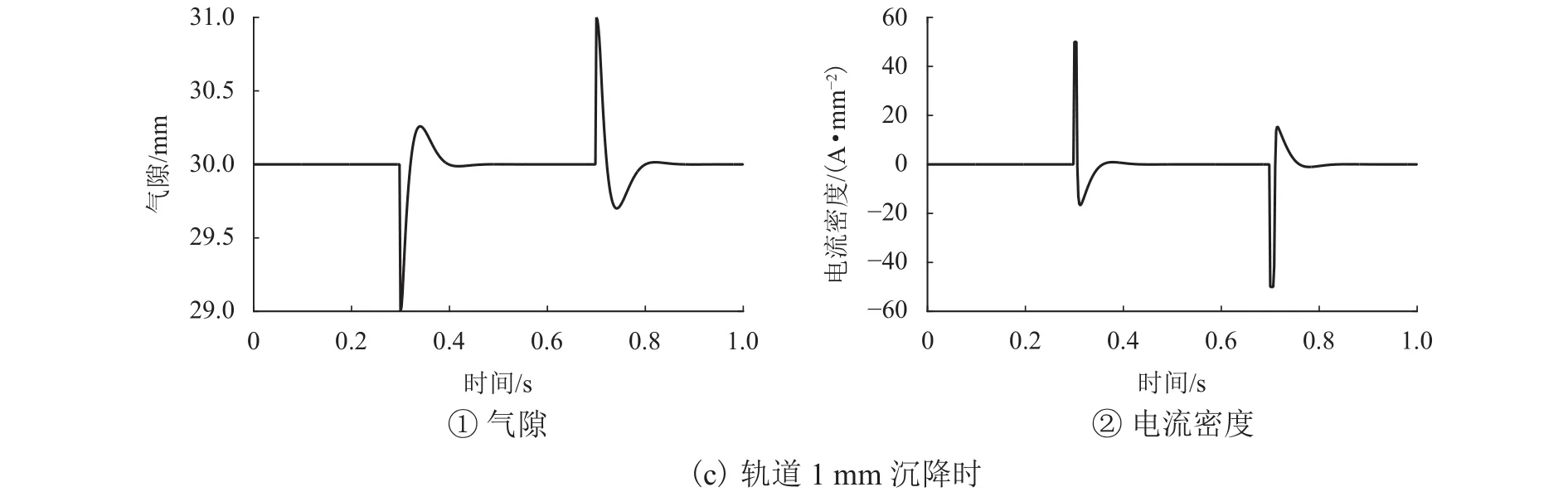
圖7 懸浮氣隙及線圈電流密度(變氣隙)Fig.7 Suspension air gap and coil current density (variable air gap )

4 結 論

本文基于永磁電磁混合Halbach陣列電動懸浮2D懸浮力解析式，設計了兩種PID懸浮控制器，并對其進行動態仿真，得到以下結論：

1） 通過設計的兩種PID控制器，系統在受到外界擾動時，均能實現動態快速穩定，可解決永磁電動懸浮因欠阻尼特性導致懸浮穩定性差的問題.

2） 當系統在受到 ±1 000 N外界擾動力作用時，定氣隙PID控制可使系統穩定于額定氣隙30 mm位置，但線圈需分別通入2.12 A/mm2和 -2.17 A/mm2穩態電流以抵消外界擾動力的影響.而變氣隙PID控制則使系統分別穩定懸浮于28.5 mm及31.6 mm位置，且穩態線圈電流為0.

3） 相比于定氣隙PID控制，變氣隙PID控制可有效降低線圈能耗和發熱，更適用于發熱較困難的永磁電磁混合Halbach陣列電動懸浮系統.