考慮電流振鈴特性的懸浮電磁鐵等效電路模型

梁 達 ，張昆侖 ，肖 嵩

（1.西南交通大學磁浮技術與磁浮列車教育部重點實驗室，四川 成都 611756；2.西南交通大學電氣工程學院，四川 成都 611756）

磁懸浮列車具有低噪、環(huán)保、緊湊和輕量化等優(yōu)點，是一種可以滿足人類對出行安全性、可靠性和快速性要求的新型載運系統.根據懸浮方式的不同，磁浮列車主要分為電磁懸浮和電動懸浮.電磁懸浮可以實現靜態(tài)懸浮，是目前商業(yè)運營磁浮線中廣泛采用的技術方案[1].電磁懸浮系統主要由懸浮電磁鐵、懸浮斬波器和懸浮控制器組成[2].

懸浮電磁鐵電流在懸浮斬波器的開關動作時刻伴隨著嚴重的振鈴現象.電流振鈴的頻率遠高于開關頻率，它會為電磁懸浮系統造成以下危害：

1） 增加懸浮電磁鐵和開關器件的電壓應力.因為高頻電流振鈴經過懸浮斬波器流入懸浮電磁鐵，快速變化的電流在功率環(huán)路（不包含懸浮電磁鐵）的等效電感（器件封裝寄生電感，引腳寄生電感以及印制電路板走線寄生電感）上感應出較大電壓振鈴[3].由于直流側供電電壓恒定，最終導致懸浮電磁鐵端電壓和開關器件電壓發(fā)生振鈴.從而增大懸浮電磁鐵和開關器件的電壓應力，加速懸浮電磁鐵和開關器件老化進程.2） 增大開關損耗.因為當快速變化的電流通過MOSFET的共源極寄生電感時，其負反饋作用會導致開關管導通時間和關斷時間延長[4]，從而增加開通損耗和關斷損耗.3） 造成電磁干擾（electromagnetic interference，EMI）.因為電流振鈴頻率遠高于開關頻率，開關暫態(tài)過程中的較大的電壓變化率和電流變化率都是EMI干擾的根本來源[5].在電磁懸浮系統中，懸浮控制器、輔助電源以及網絡傳輸模塊均與懸浮斬波器集成在懸浮控制箱中，因此，電流振鈴引起的遠場干擾可能影響這些電子電路的正常工作，從而使懸浮控制箱難以通過電磁兼容測評.4） 影響懸浮控制效果.因為高頻電流振鈴會被懸浮電磁鐵的等效電容旁路，對懸浮系統的主磁通和電磁力沒有貢獻，然而該振鈴信號會被懸浮控制器的采樣系統收集，直接參與懸浮控制算法[6]，從而影響懸浮控制器輸出.因此，為了能夠提出有效的懸浮電磁鐵電流振鈴抑制措施，首要任務是研究其產生機理.

目前，對電磁懸浮系統的研究主要集中在對不同懸浮控制算法[7]、懸浮斬波器拓撲[8]以及懸浮電磁鐵結構優(yōu)化[9]等方面，沒有相關文獻對懸浮電磁鐵電流振鈴現象進行專門研究.在電力電子變換器領域，普遍認為開關振鈴現象是由于功率回路中的寄生電感和寄生電容形成LC振蕩腔，在開關動作時刻所產生的較大電壓變化率和電流變化率激勵作用下，電感中儲存的磁場能量和電容中儲存的電場能量發(fā)生交換而形成的[10].許多學者已經從開關器件模型的角度出發(fā)，對開關支路的振鈴進行了深入研究，但研究過程中將感性負載理想化為恒流源，即認為開關瞬間感性負載電流恒定[11]，顯然，這種假設在電磁懸浮系統中并不合理.因此，上述研究中得到的結論不完全適用于電磁懸浮系統.本文從懸浮電磁鐵等效電路的角度出發(fā)，研究其電流振鈴的產生機理.

1 懸浮電磁鐵的LRC阻抗網絡

圖1給出了中低速磁浮列車電磁懸浮系統的實現原理及懸浮斬波器和懸浮電磁鐵結構.

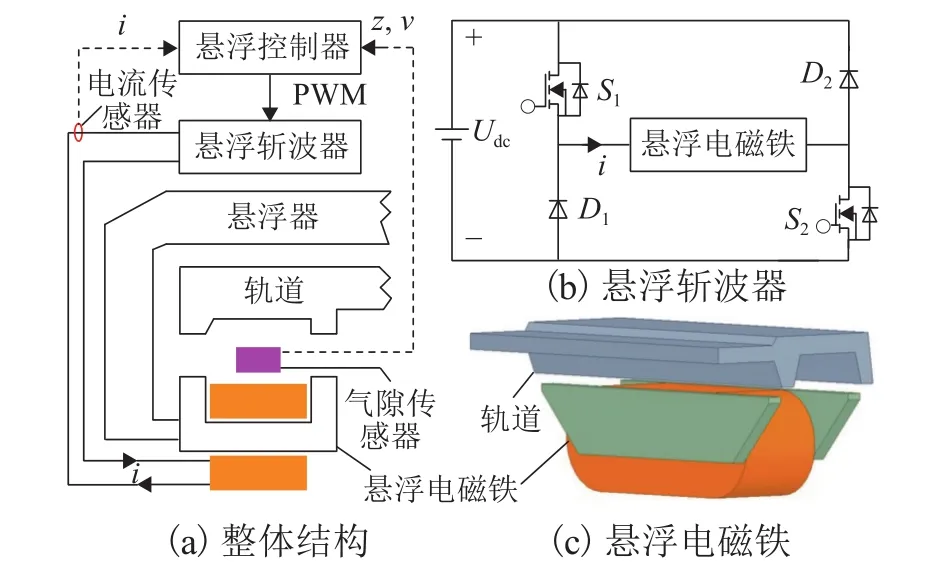
圖1 中低速磁浮列車電磁懸浮系統組成Fig.1 Composition of the electromagnetic suspension system in medium-low speed maglev trains

圖1（a）中：i表示懸浮電磁鐵電流，z、v表示懸浮氣隙和氣隙加速度.在該電磁懸浮系統中，懸浮電磁鐵安裝在軌道下方，懸浮控制器收集i、z和v信號，并通過特定的算法對上述信號進行處理，輸出脈寬調制（pulse width modulated，PWM）信號驅動懸浮斬波器工作，最終實現對懸浮力的調節(jié).圖1（b）中：Udc表示懸浮斬波器的供電電壓，S1、S2為全控型開關器件（如 IGBT、MOSFET或 SiC等），D1、D2為續(xù)流二極管.為了實現最快電流響應速度，懸浮斬波器采用S1和S2同時通斷的工作模式.圖1（c）中：懸浮電磁鐵的鐵芯為實心導體，繞組為矩形截面鋁線，U型懸浮電磁鐵和F型軌道配合可實現自導向.

將懸浮電磁鐵的每匝繞組視為一個獨立的導體單元，則任意兩匝繞組間存在寄生電容效應.但考慮到相鄰繞組間（同層相鄰繞組間和非同層相鄰繞組間）的寄生電容遠大于對角相鄰繞組間和非相鄰繞組間的互感和電容效應，在忽略后者的條件下，懸浮電磁鐵可以被抽象為圖2所示的單端口LRC無源阻抗網絡.其中，紅色虛線框部分表示電磁鐵繞組，tnm（n=1，2，···，N；m=1，2，···，M） 為懸浮電磁鐵第n層的第m匝繞組，N為電磁鐵繞組層數，M為電磁鐵每層繞組匝數.Uc(s)和I(s)分別為懸浮電磁鐵電壓和電流的象函數，s為象函數的自變量.Z(s)和Y(s)分別為懸浮電磁鐵的策動點阻抗和策動點導納.懸浮電磁鐵任意兩匝繞組之間通過電感、電阻、電容或其組合電路連通.假設懸浮電磁鐵LRC阻抗網絡的內部支路數為B，Ub(s)和Ib(s)（b=1，2，···，B）分別為第b支路電壓和電流的象函數，Lb、Rb和Cb分別為第b支路的電感、電阻和電容.

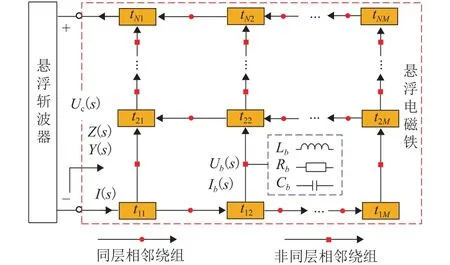
圖2 懸浮電磁鐵的LRC阻抗網絡Fig.2 LRC impedance network of a suspension electromagnet

1.1 策動點函數分析

圖2中，Z(s)可表示為

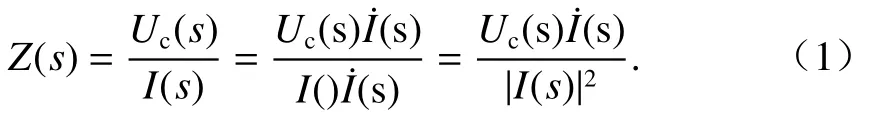
這里規(guī)定Uc(s)與I(s)方向相反，Ub(s)與Ib(s)方向相同.則由特勒根定理或復功率平衡得

將式（2）代入式（1）得懸浮電磁鐵的策動點阻抗為

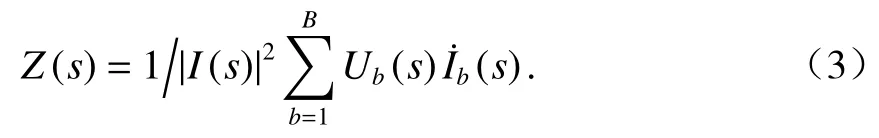
由歐姆定律得第b支路的電壓為

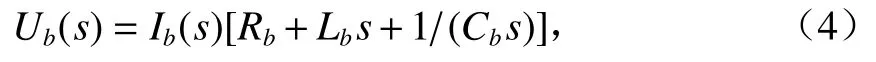
將式（4）代入式（3），則Z(s)可表示為

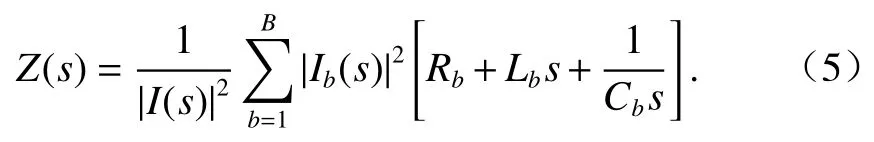
定義式（6）所示的能量函數：

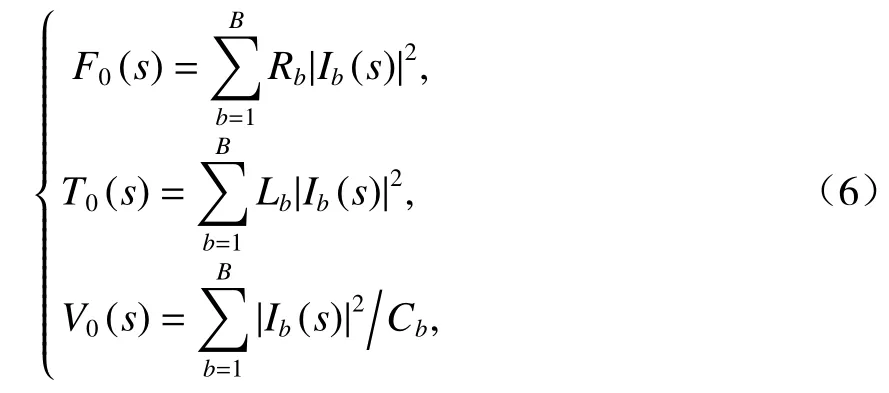
式中：F0(s)、T0(s)和V0(s)分別為與LRC網絡中電阻、電感和電容相關的能量函數.

在正弦穩(wěn)態(tài)條件下，即當s=jω時（ω為角頻率），式（6）中F0(s)、T0(s)和V0(s)可以表示為

式中：P、Wm和We分別為懸浮電磁鐵LRC阻抗網絡的有功功率、平均磁場儲能和平均電場儲能.

對于無源LRC網絡，在整個復平面上能量函數不小于0，即

Z(s)和Y(s)可分別用能量函數表示為

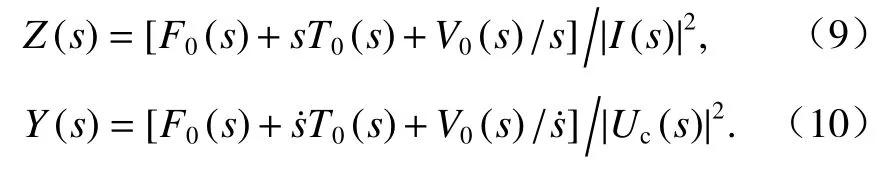
Z(s)和Y(s)統稱為懸浮電磁鐵的導抗函數，后文用G(s)統一表示.

1.2 導抗函數零極點分布規(guī)律

將s=σ 代入式（9），得

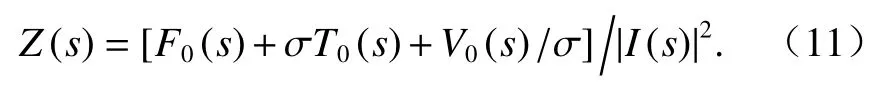
將s=σ+jω代入式（9），兩端取實部得

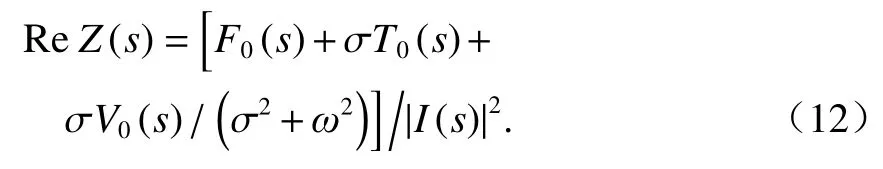
由式（11）可知，當自變量s為實數時，Z(s)也為實數，即s面的實軸變換為Z(s)面的實軸.由式（12）可知，當 Res=σ≥ 0 時，ReZ(s) ≥ 0，即s的右半閉面變換到Z(s)的右半閉面.因此，根據復變函數知識可知Z(s)為正實函數，具有以下性質[12]：1）Z(s) 的右半平面是解析的，即Z(s)的極點不可能落在右半平面；2）Z(s)在右半平面不存在零點；3）Z(s)在虛軸上若有極點或零點，只能是一階；4） 設Z(s) =N(s)/D(s)，N(s)和D(s)分別為Z(s)的分子多項式和分母多項式，則N(s)和D(s)的最高次冪之差和最低次冪之差均不超過1；5）Z(s)在虛軸上的實部為非負數，即 R eZ(jω)≥ 0.則Z(s)的一般形式為

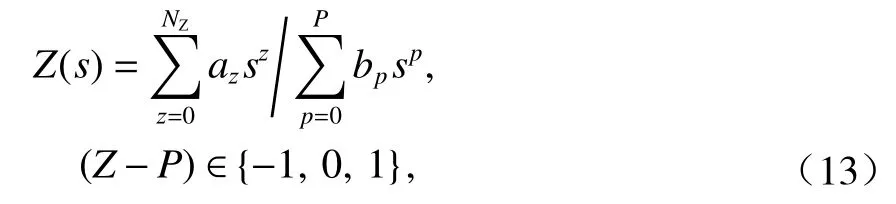
式中：az和bp分別為分子多項式和分母多項式的系數，均為正實常數；NZ為分子多項式的最高次數；P為分母多項式的最高次數.

根據式（9）可知，Z(s)的零點滿足

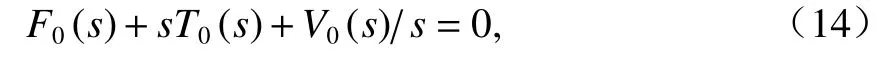
因此，Z(s)的零點可以表示為

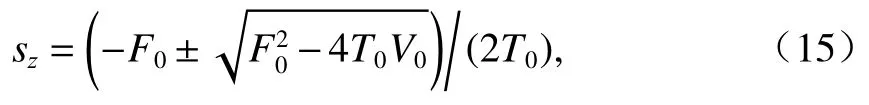
式中：T0、F0和V0即T0(s)、F0(s)和V0(s).

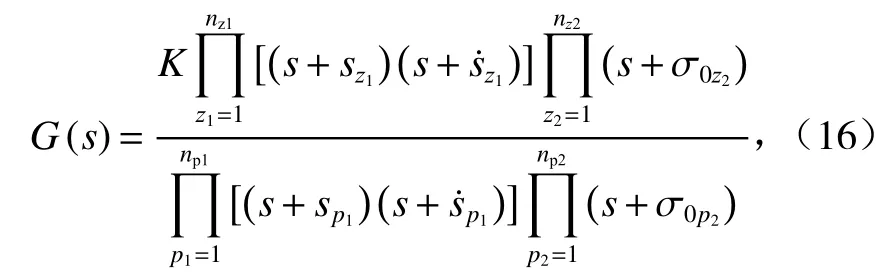
式中：K為比例因子； σ0z2為G(s)的第z2個實數零點；sz1和為G(s)的第z1對共軛復數零點； σ0p2為G(s)的第p2個實數極點；sp1和為G(s)的第p1對共軛復數極點；nz1為G(s)的共軛復數零點的對數；nz2為G(s)的實數零點個數；np1為G(s)的共軛復數極點的對數；np2為G(s)的實數極點個數.

復數極點和零點可以展開為

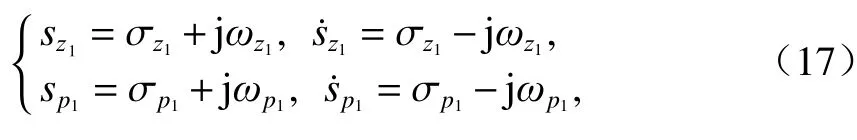
式中： σz1和 jωz1分別為sz1的實部和虛部； σp1和jωp1分別為sp1的實部和虛部.

根據正實函數的性質，有

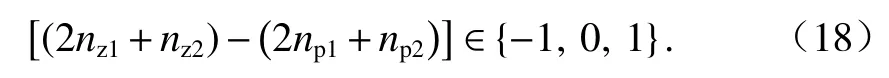
2 懸浮電磁鐵等效電路

懸浮電磁鐵電流的零狀態(tài)響應等于導納Y（s）乘以激勵，因此，I（s）的單位階越響應可以表示為式（19）.

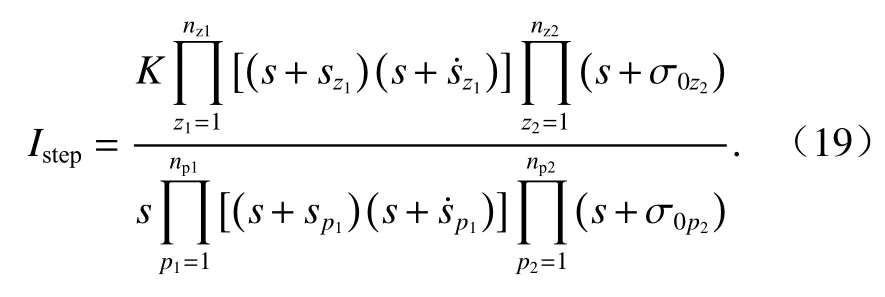
零狀態(tài)的懸浮電磁鐵在單位階躍電壓激勵條件下，繞組的初始電流為0，電壓突變瞬間產生電流振鈴，且電流振鈴逐漸衰減，電流終值為1/Rdc，Rdc為懸浮電磁鐵的直流電阻.由初值定理得

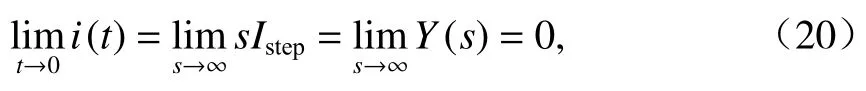
式中：t為時間.

因此，Y（s）的分母多項式的次數高于分子多項式次數.則對于Y（s）有

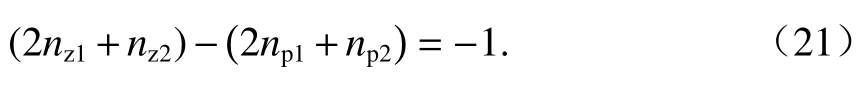
Istep可以展開為

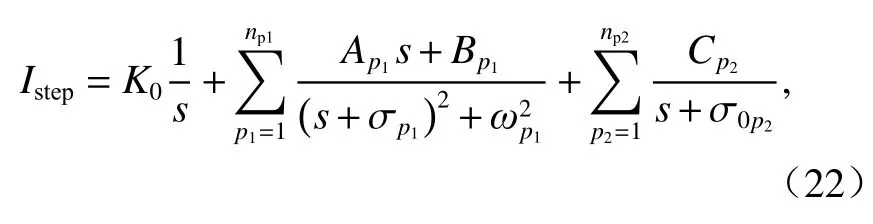
式中：K0、Ap1、Bp1和Cp2均為常系數.

對式（22）進行Laplace反變換得

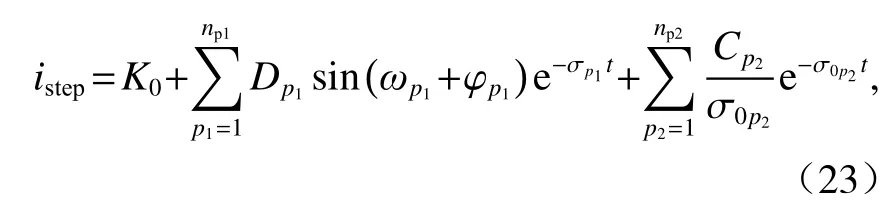
式中：istep為電流單位階躍響應的時域函數；Dp1為常系數； φp1為相位.

Istep的極點類型決定了其時域波形，每個負實數極點對應一項指數衰減波形，每對共軛復數極點對應一項衰減振蕩波形.istep開關動作瞬間的電流振鈴說明Istep至少含有一對共軛復數極點；進一步考慮到istep由初值按指數規(guī)律變化至終值，則Istep的分母多項式中至少含有一個實數極點.綜上所述，Y(s)的最簡表達式中包含3個極點（一對共軛復數極點和一個實數極點）和兩個零點.則Y(s)的最簡表達式為

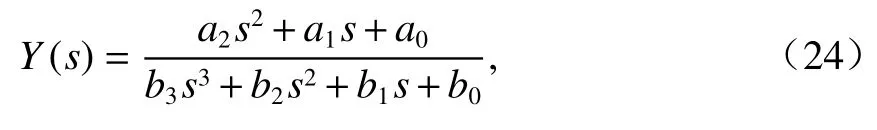
式（24）可以通過圖3所示的電路結構實現.因此可以推斷，圖3所示電路即為懸浮電磁鐵的等效電路模型.

圖3 懸浮電磁鐵等效電路Fig.3 Equivalent circuit of a suspension electromagnet

圖3中：Ceq為懸浮電磁鐵的等效電容；Rac為由絕緣介質損耗引起的高頻等效電阻；Lm為被Ceq旁路的電感；Ls為未被Ceq旁路的電感.其中：Ls、Lm和Rdc構成懸浮電磁鐵的低頻通路，供低頻電流流通；Ls、Ceq和Rac構成懸浮電磁鐵的高頻通路，供高頻振鈴電流流通.Ls和Ceq形成了LC諧振腔，開關動作時刻儲存Ls中的磁場能量和Ceq中的電場能量交換，形成電流鈴，Rac為高頻通路提供阻尼，使Ls和Ceq在能量交換交換過程中損耗衰減.iL和ic分別表示流過懸浮電磁鐵低頻通路和高頻通路的電流.懸浮電磁鐵等效電路中若沒有Ls和Ceq，則不滿足電流振鈴形成條件；若沒有Rac，則電流振鈴幅值不會衰減，因此圖3為包含了電流振鈴特性的懸浮電磁鐵等效電路的最簡配置.式（24）中的系數可以用圖3中電路參數表示為式（25）.

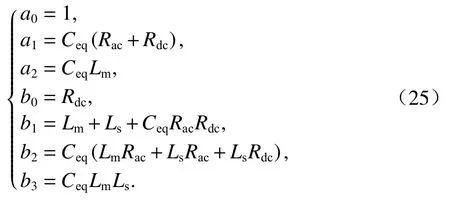
3 不同參數對電流振鈴的影響

根據圖3，懸浮電磁鐵電流振鈴的單位階躍響應可以用式（26）表示.

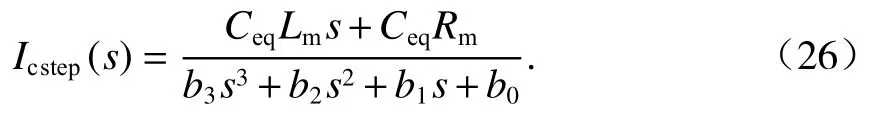
3.1 判別式法分析

由式（26）可知，Icstep(s)的特征方程為

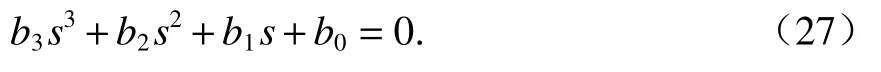
式（27）根值分布的盛金判別式[13]為

當A=C= 0 時，式（27）有一個 3重實根；當Δ＜0時，式（27）有3個不相等的實根；當 Δ =0 時，式（27）有3個實根，其中有1個兩重根；當Δ＞0時，式（27）有1個實根和1對共軛復根，此時懸浮電磁鐵在S1和S2動作瞬間存在振鈴現象.圖4給出了Δ隨不同參數變化的曲線.

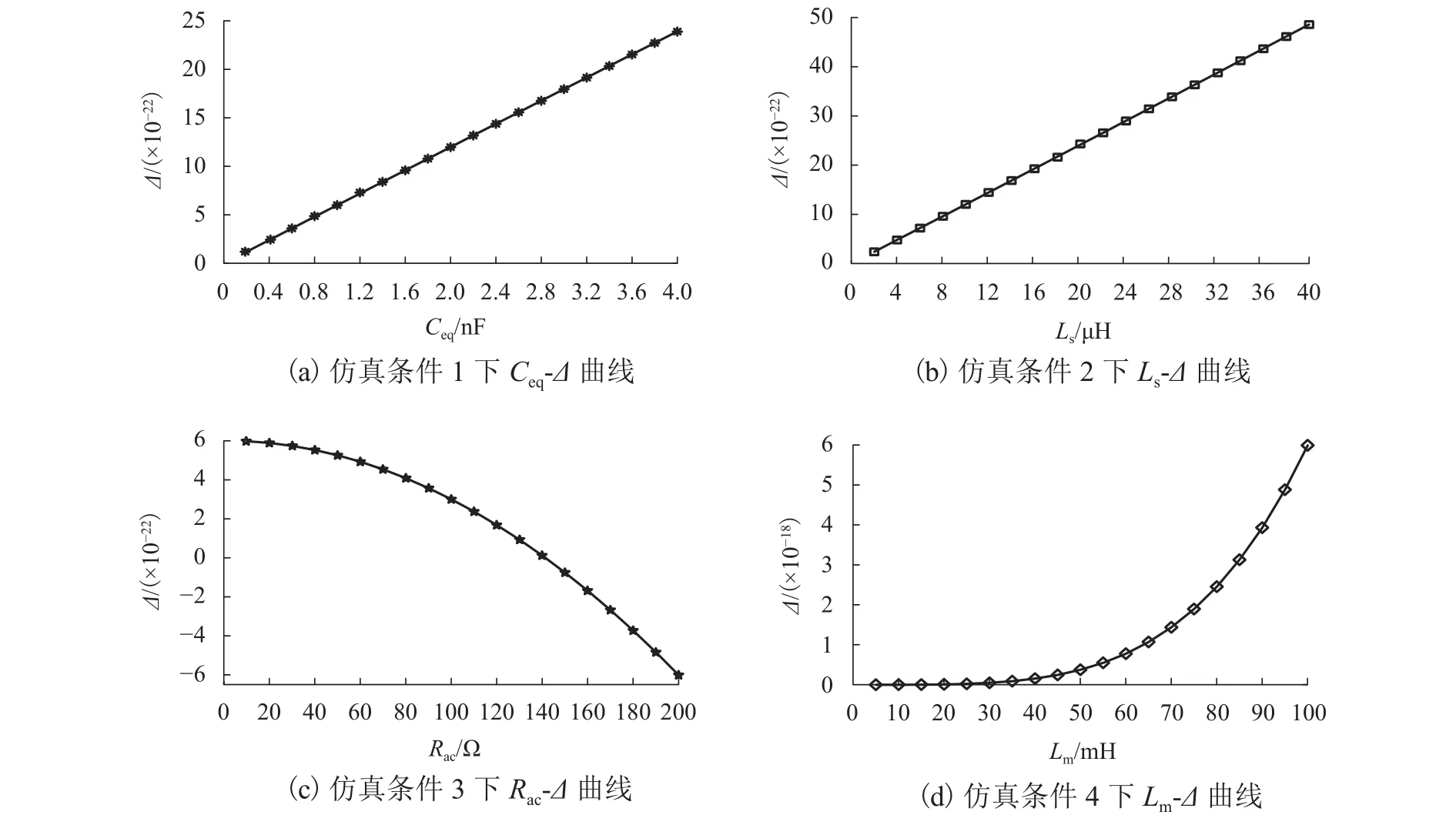
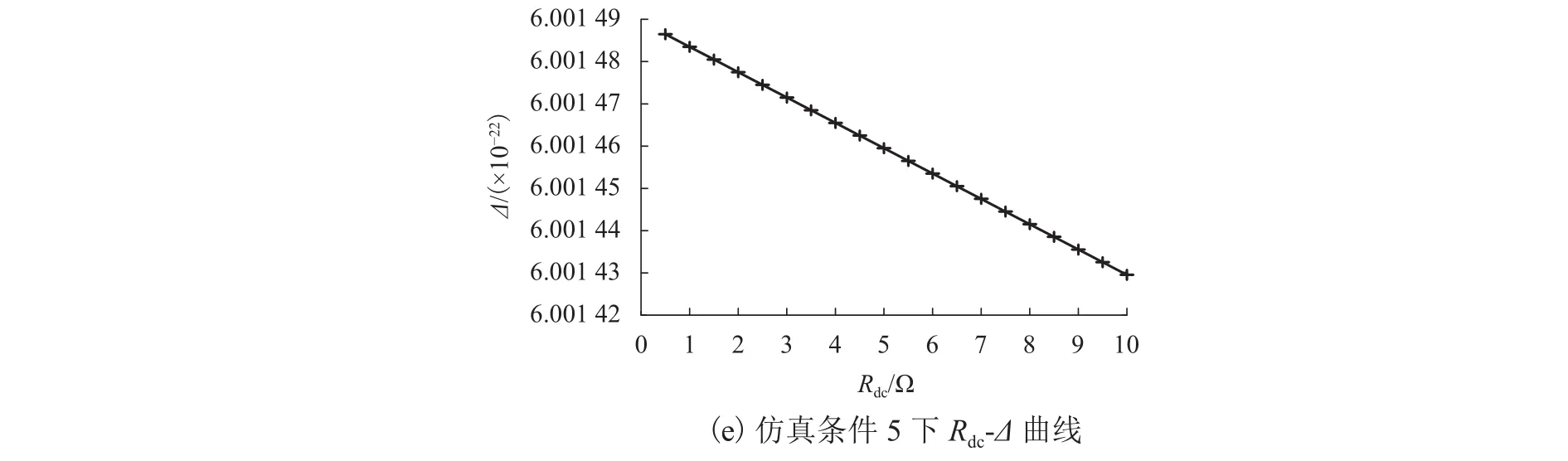
圖4 不同電路參數對Δ的影響Fig.4 Influence of different circuit parameters on Δ

由圖4 可知：在Lm、Rdc、Ls和Rac一定的條件下，Δ隨著Ceq增大而增大；在Lm、Rdc、Ceq和Rac一定的條件下，Δ隨著Ls增大而增大；在Lm、Rdc、Ceq和Ls一定的條件下，Δ隨著Rac增大而減小；在Ls、Rdc、Ceq和Rac一定的條件下，Δ隨著Lm增大而增大；在Ls、Rac、Ceq和Lm一定的條件下，Δ隨著Rdc增大而減小.說明Δ與Ls、Ceq和Lm正相關，與Rac和Rdc負相關.而且，只有在Rac增大過程中，Δ出現負值，即只有在Rac足夠大的條件下，懸浮電磁鐵不存在電流振鈴現象.

3.2 仿真法分析

懸浮電磁鐵電流振鈴仿真模型如圖5所示.其中Iref為目標電流.設計PI電流控制器，使懸浮電磁鐵電流追蹤目標電流.仿真模型中 S1、S2和 D1、D2為理想元件，導通管壓降為0，Iref= 2 A，Udc= 50 V.

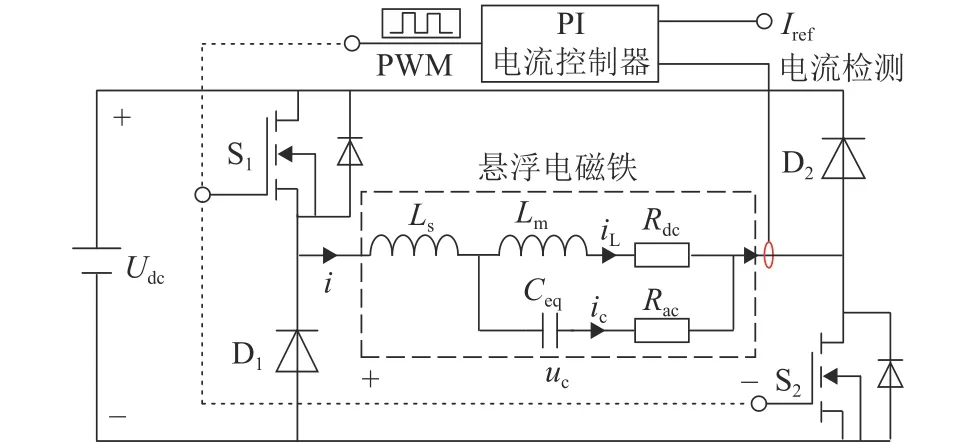
圖5 懸浮電磁鐵電流振鈴仿真模型Fig.5 Current ringing simulation model of a suspension electromagnet

為了研究 Ceq、Ls、Rac、Lm和Rdc對電流振鈴的影響，通過控制變量法進行模型仿真.仿真參數設置如表1所示.各種條件下所得懸浮電磁鐵電流振鈴波形（S1、S2導通時刻）分別如圖6所示.其中：p0表示S1、S2動作前電流的穩(wěn)態(tài)值；p1～p4分別表示不同仿真條件下，變化參數不同取值時瞬態(tài)電流的最大峰值.

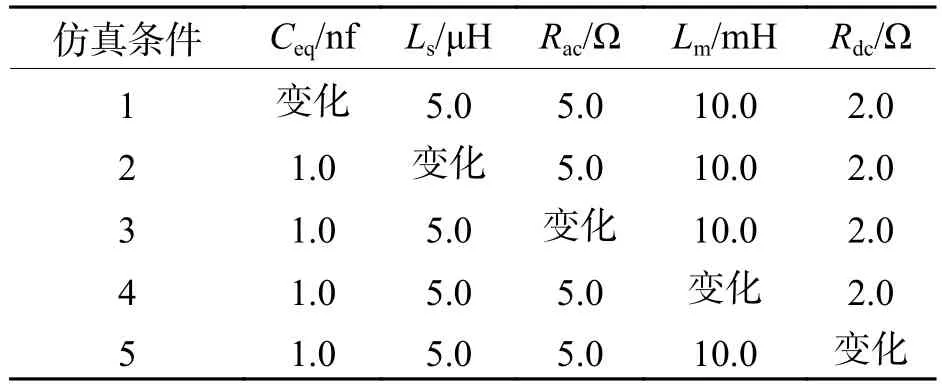
表1 仿真參數設置Tab.1 Sinulation parameter setting

由圖6（a）可知：在仿真條件 1下，Ceq為 0.5、1.0、2.0 nF和4.0 nF時對應的懸浮電磁鐵電流振鈴峰值分別為0.90、1.20、1.90 A和2.50 A，振鈴頻率分別為 3.175、2.222、1.587 MHz和 1.111 MHz.因此，當Lm、Rdc、Ls和Rac一定時，隨著Ceq增大，電流振鈴峰值增加，振鈴頻率減小.此外，Ceq變化對振鈴衰減速度的影響較小.由圖6（b）可知：在仿真條件2下，Ls為 5.0、10.0、20.0 μH 和 40.0 μH 時對應的懸浮電磁鐵電流振鈴峰值分別為1.60、0.95、0.70 A和0.50 A，振鈴頻率分別為 2.222、1.587、1.111 MHz和0.794 MHz.因此，當Lm、Rdc、Ceq和Rac一定時，隨著Ls增大，電流振鈴的峰值減小，振鈴頻率減小；此外，隨Ls增大，振鈴衰減速度減緩.由圖6（c）可知：在仿真條件 3下，Rac為 5.0、20.0 Ω和 50.0 Ω時對應的懸浮電磁鐵電流振鈴峰值分別為1.40、1.20 A和 0.90 A，振鈴頻率均為 2.222 MHz；Rac為 200 Ω時，電流暫態(tài)波形為電流脈沖，峰值為0.40 A.這是由于當Rac為 200 Ω 時，判別式Δ＜ 0.此外，當Lm、Rdc、Ls和Ceq一定時，隨著Rac的增大，電流振鈴幅值減小，振鈴衰減時間縮短.由圖6（d）～（e）可知：電感Lm和電阻Rdc對懸浮電磁鐵電流振鈴峰值、頻率及衰減時間的影響很小.綜上可知：懸浮電磁鐵的電流振鈴特性主要由Ls、Ceq和Rac決定.盡管仿真中所用電路參數可能與實際電路參數不一致，仿真結果仍然可以說明不同參數對電流振鈴的影響.

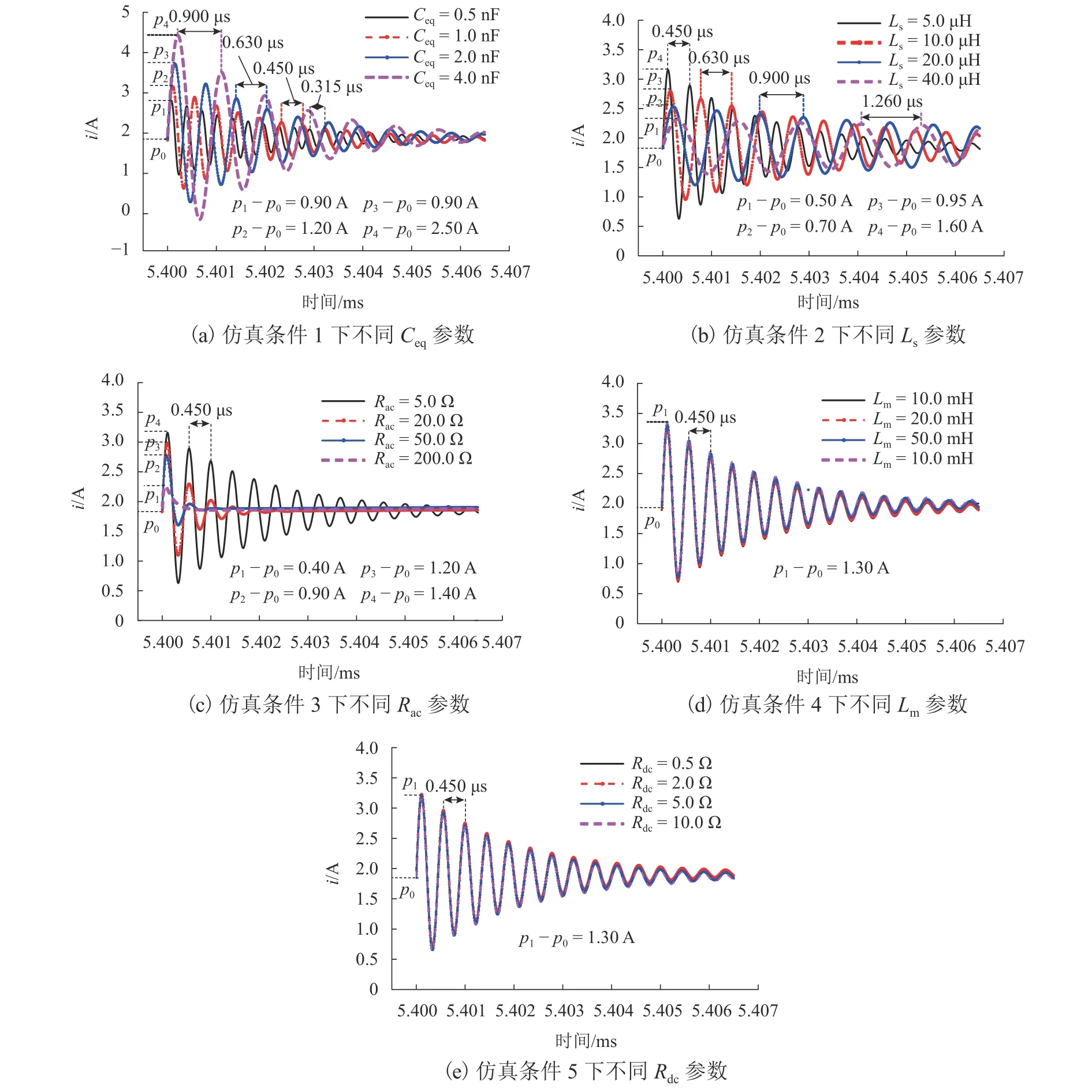
圖6 不同參數條件下懸浮電磁鐵的電流振鈴波形Fig.6 Current ringing waveforms of suspension electromagnet with different parameters

4 小電磁鐵電流振鈴仿真和實驗

懸浮電磁鐵電流振鈴測試系統如圖7所示.用LCR阻抗測量儀測量計算得到懸浮電磁鐵的參數為Lm=6.8 mH，Ceq=308.0 pF，Rdc=1.0 Ω，Ls=3.8 μH,Rac=20.0 Ω.示波器 RTM2032和TSD3054B分別用于觀測懸浮電磁鐵的電壓和電流波形，TCP303和TCPA300分別為電流探頭和電流探頭放大器.懸浮斬波器的 S1、S2采用 IRFP250N 場效應管，D1、D2采用D92-03肖特基二極管，控制器為TMS320 F28335 DSP，PWM驅動器為KA962F模塊.直流母線電壓Udc=50.0 V，目標電流Iref=2.00 A，開關頻率為10 kHz.

圖7 懸浮電磁鐵電流振鈴測試系統Fig.7 Current ringing test system for suspension electromagnet

首先，將上述懸浮電磁鐵的參數代入圖5所示的仿真模型，得到懸浮電磁鐵電流和電壓仿真波形分別如圖8（a）和圖8（b）所示.圖8（a）中：ton為 S1、S2導通時刻；toff為 S1、S2關斷時刻.由圖8（a）可知：仿真所得懸浮電磁鐵電流紋波幅值為0.37 A，S1、S2導通和關斷時刻產生電流振鈴的峰峰值為1.40 A，振鈴頻率約為4.500 MHz.S1、S2導通和關斷時刻所產生電流振鈴的幅值和衰減速度相同，方向相反.由圖8（b）可知：仿真所得懸浮電磁鐵電壓uc為理想的 PWM 波形，S1、S2導通階段，uc= 50.0 V，S1、S2關斷階段，uc= -50.0 V.

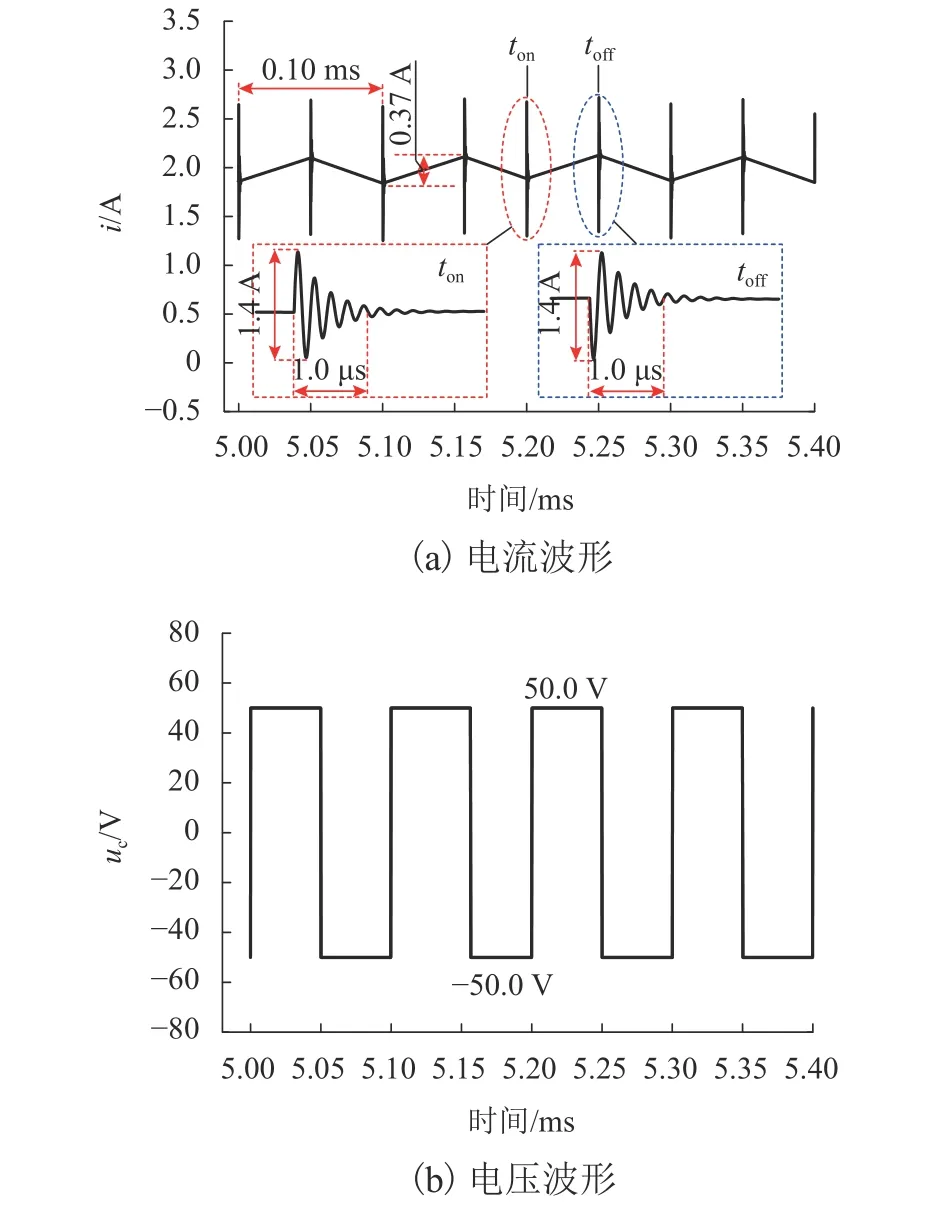
圖8 懸浮電磁鐵電流和電壓的仿真波形Fig.8 Simulated current and voltage waveforms of suspension electromagnet

相同條件下，懸浮電磁鐵電流和電壓實驗波形分別如圖9（a）和圖9（b）所示.由圖9（a）可知：實驗所得懸浮電磁鐵電流紋波幅值為0.33 A，S1、S2導通和關斷時刻產生電流振鈴的峰峰值為1.12 A，振鈴頻率約為4.000 MHz，S1、S2導通和關斷所產生電流振鈴方向相反.由圖9（b）可知：實驗所得懸浮電磁鐵電壓波形在S1、S2導通和關斷時刻存在20.0 V的電壓過沖.此外，S1、S2導通階段，uc的平均值為44.0 V，說明S1和S2的導通管壓降為3.0 V；S1、S2關斷階段，uc的平均值為-47.0 V，說明D1和D2的導通管壓降為1.5 V.

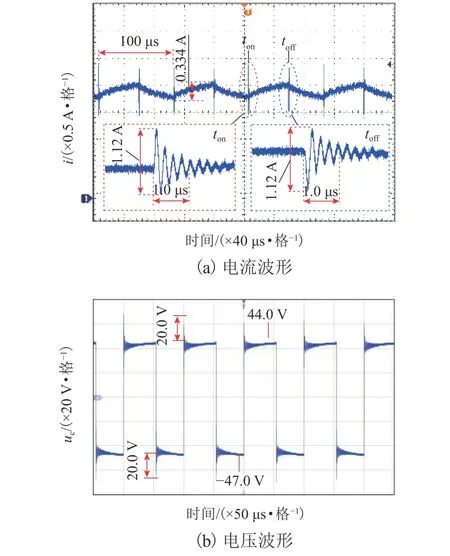
圖9 懸浮電磁鐵電流和電壓的實驗波形Fig.9 Experimental current and voltage waveforms of suspension electromagnet

對比圖9（a）和圖8（a）可知：實驗所得懸浮電磁鐵電流紋波的幅值比仿真結果低9.7%，實驗所得懸浮電磁鐵電流振鈴峰峰值比仿真結果小20%，實驗所得懸浮電磁鐵電流振鈴的頻率比仿真結果低11%.對比圖9（b）和圖8（b）可知：實驗所得懸浮電磁鐵電壓波形在S1、S2動作時刻存在電壓過沖，而仿真結果不存在電壓過沖.這是由于仿真模型忽略了S1、S2和D1、D2的導通壓降、導通等效電阻、封裝寄生電感以及印制電路板電路寄生電感的影響[14].此外，S1、S2的寄生電容（門極-漏極寄生電容、門極-源極寄生電容和漏極-源極寄生電容）和D1、D2的結電容也會對高頻振鈴信號產生影響[15].

5 結 論

本文用策動點函數法推導了懸浮電磁鐵導抗函數的一般形式，并提出了一種考慮電流振鈴特性的懸浮電磁鐵等效電路模型.

所提等效電路模型包含低頻和高頻兩種電流通路.流振鈴分量主要從高頻通路流通，振鈴的幅值特性、頻率特性和衰減特性由高頻通路的等效電感、等效電阻和等效電容決定.

所提懸浮電磁鐵等效電路模型可用于仿真和分析懸浮斬波器的暫態(tài)特性，也能為懸浮電磁鐵電流振鈴抑制方案設計提供指導.

由于開關器件寄生電感、寄生電容以及印制電路板線路寄生電感等未建模因素的影響，所提等效電路與實際電路之間存在一定偏差.因此，為了提高模型的準確性，應進一步建立包含上述參數的等效電路模型.此外，可進一步根據所提等效電路設計適用于電磁懸浮系統的電流振鈴抑制裝置.