震源深度對二維盆地放大的影響研究*

邵祖鵬，劉啟方

(蘇州科技大學 江蘇省結構工程重點實驗室，江蘇 蘇州 215009)

0 引言

國內外多次大地震的震害經驗和相關研究表明，沉積盆地對其內部的地震動有顯著的放大效應，進而導致盆地內的災害更加嚴重，如1994年美國北嶺地震中的洛杉磯盆地(Pitarka，Irikura，1996)和2002年臺灣花蓮近海地震中的臺北盆地(Chen，2003)。因此，針對盆地地震放大作用，地震工程研究者開展了大量的研究。Kawase和Aki(1989)認為，在1985年墨西哥地震中，在墨西哥城觀察到的極長地震動持時可能是由軟表面層與城市下方深盆結構的強烈相互作用造成的。Kawase(1996)對1995年日本神戶地震的研究表明，一個中等強度的地震即可引起盆地內部極具破壞性的強地震動。

諸多研究表明盆地傾角、震源深度、盆地內外介質阻抗比(于彥彥等，2020)等參數對地震放大作用有較顯著影響。劉啟方等(2013，2020)利用三維施甸盆地模型及川滇地區的地殼速度結構，研究得到盆地內覆蓋層厚的區域地震動強度大于覆蓋層薄的區域，并采用譜元法模擬了1556年華縣地震時渭河盆地0.02～0.5 Hz地震波的傳播過程，發現盆地的深厚土層對于4 s以上的地震動有著明顯的放大作用。禹樂等(2020)采用譜元法及PML邊界條件，研究了內置點源下盆地傾角對地表地震動時、頻域放大特征的影響。劉中憲等(2017)基于譜元法和動力學震源模型研究了盆地內外介質的波速比對地表地震動時程和峰值的影響。李雪強(2011)建立了一系列具有不同傾角、不同沉積層厚度、不同介質阻抗比的理想盆地模型，并利用波動有限元數值模擬方法，研究了以上因素對盆地的影響。丁海平等(2018)利用譜元法，通過分析盆地模型與均勻半空間模型中觀測點的速度時程、峰值和放大系數，研究了盆地傾角、盆地深度對盆地地震效應的影響。但以往對于盆地內部地震動放大效應的研究多采用場地外單一平面體波入射或面波入射(陳學良等，2011；張建經等，2014；郭明珠等，2004)，而實際入射到盆地的地震波則是體波和面波兼有。且以往采用譜元法模擬二維盆地的模型大多研究單一參數對盆地效應的影響，模擬工況較為單一。因此，本文基于譜元法，采用4種不同傾角盆地模型，研究了不同震源深度下走滑地震非平面波入射時，二維盆地的放大規律，分析了盆地邊緣放大的峰值及其位置與無量綱頻率、阻抗比和盆地傾角的關系。

1 計算模型及方法

1.1 計算模型

采用梯形盆地模型，盆地角度分別取15°、30°、45°和60°。計算模型長度方向為45 km，深度方向為18 km，如圖1所示。盆地長10 km，深0.5 km，在盆地內部及盆地左右兩側2 km處每隔50 m布置一個觀測點，共281個等間距觀測點。因觀測點過多，圖1中每隔1 km顯示一個觀測點。

圖1 計算模型及觀測點位置Fig.1 Calculation model and the position of observing points

為了分析不同震源對應的不同方向入射波的影響，取4個不同的震源，震源深度分別為2.68、5.77、10.00和17.32 km。和代表不同震源下盆地入射波的角度范圍，見表1。盆地內外的介質參數見表2，、和分別表示盆地外基巖的剪切波速、密度和品質因子，、和則為盆地內相應參數。本文取盆地內外剪切波速分別為400 m/s和1 500 m/s，盆地內外介質的阻抗比為3.75。

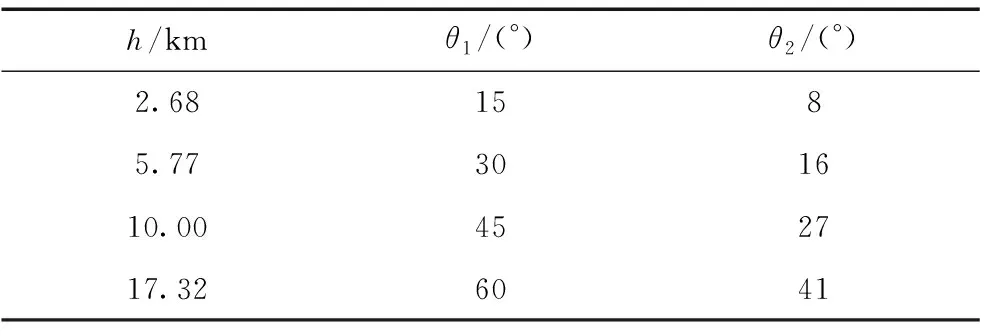
表1 震源深度h及入射角范圍θTab.1 Focal depth h and the range of incident angle θ

表2 盆地模型介質參數Tab.2 Media parameters of the basin model

1.2 計算方法

目前模擬地震波在沉積盆地中傳播的方法主要有限差分法、有限元法、邊界元法以及譜方法。近年來，隨著 Komatitsch 和 Vilotte(1999)將譜元法推廣到地震波場的模擬并推出適用于二維和三維問題的譜元程序 SPECFEM2D 及 SPECFEM3D，其作為一種高精度(廖樹超等，2018)的數值方法得到越來越廣泛的應用(嚴珍珍等，2009；Komatitsch，2012)。

本文采用二維譜元程序SPECFEM2D進行計算，盆地內、外網格尺寸分別為40 m和80 m。模擬時間步長為0.001 s，共計模擬40 000步。本文采取4階譜元格式，模擬計算頻率至=4。震源取=4.0的點源，走向90°、傾向45°、滑動角0°，地震矩張量中除為1.26×10dyne·cm外，其余==0。震源時間函數采用Ricker子波，圖2給出了中心頻率為0.4 Hz的Ricker子波速度時程及傅立葉譜。

圖2 中心頻率為0.4 Hz的Ricker子波速度時程(a)及傅立葉譜(b)Fig.2 The velocity time history(a)and the Fourier spectrum(b)

本文采用無量綱頻率分析盆地的放大與幾何形狀、盆地內外介質阻抗比和輸入角度的關系。無量綱頻率代表盆地的深度和入射Ricker子波中心頻率對應的波長之比，定義為：

==×

(1)

式中：為盆地深度；為波長；為Ricker子波主頻。本文采用不同中心頻率Ricker子波的震源時間函數，分析不同的影響。本文用到的參數為：=0.125、0.25、0.5、1、2、4；盆地傾角=15°、30°、45°、60°；阻抗比=3.75。

of Ricker wavelet with center frequency of 0.4 Hz

2 數據分析

由于采用Ricker子波作為震源時間函數，激發的地震波主要位于中心頻率附近，因此本文采用同一無量綱頻率下，分別計算盆地模型和基巖半空間模型的各點的速度時程的峰值。圖3為阻抗比3.75、=0.25下的45°傾角盆地速度時程及。從圖中可以看到，P波首先進入盆地，然后是S波；盆地內地震動持時顯著增長，顯著增大。本文定義盆地模型和基巖半空間模型各點速度時程的峰值之比，為該無量綱頻率下的放大。

圖3 45°傾角盆地速度時程(a)及PGV(b)Fig.3 Velocity time history(a)and PGV(b)of the basin with dip angle 45°

圖4給出了震源深度為10 km，阻抗比為3.75時，6種無量綱頻率下，4種傾角盆地模型水平向和豎直向的盆地和基巖半空間的速度峰值比，該震源深度下，盆地入射波范圍是27°～45°。筆者對圖像進行歸一化處理，取盆地中心點為原點，設定為盆地寬度的一半(5 km)，為變量，在盆地最左側即=-1，為盆地傾角。

由圖4可見：①在水平和豎直方向，隨著的增大，速度峰值比由非常平滑轉向局部振蕩，特別是在盆地邊緣附近。②在豎直方向，盆地邊緣速度峰值也呈現較大的值。這表明盆地邊緣不僅會出現強烈的橫向振動，還會出現劇烈的垂直運動。③較大時，盆地兩側邊緣的地面運動變化比較劇烈，這是因為高頻的入射波與盆地邊緣相互作用更強，從而影響較短距離上的地面運動特征。這與Ayoubi(2020)的研究結果相同。④增大后，15°傾角盆地模型的速度峰值比突變較大，與其它角度的盆地模型的速度峰值比形成鮮明對比，這可能是因為15°傾角盆地比其他角度的盆地有著更長的斜邊。丁海平等(2018)發現盆地邊緣傾角較小時，盆地邊緣對地震動的放大效應更強(ricker子波中心頻率為5 Hz)，與本文結果一致。盆地中心區域受傾角影響相對較小，禹樂(2020)也有類似的研究成果。

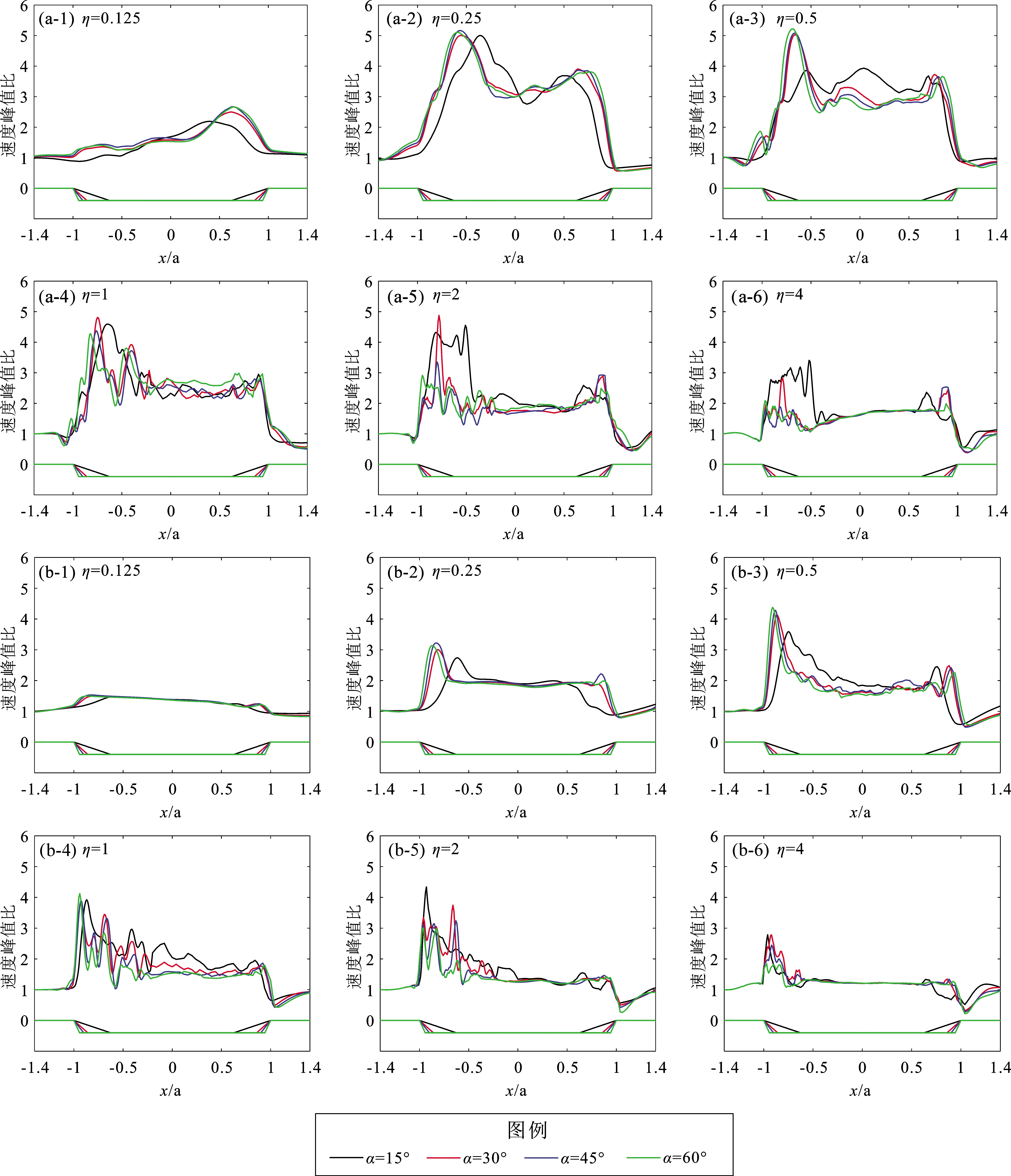
圖4 在6種無量綱頻率下4種盆地傾角模型水平向(a)和豎直向(b)的速度峰值比分布Fig.4 Distribution of the ratios of peak velocity in horizontal(a)and vertical(b)direction at six dimensionless frequencies for four basin models with different dip angles

為研究不同無量綱頻率在單一傾角盆地下速度峰值比的大小，圖5給出阻抗比為3.75時，不同無量綱頻率下45°傾角盆地水平向和豎直向的速度峰值比。由圖5可見：①隨著的增大，速度峰值比在=0.5時達到最大值，然后衰減。即當≤0.5時，速度峰值比變大；當>0.5時，速度峰值比逐漸減小。②對于較低的，入射波將盆地視為一個整體，放大很小；隨增大，入射波與盆地局部相互作用增強，地震動也更為復雜。

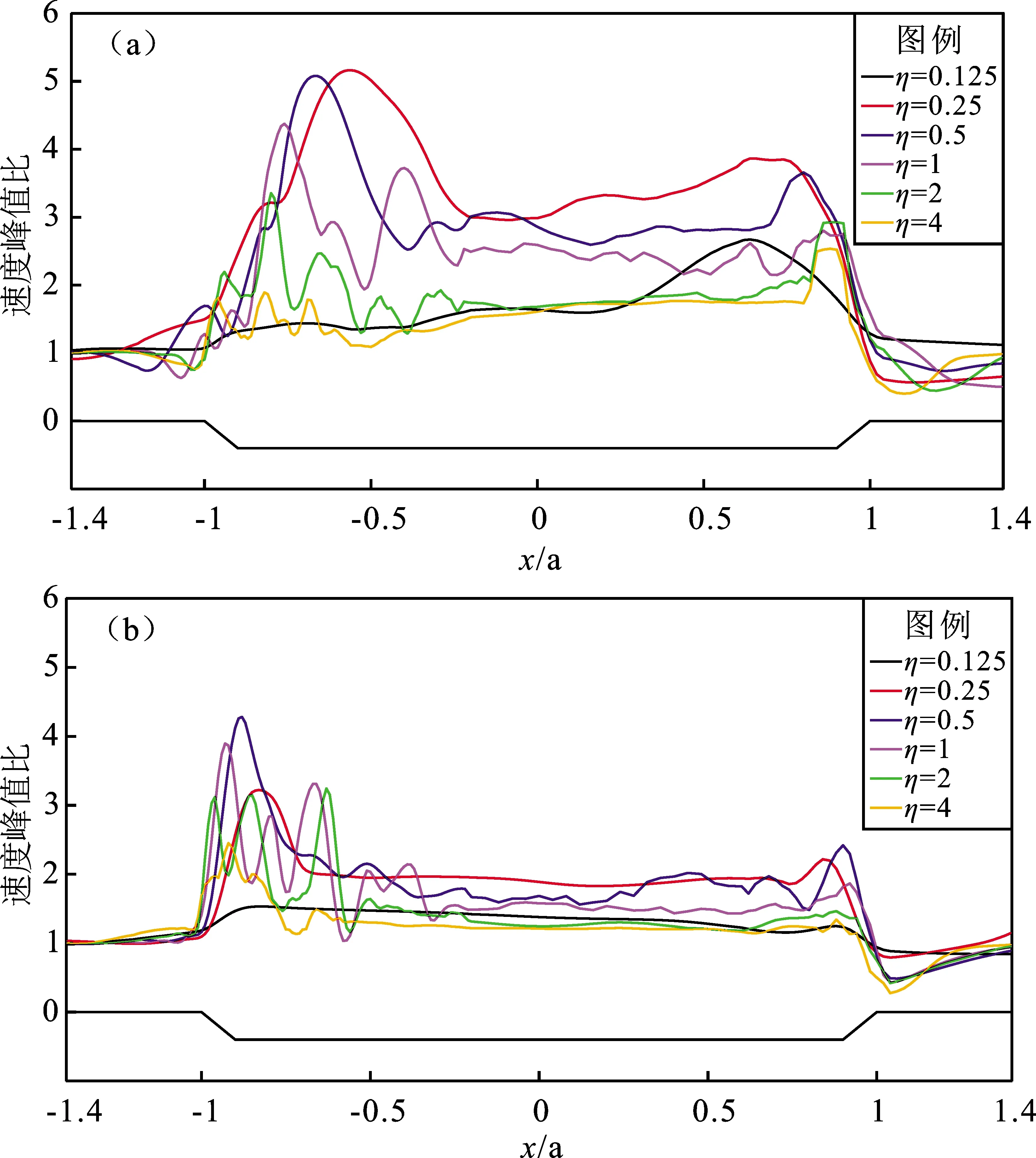
圖5 45°傾角盆地的水平向(a)和豎直向(b)速度峰值比Fig.5 The ratio of peak velocity in the horizontal(a)and vertical(b)direction of the basin model with dip angle 45°

為了探討速度峰值比最大值變化的規律，圖6給出了阻抗比為3.75時，不同震源深度下4種傾角盆地速度峰值比最大值隨的變化。由圖6可見：①隨著震源深度的增大，4種傾角盆地水平方向速度峰值比最大值逐漸增大，在震源深度為10 km時達到最大，隨后減小。震源深度較淺時(2.68 km和5.77 km)，4種傾角盆地水平方向速度峰值比最大值相差不大，差值始終小于1。震源深度較深時(10 km和17.32 km)，4種盆地的速度峰值比最大值在≤0.5時相差不大，在≥1時相差很大。如圖6c所示，=2時60°傾角盆地的速度峰值比值為2.6，15°傾角盆地的值為4.5，后者約為前者的1.73倍；=4時45°傾角盆地的速度峰值比的值為1.8，15°傾角盆地的值為3.5，后者是前者的兩倍左右。②水平方向上的速度峰值比最大值為1～5.3，豎直方向為1～5。整體來看，隨著增大，水平向和豎直向速度峰值比最大值也增大，于為0.5～1時達到最大，隨后減小。

圖6 不同震源深度下4種不同傾角盆地速度峰值比最大值隨η變化Fig.6 The maximum ratio of peak velocity of basin models with four dip angles varies with η at different focal depth

為了探討影響速度峰值比最大值位置的因素，圖7給出了阻抗比為3.75時，不同震源深度、不同下4種不同傾角盆地速度峰值比最大值的位置。由圖7可見：①同一震源深度下，隨著增大，速度峰值比的最大值的位置逐漸偏向盆地邊緣。豎直方向上，當震源深度為10和17.32 km時，隨著盆地傾角的增大，最大值的位置偏向盆地邊緣。水平方向上，當≥2，震源深度為2.68、5.77和10 km時，隨著盆地傾角的增大，最大值的位置偏向盆地邊緣。②當震源深度為2.68、5.77和10 km時，不同下15°傾角盆地速度峰值比最大值的位置相比另外3種傾角盆地更偏向盆地中心。當震源深度為2.68 km、=2時，15°傾角盆地的速度峰值比的最大值的位置與盆地邊緣的距離是60°傾角盆地的3.7倍。當震源深度逐漸增大時，水平向和豎直向速度峰值比最大值的位置逐漸偏向盆地邊緣。

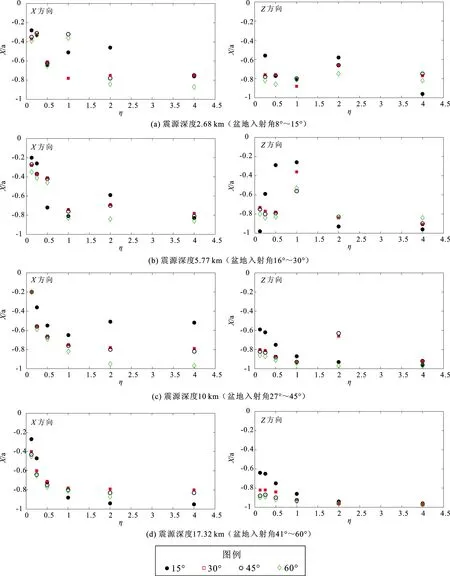
圖7 不同震源深度、不同η下4種不同傾角盆地速度峰值比最大值所在盆地位置Fig.7 Location of the maximum ratio of the peak velocity of basin models with four dip angles in frequencies η at different focal depth

3 結論

本文基于二維譜元法，采用4種不同傾角盆地模型，研究不同震源深度走滑地震非平面波入射時，二維盆地的放大規律，分析了盆地邊緣放大的最大值及其位置與無量綱頻率和盆地傾角的關系，主要得出以下結論：

(1)水平方向速度峰值比的最大值為1～5.3，豎直方向為1～5。盆地邊緣處豎直方向速度峰值比也呈現較大的值，這表明盆地邊緣也會出現劇烈的垂直運動。隨著震源深度的增大，水平方向速度峰值比的最大值逐漸增大，在震源深度為10 km時達到最大，隨后減小，水平向和豎直向速度峰值比的最大值的位置逐漸偏向盆地邊緣。

(2)震源深度較淺時，4種傾角盆地在水平方向上的速度峰值比的最大值大小相差不大，差值始終小于1；震源深度較深且較高時(≥1)，4種傾角的盆地的速度峰值比相差很大，最大差值達到3。豎直方向上，震源深度較淺時，隨著盆地傾角的增大，速度峰值比的最大值的位置偏向盆地邊緣。水平方向上，震源深度較淺且較高時，隨著盆地傾角的增大，速度峰值比的最大值的位置偏向盆地邊緣。

(3)同一震源深度下，越大，速度峰值比最大值的位置也更接近盆地邊緣。對于較低的，入射波將盆地視為一個整體，放大很小。隨著的增大，入射波與盆地局部相互作用增強，放大倍數(水平向和豎直向)將明顯增加。當無量綱頻率到達一定值后(≥1)，放大倍數開始逐漸減小。同一震源深度下，越大，速度峰值比最大值的位置越偏向盆地邊緣。

需要說明的是，本文的結果由對特定盆地形狀、尺寸、阻抗比及特定震源等的研究得出，以上因素對盆地地震響應均有顯著影響，若相應參數改變，對盆地效應影響的差異性也會顯現，這還需要開展進一步的研究。