通信輔助衛星導航接收機最優捕獲靈敏度分析

王 雷，雷長彪

(中國人民解放軍32082部隊，北京 100191)

0 引言

我國北斗三號全球衛星導航系統已于2020年完成全星座組網，提供全球定位服務。但更高性能的衛星導航定位需求仍然在不斷增長，因此，準確分析當前衛星導航系統的具體能力，對于未來發展新一代的衛星導航系統具有很好的指導作用。

本文關注通信輔助下衛星導航接收機的捕獲靈敏度結果。在衛星導航信號捕獲階段，通信輔助可以提供初始定位導航與授時(Positioning Navigation and Timing，PNT)信息，以降低捕獲復雜度，提高捕獲靈敏度。

捕獲算法是一個偽碼相位和載波多普勒的二維搜索過程，通信輔助通過提供包括接收機位置、衛星星歷以及接收機時間等信息，有助于降低捕獲中的頻率不確定度以及時延不確定度，進而接收機可通過改進算法提升靈敏度。文獻[3]對不同輔助信息精度下的頻率搜索范圍壓縮程度和偽碼相位壓縮程度進行了分析。在此基礎上對算法進行改進，以提高捕獲靈敏度，文獻[4]分析了輔助信息與捕獲靈敏度提升量之間的關系，但是僅得出了極限的性能結果，并未考慮由此導致的計算復雜度提升。衛星導航信號捕獲靈敏度是在滿足系統捕獲概率和虛警概率條件下所能捕獲到的信號的最低載噪比，捕獲靈敏度越高，意味著可接收的信號載噪比越低。為提高接收機捕獲靈敏度，普遍的做法是提高相干積分時長以及非相干累加次數，從而提高相關增益。

捕獲算法的兩個評價標準為平均捕獲時間和計算復雜度，部分文獻以平均捕獲時間為優化目標對算法進行改進，并分析了輔助條件下平均捕獲時間的降低情況。

但目前并未有文獻給出不同輔助信息條件下捕獲靈敏度的具體結果，本文通過約束平均捕獲時間以及計算復雜度指標，對捕獲靈敏度與輔助信息精度之間的定量關系進行分析。

1 捕獲算法性能評價指標

評價捕獲算法的兩個主要指標是平均捕獲時間和捕獲算法復雜度。

1.1 平均捕獲時間

平均捕獲時間反映的是衛星導航接收機完成信號捕獲所需的平均時長，文獻[8-9]給出了并行搜索條件下接收機平均捕獲時間的表達式，如式(1)所示

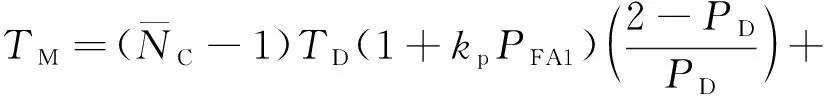
(1)

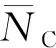
=1-(1-)=1-(1-)-1

(2)

其中，為單次并行搜索完成的單元數量。

在算法保持不變的情況下，平均捕獲時間隨搜索范圍的減小而降低。相應地，接收機可在平均捕獲時間滿足指標的條件下改善捕獲算法，從而實現提高捕獲靈敏度的效果。

1.2 捕獲算法計算復雜度

捕獲算法的計算復雜度反映的是完成捕獲運算所需的計算資源情況。以時域并行快速傅立葉變換(Fast Fourier Transform，FFT)捕獲算法為例，其實現框圖如圖1所示。

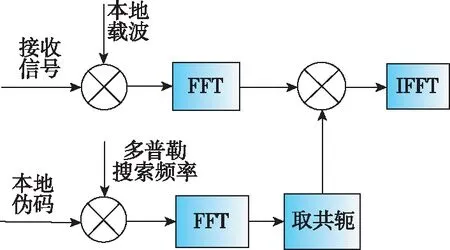
圖1 時域并行FFT算法實現框圖

時域并行FFT捕獲算法利用FFT運算實現偽碼相位的并行搜索，是一種高效的捕獲算法。為保證FFT算法的效率，通常將運算點數取2的整數次冪，以表示相干積累采樣點數，表示碼相位搜索點數，則FFT運算點數表示為

=2(+)

(3)

其中，2()為距離最近的下一個2的整數次冪。

以表示頻率搜索單元數量，則時域并行FFT捕獲算法的計算復雜度如表1所示。

表1 時域并行FFT捕獲算法計算復雜度

其中對于現場可編程門陣列(Field Programma-ble Gate Array,FPGA)等計算器而言，乘法器計算復雜度遠高于加法器，因此在分析計算復雜度過程中主要考慮乘法器計算量。

以常用的民用導航信號為例，對計算復雜度進行分析，設定偽碼速率為1.023MHz，偽碼搜索范圍為1ms，載波多普勒搜索范圍為±5kHz，頻率搜索間隔取1(2)，其中為相干積分時長，不同相干積分時長條件下的計算復雜度結果如圖2所示。

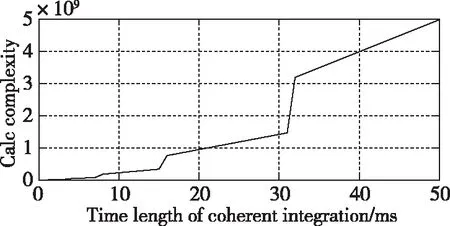
圖2 計算復雜度與相干積分時長的量化關系

由圖2可知，捕獲算法計算復雜度隨信號相干積分時長的增加而逐漸增長，其中急劇增長的部分是由于FFT運算點數升級至下一個2的整數次冪；同時，受制于有限的運算器件計算資源，相干積分時長并不能無限制提高。通過上述分析可知，計算復雜度對于捕獲靈敏度起著制約作用。

2 輔助接收機捕獲靈敏度評估方法

根據上述分析可知，在平均捕獲時間和計算復雜度的約束下，輔助信息與最優捕獲算法以及可實現的捕獲靈敏度之間存在特定對應關系。為明確其定量結果，本文定義輔助接收機捕獲靈敏度評估方法，對于由相干積分以及非相干累加組成的捕獲算法，其表達式如式(4)所示

(4)

其中，為頻率搜索范圍；為偽碼相位搜索范圍；為相干積分時長；為非相干累加次數；為信號載噪比；為平均捕獲時間門限；為捕獲概率門限；為虛警概率指標；為計算復雜度指標門限。

由于導航信號偽碼周期通常為整毫秒，因此在本文分析中，將相干積分時間取為整數毫秒。在上述條件下，本文在一定范圍內對相干積分時長和非相干累加次數進行遍歷，從而獲得該評估方法下的捕獲算法最優解。

其計算流程如下：

1)首先根據計算復雜度指標，確定相干積分時長的取值范圍；

2)在一定范圍內，對、進行遍歷，找出使得捕獲算法同時滿足式(4)中所有約束的、值，對應于最低載噪比的值即為最優捕獲算法的捕獲參數，相應的載噪比值為最優的捕獲靈敏度值。

3 捕獲算法損耗分析

在上述分析中，給出了輔助接收機捕獲靈敏度評估方法，為定量地分析捕獲靈敏度與捕獲算法的關系，對捕獲算法的損耗需采用盡量精確的模型。本文在分析捕獲算法損耗的過程中，對于偽碼損耗考慮偽碼相位與偽碼多普勒損耗，對于載波損耗考慮載波多普勒和載波多普勒變化率損耗。以導航信號中主用的二進制相移鍵控(Binary Phase Shift Keying，BPSK)信號體制為例，相關損失表達式如下所示。

1)偽碼損耗

存在偽碼多普勒的情況下，相關損耗表達式如式(5)所示

(,)=

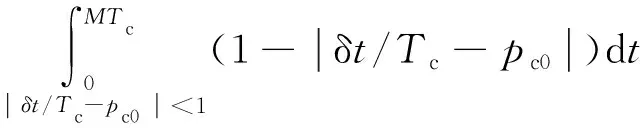
(5)

其中，為偽碼頻率變化率，偽碼多普勒與以及偽碼碼率的關系為=；為偽碼初相；為碼片寬度；為相干積分時長內的碼片數量。

2)載波損耗

當同時存在載波多普勒以及載波二階多普勒的情況下，載噪比損耗表達式如式(6)所示

(,,)=

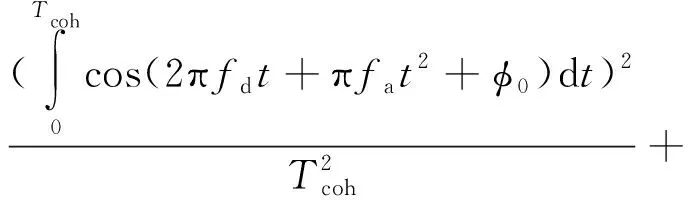
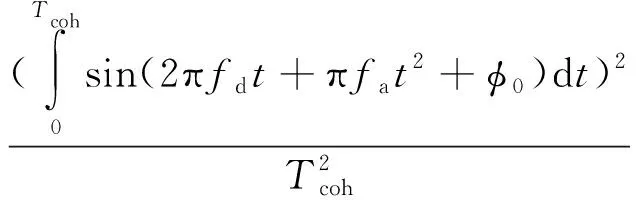
(6)

其中，為多普勒頻率；為載波多普勒變化率；為初始載波相位偏差。

在采用平方律檢波的條件下，基于上述損耗模型可以得出精確的檢測統計量概率分布函數，據此可計算出不同、以及條件下的捕獲概率與虛警概率。

4 評估結果

根據上述分析過程中建立的評估方法以及分析模型，以典型的車載設備和機載設備為例，對輔助接收機捕獲靈敏度結果進行分析。

信號的動態包括衛星運動產生的動態、接收機鐘差產生的動態以及載體運動產生的動態，北斗中地球軌道(Medium Earth Orbit, MEO)衛星對地面靜止目標的最大相對速度為700m/s，衛星導航接收機中常用的溫度補償性晶振的頻率準確度為10～10。

取不同載體類型的一組動態典型值作為輔助接收機捕獲靈敏度的分析條件，具體如表2所示。

表2 載體動態典型值

結合接收機時鐘性能，在不同類型載體動態典型值下，所接收衛星導航信號的動態典型值如表3所示。

表3 不同類型載體信號動態典型值

載體信號動態典型值不僅表示了信號捕獲過程中載波多普勒的搜索范圍，同時，多普勒變化率也是影響衛星導航信號捕獲算法性能的重要因素。

4.1 靈敏度分析結果

在當前接收機設計過程中，受導航電文長度限制，相干積分時長通常不會超過20ms，為代表大多數接收機的具體情況，本文考慮算法復雜度約束下捕獲算法的相干積分時長最長為20ms。

接下來，本文基于通信輔助接收機捕獲靈敏度評估方法對捕獲靈敏度與偽碼相位搜索范圍壓縮和頻率搜索范圍壓縮之間的關系進行分析。在分析過程中，以偽碼相位和載波頻率最大的搜索范圍作為基準值，在基準值的基礎上進行壓縮，分析捕獲靈敏度與壓縮程度之間的具體關系。

經分析，不同載體類型條件下不同偽碼速率信號的捕獲靈敏度與偽碼相位搜索范圍壓縮量之間的關系如圖3所示。

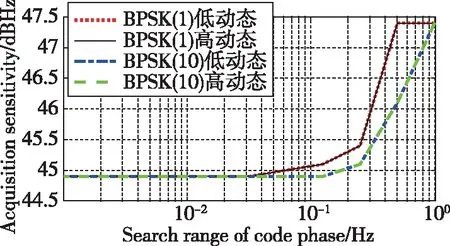
圖3 捕獲靈敏度與偽碼相位搜索范圍壓縮量的量化關系

不同載體類型條件下不同偽碼速率信號的捕獲靈敏度與頻率搜索范圍壓縮量的量化關系如圖4所示。

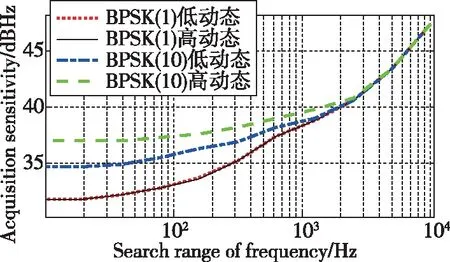
圖4 捕獲靈敏度與頻率搜索范圍壓縮量的量化關系

根據上述分析，可以得出如下結論：

1)相同的壓縮比例下，偽碼相位壓縮產生的靈敏度提升量小于頻率壓縮量，這與具體的捕獲算法相關。本文分析過程中選用的捕獲算法為并行偽碼相位搜索算法，在偽碼相位搜索上進行了壓縮，因此進一步壓縮對于算法產生的效益較小。若捕獲算法采用的是串行搜索算法或者并行頻率搜索算法，本結論會存在差異。

2) 對于BPSK(10)信號，偽碼相位搜索范圍在基準值基礎上壓縮至1/2的過程中，靈敏度提升量約1.3 dB，在搜索范圍壓縮至基準值1/4的過程中，靈敏度提升量約2.3dB；而對于BPSK(1)信號，搜索范圍壓縮至初始值1/4的過程中，靈敏度提升量約2.0dB。

3) 頻率搜索范圍在基準值基礎上壓縮至1/2的過程中，靈敏度提升量約4dB；在搜索范圍壓縮至基準值1/4的過程中，搜索靈敏度提升量約7dB。

4)隨著輔助條件下頻率搜索范圍壓縮程度的增加，每壓縮1/2捕獲靈敏度提升量逐步降低，達到1/32的情況下，每壓縮1/2捕獲靈敏度提升量開始低于1dB。

根據上述分析可知，在本文考慮的算法條件下，頻率搜索范圍壓縮對于捕獲靈敏度的提升要優于偽碼相位搜索范圍壓縮的效果。

在上述分析過程中， 捕獲概率、虛警概率指標為確定值，但在接收機設計過程中，通常會根據需求對捕獲概率和虛警概率進行設置。因此，接下來分析在不同的捕獲概率和虛警概率指標下，輔助接收機捕獲靈敏度與頻率搜索范圍壓縮度的量化關系，具體結果如圖5所示。

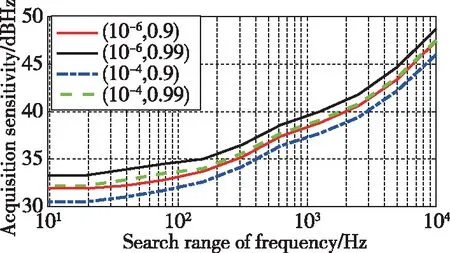
圖5 不同捕獲概率、虛警概率條件下捕獲靈敏度與頻率搜索范圍壓縮量的量化關系

根據上述分析可知，在不同的虛警概率和捕獲概率指標下，相同的頻率搜索范圍對應的捕獲靈敏度略有差異，但相同的頻率搜索范圍壓縮量下捕獲靈敏度提升量基本相同。

由此可知，在一定范圍內捕獲概率和虛警概率指標對輔助接收機捕獲靈敏度提升量影響較小。因此，通過本文方法得到的輔助接收機捕獲靈敏度提升量，對不同指標下的接收機設計具有一定的普適性。

4.2 捕獲算法最優參數

根據上述分析，不同條件下的最優算法參數情況如表 4和表 5所示，分析可知：

表4 輔助接收機不同偽碼相位搜索范圍壓縮量下捕獲算法最優參數(Tcoh,Nncoh)

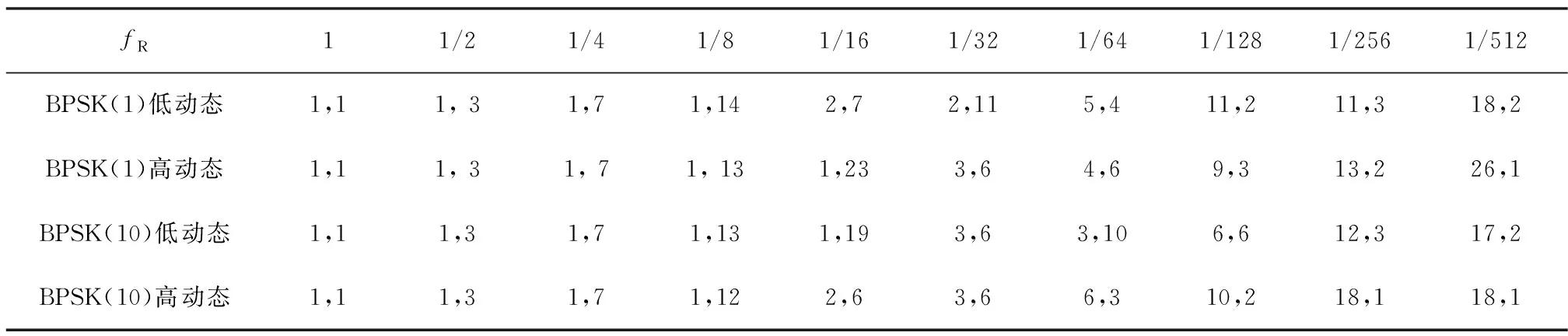
表5 輔助接收機不同頻率搜索范圍壓縮量下捕獲算法最優參數(Tcoh,Nncoh)

1)隨著偽碼相位壓縮量和頻率搜索范圍壓縮量的增加，最優捕獲算法的總信號處理時長在不同條件下均有一定程度的增長，即算法主要通過提升總信號處理時長來提高捕獲靈敏度。

2)相較于頻率搜索范圍壓縮，偽碼相位搜索范圍壓縮情況下的最優捕獲算法總信號處理時長提升量較小，僅提高至初始值的2倍，這與在分析過程中以頻率并行算法作為分析的基礎有關。

3)在頻率搜索范圍壓縮量達到初始值1/8的過程中，最優捕獲算法的非相干積分時長逐漸提高，隨著頻率搜索范圍壓縮量的進一步增加，最優捕獲算法的相干積分時長逐漸提高，若不考慮計算復雜度要求下的相干積分時長限制，最高達到26ms。這是由于在相干積分時長提高的同時，頻率搜索數量成比例增長，容易導致平均捕獲時間大幅度提升，因此將計算復雜度作為約束條件是有必要的。

4)相較于低偽碼碼率信號，高偽碼碼率信號最優捕獲算法的總信號處理時長更短，這是由于高偽碼碼率更容易受到偽碼多普勒損耗的影響，降低相關積累增益。

5 結論

本文通過對多個算法模型進行融合，在平均捕獲時間和捕獲算法復雜度約束下，分析了通過通信輔助壓縮信號偽碼相位搜索范圍以及頻率搜索范圍的情況下，采用優化捕獲算法可實現的捕獲靈敏度提升量。

基于并行捕獲算法，本文針對BPSK(1)和BPSK(10)在不同類型載體的典型動態條件下，給出了捕獲靈敏度提升量與偽碼相位搜索范圍以及頻率搜索范圍壓縮量之間的量化關系，并給出了不同條件下最優捕獲算法的算法參數。

根據分析可知，輔助接收機捕獲靈敏度提升量與捕獲概率、虛警概率指標關系較小，因此，通過本文方法得到的不同輔助條件下的最優捕獲算法具有通用性。接收機可預先進行優化設計并將最優算法進行存儲，根據運行過程中輔助條件下偽碼相位搜索范圍和多普勒頻率搜索范圍選擇相應的捕獲算法參數，從而取得最優的捕獲靈敏度效果。

本文通過上述捕獲靈敏度評估，明確了同等條件下輔助接收機捕獲靈敏度的提升量，可指導后續衛星導航增強系統建設的指標設計。