圓柱形扭簧簧圈橢圓度對應力及剛度的影響

姜旭濤，黃志輝，穆云飛

(西南交通大學 牽引動力國家重點實驗室，四川 成都 610031)

0 引言

某用于鋼琴踏板的圓柱螺旋扭轉彈簧(以下簡稱扭簧)，通過鋼琴踏板活動，在變載荷應力下工作50萬次后發生疲勞破壞，與設計要求的疲勞壽命N≥100萬次差異較大。因此，對扭簧實物進行檢查后發現扭簧簧圈制成了橢圓形，而非標準圓形。為探究扭簧簧圈橢圓度對扭簧部分力學性能的影響，本文就簧圈橢圓度對扭簧所受應力及剛度的影響進行研究與分析。

1 標準簧圈扭簧部分力學性能理論計算

1.1 扭簧研究模型介紹

該扭簧順旋向扭轉，使用SWP-B琴鋼絲材料，總圈數n=5.21，初始夾角φ0=104.4°，材料直徑d=3.8mm，內徑D1=16mm，固定側扭臂l1=66mm，施力側扭臂l2=45mm，自由高度H=33.29mm，安裝轉矩T1=4599.20N·mm，工作轉矩T2=6 713.87N·mm。

在CATIA中建立扭簧三維模型時，通過高度h=H-d=33.29-3.8=29.49mm以及轉數n=5.21來定義螺旋曲線；將螺旋曲線與兩扭臂l1、l2接合并將其作為中心曲線，將d=3.8mm的圓作為輪廓，定義肋，得到標準簧圈扭簧的三維模型如圖1所示。

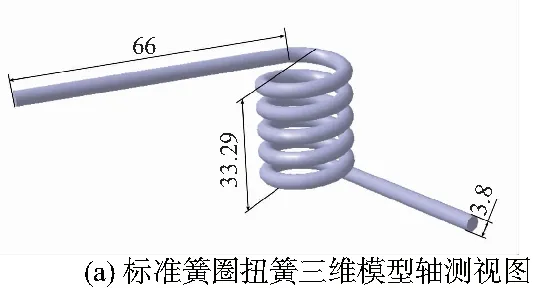
圖1 標準簧圈扭簧三維模型

1.2 扭簧彎曲應力計算

根據GB/T 23935—2009《圓柱螺旋彈簧設計計算》[1]，該扭簧所受彎曲應力的計算公式為

(1)

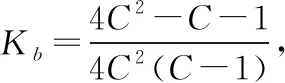
將安裝轉矩T1與工作轉矩T2分別代入公式(1)中，得：

該扭簧所受最小彎曲應力

所受最大彎曲應力

1.3 扭簧疲勞極限分析

扭簧在應力循環中的循環特征的計算公式為

(2)

則該扭簧的循環特征

查得當材料直徑d=3.8mm時，SWP-B琴鋼絲的抗拉強度Rm為1810～1960MPa[2]，取Rm=1810MPa，則該扭簧的上限應力系數

根據扭轉彈簧疲勞極限圖(圖2)判定規則：若循環特征γ與上限應力系數Q的交點在圖中應力循環10n下方，說明該扭簧的疲勞強度N>10n次。

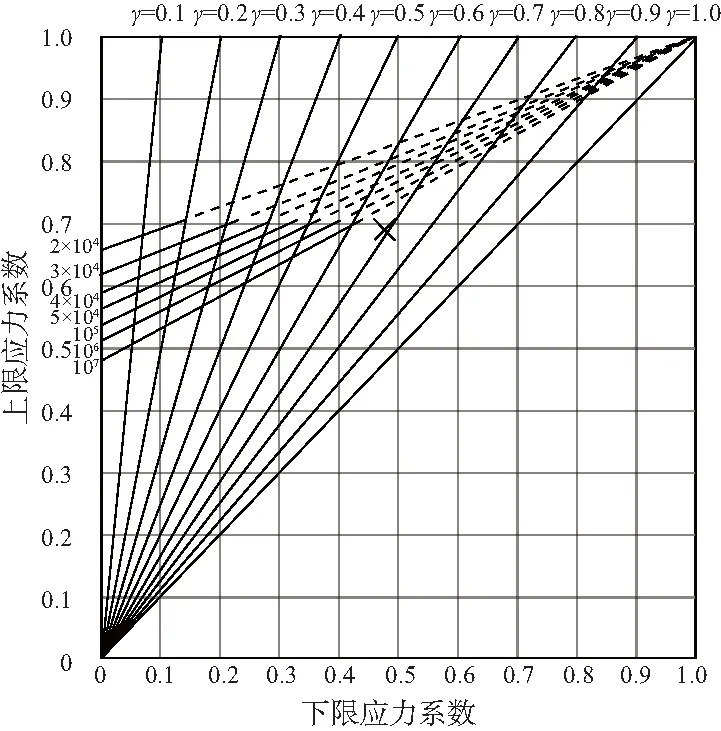
圖2 扭轉彈簧疲勞極限圖

在圖2中，該扭簧循環特征γ與上限應力系數Q的交點在圖中107下方，理論上疲勞壽命N>107次[3]。

2 標準簧圈扭簧有限元計算

本文通過在CATIA建立扭簧三維模型，將扭簧模型以stp格式導入HyperMesh進行網格劃分、賦予材料屬性、設置單元屬性、建立接觸、施加載荷及邊界條件，然后輸出cdb模型，將其導入ANSYS進行計算[4-5]。

2.1 扭簧有限元模型建立

根據扭簧實際工作情況，將扭簧三維模型導入HyperMesh后，建立與扭簧接觸處間隙為0的銷軸。

兩者都采用SWP-B琴鋼絲材料，SWP-B琴鋼絲的材料屬性如表1所示。

表1 SWP-B琴鋼絲材料屬性

根據扭簧實際工作情況，扭簧與銷軸之間存在接觸，所以需要對接觸部分進行非線性接觸設置，設置銷軸表面為目標面，扭簧表面為接觸面 。

根據扭簧實際工作情況，l1=66mm端為固定側扭臂，l2=45mm端為施力側扭臂。在扭簧工作時，固定側扭臂只在軸向發生位移，而施力側扭臂由于受轉矩T的作用，只在軸向和轉矩方向發生位移，銷軸在扭簧工作期間為固定的。對于固定側扭臂，需在扭臂端面建立一空間直角坐標系，然后將固定側扭臂上需要約束的節點分配給該局部坐標系，約束固定側扭臂節點Ux和Uy自由度；對于施力側扭臂，在全局坐標系中約束其Uz自由度；對于銷軸，在全局坐標系中約束其上、下端面的Ux、Uy和Uz自由度。

在有限元模型中，對扭簧轉矩的施加要轉化成力乘以力臂，公式為

T=FR

(3)

式中：F為施加在扭臂的力，N；R為力臂，mm[6]。

扭簧的工作轉矩T2=6 713.87N·mm，取力臂R1=33.75mm，由公式(3)得施加在扭臂的力為

采用mass質量單元與rbe3剛性單元，將扭簧施力側扭臂的受力節點耦合為一個受力節點。由于無法對耦合后的節點直接施加垂直于扭臂的載荷，所以需要在扭簧銷軸的中心位置建立空間柱坐標系，然后將力F沿柱坐標系分解為F1=50.72N，-F2=192.35N，將其施加在耦合的受力節點上。

HyperMesh處理后的標準簧圈扭簧有限元模型如圖3所示。

圖3 標準簧圈扭簧有限元模型

2.2 扭簧有限元模型計算結果

將HyperMesh處理的有限元模型導入ANSYS進行求解。扭簧Von-Mises等效應力云圖如圖4所示。

圖4 標準簧圈扭簧Von-Mises等效應力云圖

由有限元計算結果可知，扭簧所受最大應力為1272.69MPa，位于扭簧內圈扭轉處。經測量，扭簧扭轉變形角φ1=56°。根據現代機械設計手冊[7]，扭轉剛度與扭轉角的關系式為

(4)

將扭轉變形角代入公式(4)可得有限元計算的扭轉剛度為

3 橢圓簧圈扭簧有限元計算

在彈簧成型過程中，由于工裝及加工的原因，使得簧圈成了橢圓，且每個彈簧的橢圓度都不一致。本文采取等距取樣的原則，以0.5mm為抽樣距離進行簧圈橢圓度的取值，首先選取簧圈橢圓度e為0.5mm、1.0mm、1.5mm的扭簧并對其進行有限元計算。將有限元計算結果進行分析擬合，得到簧圈橢圓度與扭簧所受最大應力呈線性關系的結論。為了驗證結論的準確性，選取簧圈橢圓度e為3.0mm的扭簧進行有限元計算。

橢圓簧圈扭簧三維模型如圖5所示。

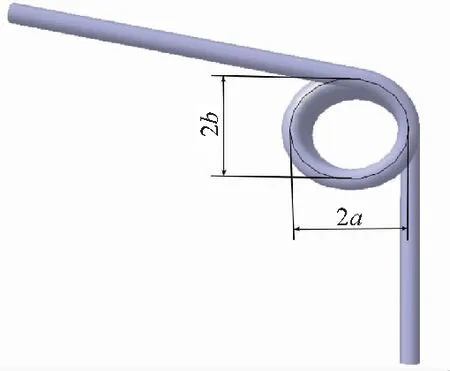
圖5 橢圓簧圈扭簧三維模型

3.1 橢圓簧圈扭簧三維模型建立

在橢圓中，橢圓度與橢圓長、短軸的關系式為

e=2a-2b

(5)

式中：e為橢圓度，mm；a為橢圓長半軸，mm；b為橢圓短半軸，mm。

橢圓周長公式為

C1=2πb+4(a-b)

(6)

構造橢圓簧圈扭簧時，需保證橢圓簧圈與標準簧圈周長相同，即

2πb+4(a-b)=πD

(7)

將4組橢圓度e分別代入公式(5)中，并與公式(7)聯立，得到各組橢圓簧圈的參數如表2所示。

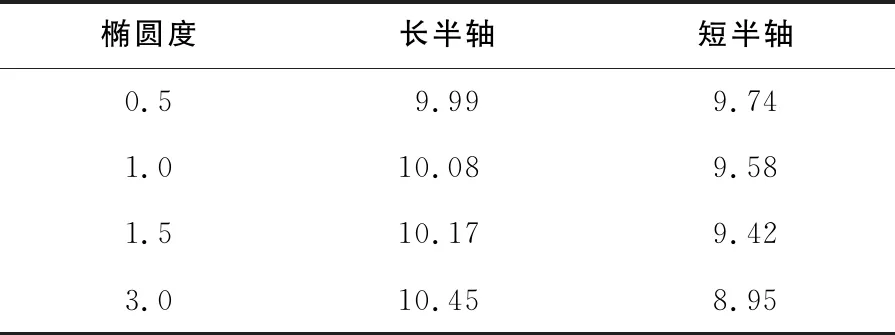
表2 橢圓簧圈參數 單位：mm

利用計算所得參數在CATIA中分別構造對應橢圓度的橢圓簧圈扭簧。

3.2 橢圓簧圈扭簧有限元模型建立

采用與2.2中標準簧圈扭簧有限元模型相同的方式分別對各組橢圓簧圈扭簧進行網格劃分，單元、材料、接觸設置及約束和載荷的施加。

3.3 橢圓簧圈扭簧有限元模型計算結果

將HyperMesh處理的有限元模型導入ANSYS進行求解。各組橢圓簧圈扭簧Von-Mises等效應力云圖分別如圖6-圖9所示。

圖6 0.5mm橢圓度扭簧Von-Mises等效應力云圖

圖7 1.0mm橢圓度扭簧Von-Mises等效應力云圖

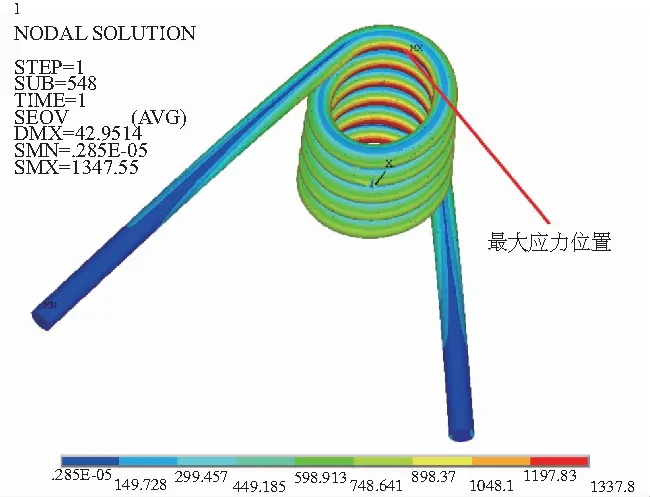
圖8 1.5mm橢圓度扭簧Von-Mises等效應力云圖

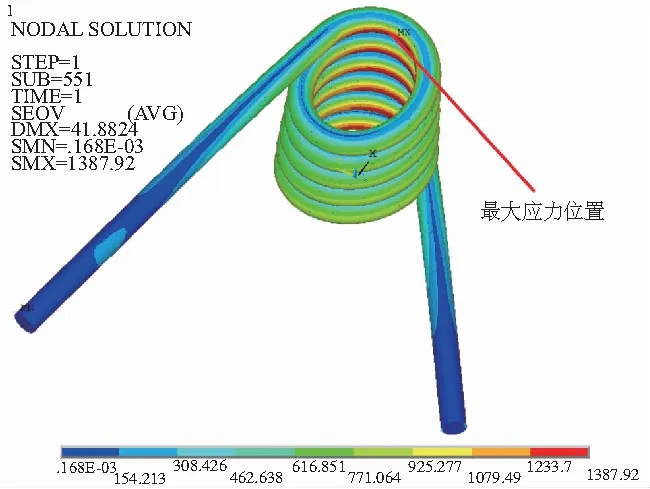
圖9 3.0mm橢圓度扭簧Von-Mises等效應力云圖

整理得各組扭簧有限元計算結果如表3所示。

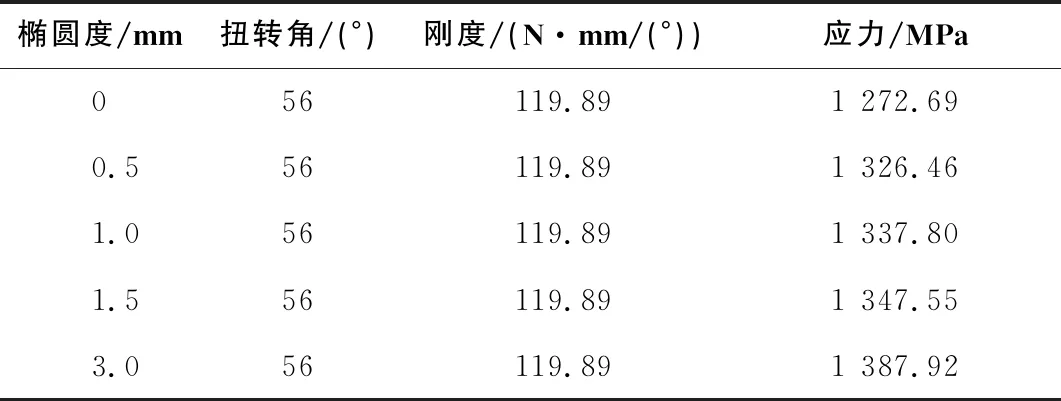
表3 各組扭簧有限元計算結果

4 有限元計算結果分析

4.1 簧圈橢圓度對剛度的影響

由表3可知，扭簧剛度不隨簧圈橢圓度的變化而變化，即簧圈橢圓度對扭簧剛度沒有影響。

4.2 簧圈橢圓度對應力的影響

以簧圈橢圓度e為橫軸，以應力σ為縱軸，將表3中各組橢圓度所對應的應力值進行擬合，得到擬合曲線σ=24.72e+1312.85(e>0)，如圖10所示。

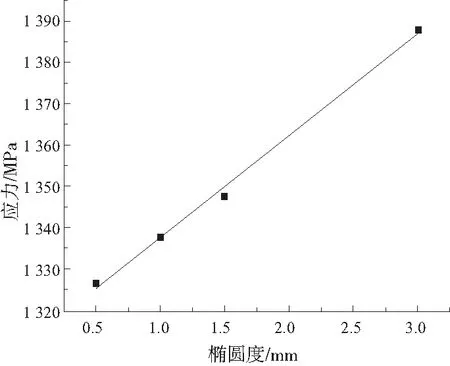
圖10 簧圈橢圓度與所受最大應力關系擬合曲線

5 結語

1)扭簧簧圈橢圓度對扭簧的剛度沒有影響。

2)扭簧所受最大應力隨扭簧簧圈橢圓度的增大而增大，且兩者呈線性關系；在本文選取的模型中，扭簧橢圓度與所受最大應力的線性關系式為σ=24.72e+1312.85(e>0)。