一種中壓絕緣大功率中頻變壓器的優化設計方法

王佳寧 鄒 強 胡嘉汶 裴 偉 趙玉順

一種中壓絕緣大功率中頻變壓器的優化設計方法

王佳寧 鄒 強 胡嘉汶 裴 偉 趙玉順

（合肥工業大學電氣與自動化工程學院 合肥 230009）

應用于光伏并網系統的中壓絕緣大功率中頻變壓器（MFT）不僅要求其高低壓側繞組之間需要滿足較大的絕緣間距，而且其內部也需要澆注隔熱的絕緣材料。然而，這會導致MFT出現電磁干擾現象嚴重、散熱困難等問題。針對這些問題，該文提出一種全面考慮鐵心尺寸、繞組線徑和繞組排布結構的MFT優化設計方法。該方法通過面積乘積（AP）法確定鐵心體積，再通過自由變量掃描對MFT進行損耗最小化設計。基于有限元仿真軟件，驗證了該優化設計方法可使變壓器漏電感減小及周圍的電磁干擾區域縮小。最后，通過該優化設計方法設計一臺200kW/ 30kHz的MFT，并制作了樣機。通過理論和實驗的對比，驗證了優化設計方法的有效性和準確性。

大功率中頻變壓器 絕緣 面積乘積法 損耗建模 優化設計 電磁干擾 有限元仿真

0 引言

由于光伏發電逐漸形成大規模集中開發和中高壓接入電網的局面，對電氣設備的體積和質量也有一定的限制[1-4]，使得中壓大功率電力電子變壓器受到了廣泛關注。相比于傳統低頻變壓器，大功率電力電子變壓器中工作頻率大多在1～50kHz的中頻范圍，因此具有更小的體積和質量[5-9]。受目前開關器件耐壓水平的限制，電力電子變壓器的隔離和升壓一般通過多個模塊化大功率DC-DC變換器級聯實現[10]，在低壓側并聯，高壓側串聯。

中頻變壓器（Medium Frequency Transformer, MFT）作為DC-DC變換器的核心器件之一，由于自身結構的緊湊性，以及中頻和中壓的結合，使其設計具有較大的挑戰性。首先，頻率的升高雖然可以實現更高的功率密度，但也會導致MFT的繞組損耗和鐵心損耗增大[11-13]，從而增大了散熱難度且限制了效率的提高。其次，中壓帶來的絕緣需求也會產生兩個問題：①高壓側繞組和低壓側繞組之間需要保持較大的絕緣間距，這使得MFT會產生更多的高頻漏磁，從而對DC-DC變換器中的其他電路產生電磁干擾[14]，影響穩定性；②MFT內部澆注隔熱的絕緣材料，這導致變壓器的散熱難度進一步增大。所以在設計MFT時，不僅需要滿足功率密度的需求，而且也需要最小化損耗來盡可能地降低溫升，同時也要兼顧MFT電磁干擾的影響。

一般選擇低損耗密度的鐵心材料（如鐵氧體、納米晶）可以降低鐵心損耗。通過降低繞組交流電阻和直流電阻的比值（稱為交流電阻因子），可以降低繞組的交流損耗[15]。交流電阻因子主要受趨膚效應和鄰近效應的影響[16]。繞組選擇利茲線或者銅箔可以有效地降低趨膚效應的影響[17]；改變繞組排布（繞組層數）和鐵心尺寸可以降低繞組周圍的磁場強度，從而降低鄰近效應的影響。故為了最小化MFT損耗，需要考慮鐵心材料、鐵心尺寸、繞組材料、繞組尺寸和繞組排布等關鍵參數。

由于鐵心磁導率不是無窮大，故實際MFT會存在漏磁通。一方面，漏磁通形成的漏感可被LLC諧振變換器、隔離型DC-DC變換器等用作能量傳遞元件[18-20]。LLC諧振變換器因具有全負載范圍內實現軟開關的特性而被廣泛使用。LLC諧振變換器使用漏感作為諧振電感時，漏感越小使得LLC諧振變換器的諧振電容電壓應力越小；另一方面，因為模塊化DC-DC變換器的功率密度較高，MFT的高頻漏磁通產生的電磁干擾可能會在周圍電路上產生感應電壓和電流，同時產生額外損耗，從而降低電路穩定性和變換器的效率。因此，在設計MFT時應盡量減少漏磁通或對其進行屏蔽。

MFT的優化設計方法已有較多研究。面積乘積（Area Product, AP）法作為常用的MFT設計方法，能夠快速地通過解析公式對MFT進行設計[21-22]。但因為AP法對鐵心的設計多是根據其計算得到的面積乘積的值選擇合適的商用鐵心，這使得MFT的損耗并不一定能達到最小。文獻[23]介紹了通過遺傳算法來兼顧損耗和漏感的MFT多目標優化設計，并設計了一臺3.52kW/20kHz的MFT。但自由變量僅僅考慮了繞組的排布參數，這也會導致損耗不能達到最小。文獻[24]介紹了在考慮溫度、磁通密度、介電強度以及外部尺寸的限制條件下，通過自由參數掃描選出以功率密度和損耗為設計目標的最優方案，并設計了一臺166kW/20kHz的MFT。然而，繞組尺寸從標準尺寸列表中選擇，同樣會限制損耗的最小化設計。文獻[25]介紹了通過自由參數掃描，找到滿足效率、隔離、散熱和漏感要求的最高功率密度MFT，設計了一臺1MW/5kHz的具有較高絕緣性能的MFT。但沒有考慮損耗的最小化設計以及絕緣帶來的電磁干擾問題。文獻[26]介紹了通過自由參數掃描法選出兼顧損耗、漏感和質量的MFT最優設計方案，設計了一臺300kW/5kHz的高絕緣性能的MFT，同樣也沒有對電磁干擾問題進行研究。

為了實現中壓絕緣大功率MFT的損耗最小化設計，同時兼顧電磁干擾問題。本文提出了一種全面考慮鐵心尺寸、繞組線徑和繞組排布結構的MFT優化設計方法。該方法使用AP法設計鐵心體積，建立鐵心和繞組損耗模型并通過自由參數掃描使MFT損耗達到最小。對所述的MFT損耗最小化方法進一步分析，證明其也會帶來漏感的降低以及電磁干擾區域的縮小。隨后，基于Ansys Maxwell有限元仿真軟件，對上述分析的正確性進行驗證。最后，根據提出的MFT優化設計方法設計并制作了一臺35kV絕緣、200kW/30kHz的MFT樣機，對所提優化設計方法的有效性和準確性進行驗證。

1 MFT的建模

1.1 MFT的結構

本文研究的MFT應用于35kV光伏并網系統DC-DC變換器中，變換器為LLC諧振變換器，MFT結構和LLC諧振變換器電路拓撲分別如圖1、圖2所示。鐵心選用鐵氧體材料，由多個磁塊拼接而成，氣隙設置在鐵心的拼接處。繞組由一個一次繞組（低壓側）和兩個相同的二次繞組（高壓側）組成。一次和二次繞組每匝均使用4根相同的導線并聯。繞組采用雙柱繞制結構，一次與二次繞組均分成相同的兩部分，分別繞制在鐵心的A柱和B柱上。為了滿足高壓繞組與低壓繞組、鐵心之間35kV的絕緣要求，需要留出足夠的絕緣間距用來填充絕緣材料。

圖1 MFT的結構

圖2 LLC諧振變換器電路拓撲

圖1中，、分別為鐵心窗口的寬度和高度；、分別為鐵心柱截面的寬度和厚度；g為氣隙的厚度；p、s分別為一次和二次繞組的層數；lp、ls分別為一次和二次繞組每層的匝數；p、s分別為一次和二次繞組的每根導線外直徑（包含絕緣層）；cph、cpv分別為一次繞組到鐵心柱和鐵軛的距離；wp和ws分別為一次和二次繞組的高度；wp和ws分別為一次和二次繞組的寬度；ps為一次和二次繞組間的絕緣間距；cs為二次繞組和鐵心的絕緣間距。圖2中，in為LLC諧振變換器的輸入電壓；o為LLC諧振變換器的輸出電壓；r為諧振電容；r為諧振電感，由外接電感s和MFT的漏感k組成；m為勵磁電感；n為r和m上的電壓之和；s為變換器的輸出電壓。

基于應用場合相關電氣參數，35kV絕緣MFT的設計要求見表1。

表1 35kV MFT的絕緣設計要求

Tab.1 Design requirements of 35kV insulated MFT

1.2 MFT體積的設計

首先對MFT的鐵心體積進行設計。根據文獻[21]可知，MFT的鐵心體積和值之間存在的約束關系為

式中，c為鐵心體積；c為一個常系數，與鐵心類型有關。可以看出，在鐵心材料確定后，保持的值不變，即可保證鐵心體積不變。

為了能夠滿足溫升限制，本文引用AP法中的面積乘積的計算公式設計鐵心體積[22]，如式（2）所示。其中，初始的最大磁通密度m根據鐵心類型與其損耗曲線選擇合適的值。

在確定鐵心體積之后，繼續對鐵心損耗和繞組損耗進行建模，并分析MFT關鍵的自由變量。

1.3 鐵心損耗建模

在電力電子變壓器中，電壓波形大多為矩形波。為了保證模型的精度，本文引用改進的通用斯坦梅茲公式（Improved Generalized Steinmetz Equation, IGSE）[27]，該公式可較為準確地計算任意非正弦激勵下的鐵心損耗，即

其中

式中，、、為常系數，可以從鐵心的損耗曲線或數據手冊中得到；為電壓周期；d()/d為磁通密度隨時間的變化率；D為的峰峰值，本文中，D=2m。

根據法拉第電磁感應定律，m可以表示為

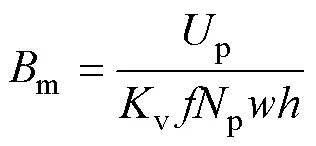
式中，p為一次繞組的匝數。因鐵心體積不變可知，鐵心損耗主要由p、和決定。

1.4 繞組損耗建模

在中高頻下，繞組因鄰近效應和趨膚效應而產生交流損耗，可采用Dowell模型對交流損耗進行計算[15]。

首先計算繞組的直流電阻，MFT的繞組選用利茲線制作，由于利茲線內部結構導致其截面的實際導流面積和整體面積有較大的差異，二者分別影響繞組損耗模型的精度與其在鐵心窗口中的排布。所以為了同時滿足繞組損耗建模精度和繞組在鐵心窗口中的精確排布，建立參數：利茲線可用面積在整體面積中的占比為w，計算式如式（6）所示。本文根據開關頻率，選擇單股利茲線徑為s=0.15mm，然后根據利茲線實際制作工藝，確定w-avg（即不同利茲線股數對應的w平均值）為0.55。

式中，為利茲線股數；為利茲線截面直徑。

由于本文中采用的繞組骨架結構為橢圓形，為了方便繞組的平均匝長建模且滿足精度，本文將橢圓形結構簡化為矩形結構，繞組匝長的簡化模型如圖3所示。

圖3 繞組匝長的簡化模型

針對特定的磁心，首先測量其相應的橢圓結構實際平均匝長。隨后保持相同的絕緣距離，對如圖3b所示的矩形結構進行理論平均匝長建模，與橢圓結構實際平均匝長作比得到平均匝長系數，基于此就可以建立橢圓形骨架的平均匝長模型。一次和二次繞組的平均匝長模型分別為

式中，為矩形結構的平均匝長轉化為橢圓形結構的平均匝長系數；p、s分別為一次、二次繞組的平均匝長。

由于兩個二次繞組完全相同，故為了方便二次繞組損耗建模，假設A、B鐵心柱上的兩個二次繞組串聯，等效為一個繞組。等效二次繞組的每層匝數為2ls，層數不變為s，總繞組匝數為2s。

根據圖1的MFT結構，一次與等效二次繞組的直流電阻dcp和dcs分別為

式中，w為導線的電阻率。

將直流電阻乘以Dowell模型求得的交流電阻因子Ri，即可得到繞組交流電阻[28-29]。在本文研究的MFT結構中，一次繞組需遠離氣隙以減小氣隙效應帶來的損耗，故上下端和鐵軛之間需留出一定的間距；二次繞組因絕緣要求高，上下端和鐵軛之間也需留出較大的絕緣間距。這導致一次、二次繞組實際的孔隙率都較低，使得Dowell模型的計算誤差變大。為了提高該結構下的交流電阻計算精度，本文引入文獻[30]的校正因子Ri，該校正因子主要是通過校正繞組高度的方式來校正，表達式為

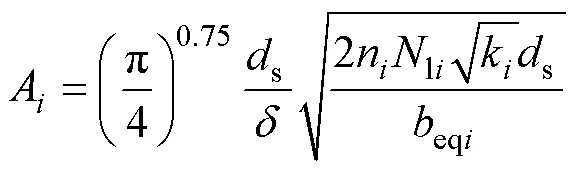
式中，Ri為交流電阻和直流電阻的比值；為標準化后的單股線徑和趨膚深度的比值；為趨膚深度；li為每層繞組的匝數（等效二次繞組按2ls計算）；為單根利茲線股數；eqi為修正后的繞組高度。

對于任意電流波形的繞組交流損耗計算，首先需要將電流進行傅里葉分解，然后將電流直流分量下的繞組損耗和各次諧波下的繞組交流損耗相加，本文所研究MFT應用于LLC諧振變換器，其中工作電流為正弦波，因此其繞組損耗可只考慮基波下的交流損耗，得到一次繞組損耗windingp與二次繞組損耗windings表達式分別為

2 MFT的優化設計

在第1節對鐵心體積、鐵心損耗和繞組損耗模型的分析基礎上，本節對參數如表1所示的MFT進行優化設計。

根據損耗模型的分析，可知鐵心損耗與繞組損耗可由以下8個變量結合求得，因此將其作為優化關鍵變量，分別是關于鐵心尺寸的3個變量：鐵心柱截面兩個尺寸、和鐵心窗口高度；關于繞組的5個變量：一次繞組匝數p，一次、二次繞組的利茲線的直徑p和s，一次、二次繞組的層數p和s。其中，、、p既影響鐵心損耗也影響繞組損耗，、p、s、p、s只影響繞組損耗。

MFT的優化設計流程如圖4所示。整個優化設計流程分為三大步。

圖4 MFT的優化設計方法流程

（1）先根據設計要求確定鐵心材料、繞組材料和絕緣間距等相關固定參數，然后根據式（1）確定MFT的值。其中，本文選用的鐵心材料為錳鋅鐵氧體材料。

（2）首先確定優化變量的設計范圍，然后基于Matlab軟件，掃描給定變量取值范圍內的所有設計的總損耗值tot，總損耗tot為

再從所有設計點中找出滿足約束條件的設計點，約束條件包括鐵心值的限制和m的限制：m不得超過鐵心柱中最大飽和磁通密度sat的50%；窗口預留絕緣距離與制作工藝誤差裕度的限制，窗口需要給二次繞組預留2cs的絕緣距離和不小于ps的工藝誤差裕度，為一次繞組預留不小于ps的工藝誤差裕度；窗口長度裕值，除繞組所占距離之外，窗口還需預留15mm及以上，具體為

式中，sat為鐵心柱中最大飽和磁通密度。隨后對比得出損耗最小值。

（3）首先輸出總損耗最小對應的最優變量解集，然后計算變壓器剩余的結構參數，最后確定最優設計方案。

優化變量的取值范圍首先針對p進行選取，選取一個較寬的取值范圍，以獲得較大的數據集。根據p取值范圍與m的取值，劃定鐵心柱截面的取值范圍，即與的取值范圍。p、s的取值范圍按載流量1～8A/mm2選取，同時基于p范圍與p和s范圍確定窗口高度的范圍。

隨后，本文進一步分析了變量p、s對損耗的影響程度以定性分析優化設計方法后MFT特點。在分析過程中，基于損耗模型與約束條件，分別改變p與s，并將其余7個變量固定，計算損耗（包括鐵心損耗、繞組損耗和總損耗），觀察變化趨勢；重復上述步驟。因樣本量繁雜，趨勢接近，難以全部展示，故選擇一組具有代表性的數據進行展示，不同優化變量和MFT損耗的關系如圖5所示。圖中，主要分析滿足約束條件的點（灰色區域覆蓋），故不滿足約束條件的點對應損耗被設置為0。變量p、s只能取整數。

從圖5中可以看出，p從1層增大到2層，繞組損耗增大了24.1%；s從2層增大到3層，繞組損耗增大了36.4%。這是因為p和s的增大會較大程度地加重鄰近效應，從而導致繞組交流損耗較大幅地增加，且隨著繞組層數的增大，繞組損耗的增加幅度越大。故在優化設計MFT時會盡可能減少繞組層數。層數的減少意味著每層繞組匝數的上升，因此會提高窗口高度，并且由于值恒定的限制，窗口長度具有減小趨勢。

圖5 不同優化變量和MFT損耗的關系

因此，本文的損耗最小化設計方案中繞組具有較小的n，鐵心具有較高的窗口，呈現“瘦高型”。優化變量的取值范圍見表2，鐵心的厚度方向采用多個截面為方形的鐵氧體磁塊進行拼接，為拼接的數量。

表2 優化變量取值范圍

Tab.2 Range of optimization variables

根據圖4的優化設計流程，選擇優化設計中最小MFT總損耗的設計結果方案，見表3。MFT為MFT的體積；MFT為MFT的效率；為MFT的功率密度。

表3 MFT的優化設計結果

Tab.3 Optimal design results of MFT

（續）

3 MFT的漏感和電磁干擾

本節主要研究了優化設計的MFT漏感和電磁干擾問題。漏感和電磁干擾主要由變壓器的漏磁能量所致。漏磁能量一般由兩部分組成[6]：一部分儲存在繞組導體中，這部分漏磁大小會影響繞組的鄰近效應強度，進而影響繞組的交流損耗，穿過導體的漏磁磁場強度越大，繞組交流損耗越大；另一部分儲存在絕緣區域（包括空氣），鐵心窗口截面及繞組中的磁動勢分布如圖6所示。由安培環路定律以及圖6可知，變壓器的繞組層數越大，最外層繞組的磁動勢（Magnetomotive Force, MMF）越大，進而導致穿過該層和該層以外的繞組的漏磁磁場強度越大；鐵心窗口高度越小則減小了窗口中磁通的磁路長度，導致穿過繞組導體和一次、二次繞組之間絕緣區域的漏磁磁場強度更大。故可以得知，增大和減小會帶來穿過繞組導體和一次、二次繞組之間絕緣區域的漏磁磁場強度減小，進而帶來漏感和變壓器周圍電磁干擾強度的降低。通過第2節分析可知，MFT的優化設計會帶來的增大和的減小，并減小交流損耗，因此也可預見，MFT的優化設計方法不僅會降低交流損耗，也會使穿過繞組的漏磁磁場強度減小，從而減小漏感與電磁干擾。

為了驗證本文優化設計的MFT在損耗達到最小化的同時也帶來了漏感和電磁干擾現象的改善，本文引用文獻[18]中的AP法對MFT進行設計，然后將AP法設計和本文所提優化方法設計的MFT在漏感和電磁干擾方面進行對比。

圖6 鐵心窗口截面及繞組中的磁動勢分布

表4為AP法設計的MFT參數，對比表4可以看出，本文的優化設計方法設計的MFT在繞組損耗上有較大程度的降低。

表4 AP法設計的MFT結構及電氣參數

Tab.4 MFT structure and electrical parameters designed by APmethod

利用Ansys Maxwell有限元仿真軟件對表3和表4的MFT勵磁電感m和漏感k進行仿真對比，結果見表5。

表5 AP法和本文優化方法設計的MFT的m和k仿真

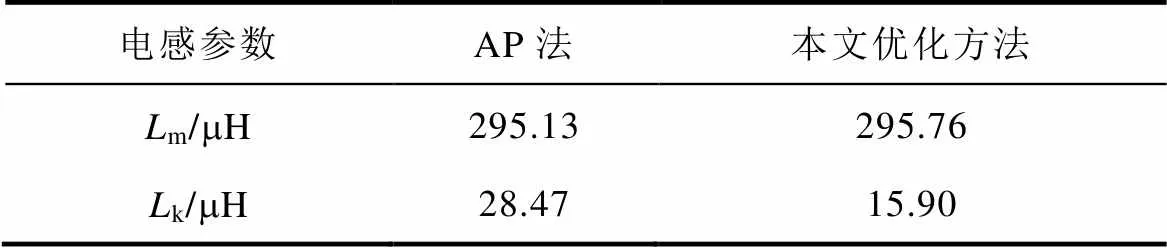
Tab.5 The simulated values of Lm and Lk of MFT designed by AP method and the optimial method in this paper

從表5中可以看出，本文所提優化設計方法設計的MFT漏感比AP法的設計小了將近一半，證明了上述理論分析的正確性。同時兩臺變壓器m的仿真值基本相同，因為氣隙長度和繞組匝數相同。

然后對漏磁引起的電磁干擾現象進行研究，因漏磁場的分布難以用數學模型準確計算得到，為此也采用有限元仿真方法進行研究，通過觀察變壓器周圍的漏磁場磁感應強度和磁場強度云圖可較為直觀地觀察并對比電磁干擾的強度，但不易定量分析。為準確量化對比電磁干擾的強度，采用如下方法：通過在MFT外側放置鋁板，改變鋁板到MFT二次繞組的距離，觀察鋁板因漏磁場帶來的渦流效應導致的損耗情況，漏磁場越強，則電磁干擾越強，渦流效應越明顯，帶來的損耗也越大，從而側面定量反映MFT在此處的電磁干擾強弱。圖7為在Ansys Maxwell軟件中描述兩臺MFT外側電磁干擾現象的簡化仿真模型。

圖7 MFT周圍電磁干擾現象研究的簡化模型

圖8展示了當=50mm時，兩臺MFT外側漏磁場磁感應強度的分布，選用鋁板為參照物。可以直觀地看出，基于本文所提優化方法設計的MFT，鋁板周圍的更小。從而說明本文所提優化方法設計的MFT對外側的電磁干擾影響更小一些。

圖8 d=50mm時，MFT周圍B的分布

圖9展示了兩臺MFT外側的鋁板損耗（兩個MFT外側的鋁板損耗以AP法設計的MFT外側鋁板長度為基準，參照實際厚度，在保持相同電阻的情況下，進行了數據折算），以定量分析MFT對外電磁干擾的影響，隨著鋁板位置變化而變化的曲線。從圖中可以看出，隨著的增大，鋁板損耗越小，同時損耗的變化率也越來越小。當為5～25mm的時候，基于AP法設計的MFT外側鋁板損耗可達優化設計后MFT外側鋁板損耗6～10倍，可知這段區域內基于AP法設計的MFT對外電磁干擾強度遠超優化設計后的MFT對外電磁干擾強度。當＞120mm時，基于AP法設計的MFT外側鋁板損耗接近0且損耗變化率趨于平穩，說明鋁板在該范圍內受電磁干擾的影響較小，可判定該范圍屬于電磁干擾較弱區域；反之，在0＜＜120mm范圍內屬于電磁干擾較強區域。同理，基于本文優化方法設計的MFT，在0＜＜80mm范圍內屬于電磁干擾較強區域。通過對比說明了相對于AP法的設計，本文所提優化方法設計的MFT的外側電磁干擾區域也得到了較大程度的改善。

圖9 兩臺MFT的電磁干擾強弱區域分布對比

4 實驗驗證

為了驗證本文所提優化設計方法的準確性，根據表3的設計結果，設計了一臺200kW/30kHz的MFT樣機，如圖10所示，該樣機預留了絕緣間距，暫未填充絕緣材料。其LLC諧振變換器實驗平臺如圖11所示。

圖10 優化設計的MFT樣機

4.1 電氣參數的測量

首先對變壓器樣機的m和k大小進行測量。通過阻抗分析儀WK6500B對MFT樣機的m和k的測試結果見表6，與表5對比可得，測量值和仿真值結果近似。誤差產生的原因為變壓器樣機的氣隙尺寸與仿真中的設定值不能保證完全一致，導致勵磁電感無法完全一致；因實際利茲線與變壓器骨架帶來的偏差，實際的一次、二次繞組間的絕緣間距與仿真中的設定值不能保證完全一致，導致漏感的偏離，但該誤差的偏差在可接受范圍內。

圖11 LLC諧振變換器實驗平臺

表6m和k的測試值

Tab.6 Tested values of Lm and Lk

4.2 效率和溫升的測量

為了驗證本文優化設計的MFT的工作性能，本文從輕載到滿載分別測試了9個功率點的工作狀態。MFT的工作環境為：測試場地為密閉室內，室溫約為28℃且室內無風，MFT的一端放置三聯裝風扇進行風冷散熱，在風扇對側放置熱成像儀進行溫升測量，如圖11所示。LLC諧振變換器的輸入電壓恒定為1 300V。圖12展示了100kW和200kW下的諧振電流p、諧振電感兩端電壓加上勵磁電感兩端電壓之和n的實驗波形。從p的正弦波形中可以得出，LLC諧振變換器工作在諧振點附近。

使用功率分析儀YOKOGAWA WT3000E分別對LLC諧振變換器中9個功率點的效率進行了測量。為了驗證優化設計方法的準確性，本文根據實際電壓和電流值對各個功率點下的效率進行了理論計算。

圖12 Ip和Un的實驗波形

理論計算主要考慮了逆變側開關管的通態損耗和關斷損耗、諧振電容的損耗、MFT總損耗、外接諧振電感損耗和整流二極管通態損耗。

其中，開關管的通態損耗為

式中，ds-rms為流過開關管的電流有效值；dson為開關管的通態電阻。

開關管的關斷損耗為

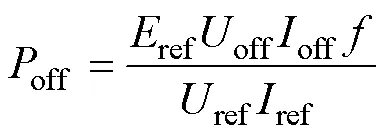
式中，ref、ref和ref分別為開關管Datasheet中給的參考關斷電壓、關斷電流和關斷時損失的能量；off和off分別為實際的關斷電壓和關斷電流。

根據電容的等效串聯電阻（Equivalent Series Resistance, ESR），諧振電容的損耗為

式中，Req為電容的等效串聯電阻。

整流二極管的通態損耗為

式中，dio-rms為流過二極管的電流有效值；F為二極管的通態壓降。外接電感的損耗建模方法與MFT一致。損耗計算中電壓電流參數均由實驗測得。

LLC諧振變換器效率的實測值和理論值的對比如圖13所示，可以看出，效率的實測值和理論值近似，在測試過程中，因主功率電路結構設計問題，開關管和二極管的殼溫極難測量。因而在開關管和二極管通態損耗中，dson和F采用典型值計算，實際中dson和F則具有正溫度變換特性，產生些許誤差，因此理論效率變換斜率稍小于實測效率，但誤差在可接受范圍內。實測值和理論值相當接近，證明了MFT理論模型的準確性。其中，最高實測效率點達到99.18%，滿載時的實測效率為98.59%。當滿載（200kW）時，LLC諧振變換器各部分的損耗分布理論值對比如圖14所示，可以看出，損耗主要集中在逆變側開關管的通態損耗和整流二極管的通態損耗。

圖13 LLC諧振變換器的效率實測值和理論值對比

圖14 Pin=200kW時，LLC諧振變換器的主要損耗分布

損耗最小化設計帶來直觀優點是較低的溫升。本文使用FLIR熱成像儀對滿載（200kW）下的MFT進行了溫升測量。在此條件下，工作了40min后溫度基本穩定，熱成像結果如圖15所示。由于外側的二次繞組受風冷散熱影響較大，故測得二次繞組溫升較低；而內側的一次繞組風扇難以吹到，同時熱成像位置在風扇對側，故測得一次繞組溫升較高。目前，整個MFT的最高溫為79.6℃，最大溫升為51℃左右，為后續考慮絕緣材料的MFT溫升裕留了足夠大的空間。

圖15 Pin=200kW時，MFT的熱成像

5 結論

本文討論了AP法設計鐵心體積的解析模型以及鐵心損耗和繞組損耗的解析模型，進一步討論了繞組層數和損耗之間的關系，提出了一種MFT損耗最小化的優化設計方法，為MFT的設計提供了參考思路。

通過有限元仿真軟件，證明了本文的MFT設計方法可以減小損耗的同時減小漏感與電磁干擾的影響。同時研究了變壓器周圍電磁干擾的強弱情況，為外圍電路的放置位置提供參考。

最后，通過鐵心和繞組的定制化，制作了一臺應用于LLC諧振變換器的35kV絕緣、200kW、30kHz的MFT樣機。通過理論和實際的效率對比，驗證了本文方法的有效性和準確性。LLC諧振變換器的最高實測效率可達99.18%。同時變壓器也未出現散熱問題，在沒有考慮加入絕緣材料的條件下，變壓器的實測溫升遠低于設計要求，為后面繼續研究加入絕緣材料的MFT裕留足夠的溫升空間。

[1] 盧斯煜, 周保榮, 饒宏, 等. 高比例光伏發電并網條件下中國遠景電源結構探討[J]. 中國電機工程學報, 2018, 38(增刊1): 39-44.

Lu Siyu, Zhou Baorong, Rao Hong, et al. Research of the prospect of China power generation structure with high proportion of photovoltaic generation[J]. Pro- ceedings of the CSEE, 2018, 38(S1): 39-44.

[2] 丁明, 王偉勝, 王秀麗, 等. 大規模光伏發電對電力系統影響綜述[J]. 中國電機工程學報, 2014, 34(1): 1-14.

Ding Ming, Wang Weisheng, Wang Xiuli, et al. A review on the effect of large-scale PV generation on power systems[J]. Proceedings of the CSEE, 2014, 34(1): 1-14.

[3] Zhu Rongwu, Andresen M, Langwasser M, et al. Smart transformer/large flexible transformer[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(4): 264-274.

[4] Bahmani M A, Thiringer T, Rabiei A, et al. Com- parative study of a multi-MW high-power density DC transformer with an optimized high-frequency magnetics in all-DC off shore wind farm[J]. IEEE Transactions on Power Delivery, 2016, 31(2): 857- 866.

[5] She Xu, Huang A Q, Burgos R. Review of solid-state transformer technologies and their application in power distribution systems[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2013, 1(3): 186-198.

[6] 高范強, 李子欣, 李耀華, 等. 面向交直流混合配電應用的10kV-3MV·A四端口電力電子變壓器[J]. 電工技術學報, 2021, 36(16): 3331-3341.

Gao Fanqiang, Li Zixin, Li Yaohua, et al. 10kV- 3MV·A four-port power electronic transformer for AC-DC hybrid power distribution applications[J]. Transactions of China Electrotechnical Society, 2021, 36(16): 3331-3341.

[7] 胡鈺杰, 李子欣, 羅龍, 等. 基于串聯諧振間接矩陣型電力電子變壓器高頻電流特性分析及開關頻率設計[J]. 電工技術學報, 2022, 37(6): 1442-1454

Hu Yujie, Li Zixin, Luo Long, et al. Characteristic analysis of high-frequency-kink current of series resonant indirect matrix type power electronics transformer and switching frequency design[J]. Transactions of China Electrotechnical Society, 2022, 37(6): 1442-1454.

[8] 楊景剛, 張珂, 陳武, 等. 大功率中頻變壓器研究綜述[J]. 電源學報, 2020, 18(1): 4-17.

Yang Jinggang, Zhang Ke, Chen Wu, et al. Review on researches of high-power medium-frequency trans- former[J]. Journal of Power Supply, 2020, 18(1): 4-17.

[9] 王迎迎, 程紅. 應用于功率變換器的多繞組高頻變壓器模型[J]. 電工技術學報, 2021, 36(19): 4140- 4147.

Wang Yingying, Cheng Hong. Dual multi-winding high-frequency transformer equivalent circuit for power converter applications[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 4140-4147.

[10] 張航, 李耀華, 高范強, 等. 級聯H橋型電力電子變壓器隔離級高頻電流波動抑制策略[J]. 電力系統自動化, 2020, 44(7): 130-138.

Zhang Hang, Li Yaohua, Gao Fanqiang, et al. High- frequency current fluctuation suppression strategy for isolation stage of cascaded H-bridge based power electronic transformer[J]. Automation of Electric Power Systems, 2020, 44(7): 130-138.

[11] Zheng Jialin, Zhao Zhengming, Shi Bochen, et al. A discrete state event driven simulation based losses analysis for multi-terminal megawatt power electronic transformer[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(4): 275-284.

[12] 趙爭菡, 汪友華, 凌躍勝, 等. 大容量高頻變壓器繞組損耗的計算與分析[J]. 電工技術學報, 2014, 29(5): 261-264, 270.

Zhao Zhenghan, Wang Youhua, Ling Yuesheng, et al. Calculation and analysis of loss in high-capacity high- frequency transformers[J]. Transactions of China Elec- trotechnical Society, 2014, 29(5): 261-264, 270.

[13] 張重遠, 王增超, 張欣, 等. 基于改進矢量匹配法的變壓器鐵芯頻變渦流模型[J]. 高電壓技術, 2015, 41(5): 1618-1623.

Zhang Zhongyuan, Wang Zengchao, Zhang Xin, et al. Transformer core modeling for frequency dependent eddy current based on modified vector fitting[J]. High Voltage Engineering, 2015, 41(5): 1618-1623.

[14] 李子欣, 高范強, 趙聰, 等. 電力電子變壓器技術研究綜述[J]. 中國電機工程學報, 2018, 38(5): 1274-1289.

Li Zixin, Gao Fanqiang, Zhao Cong, et al. Research review of power electronic transformer technolo- gies[J]. Proceedings of the CSEE, 2018, 38(5): 1274- 1289.

[15] Dowell P L. Effects of eddy currents in transformer windings[J]. Proceedings of the Institution of Electrical Engineers, 1966, 113(8): 1387-1394.

[16] Ferreira J A. Improved analytical modeling of con- ductive losses in magnetic components[J]. IEEE Transactions on Power Electronics, 1994, 9(1): 127- 131.

[17] Agheb E, H?idalen H K. Medium frequency high power transformers, state of art and challenges[C]// 2012 International Conference on Renewable Energy Research and Applications (ICRERA), Nagasaki, 2012: 1-6.

[18] 楊東江, 段彬, 丁文龍, 等. 一種帶輔助雙向開關單元的寬輸入電壓范圍LLC諧振變換器[J]. 電工技術學報, 2020, 35(4): 775-785.

Yang Dongjiang, Duan Bin, Ding Wenlong, et al. An improved LLC resonant converter with auxiliary bi-directional switch for wide-input-voltage range applications[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 775-785.

[19] 劉瑞欣, 王議鋒, 韓富強, 等. 應用于寬輸入電壓范圍的兩模式切換型軟開關諧振直流變換器[J]. 電工技術學報, 2020, 35(22): 4739-4749.

Liu Ruixin, Wang Yifeng, Han Fuqiang, et al. A two- mode soft-switching resonant DC-DC converter for wide input voltage range applications[J]. Transactions of China Electrotechnical Society, 2020, 35(22): 4739-4749.

[20] 劉碩, 蘇建徽, 賴紀東, 等. LLC諧振變換器PO模式增益公式與模式邊界條件分析[J]. 電力系統自動化, 2020, 44(6): 164-170.

Liu Shuo, Su Jianhui, Lai Jidong, et al. Analysis on gain formula and mode boundary condition for LLC resonant converter in PO mode[J]. Automation of Electric Power Systems, 2020, 44(6): 164-170.

[21] Hurley W G, W?lfle W H. Transformers and indu- ctors for power electronics, theory, design and applications[M]. Chichester: John Wiley & Sons, 2013.

[22] Yu Xiong, Su Jianhui, Lai Jidong, et al. Analytical optimization of nonsaturated thermally limited high- frequency transformer/inductor design considering discreteness of design variables[J]. IEEE Transactions on Power Electronics, 2020, 35(6): 6231-6250.

[23] 曹小鵬, 陳武, 寧光富, 等. 基于多目標遺傳算法的大功率高頻變壓器優化設計[J]. 中國電機工程學報, 2018, 38(5): 1348-1355.

Cao Xiaopeng, Chen Wu, Ning Guangfu, et al. Optimization design of high-power high-frequency transformer based on multi-objective genetic algo- rithm[J]. Proceedings of the CSEE, 2018, 38(5): 1348-1355.

[24] Leibl M, Ortiz G, Kolar J W. Design and experimental analysis of a medium-frequency transformer for solid- state transformer applications[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2017, 5(1): 110-123.

[25] Bahmani M A, Thiringer T, Kharezy M. Design metho- dology and optimization of a medium-frequency transformer for high-power DC-DC applications[J]. IEEE Transactions on Industry Applications, 2016, 52(5): 4225-4233.

[26] 律方成, 郭云翔, 李鵬. 大功率中頻變壓器多目標參數優化設計[J]. 高電壓技術, 2017, 43(1): 210- 217.

Lü Fangcheng, Guo Yunxiang, Li Peng. Optimization design for multiple target parameters of high power medium frequency transformer[J]. High Voltage Engineering, 2017, 43(1): 210-217.

[27] Venkatachalam K, Sullivan C R, Abdallah T, et al. Accurate prediction of ferrite core loss with non- sinusoidal waveforms using only Steinmetz para- meters[C]//IEEE Workshop on Computers in Power Electronics, Mayaguez, 2002: 36-41.

[28] Kazimierczuk M K. High-frequency magnetic com- ponents[M]. Chichester: John Wiley & Sons, 2014: 338-351.

[29] Wojda R P, Kazimierczuk M K. Winding resistance of Litz-wire and multi-strand inductors[J]. IET Power Electronics, 2012, 5(2): 257-268.

[30] Mogorovic M, Dujic D. Medium frequency trans- former leakage inductance modeling and experimental verification[C]//2017 IEEE Energy Conversion Con- gress and Exposition (ECCE), Cincinnati, 2017: 419-424.

An Optimal Design Method for Medium-Voltage Insulated High-Power Medium-Frequency Transformer

（College of Electrical Engineering and Automation Hefei University of Technology Hefei 230009 China）

The medium-voltage insulated high-power medium-frequency transformer (MFT) used in photovoltaic grid-connected systems not only requires a large insulation distance between the high and low voltage side windings, but also needs to be poured with thermal-protective insulating materials inside. However, it can lead to problems such as serious electromagnetic interference and difficult heat dissipation in the MFT. Therefore, this paper proposes an MFT optimal design method that fully considers the core size, winding wire diameter and winding arrangement structure. In this method, the core volume is determined by the area product (AP) method, and then the loss of the MFT is minimized by free variable scanning. Based on the finite element simulation software, it is verified that the optimized design method will also reduce the electromagnetic interference area around the transformer. Finally, a 200kW/30kHz MFT was designed through the optimized design method, and a prototype was made. The comparison between theory and experiment verifies the optimized design method.

High-power medium-frequency transformer, insulation, area product method, loss modeling, optimal design, electromagnetic interference, finite element simulation

10.19595/j.cnki.1000-6753.tces.211799

TM432

國家自然科學基金面上項目（52077051）、合肥綜合性國家科學中心能源研究院項目（19KZS207, 21KZS203）和高等學校學科創新引智計劃項目（BP0719039）資助。

2021-11-04

2022-02-11

王佳寧 男，1985年生，副教授，研究方向為電力設備的封裝和可靠性測試、電力電子轉換器的集成、寬帶隙電力設備的應用、電磁建模。E-mail: 16002530@163.com

胡嘉汶 男，1997年生，碩士研究生，研究方向為多相LLC諧振變換器設計與大功率中頻變壓器的優化設計。E-mail: hjw970604@qq.com（通信作者）

（編輯 陳 誠）