輻射型直流配電網母線電壓跌落峰值的定量計算方法

唐 欣 蔡明君 唐惟楚 岳雨霏 尹子晨 彭 超

輻射型直流配電網母線電壓跌落峰值的定量計算方法

唐 欣 蔡明君 唐惟楚 岳雨霏 尹子晨 彭 超

（長沙理工大學電氣與信息工程學院 長沙 410000）

區別于交流配電網，直流配電網中電源具有低慣性特性，當配電網負載突變時，直流母線電壓波動較大，母線電壓質量面臨巨大挑戰。在解決直流配電網慣性低的問題上，可采用超級電容增加物理慣性或者采用虛擬電容（需要變流器配置冗余容量提供）增加虛擬慣性，配置的電容越大，供電質量越高，但成本也會越高。然而，目前關于電容對電壓跌落幅度抑制作用的研究以定性分析為主，缺乏定量計算。為此，該文對輻射型直流配電網中直流母線電壓在負載突增下的暫態響應進行分析，求得母線電壓跌落峰值與聯絡變流器直流側電容值之間的數學關系，為系統慣性參數設計提供理論支持。由于獲得的數學關系式比較復雜，為方便工程應用，設計簡化方法，得到近似的代數關系。最后，利用仿真和實驗對電壓跌落峰值計算方法進行了驗證，仿真與實驗結果驗證該文所提計算方法的正確性。

直流配電網 低慣性特性 電壓跌落 抑制電壓跌落峰值計算

0 引言

相比于交流配電網，直流配電網具有建設成本低、電能損耗小、供電可靠性高、環保等優點，在快速獨立地控制有功和無功、減少電能變換環節、改善用戶側電能質量等方面具有獨特優勢，是未來智能配電系統中的重要組成部分[1-4]。雖然直流配電網不存在功角穩定、頻率穩定等問題，但由于電源的慣性較小，負載的投切會引起直流母線電壓劇烈波動，對直流母線暫態電壓質量造成沖擊甚至影響到直流配電網的安全穩定運行[5-6]。

在解決直流配電網電壓質量問題上，一種方法采取在直流母線上并聯超級電容（Super Capacitor, SC）等措施增加直流配電網的物理慣性[7-11]。文獻[7]對直流母線電壓波動范圍進行等級劃分，提出不同等級應采取不同的控制方案，但只是劃定了大致的范圍，并未給出超級電容與電壓波動峰值之間的定量關系。文獻[8]提出超級電容的加入對系統慣量阻尼特性的提升有顯著效果，并指出系統等效的慣量阻尼特性受穩態工作點、結構參數以及控制器參數等的共同影響，但也只是定性分析不同參數對電壓波動抑制效果的影響。文獻[9]優化了超級電容的控制方法，可有效治理直流母線電壓暫降，但并未分析電壓降落的最小值與超級電容值之間的關系，只是在假定電壓已經降落到最小值的基礎上定性地分析超級電容的控制策略對電壓恢復的影響。文獻[10-11]雖然在設計直流電容時計算了負載突變產生電壓跌落的峰值，但均未考慮控制的作用，計算過于粗略。

另一種方法是通過改進聯絡變流器的控制策略來增加直流配電網的虛擬慣性。有學者通過類比交流電網中的虛擬同步發電機（Virtual Synchronous Generator, VSG）控制[12-15]，提出了直流配電網中的虛擬電容（Virtual Capacitor, VC）控制[16-22]。文獻[16]融合VSG控制與下垂控制，提出一種適用于雙向并網變換器的虛擬電容控制策略，平抑了直流母線電壓波動。文獻[17]提出了一種適用于多端口隔離型DC-DC變換器的改進VSG控制策略，并給出相應參數整定設計的方法，可推廣至其他DC-DC變換器。文獻[18]提出一種AVSG控制策略來增強直流微電網的慣性和阻尼，其啟動特性及動靜態特性俱佳，且該文在抑制電壓振蕩的基礎上，通過根軌跡法分析了控制策略對系統穩定性的影響。文獻[19-20]提出了靈活虛擬慣性控制策略，對虛擬電容參數自適應進行了研究。文獻[21]通過對主要控制參數進行靈敏度分析，研究了參數對直流母線電壓波動影響的規律。文獻[22]提出了一種基于VSG的靈活虛擬電容控制策略，并利用李雅普諾夫穩定性判據確定了控制參數的穩定運行邊界。上述虛擬電容控制策略雖然有效減緩了負荷突變時直流母線電壓的波動，但只針對穩定邊界判定、靈敏度分析等方面進行了定量分析，而針對虛擬電容對電壓波動的抑制作用也只是進行了定性分析。

配置的電容越大，供電質量越高，但成本也會越高。然而，無論是考慮增加物理慣性還是虛擬慣性，目前關于超級電容或虛擬電容（需要變流器配置冗余容量提供）對直流母線電壓波動抑制的理論分析與實驗都停留在定性分析。因此，有必要研究直流母線電壓跌落峰值的理論計算方法，為聯絡變流器直流側電容的合理配置提供理論依據。為此，本文對聯絡變流器等效控制模型進行近似處理與化簡，推導出直流母線電壓在負荷擾動下的閉環傳遞函數，通過暫態特性分析以及線性化處理得到簡明且相對保守的代數關系，最終得到電壓跌落峰值的定量計算公式，獲得保證最大沖擊負載下電能質量的最小電容配置值。

1 系統描述

1.1 一次系統描述

本文以安徽金梧桐直流配電系統示范工程為研究對象，該系統接入了交直流聯絡變流器、光伏電池、儲能電池、超級電容和充電樁等設備，控制方式為主從控制[23-25]，聯絡變流器采用定直流母線電壓控制來平衡系統功率。圖1給出了直流配電系統的結構示意圖，圖中，和分別為聯絡變流器網側濾波電感和等效電阻；sabc為變壓器二次電壓；sabc為流過濾波電感的電流；cabc為聯絡變流器交流側電壓；dc和VSC分別為聯絡變流器直流側電壓（直流母線電壓）和直流側電流；dc0為聯絡變流器直流側支撐電容；SC為連接在直流母線上的超級電容；i1為流過聯絡變流器支撐電容的電流；i2為流過超級電容的電流；dc為直流母線流入直流配電網的電流。

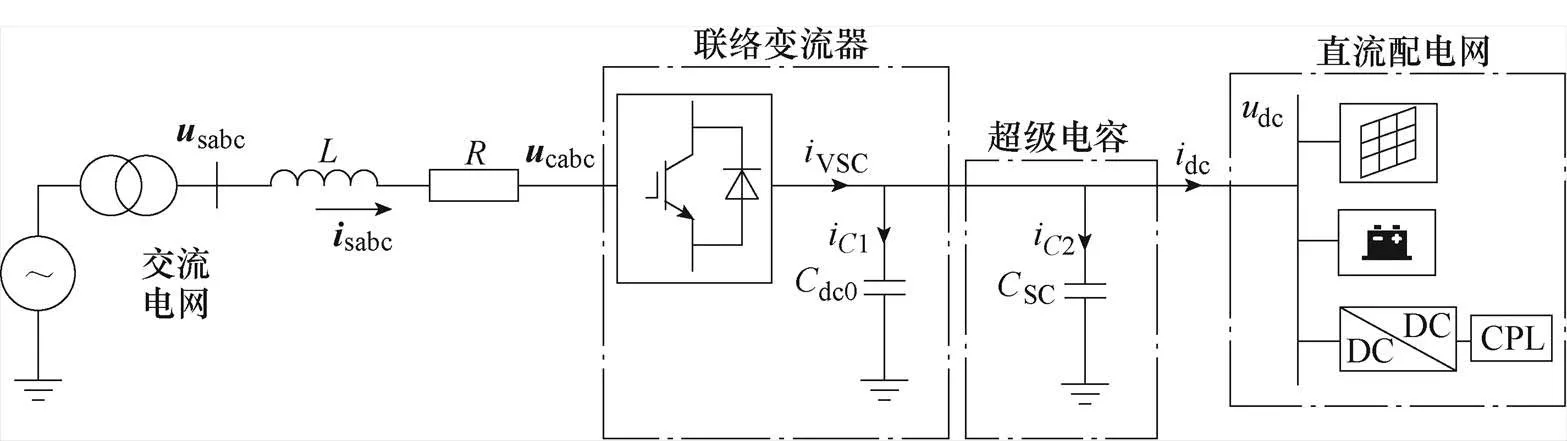
圖1 直流配電系統

1.2 控制系統描述

聯絡變流器采用雙閉環前饋解耦控制，外環采用定直流母線電壓控制方式，內環采用電流矢量控制方式，控制策略如圖2所示。圖中，為交流電網基波角頻率；sd和sq分別為sabc的d軸和q軸分量；sd和sq分別為sabc的d軸和q軸分量；cd和cq分別為cabc的d軸和q軸分量；i()=pi+ii/為電流調節器，pi、ii分別為電流環比例和積分系數；u()=pu+iu/為電壓調節器，pu、iu分別為電壓環比例和積分系數。文中大寫表示對應變量的穩態值，上標*表示對應變量的指令值，后面不再重復說明。

圖2 聯絡變流器前饋解耦控制策略

2 暫態電壓跌落峰值計算

2.1 聯絡變流器等效控制模型及化簡分析

圖3所示為聯絡變流器等效控制模型[26]。圖中，G()=1/(dc)為直流側等效電容傳遞函數，其中dc=dc0+SC為直流側等效電容；i=i1+i2為流過dc的等效電流；ci()為電流內環等效傳遞函數；為PWM的調制比；0為穩態時開關函數基波 相位。

穩態時，忽略，根據功率平衡方程，有

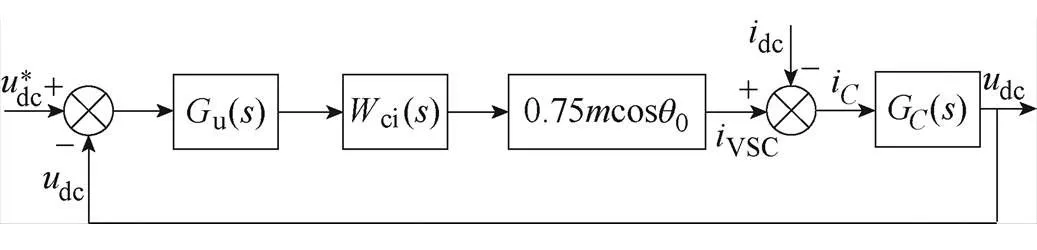
圖3 聯絡變流器等效控制模型

式中，=L為變流器濾波電感的電抗值。

又有

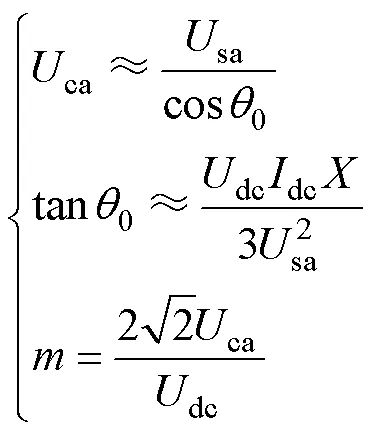
將式（2）合并化簡后有

式中，T為轉換系數。

由于電流內環的帶寬遠大于電壓外環，因此閉環傳遞函數ci()可近似為1，圖3所示的結構可簡化為如圖4所示。

圖4 變流器控制簡化結構

由圖4可得變流器控制傳遞函數表達式為

其中

由式（5）可知，若穩定運行時負荷突增，則有

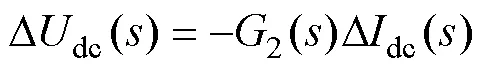
將2()展開后，可得

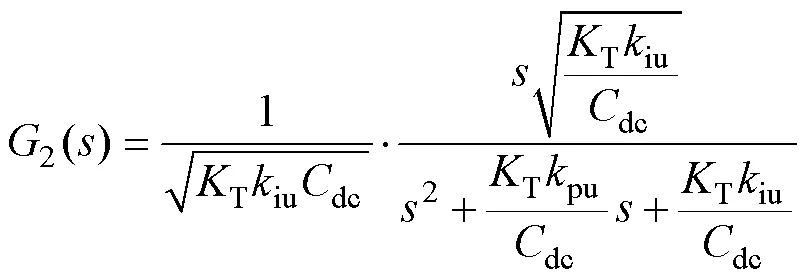
根據終值定理，由式（7）可知，直流母線電壓對負荷擾動的穩態響應為0，因此可以通過計算系統響應的超調量來計算電壓跌落峰值。

2.2 暫態電壓跌落峰值與電容值關系計算

將負荷擾動下的閉環傳遞函數轉換為包含微分環節和常系數的二階模型，即

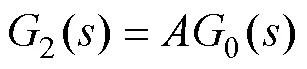
其中

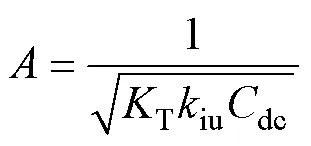
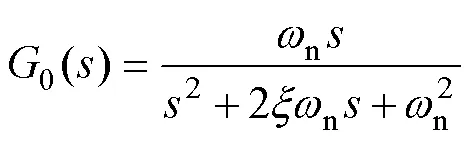
式中，自然角頻率n和阻尼比分別為

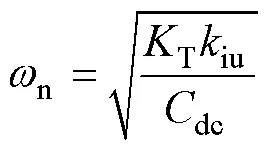
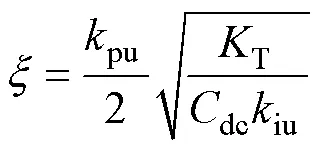
對于0()，其單位階躍響應為

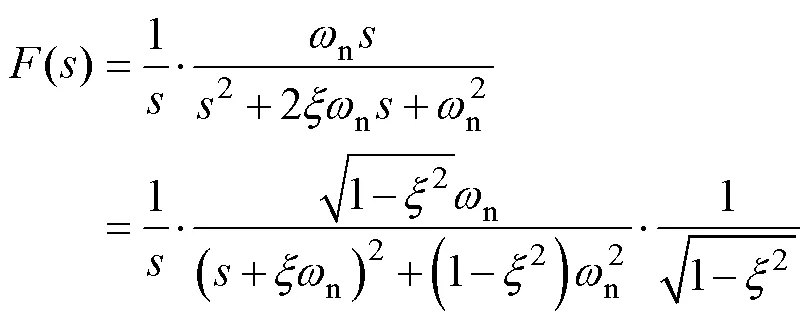
令

則有

為求()的極值，對()求導得

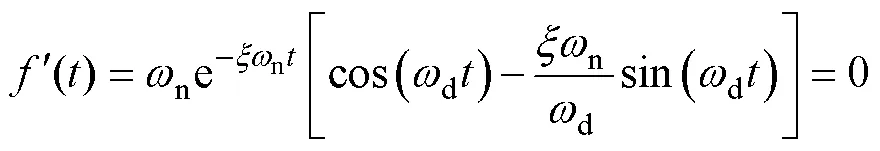
整理得

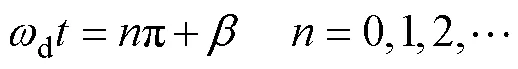
其中

系統穩定前提下，響應的第一個峰值時間達到最大超調量，取=1，有第一個峰值時間為

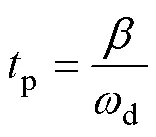
將峰值時間p代入式（16），得最大峰值為

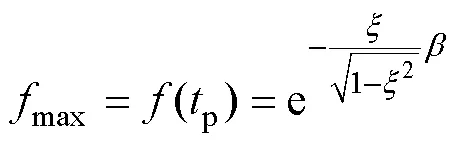
結合式（8）、式（20），可得到電壓跌落峰值與電容之間的關系，但關系式太復雜，不便于工程應用。為此，將式（20）線性化，簡化電壓跌落峰值與電容之間的關系式（為保證式（23）的簡明且可反解出dc，未采用高次擬合）。由式（20）畫max關于的曲線如圖5所示，設在0～0（對應dc為+∞～dc0）范圍內變化，則可用直線近似這段曲線。取描述這段直線的函數為

因此，負荷突增后的電壓跌落峰值近似為

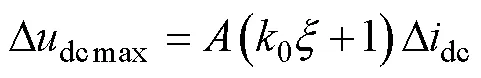
展開式（22），有

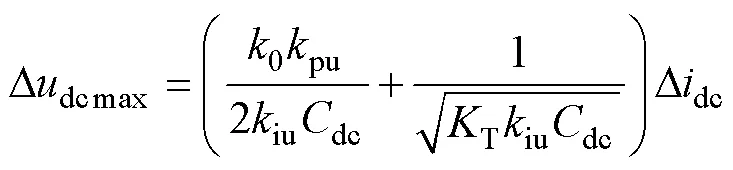
由式（23）可知，隨著電容的增加，在相同負荷擾動下，電壓波動的幅值減小。由于圖5中直線位于曲線上方，式（23）近似計算得到電壓跌落峰值更大，說明近似計算值更為保守。

式（23）給出了Ddcmax對于電容dc的表達式，將其反解，可得電容dc對于Ddcmax的表達式為

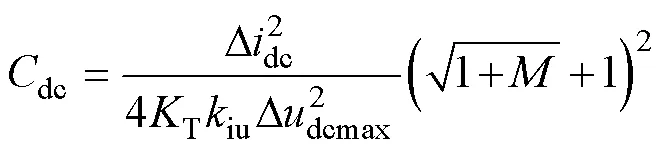
其中

式（23）、式（24）反映了電容與暫態電壓跌落峰值之間的關系，為滿足母線暫態電壓質量要求下電容值的選取提供了理論依據。可通過最大沖擊負載確定Ddc的取值，根據電能質量的要求確定Ddcmax的取值，從而求得最小慣性電容dc的配置值。

由式（23）可得負荷突增后直流母線電壓最小值dcmin為

從式（23）中還可以看出，聯絡變流器的控制參數也對電壓跌落幅度有影響：①iu與dc處于式（23）相同位置，因此變化規律近似相同，增大iu后Ddcmax減小；②由于線性化后0為負，增大pu后Ddcmax減小。

3 仿真與實驗驗證

為了驗證本文計算方法的正確性，本文利用Matlab/Simulink仿真軟件和實驗平臺進行證明，仿真和實驗系統如圖1所示，系統主要參數見表1。由于光伏電池、儲能電池以及復雜結構的負荷可能對直流電壓質量有積極的影響，而超級電容的配置需要考慮系統在極端工況下的正常運行，因此在仿真和實驗時停運光伏電池、儲能電池等設備且負載側采用恒功率負載。

表1 直流配電系統主要參數

Tab.1 Main parameters of DC distribution system

3.1 仿真證明

3.1.1 工況1：負載突增

圖6所示為不同超級電容下負荷突增時，直流母線電壓跌落的仿真波形，仿真中，在1s時負載突增2.7kW。圖中，SC取0～8mF間不同值（間隔為1mF），從圖中可知，SC越大，對電壓跌落抑制作用越強。

圖6 工況1下，不同超級電容值時直流母線電壓跌落仿真波形

測出圖6中不同超級電容下負荷突增后直流母線電壓最小值dcmin，然后與式（25）計算出的dcmin進行比較，比較結果如圖7所示。從圖中可知，dcmin(pu)的計算值與仿真值之差小于2%，驗證了計算方法的正確性。

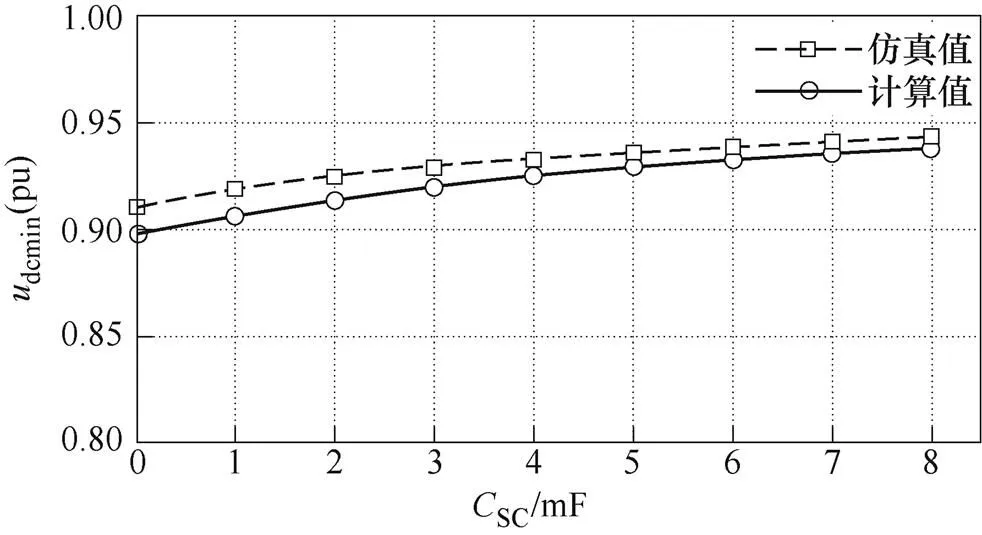
圖7 工況1下，不同超級電容值時udcmin仿真值與計算值的對比

3.1.2 工況2：與工況1不同控制參數時負載突增

為考察本文方法對不同工況的適用性，改變電壓外環的PI參數（pu=0.2，iu=10），且負載突增量變成5.4kW。圖8所示為改變參數后負載突增時，直流母線電壓跌落的仿真波形，仿真中，在1s時負載突增5.4kW。圖中SC分別為0～8mF（間隔為1mF），從圖中可知，SC越大，對電壓跌落抑制作用越強。

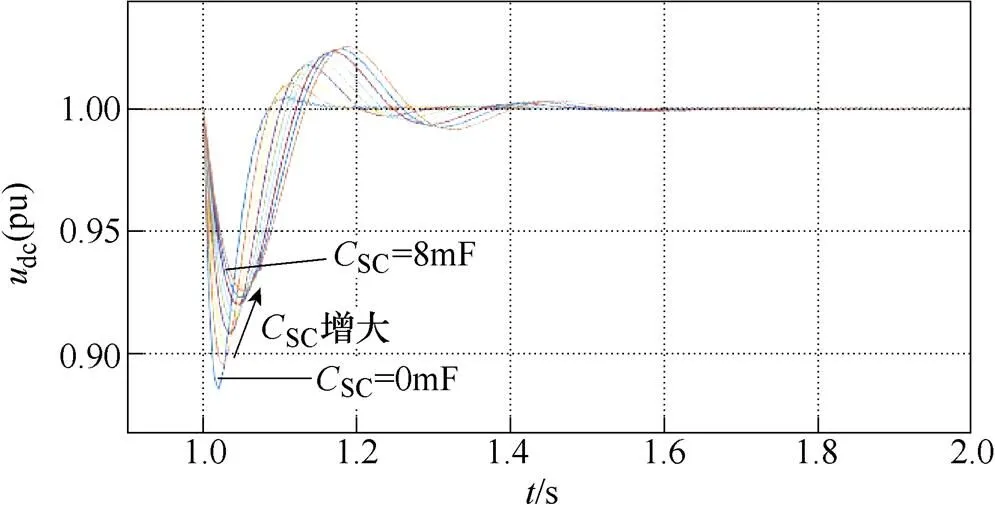
圖8 工況2下，不同超級電容值時直流母線電壓跌落仿真波形

測出圖8中不同超級電容下負荷突增后直流母線電壓最小值dcmin，然后與式（25）計算出的dcmin進行比較，比較結果如圖9所示。從圖中可知，dcmin(pu)的計算值與仿真值之差小于2%，再次驗證了計算方法的正確性。

3.1.3 工況3：負載突減

雖然理論部分是基于負載突增時電壓跌落情況下的定量計算，但從式（23）的推導過程可知，式（23）同樣適用于負載突減時直流母線電壓驟升峰值的定量計算（此時式（23）中電流為負）。工況3給出保持表1參數不變（與工況1同參數）的情況下，負載突減時的仿真結果。

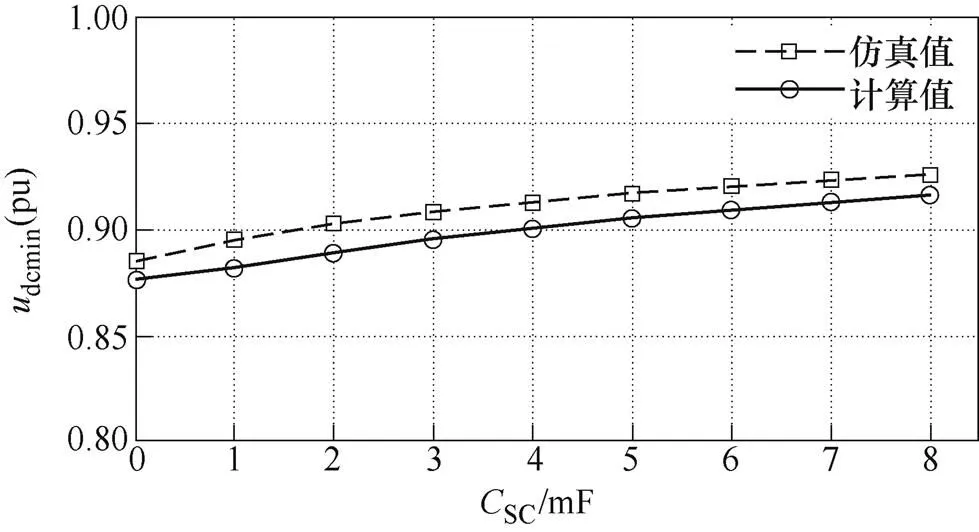
圖9 工況2下，不同超級電容值時udcmin仿真值與計算值的對比

圖10所示為不同超級電容值下負荷突減時，直流母線電壓驟升的仿真波形，仿真中，在1s時負載突減2.7kW。圖中SC取0～8mF間的值（間隔為1mF）。測出圖10中不同超級電容值下負載突減后直流母線電壓最大值dcmax，然后與dcmax的計算值進行比較，比較結果如圖11所示。從圖中可知，式（23）同樣適用于負載突減工況下的定量計算。

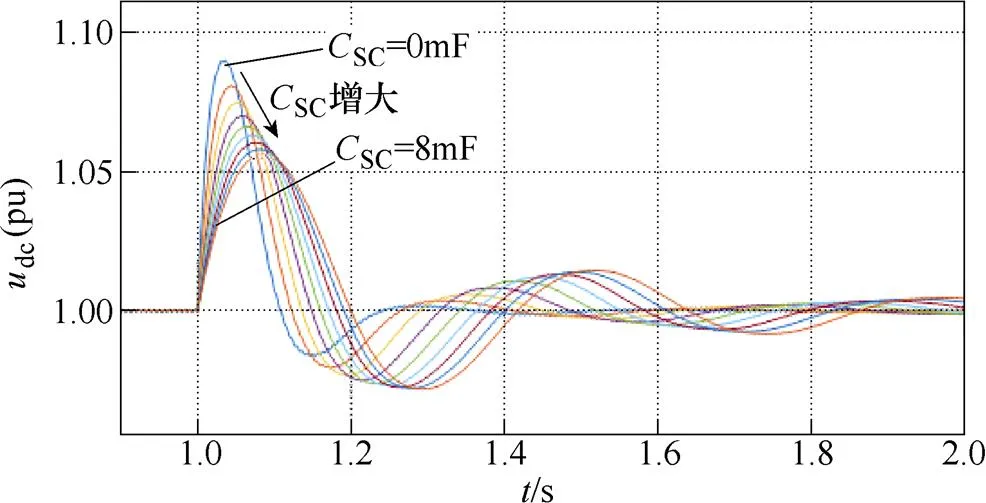
圖10 工況3下，不同超級電容值時直流母線電壓驟升仿真波形

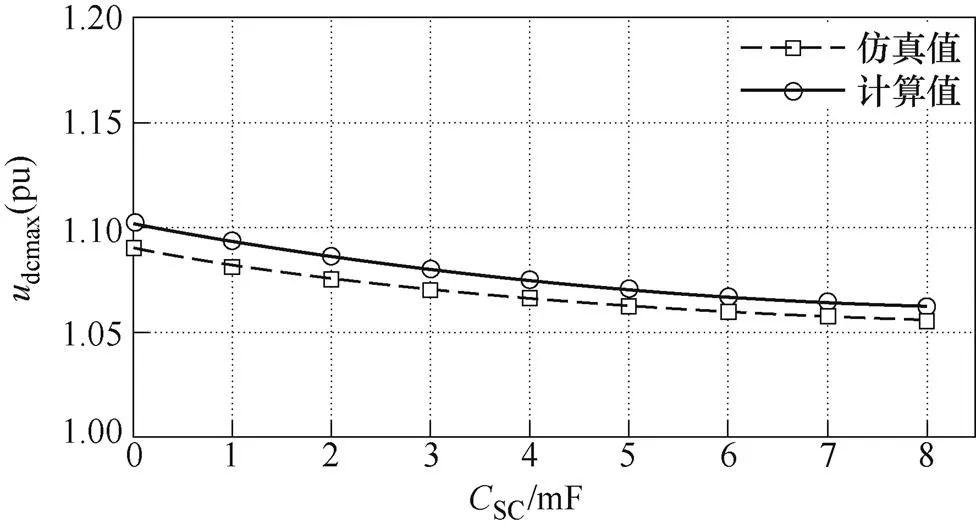
圖11 工況3下，不同超級電容值時udcmax仿真值與計算值的對比

3.2 實驗驗證

為了進一步驗證本文計算方法的正確性，在直流配電網平臺進行了實驗驗證，考慮到實驗設備的安全性及對現有設備的充分利用，負載突增量取2.7kW。圖12為實驗平臺實物。

圖12 實驗平臺實物

圖13所示為未加入超級電容，等效電容dc=dc0=2 040mF時，直流母線電壓跌落的實驗波形。從圖中可知，負載突增2.7kW后，直流母線電壓最小值dcmin=403.78V。由式（25）計算得到dcmin= 404.14V，計算值與實驗值之差小于額定值的0.1%，證明本文計算方法的正確性。

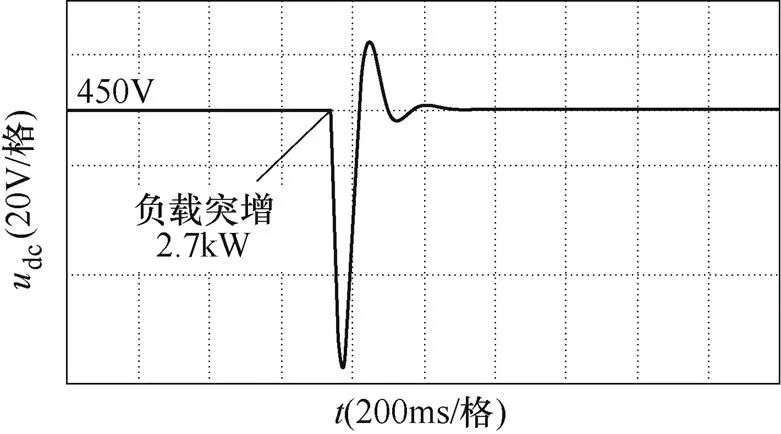
圖13 未加入超級電容時，直流母線電壓跌落實驗波形

圖14所示為加入超級電容后，SC=8mF時，直流母線電壓跌落的實驗波形。從圖中可知，負載突增2.7kW后，直流母線電壓最小值dcmin=425.66V。因此，加入超級電容后，直流母線電壓跌落得到了顯著抑制。

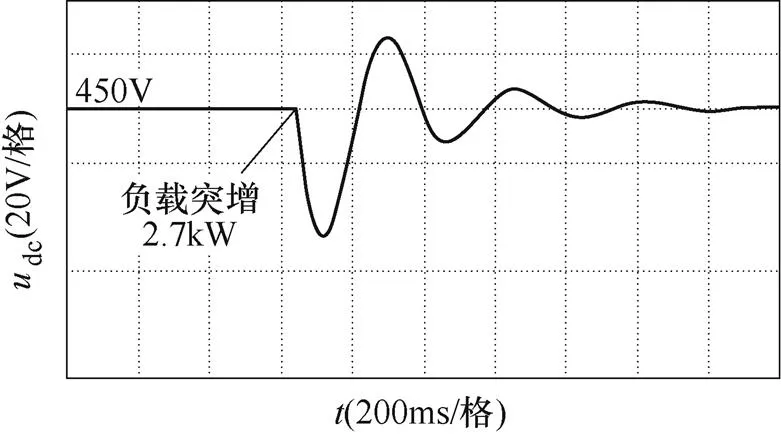
圖14 加入超級電容后，直流母線電壓跌落實驗波形

圖15所示為加入超級電容后，SC分別取0～8mF（間隔為1mF）時，dcmin實驗值與計算值的對比。實驗中，負載突增2.7kW，而計算值同仿真驗證時所述一致。從圖中可知，dcmin(pu)的計算值與實驗值之差小于2%，再次從實驗的角度驗證了計算方法的正確性。

圖15 不同超級電容值下udcmin實驗值與計算值的對比

4 結論

由于直流配電網中電源的低慣性特性容易產生電壓質量問題。系統中配置慣性電容越大，供電質量越高，但成本也會越高。為合理配置系統的電容，本文以輻射型主從控制的直流配電網為對象，研究了直流母線電壓跌落的峰值定量計算及抑制方法，得出如下結論：

1）直流配電網母線電壓質量與聯絡變流器直流側等效電容大小強相關，但不是線性關系，等效電容越大，電壓波動越小。可以通過分析系統對擾動的暫態響應，求得聯絡變流器直流側電壓跌落峰值與其直流側等效電容值之間的數學關系，為慣性電容配置提供理論依據。

2）式（23）同樣適用于切負荷時電壓突增的情況。本文為了論述的簡潔性，僅針對電壓跌落時的暫態過程進行分析。

3）為簡化計算，式（3）中參數dc取為直流電壓穩態值，造成了電壓跌落峰值的計算值同仿真與實驗值存在一定誤差。

[1] 李海波, 趙宇明, 劉國偉, 等. 基于時序仿真的商業樓宇交流與直流配電系統能效對比[J]. 電工技術學報, 2020, 35(19): 4194-4206.

Li Haibo, Zhao Yuming, Liu Guowei, et al. The time sequential simulation based energy efficiency com- parison of AC and DC distribution power system in commercial buildings[J]. Transactions of China Elec- trotechnical Society, 2020, 35(19): 4194-4206.

[2] 梁永亮, 吳躍斌, 馬釗, 等. 新一代低壓直流供用電系統在“新基建”中的應用技術分析及發展展望[J]. 中國電機工程學報, 2021, 41(1): 13-24.

Liang Yongliang, Wu Yuebin, Ma Zhao, et al. Appli- cation and development prospect of new generation of LVDC supply and utilization system in “new infrastructure”[J]. Proceedings of the CSEE, 2021, 41(1): 13-24.

[3] 金國彬, 潘狄, 陳慶, 等. 考慮源荷不確定性的直流配電網模糊隨機日前優化調度[J]. 電工技術學報, 2021, 36(21): 4517-4528.

Jin Guobin, Pan Di, Chen Qing, et al. Fuzzy random day-ahead optimal dispatch of DC distribution network considering the uncertainty of source-load[J]. Transactions of China Electrotechnical Society, 2021, 36(21): 4517-4528.

[4] Shamsoddini M, Vahidi B, Razani R, et al. A novel protection scheme for low voltage DC microgrid using inductance estimation[J]. International Journal of Electrical Power & Energy Systems, 2020, 120: 105992.

[5] Dragi?evi? T, Guerrero J M, Vasquez J C, et al. Supervisory control of an adaptive-droop regulated DC microgrid with battery management capability[J]. IEEE Transactions on Power Electronics, 2014, 29(2): 695-706.

[6] Wu T F, Chang C H, Lin L C, et al. DC-bus voltage control with a three-phase bidirectional inverter for DC distribution systems[J]. IEEE Transactions on Power Electronics, 2013, 28(4): 1890-1899.

[7] 張繼紅, 趙銳, 高雷, 等. 直流微網母線電壓穩定控制策略[J/OL]. 電網技術, 2021, http://kns.cnki. net/kcms/detail/11.2410.TM.20210101.1431.002.html.

Zhang Jihong, Zhao Rui, Gao Lei, et al. DC bus voltage stability control strategy for DC micro- grid[J/OL]. Power System Technology, 2021, http:// kns.cnki.net/kcms/detail/11.2410.TM.20210101.1431.002.html.

[8] 農仁飚, 楊曉峰, 周兵凱, 等. 基于低壓直流母線系統的慣量阻尼特性研究[J]. 電網技術, 2021, 45(11): 4512-4522.

Nong Renbiao, Yang Xiaofeng, Zhou Bingkai, et al. Inertia and damping characteristics of LVDC system[J]. Power System Technology, 2021, 45(11): 4512-4522.

[9] 馬智遠, 欒樂, 許中, 等. 一種基于超級電容的變頻器電壓暫降治理裝置[J]. 電力電子技術, 2020, 54(12): 60-63.

Ma Zhiyuan, Luan Le, Xu Zhong, et al. A voltage sag mitigation device for adjustable speed drives based on super capacitor[J]. Power Electronics, 2020, 54(12): 60-63.

[10] 王久和, 李華德, 王立明. 電壓型PWM整流器直接功率控制系統[J]. 中國電機工程學報, 2006, 26(18): 54-60.

Wang Jiuhe, Li Huade, Wang Liming. Direct power control system of three phase Boost type PWM rectifiers[J]. Proceedings of the CSEE, 2006, 26(18): 54-60.

[11] 史偉偉, 蔣全, 胡敏強, 等. 三相電壓型PWM整流器的數學模型和主電路設計[J]. 東南大學學報(自然科學版), 2002, 32(1): 50-55.

Shi Weiwei, Jiang Quan, Hu Minqiang, et al. Mathematical model and main circuit design of three- phase voltage-source PWM rectifier[J]. Journal of Southeast University (Science and Technology), 2002, 32(1): 50-55.

[12] Zhong Qingchang, Nguyen P L, Ma Zhenyu, et al. Self-synchronized synchronverters: inverters without a dedicated synchronization unit[J]. IEEE Transa- ctions on Power Electronics, 2014, 29(2): 617-630.

[13] 石榮亮, 張興, 徐海珍, 等. 光儲柴獨立微電網中的虛擬同步發電機控制策略[J]. 電工技術學報, 2017, 32(23): 127-139.

Shi Rongliang, Zhang Xing, Xu Haizhen, et al. A control strategy for islanded photovoltaic-battery- diesel microgrid based on virtual synchronous generator[J]. Transactions of China Electrotechnical Society, 2017, 32(23): 127-139.

[14] 伍文華, 陳燕東, 周樂明, 等. 虛擬同步發電機接入弱電網的序阻抗建模與穩定性分析[J]. 中國電機工程學報, 2019, 39(6): 1560-1571, 1853.

Wu Wenhua, Chen Yandong, Zhou Leming, et al. Sequence impedance modeling and stability analysis for virtual synchronous generator connected to the weak grid[J]. Proceedings of the CSEE, 2019, 39(6): 1560-1571, 1853.

[15] 于鴻儒, 蘇建徽, 徐華電, 等. 并網逆變器虛擬慣性與阻尼的等效及辨識[J]. 中國電機工程學報, 2019, 39(20): 6034-6043, 6184.

Yu Hongru, Su Jianhui, Xu Huadian, et al. Equivalent and identification of virtual inertia and damping of grid-connected inverter[J]. Proceedings of the CSEE, 2019, 39(20): 6034-6043, 6184.

[16] 伍文華, 陳燕東, 羅安, 等. 一種直流微網雙向并網變換器虛擬慣性控制策略[J]. 中國電機工程學報, 2017, 37(2): 360-371.

Wu Wenhua, Chen Yandong, Luo An, et al. A virtual inertia control strategy for bidirectional grid-connected converters in DC micro-grids[J]. Proceedings of the CSEE, 2017, 37(2): 360-371.

[17] 張輝, 梁譽馨, 孫凱, 等. 直流微電網中多端口隔離型DC-DC變換器的改進虛擬電容控制策略[J]. 電工技術學報, 2021, 36(2): 292-304.

Zhang Hui, Liang Yuxin, Sun Kai, et al. Improved virtual capacitor control strategy of multi-port isolated DC-DC converter in DC microgrid[J]. Transactions of China Electrotechnical Society, 2021, 36(2): 292- 304.

[18] 朱曉榮, 孟凡奇, 謝志云. 基于虛擬同步發電機的直流微網DC-DC變換器控制策略[J]. 電力系統自動化, 2019, 43(21): 132-140.

Zhu Xiaorong, Meng Fanqi, Xie Zhiyun. Control strategy of DC-DC converter in DC microgrid based on virtual synchronous generator[J]. Automation of Electric Power Systems, 2019, 43(21): 132-140.

[19] 鄒培根, 孟建輝, 王毅, 等. 一種直流微電網的靈活虛擬慣性控制策略[J]. 電力建設, 2018, 39(6): 56-62.

Zou Peigen, Meng Jianhui, Wang Yi, et al. A flexible virtual inertia control strategy for DC microgrid[J]. Electric Power Construction, 2018, 39(6): 56-62.

[20] Wang Chen, Meng Jianhui, Wang Yi, et al. Adaptive virtual inertia control for DC microgrid with variable droop coefficient[C]//International Conference on Electrical Machines and Systems, Sydney, Australia, 2017: 1-5.

[21] 孟建輝, 鄒培根, 王毅, 等. 基于靈活虛擬慣性控制的直流微網小信號建模及參數分析[J]. 電工技術學報, 2019, 34(12): 2615-2626.

Meng Jianhui, Zou Peigen, Wang Yi, et al. Small- signal modeling and parameter analysis of the DC microgrid based on flexible virtual inertia control[J]. Transactions of China Electrotechnical Society, 2019, 34(12): 2615-2626.

[22] 孟建輝, 宋美琪, 王毅, 等. 虛擬電容控制下并網型直流微網VSC多約束穩定運行邊界[J]. 電力系統自動化, 2019, 43(15): 172-179, 199.

Meng Jianhui, Song Meiqi, Wang Yi, et al. Multi- constraint stable operation boundary of grid- connected voltage source converter of DC microgrid with virtual capacitance control[J]. Automation of Electric Power Systems, 2019, 43(15): 172-179, 199.

[23] 湯廣福. 基于電壓源換流器的高壓直流輸電技術[M]. 北京: 中國電力出版社, 2010.

[24] 季一潤, 袁志昌, 趙劍鋒, 等. 一種適用于柔性直流配電網的電壓控制策略[J]. 中國電機工程學報, 2016, 36(2): 335-341.

Ji Yirun, Yuan Zhichang, Zhao Jianfeng, et al. A suitable voltage control strategy for DC distribution power network[J]. Proceedings of the CSEE, 2016, 36(2): 335-341.

[25] 曹文遠, 韓民曉, 謝文強, 等. 交直流配電網逆變器并聯控制技術研究現狀分析[J]. 電工技術學報, 2019, 34(20): 4226-4241.

Cao Wenyuan, Han Minxiao, Xie Wenqiang, et al. Analysis on research status of parallel inverters control technologies for AC/DC distribution net- work[J]. Transactions of China Electrotechnical Society, 2019, 34(20): 4226-4241.

[26] 張興, 張崇巍. PWM 整流器及其控制[M]. 北京: 機械工業出版社, 2012.

Quantitative Calculation Method of Bus Voltage Sag Peak Value in Radial DC Distribution Network

（School of Electrical and Information Engineering Changsha University of Science and Technology Changsha 410000 China）

Different from AC distribution network, DC distribution network has low inertia characteristics. When the load of distribution network changes suddenly, DC bus voltage fluctuates greatly, and the quality of bus voltage faces great challenges. In order to solve the problem of low inertia of DC distribution network, super capacitor can be used to increase physical inertia or virtual capacitor (which needs to be provided by redundant capacity of converter configuration) to increase virtual inertia. The larger the capacitance, the higher the quality of power supply, but the higher the cost. However, the research on the suppression effect of capacitor on voltage sag is mainly qualitative analysis and lacks quantitative calculation. Therefore, the transient response of DC bus voltage under sudden load increase in radial DC distribution network is analyzed, and the mathematical relationship between the peak value of bus voltage sag and the DC side capacitance value of tie converter is obtained, which provides theoretical support for the design of system inertia parameters. Due to the complexity of the mathematical relation, a simplified method is designed to obtain the approximate algebraic relation for the convenience of engineering application. Finally, the calculation method of voltage sag peak value is verified by simulation and experiment.

DC distribution network, low inertia characteristics, voltage sag suppression, calculation of voltage sag peak value

10.19595/j.cnki.1000-6753.tces.210846

TM721.1

唐 欣 男，1975年生，教授，博士生導師，研究方向為電力電子在電力系統中的應用。E-mail: tangxin_csu@163.com

蔡明君 男，1993年生，碩士研究生，研究方向為電力電子在電力系統中的應用。E-mail: 656632880@qq.com（通信作者）

國家自然科學基金資助項目（51977013）。

2021-06-14

2022-04-27

（編輯 陳 誠）