考慮磁橋不均勻飽和的內置式永磁同步電機等效磁網絡模型

佟文明 姚穎聰 李世奇 位海洋

考慮磁橋不均勻飽和的內置式永磁同步電機等效磁網絡模型

佟文明 姚穎聰 李世奇 位海洋

（沈陽工業大學國家稀土永磁電機工程技術研究中心 沈陽 110870）

為了提高計算精度，提出了一種可考慮磁橋不均勻飽和的內置式永磁同步電機（IPMSM）改進等效磁網絡（EMN）模型。在分析不均勻飽和現象產生機理的基礎上，將極間磁橋劃分為四個子區域，根據每個子區域的幾何結構及其磁力線走向搭建相應的多段非線性磁導單元，以考慮磁橋不均勻飽和及飽和偏移現象。以一臺20kW車用IPMSM為例，利用所提出的模型對電機的空載、負載磁場及空載反電動勢進行計算，并將計算結果與傳統EMN模型、有限元分析及實驗結果進行對比。結果表明，相比于傳統EMN模型，所提出的改進EMN模型對氣隙磁通密度和空載反電動勢的計算精度可提高4%以上。最后，分析所提出模型的適用性，結果表明，當磁橋內磁通密度最大值與最小值的比大于約1.3時，磁橋不均勻飽和現象嚴重，需通過所提出的改進EMN模型來準確計算電機的電磁特性。

內置式永磁同步電機 等效磁網絡法 磁橋不均勻飽和 有限元分析

0 引言

內置式永磁（Interior Permanent Magnet, IPM）電機憑借其高轉矩密度、寬恒功率運行區、低永磁體渦流損耗等特點，在混合動力汽車和純電動汽車領域得到了廣泛的應用[1-3]。精確的磁場計算是預測電機性能和判斷其設計合理性的前提。目前，常用的電機磁場分析方法包括解析法、等效磁網絡（Equivalent Magnetic Network, EMN）法和有限元分析（Finite Element Analysis, FEA）法。

由于IPM電機的轉子結構復雜，其邊界條件難以確定，因此很難直接采用基于麥克斯韋方程的解析法計算此類電機的磁場分布。采用FEA法雖可以精確地獲得電機磁場分布，但由于IPM電機轉子結構的多樣性以及軟件對網格數量的要求，導致該方法計算時間較長，不利于電機的初始設計[4]。EMN法由于具有計算速度較快且精度適中的特點，近年來受到眾多學者的關注[5-15]。

文獻[6]針對磁通切換永磁電機建立一種考慮電機負載時定子軛部與齒部之間漏磁的EMN模型。文獻[7-8]分別建立了磁通反向直線旋轉永磁電機和軸向磁通永磁同步電機的三維EMN模型，通過與FEA對比，三維EMN模型在保證計算精度的情況下，計算速度顯著提升。文獻[9-10]分別針對車載雙永磁游標電機和表貼式永磁同步電機建立了EMN模型，兩者都采用了一種菱形網格單元來進行局部建模以提高模型的計算精度。在IPM電機領域，文獻[11]提出了一種U型IPM電機的動態EMN模型。文獻[12]針對三層三段IPM電機提出了一種考慮轉子交叉耦合效應的EMN模型。文獻[13]針對非對稱轉子IPM電機建立了一種考慮磁橋端部漏磁的EMN模型。文獻[14]針對IPM電機提出了一種結合了精確保角映射的EMN模型。文獻[15]針對IPM電機提出了一種EMN模型，該模型采用十字形磁導對氣隙進行建模來提高計算精度。然而，上述IPM電機的EMN模型雖能較為準確地計算出電機空載時氣隙磁通密度幅值處的波形，但由于模型在極間磁橋區域的磁導建模較為簡單，無法準確考慮到磁橋區域存在的不均勻飽和現象，導致計算出的磁橋正對氣隙區域的磁通密度波形與實際情況存在誤差；在IPM電機負載情況下，不均勻飽和現象會更加嚴重，同時還會伴隨著磁橋飽和偏移的發生，這會進一步加大計算誤差。

針對該問題，本文提出一種考慮磁橋不均勻飽和以及飽和偏移的改進磁網絡模型。通過分析不均勻飽和現象產生的原因，將極間磁橋劃分為四個子區域，并對各自區域建立多段十字形磁導以考慮交叉耦合的影響。為了驗證該模型，本文以一臺20kW車用V型IPM電機為例，通過所提出的模型對電機的空載磁場、負載磁場及空載反電動勢進行計算，并將計算結果與傳統EMN模型、FEA及實驗結果進行對比。此外，本文通過改變電機的磁橋結構，還對該模型的適用性進行分析。

1 不均勻飽和極間磁橋的分析

以V型IPM電機為例，本文將轉子中包含異性磁極間漏磁通的區域統稱為極間磁橋區域，圖1所示為V型IPM電機的拓撲結構。電機額定負載下的有限元仿真結果及磁橋區域劃分如圖2所示，根據極間磁橋區域的幾何結構及磁通密度分布情況，將極間磁橋劃分為4個子區域，可以看出，不均勻飽和現象主要存在于區域2和3。

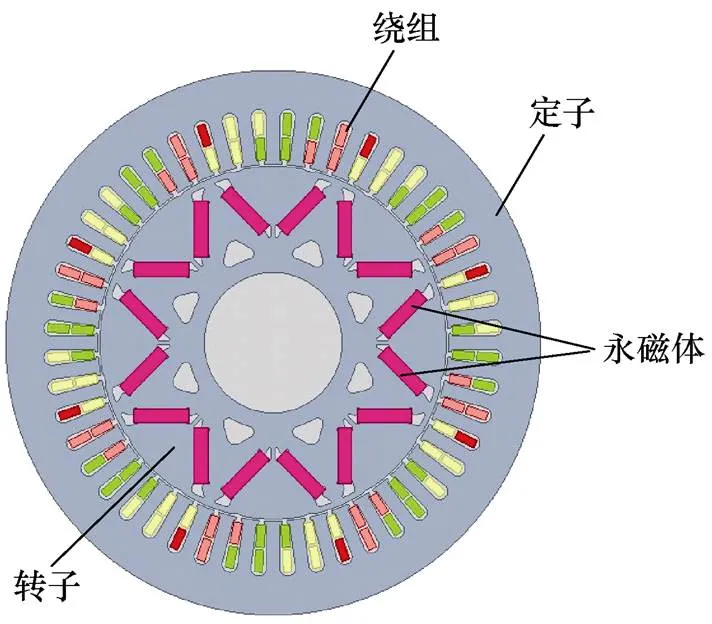
圖1 V型內置式永磁電機拓撲結構

為了考慮磁橋的不均勻飽和，本文對極間磁橋區域提出如圖3所示的EMN建模方法。對于區域1，由于其飽和程度通常較低，磁通密度分布較為均勻，故將此區域磁導等效為一段圓弧形的磁導。對于區域2，其磁通密度分布主要受幾何結構的影響，越接近區域3的位置，磁通路徑越窄，進而磁通密度越大。同時，根據磁力線走向可以看出，該區域還存在一部分直接進入氣隙的磁力線。出于對以上兩種情況的考慮，本文將區域2分為多個近似梯形的磁導單元，并在每個單元中建立十字形磁導，在考慮該區域幾何結構變化的同時也為磁通提供了流入氣隙路徑。

圖2 內置式永磁同步電機磁通密度云圖及磁橋區域劃分

圖3 極間磁橋區域的磁導模型

區域2的磁通密度分布呈現出一種遞增的變化趨勢，并在與區域3的交界處達到最大值。同時根據磁力線走向可以看出，在區域3中，同樣存在大量進入氣隙的磁力線，導致等寬的磁橋內部磁通密度也在不斷變化，故區域3仍然存在較為明顯的不均勻飽和現象。本文將區域3分為多個矩形磁導單元，并在每個單元中建立十字形磁導，為從該區域進入氣隙的磁通提供了流通路徑。對于區域4，由于其磁通密度分布較為均勻，故將此區域簡化為一個矩形磁導單元，并建立十字形磁導。

對于圖3所示的磁網絡模型，建立的十字形磁導的數目越多，氣隙磁通密度的計算結果越精確。但磁導數目增加的同時也會導致計算量的增加，并且當磁導數目增加到一定值后，氣隙磁通密度的計算精度將不會產生明顯的提升。經過多次嘗試，本文最終將極間磁橋區域的磁導單元數目確定為15個。需要注意的是，為了方便后續轉子EMN模型和氣隙EMN模型的組合，需要保證圖3中磁導單元的寬度盡可能相同。

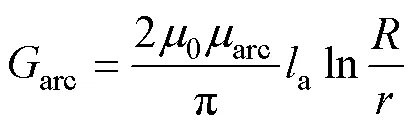
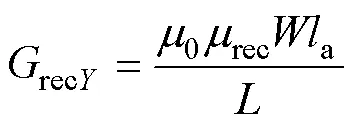
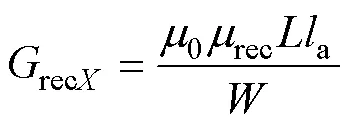
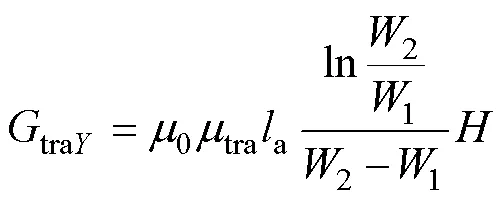
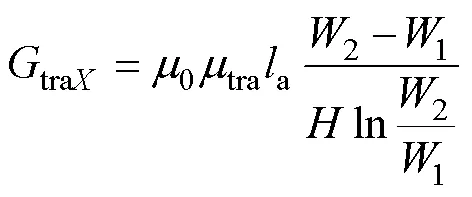
式中，0為真空磁導率；arc為圓弧形磁導的相對磁導率；和分別為圓弧形磁導對應磁通路徑的外半徑和內半徑；rec為矩形磁導的相對磁導率；a為電機軸向長度；和分別為矩形磁導對應磁通路徑的長度和寬度；tra為梯形磁導的相對磁導率；1、2和分別為梯形磁導對應磁通路徑的上底、下底長度和高度。

2 等效磁網絡模型的建立及求解

2.1 等效磁網絡模型的建立

定子等效磁網絡模型如圖4所示。其中，包含齒部磁導、軛部磁導、槽漏磁導及電樞繞組等效磁動勢源。考慮到定子齒尖局部飽和，在每個齒的齒頂部位加入了兩個非線性磁導。圖4中，磁導的值可以通過式（2）進行計算，由分布繞組產生的磁動勢可表示為與軛部磁導相串聯的磁動勢源，其值為

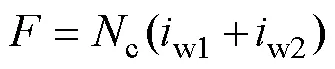
式中，c為槽內每個線圈的匝數；w1和w2為槽內電樞繞組所通的電流。

氣隙區域的EMC模型由兩種磁導組成，分別是氣隙磁導和槽口磁導。氣隙區域可以被劃分為多層矩形磁導單元，并在每個單元中建立十字形磁導，如圖5a所示。文獻[15]中提出，氣隙磁導單元層數的增加對氣隙磁通密度計算精度的改善較為有限。因此，綜合考慮模型計算精度與計算時間，本文氣隙磁導單元的層數選為1。槽口區域可以近似等效為兩段圓弧型磁導單元，如圖5b所示。圖5中所有的氣隙磁導值可由式（1）～式（3）計算得到。

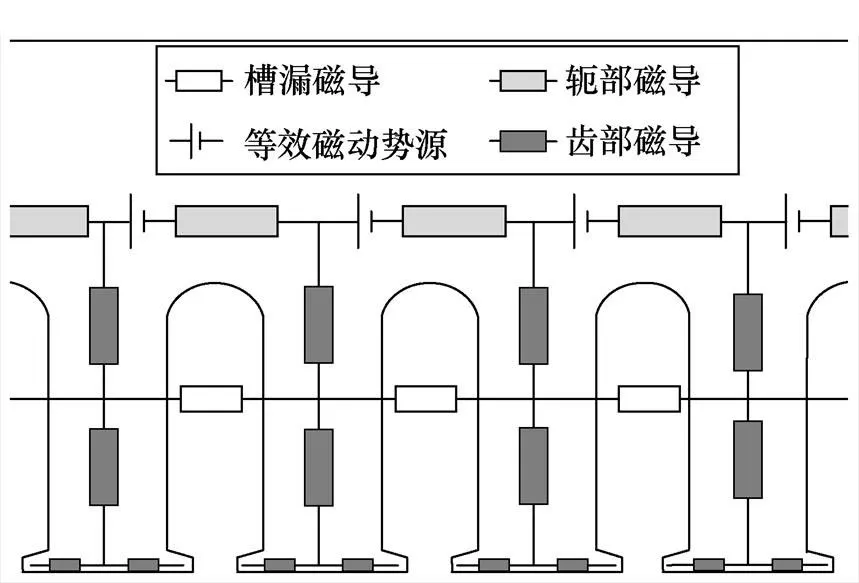
圖4 定子等效磁網絡模型

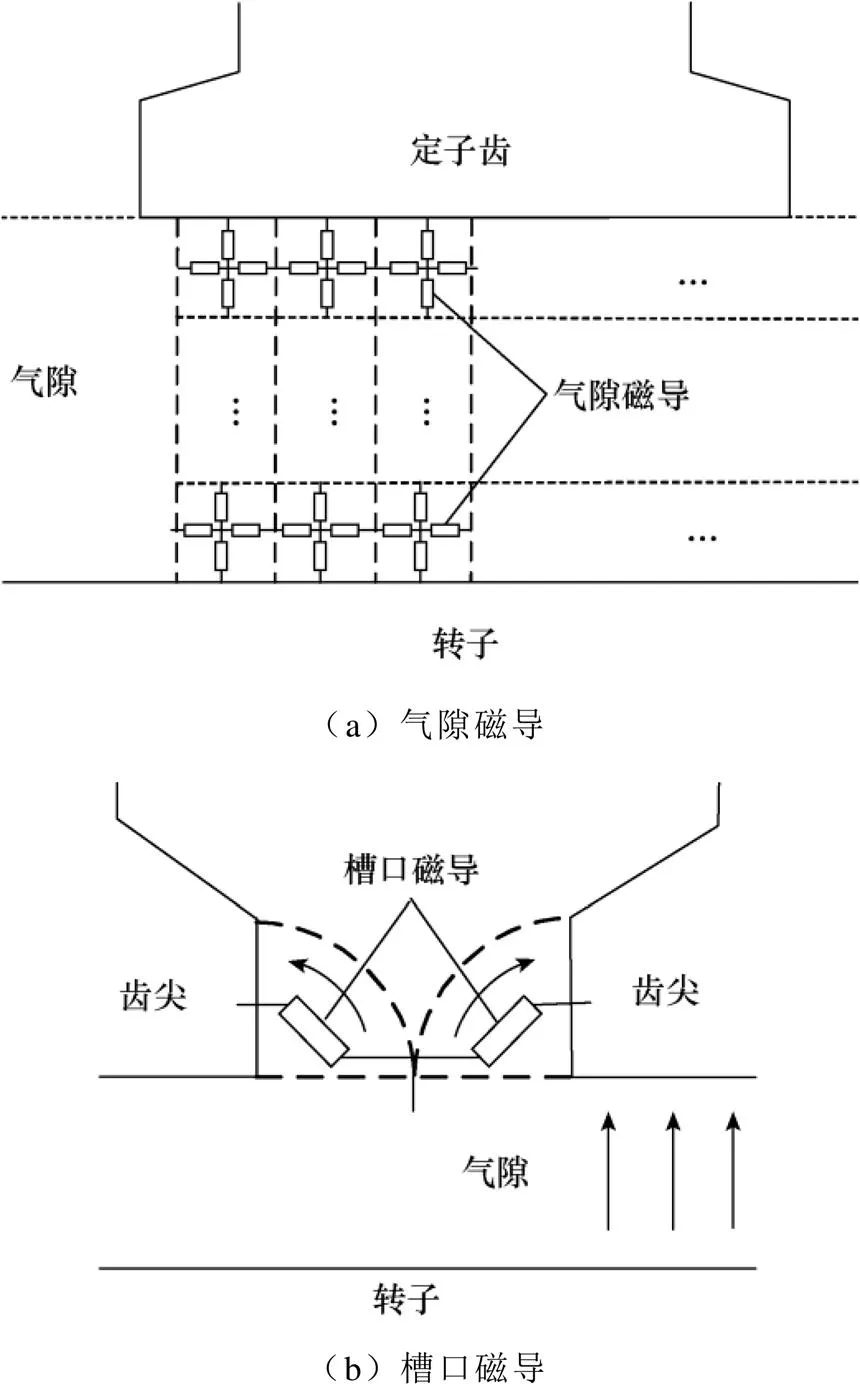
圖5 氣隙等效磁網絡模型

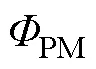
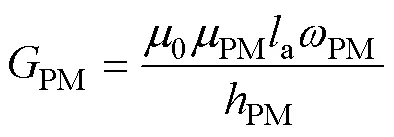
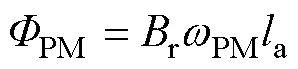
式中，PM為永磁材料相對磁導率；PM和PM分別為永磁體的寬度和厚度；r為永磁體剩磁。

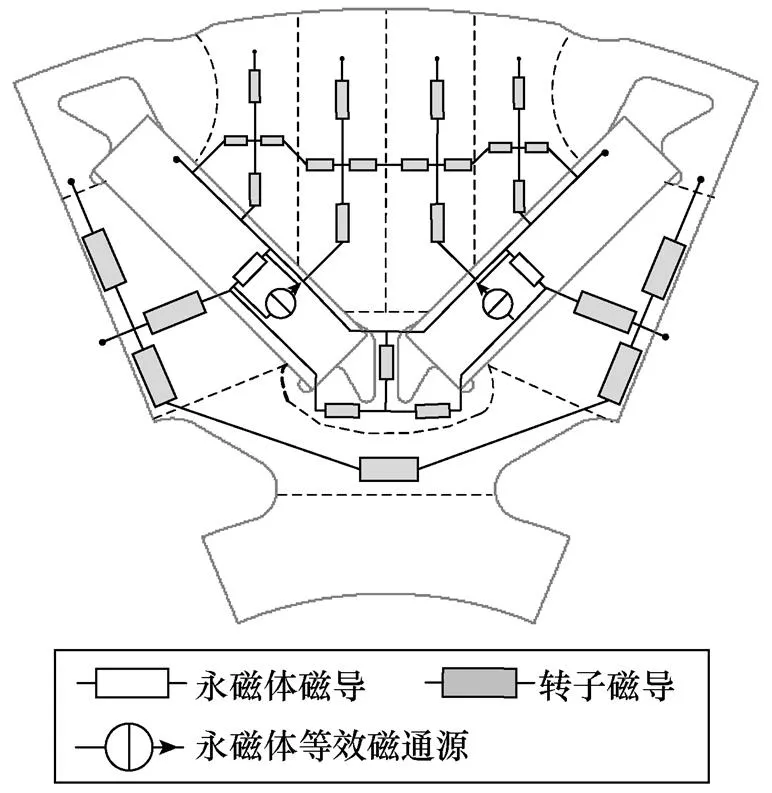
圖6 轉子除極間磁橋區域外的等效磁路模型

考慮不均勻飽和前后的極間磁橋區域EMN模型如圖7所示。兩種模型都包含有永磁體漏磁導和磁橋磁導。改進EMN模型中可連接氣隙磁導的節點明顯多于傳統EMN模型。即考慮不均勻飽和的EMN模型所提供的流入氣隙磁通路徑更多，更能反映電機在極間磁橋區域的實際磁通走向，進而可提高計算精度。圖7中所有的磁導都可以通過式（1）～式（5）得到。

2.2 非線性磁導的求解

非線性磁導相對磁導率需要通過迭代求得。首先，根據轉子位置確定完整的EMN模型，并設置非線性磁導相對磁導率為，通過計算出每條支路的磁導。與電路中的節點電壓方程類似，EMN模型的節點磁動勢矩陣為

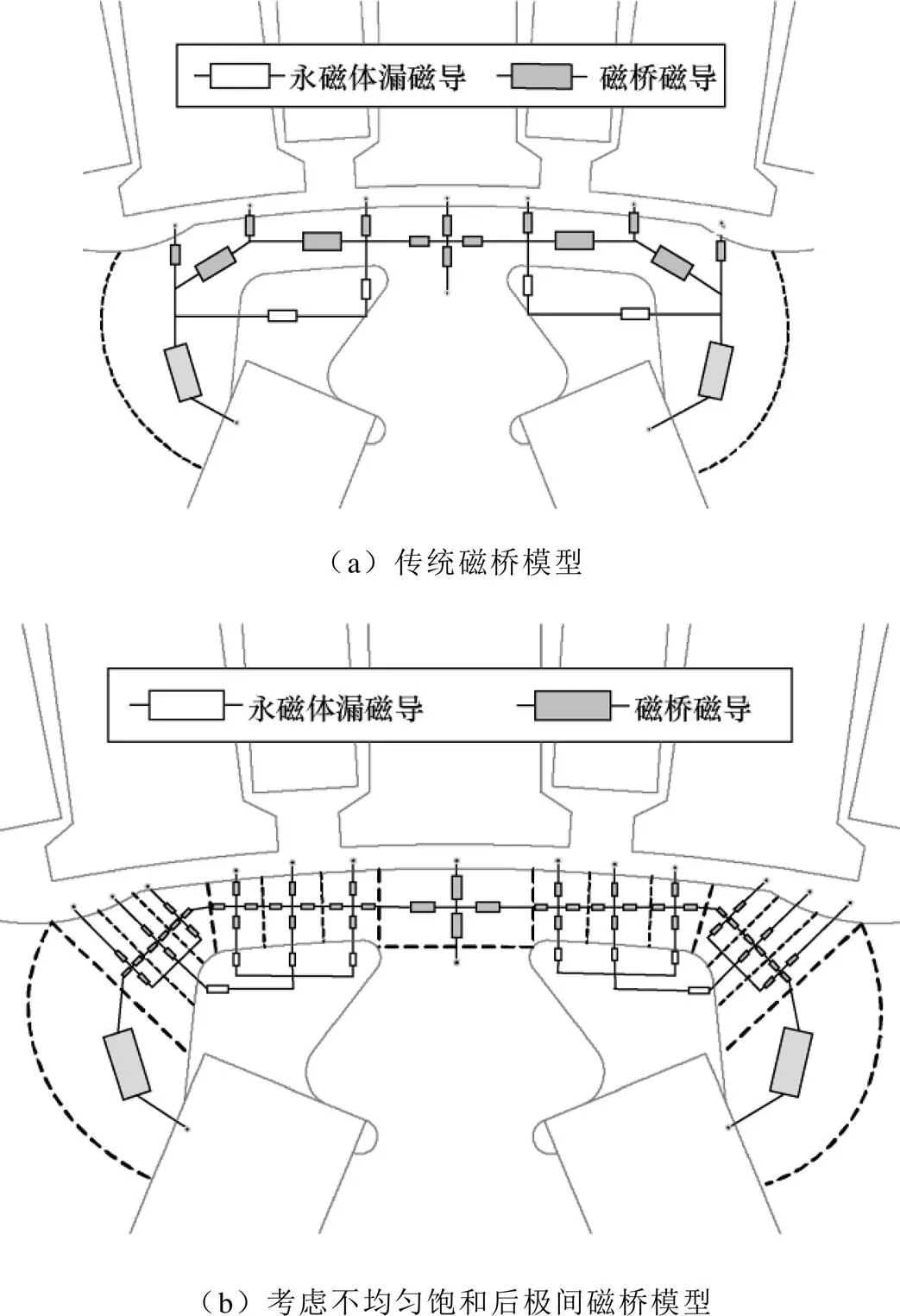
圖7 極間磁橋區域等效磁路模型

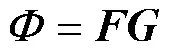
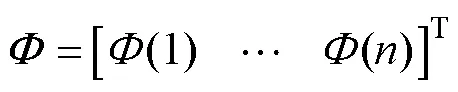
其中，磁導矩陣具有以下特性

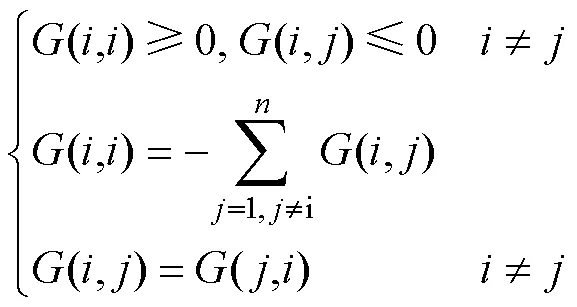
在求得節點磁動勢矩陣后，各支路磁導所對應的磁通密度e為

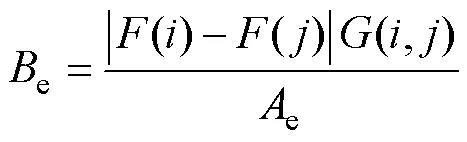
式中，e為與兩節點之間磁通經過的截面積。

計算得到的e后，在查找鐵磁材料的-曲線后便可以得到相對磁導率+1。為了加快迭代循環的計算速度，磁導率更新迭代公式[16]為

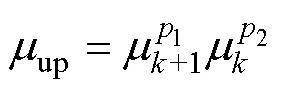
式中，1=0.95；2=0.05；up為更新后的相對磁導率。

迭代過程的終止條件是磁導率收斂到設定的誤差范圍內，該條件可以表示為

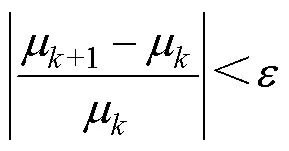
當某個轉子位置的循環結束后，調整節點連接順序，更換新的轉子位置重新進行循環，直到完成所有位置的計算。非線性磁導求解流程如圖8所示。

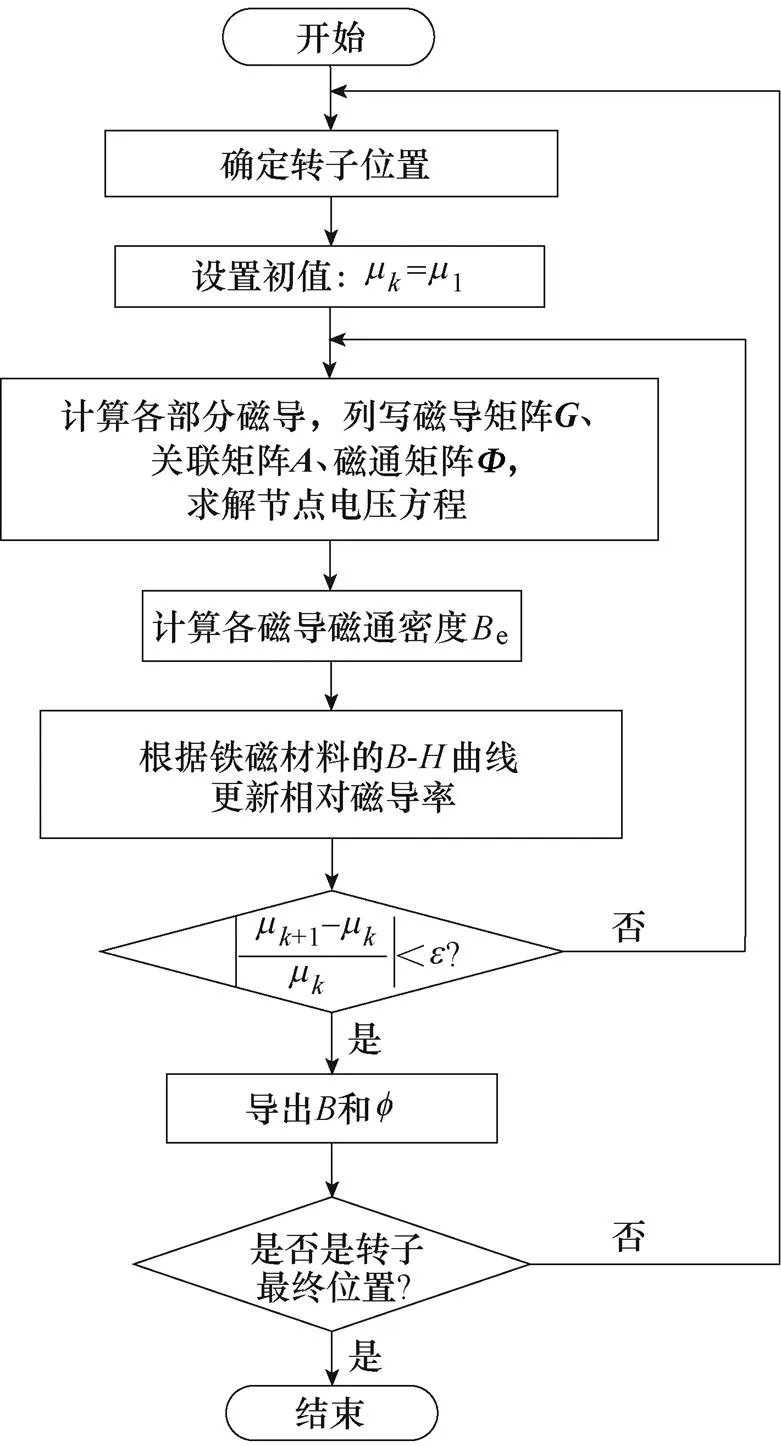
圖8 非線性磁導求解流程

3 不均勻飽和磁橋模型的驗證

為了驗證所提出模型的有效性，本文分別用考慮磁橋不均勻飽和前后的兩種EMN模型對一臺V型IPM電機進行了計算，并將結果與FEA及實驗結果進行對比。其中，樣機結構及測試平臺如圖9所示，電機主要參數見表1。為了區分兩種模型的計算結果，本文將改進EMN模型表示為EMN1，傳統EMN模型表示為EMN2。

圖9 樣機圖片及實驗平臺

表1 內置式永磁同步電機參數

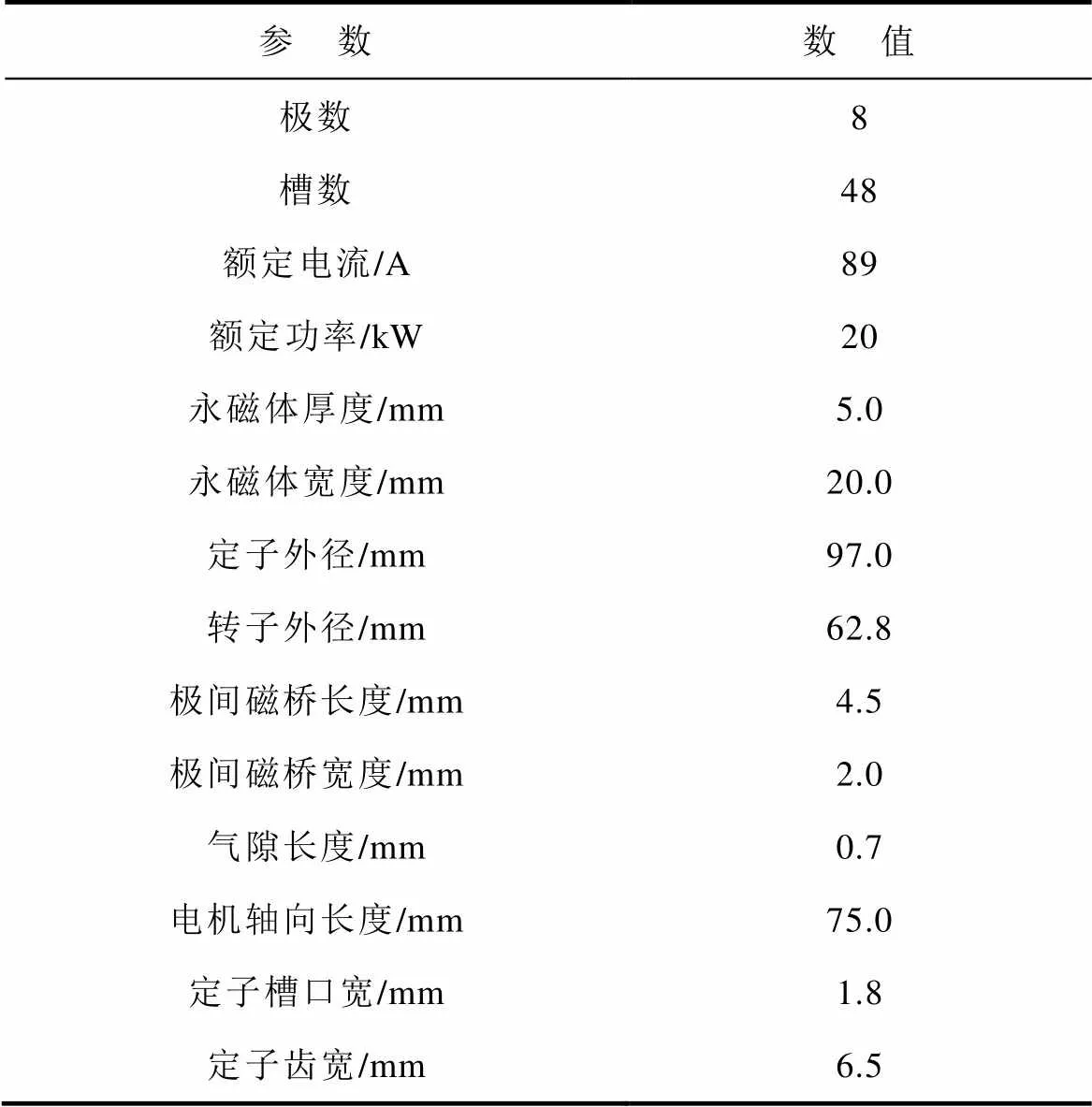
Tab.1 IPM machine parameters

3.1 空載氣隙磁通密度波形對比

不同定、轉子相對位置時空載氣隙磁通密度波形如圖10所示，圖中，位置1表示轉子d軸正對于定子齒中央；位置2表示轉子d軸正對于定子槽中央。可以看出，EMN2模型在氣隙磁通密度波形幅值處的計算結果與FEA結果吻合較好，而在點畫線范圍內極間磁橋正對的氣隙磁通密度波形與FEA結果存在明顯偏差。對于EMN1模型而言，整體氣隙磁通密度波形與FEA結果吻合良好。為了對比磁網絡結果與FEA結果間的差別，對氣隙磁通密度進行誤差分析，有

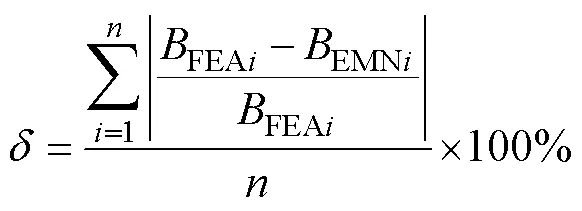
式中，BEMNi為EMN模型第i個磁導處的氣隙磁通密度；BFEAi為與EMN模型第i個磁導相同周向位置處的FEA計算磁通密度；n為EMN模型中的氣隙磁導單元數目。

通過計算得到，位置1處EMN1、EMN2計算結果與FEA結果的誤差分別為2.14%和6.64%；位置2處EMN1、EMN2計算結果與FEA結果的誤差分別為3.36%和8.09%。可以看出，EMN1模型計算結果具有更高的精度，尤其對于圖10中點畫線范圍內的氣隙磁通密度過零處，波形計算結果得到了明顯的改善，這表明改進EMN模型可有效考慮磁橋不均勻飽和的影響。

3.2 負載氣隙磁通密度波形對比

圖11所示為電機負載情況下，不同電流相位時的氣隙磁通密度的計算值，此時電流有效值為89A。通過計算得到，當相位為0°時，EMN1、EMN2計算結果與FEA結果的誤差分別為5.54%和10.71%；相位為45°時，EMN1、EMN2計算結果與FEA結果的誤差分別為5.31%和10.18%。可以看出，負載時受磁橋不均勻飽和以及磁橋飽和偏移的影響，EMN2模型的計算結果與FEA結果誤差更為顯著，但EMN1模型的計算結果仍與FEA結果吻合性較好，尤其對于圖11中點畫線范圍內的極間磁橋區域正對的氣隙磁通密度處，波形計算結果得到了明顯的改善，這表明改進EMN模型可有效考慮電機在負載情況下磁橋不均勻飽和以及飽和偏移的影響。

圖11 不同電流相位下的氣隙磁通密度波形

此外，與空載氣隙磁通密度計算結果相比，在負載情況下受磁橋飽和偏移的影響，改進EMN模型的計算精度有所下降，可以通過適當增加磁橋中磁導單元的數目來提高負載情況下的計算精度。

3.3 空載反電動勢波形對比

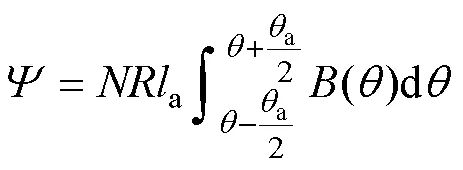
式中，為該相繞組的匝數；為氣隙處半徑；為轉子的位置角；為一個線圈的節距角。

計算得到該電機的磁鏈波形如圖12所示。通過磁鏈波形，可以計算得到IPM電機的空載反電動勢，即

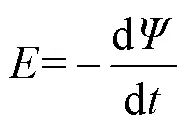
圖13所示為兩種EMN模型計算的空載反電動勢波形與有限元及實驗的對比結果，其中空載反電動勢的實測波形如圖14所示。通過計算得到EMN1、EMN2計算結果與實驗結果的誤差分別為5.23%和10.35%，該結果進一步表明了改進EMN模型擁有更高計算精度。

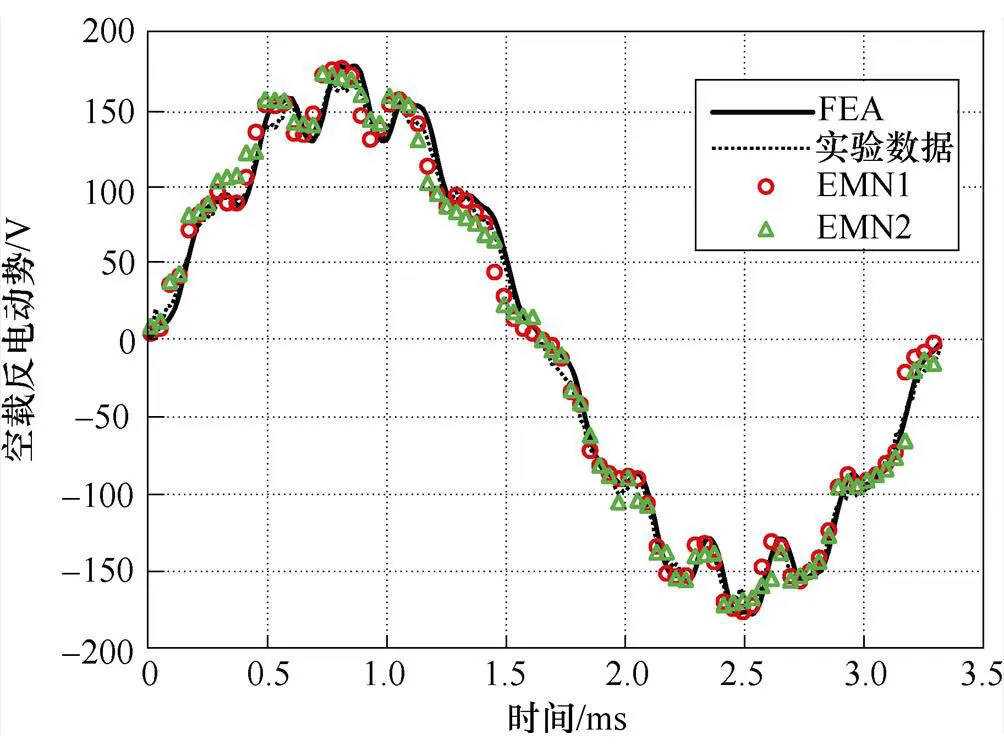
圖13 空載反電動勢波形對比

圖14 空載反電動勢測試結果

4 模型適用性分析

為了總結所提出模型的適用條件，本文對不同磁橋尺寸下的電機氣隙磁通密度進行了分析，如圖15所示。保證磁橋長度為4.5mm不變，只改變磁橋寬度時兩種EMN模型的空載氣隙磁通密度的計算結果如圖15a所示，圖中，2mm、2.5mm和3mm為磁橋的寬度。保證磁橋寬度為2mm不變，只改變磁橋長度時兩種EMN模型的空載氣隙磁通密度的計算結果如圖15b所示，圖中，3mm、4.5mm和6mm為磁橋的長度。通過式（17）計算得到不同磁橋尺寸下兩種模型對氣隙磁通密度的計算結果與FEA結果的誤差見表2。

由表2可以看出，不同磁橋尺寸對兩種模型的計算精度有一定影響，即磁橋尺寸的改變引起了磁橋內部不均勻飽和程度的改變。為了驗證模型的適用性，本文以IPM電機極間磁橋內部磁通密度最大值與最小值的比值來表示該磁橋的不均勻飽和程度。圖16所示為不同磁橋尺寸下磁橋內部的磁通密度變化曲線，以長為4.5mm，寬為2mm的磁橋為例，圖16中橫坐標對應的磁橋位置如圖17所示。不同磁橋尺寸下磁橋內部磁通密度的比值見表2。

圖15 不同磁橋尺寸下電機的氣隙磁通密度波形

表2 不同磁橋尺寸兩種模型計算誤差對比

Tab.2 Calculation errors of two models at different bridge sizes

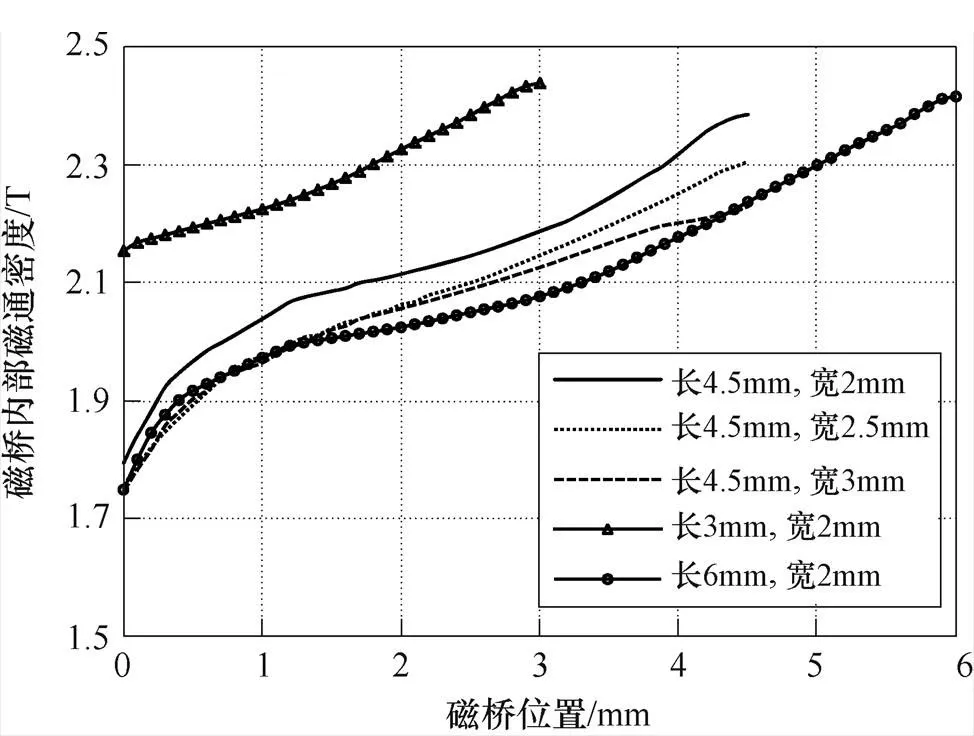
圖16 不同磁橋尺寸下磁橋內部的磁通密度變化

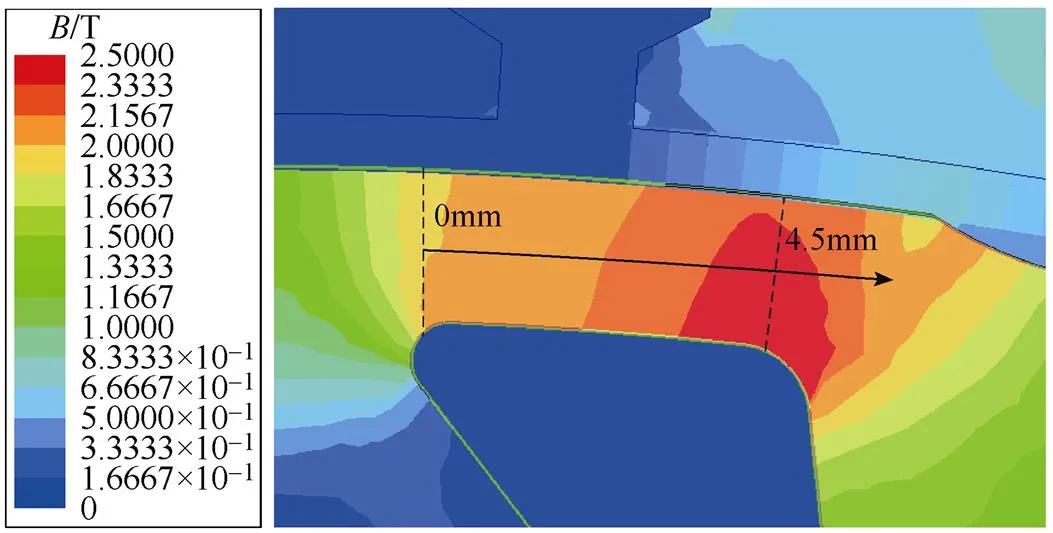
圖17 圖16中橫坐標所對應的磁橋位置

通過計算，當磁橋內磁通密度最大值與最小值的比小于約1.30時，兩種模型的計算誤差都可以控制在6%以內，此時采用擁有較少磁導數目的傳統EMN模型更為適合；當磁橋內磁通密度最大值與最小值的比大于約1.30時，磁橋不均勻飽和現象嚴重，傳統EMN模型的計算誤差較大，需要通過所提出的改進EMN模型來準確計算電機磁場分布。

5 結論

本文針對IPM電機提出了一種能夠考慮磁橋不均勻飽和的建模方法。用該方法建立的車用IPM電機EMN模型能夠考慮電機轉子中存在的極間磁橋不均勻飽和現象以及負載時的飽和偏移現象。

為了驗證該方法，本文以一臺20kW車用V型IPM電機為例，通過所提模型對電機的空載磁場、負載磁場及空載反電動勢進行了計算，并將計算結果與傳統EMN模型、有限元分析及實驗結果進行了對比。通過誤差分析的結果表明，相較于傳統的EMN模型，改進EMN模型對氣隙磁通密度波形的計算精度可提高4%以上，對空載反電動勢的計算精度可提高5%以上。

最后，本文還對所提出模型的適用性進行了分析，結果表明，對于磁橋內磁通密度最大值與最小值的比小于約1.30的IPM電機，本文所提出模型計算精度與傳統EMN模型相當，此時采用擁有較少磁導數目的傳統EMN模型更為適合；當磁橋內磁通密度最大值與最小值的比大于約1.30時，磁橋不均勻飽和現象嚴重，需要通過所提出的改進EMN模型來準確計算電機磁場分布。

[1] 唐任遠. 現代永磁電機理論與設計[M]. 北京: 機械工業出版社, 2006.

[2] 馬偉明, 王東, 程思為, 等. 高性能電機系統的共性基礎科學問題與技術發展前沿[J]. 中國電機工程學報, 2016, 36(8): 2025-2035.

Ma Weiming, Wang Dong, Cheng Siwei, et al. Com- mon basic scientific problems and development of leading-edge technology of high performance motor system[J]. Proceedings of The CSEE, 2016, 36(8): 2025-2035.

[3] 樊英, 譚超. 內置式交替極永磁同步電機性能及機理研究[J]. 電工技術學報, 2018, 33(11): 2414-2422.

Fan Ying, Tan Chao. Analysis of electromagnetic performance and principles in inserted consequent- pole permanent magnet synchronous machines[J]. Transactions of China Electrotechnical Society, 2018, 33(11): 2414-2422.

[4] Wu Shuang, Shi Tingna, Guo Liyan, et al. Accurate analytical method for magnetic field calculation of interior PM motors[J]. IEEE Transactions on Energy Conversion, 2020, 36(1): 325-337.

[5] Yang Shuo, Salim A, Sami H, et al. Introduction to mesh based generated lumped parameter models for electromagnetic problems[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(2): 152-162.

[6] 張淦, 花為, 程明, 等. 磁通切換型永磁電機非線性磁網絡分析[J]. 電工技術學報, 2015, 30(2): 34-42.

Zhang Gan, Hua Wei, Cheng Ming, et al. Analysis of nonlinear magnetic network models for flux- switching permanent magnet machines[J]. Transa- ctions of China Electrotechnical Society, 2015, 30(2): 34-42.

[7] 郭凱凱, 郭有光. 磁通反向直線旋轉永磁電機三維非線性等效磁路模型分析[J]. 電工技術學報, 2020, 35(20): 4278-4286.

Guo Kaikai, Guo Youguang. 3D Nonlinear equivalent magnetic circuit model analysis of a flux reversal linear rotary permanent magnet machine[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(20): 4278-4286.

[8] He Mingjie, Li Weiye, Peng Jun, et al. Multi-layer quasi three-dimensional equivalent model of axial- flux permanent magnet synchronous machine[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(1): 3-12.

[9] Cao Donghui, Zhao Wenxiang, Ji Jinghua, et al. A generalized equivalent magnetic network modeling method for vehicular dual-permanent-magnet vernier machines[J]. IEEE Transactions on Energy Conversion, 2019, 34(4): 1950-1962.

[10] Cao Donghui, Zhao Wenxiang, Ji Jinghua, et al. Parametric equivalent magnetic network modeling approach for multiobjective optimization of PM machine[J]. IEEE Transactions on Industrial Elec- tronics, 2021, 68(8): 6619-6629.

[11] 陳威, 吳桂初, 方攸同. 基于繞組分布函數理論和動態磁網絡的兩種內置式永磁牽引電機解析建模方法[J]. 電工技術學報, 2020, 35(增刊2): 377-386.

Chen Wei, Wu Guichu, Fang Youtong. Two analytical models based on winding function theory and dynamic reluctance mesh for interior permanent magnet traction machines[J]. Transactions of China Electrotechnical Society, 2020, 35(S2): 377-386.

[12] Zhu Li, Jiang Shuzhong, Zhu Ziqiang, et al. Analytical modeling of multi-segment and multilayer interior permanent magnet machines[C]//2014 17th International Conference on Electrical Machines and Systems (ICEMS), Hangzhou, 2014: 28-33.

[13] Xu Gaohong, Liu Guohai, Jiang Shan, et al. Analysis of a hybrid rotor permanent magnet motor based on equivalent magnetic network[J]. IEEE Transactions on Magnetics, 2018, 54(4): 1-9.

[14] Li Zhaokai, Huang Xiaoyan, Wu Lijian, et al. Open- circuit field prediction of interior permanent-magnet motor using hybrid field model accounting for saturation[J]. IEEE Transactions on Magnetics, 2019, 55(7): 1-7.

[15] Liu Guohai, Wang Yong, Chen Qian, et al. Design and analysis of a new equivalent magnetic network model for IPM machines[J]. IEEE Transactions on Magnetics, 2020, 56(6): 1-12.

[16] Tong Wenming, Wang Shuai, Dai Shanhong, et al. A quasi-three-dimensional magnetic equivalent circuit model of a double-sided axial flux permanent magnet machine considering local saturation[J]. IEEE Transa- ctions on Energy Conversion, 2018, 33(4): 2163- 2173.

Equivalent Magnetic Network Model for Interior Permanent Magnet Machines Considering Non-Uniform Saturation of Magnetic Bridges

（National Engineering Research Center for Rare-Earth Permanent Magnet Machines Shenyang University of Technology Shenyang 110870 China）

In order to improve the calculation accuracy, an improved equivalent magnetic network (EMN) model is proposed for interior permanent magnet synchronous motors (IPMSM) considering the non-uniform saturation of the magnetic bridge. By analyzing the causes of uneven saturation phenomenon, the magnetic bridge is divided into four regions. According to the geometric structure and flux distribution of each region, the nonlinear permeance unit is used to consider the non-uniform saturation and the saturation shift of the magnetic bridge. Then, taking a 20kW IPMSM as an example, the proposed model is used to analyze the no-load and load magnetic fields and no-load back electromotive force (EMF), and the calculated results are compared with the traditional EMN model, finite element analysis (FEA) and experimental results. It is shown that the proposed model can improve the calculation accuracy by more than 4% compared with the traditional EMN model. Finally, the applicability of the proposed model is analyzed. The results show that when the ratio of the maximum to minimum magnetic density in the magnetic bridge is greater than about 1.3, it is necessary to consider the non-uniform saturation of the magnetic bridge by the proposed model.

Interior permanent magnet synchronous motor, equivalent magnetic network, non- uniform saturation of bridge, finite element analysis

10.19595/j.cnki.1000-6753.tces.210491

TM351

遼寧省“興遼英才計劃”（XLYC2007107）、國家重點研發計劃（2016YFB0300503）和遼寧省百千萬人才工程資助項目。

2021-04-13

2021-06-25

佟文明 男，1984 年生，博士，教授，博士生導師，研究方向為特種電機及其控制與電機多物理場仿真分析。E-mail: twm822@126.com（通信作者）

姚穎聰 男，1997年生，碩士研究生，研究方向為基于集總參數法的內置式永磁同步電機電磁和熱研究。E-mail: 463440276@qq.com

（編輯 崔文靜）