圖的覆蓋數與分子的凱庫勒結構

胡啟明，許 歡，袁曉彤

(合肥幼兒師范高等專科學校公共教學部，安徽 合肥 230013)

0 引言

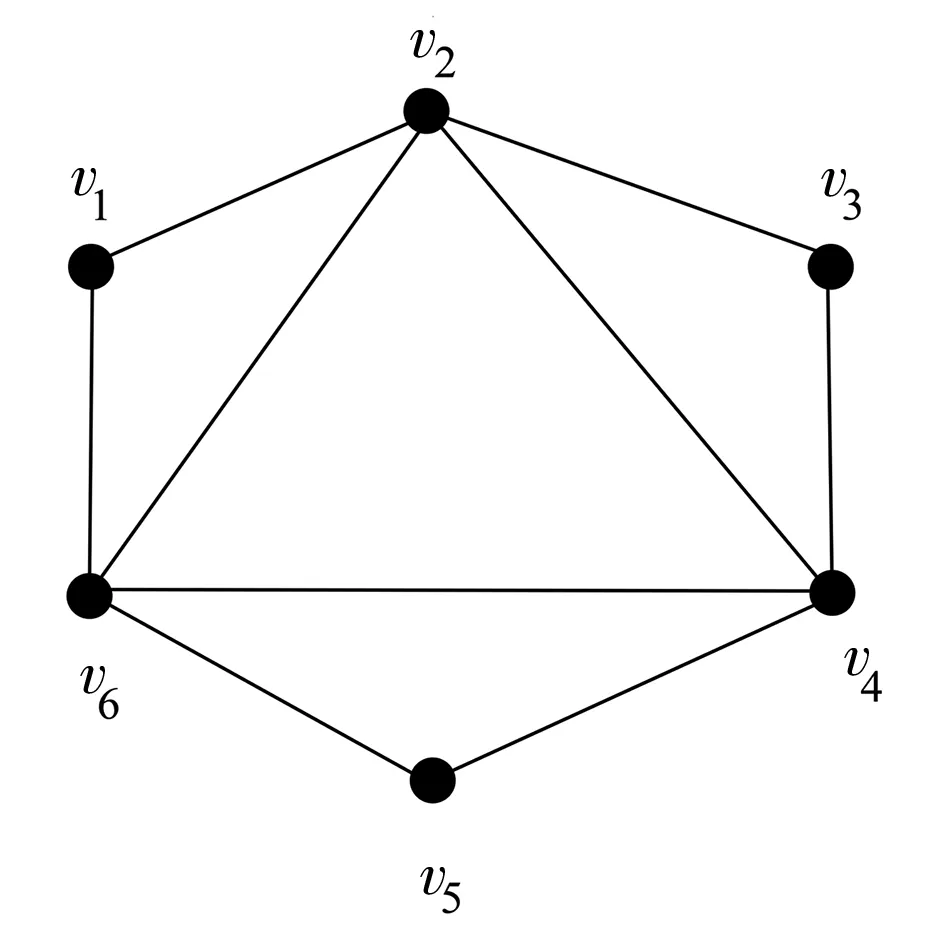
圖1 G1

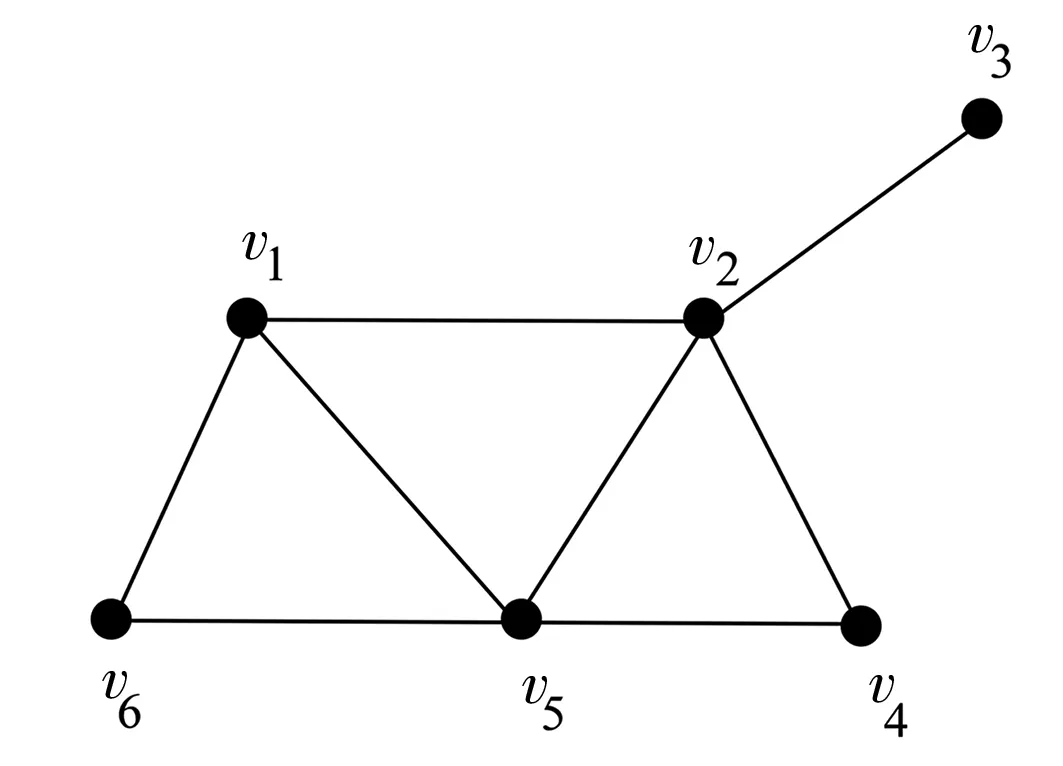
圖2 G2

求圖的最小頂點覆蓋被稱為頂點覆蓋問題(vertex cover problem，VCP)，VCP是理論計算機科學和離散數學中一個經典NP完全問題，可追溯到20世紀30年代Konig的經典結果[1].1972年KARP[2]證明了VCP對于一般圖是NP完全的.求圖的最小邊覆蓋被稱為邊覆蓋問題，該問題是由RABIN[3]首先提出的.邊覆蓋在交通相位問題中起著重要的作用，可應用于網絡分析.到目前為止，只有Mangoldt圖得到了最小邊覆蓋[4].

不失一般性，將化學分子結構看成一個圖，其頂點對應于化合物的原子，邊對應于隱藏于化合物中的化學鍵，稱之為化學圖.多數情況下，化學圖的頂點度都小于或等于4.化學圖論是數學化學的一個分支，化學圖論模型已被廣泛應用于預測化合物的性質[5].在過去幾十年里，學者們對化合物凱庫勒結構的研究積累了許多成果[6-7].

有凱庫勒結構的化學分子，相當于含有完美匹配的化學圖[8].若一個圖含有完美匹配，則稱它為凱庫勒圖.從圖論觀點看，凱庫勒圖是一個有趣問題，如果不分析覆蓋數，這個問題將是未知的.部分學者對凱庫勒結構進行了大量的研究[7-8]，但尚沒有將覆蓋數與凱庫勒結構聯系在一起的研究.在化學圖中，使覆蓋問題有意義的，是它與凱庫勒結構的緊密聯系.因此，本文將討論圖的覆蓋問題，并用覆蓋數刻畫感興趣的化學圖，通過計算一些特殊圖的點覆蓋數和邊覆蓋數，來刻畫覆蓋數和凱庫勒結構的相關性.

1 凱庫勒圖的充要條件

定理1.1 設G=(V,E)是二部圖，則圖G是一個凱庫勒圖?β(G)=β′(G).

證明 “?”假設圖G是一個凱庫勒圖.

“?”假設β(G)=β′(G).

2 因子臨界圖

近似完美匹配，是指圖中存在只剩下一個頂點未被包含的最大匹配.若對于圖中每個頂點都有一個近似完美匹配，則稱該圖為因子臨界圖.也就是說，如果去掉因子臨界圖中的任何一個頂點，它就變成了凱庫勒圖.

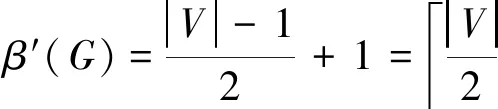
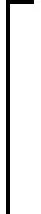
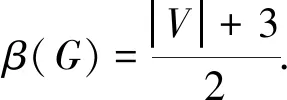
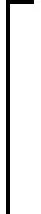
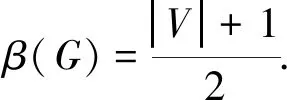
3 頂部梯狀圖

如圖3所示，把頂部梯狀圖記為TLn，n≥0，它們有頂端a和基對b1,b2，與頂端a相鄰的兩條邊稱為圖的頂部，連接基對的邊稱為圖的底部，由底部向下添加梯級(2個頂點、3條邊)構成梯形圖.

例如，TL0(即完全圖K3)可指定其任一個頂點為頂端，其余兩個頂點為基對；又如，TL1(類似于房屋圖)是一個含有5個頂點和6條邊的簡單圖.一般地，任一頂部梯狀圖TLn，n≥0，都有2n+3個頂點和3(n+1)條邊.這類圖包含近似完美匹配，即頂部梯狀圖都是因子臨界圖.

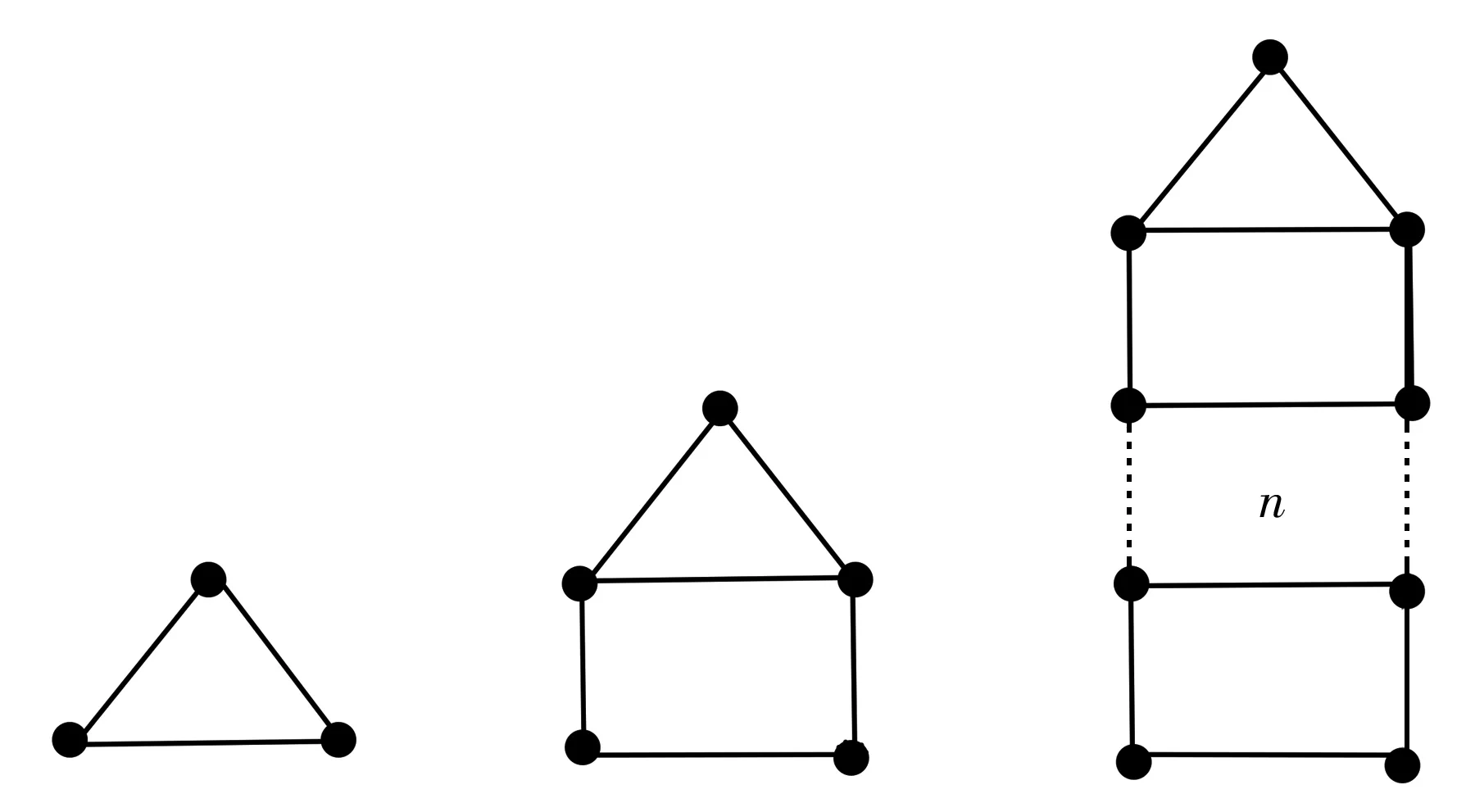
(a)TL0 (b)TL1 (c)TLn圖3 頂部梯狀圖

定理3.1 若G是一個頂部梯狀圖TLn，則β(G)=n+2，n≥0.

證明 用數學歸納法，

當n=0時，G為TL0是K3，此時，β(G)=β(TL0)=2=0+2；

當n=1時，G為TL1是房屋圖，此時，β(G)=β(TL1)=3=1+2；

假設當n=k時，結論成立，即有β(TLk)=k+2,下面證明n=k+1的情況.

由頂部梯狀圖的構造易知，TLk+1是在TLk基礎上增加了2個新頂點和3條新邊.顯然，只要在TLk的覆蓋里添加1個新頂點即可得TLk+1的一個覆蓋.則有β(TLk+1)=β(TLk)+1.從而β(TLk+1)=k+3=(k+1)+2.

因此，對于所有的n≥0，都有β(G)=B(TLn)=n+2.

定理3.2 若G是一個頂部梯狀圖TLn，則對于所有的n≥0，都有β′(G)=β(G).

證明 設G(V,E)是一個頂部梯狀圖TLn.

4 廣義梯形圖

設TLn1和TLn2是兩個頂部梯狀圖(兩邊的梯級數即梯形圖的尺寸分別為n1和n2)，連接TLn1和TLn2的兩個頂端點構成邊(稱之為橋)，產生的新圖記為L(n1,n2). 此類圖含有完美匹配，即為凱庫勒圖.

以L(n1,n2)的橋的兩個頂端點為基對再構造n3個梯級，記為L(n1,n2,n3).易知，這一類圖含有完善匹配.分別連接L(n1,n2)中的TLn1和TLn2兩組基對點構成邊(稱之為懸掛邊)，這樣產生的新圖記為L(n1,n2,M).

不失一般性，在頂部梯狀圖的頂端和基部分別構造橋和懸掛邊，產生的圖(圖4)記為L(n1,n2,n3，M)，稱為廣義梯形圖.

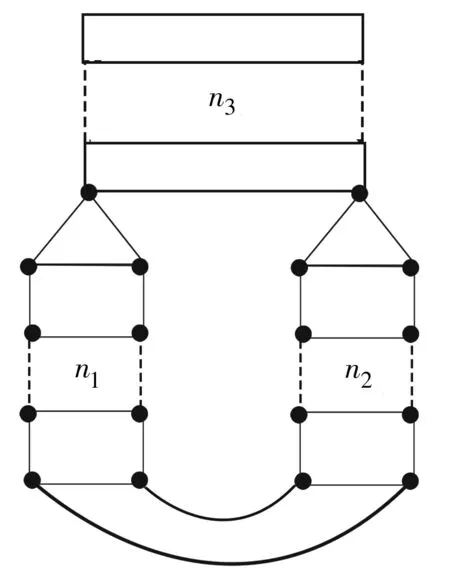
圖4 L(n1,n2,n3,M)

定理4.1 設G=L(n1,n2,n3,M)，則對于任意的n1≥0，n2≥0和n3≥0，都有β(G)=n1+n2+n3+4.

證明 分情況討論，

(1)若n1=n2=n3=0(圖5)，圖G中含有2個三角形、2個懸掛邊和1個橋，則需要從每個三角形中各選擇2個頂點來覆蓋圖中的9條邊.此時，β(G)=2+2=4.

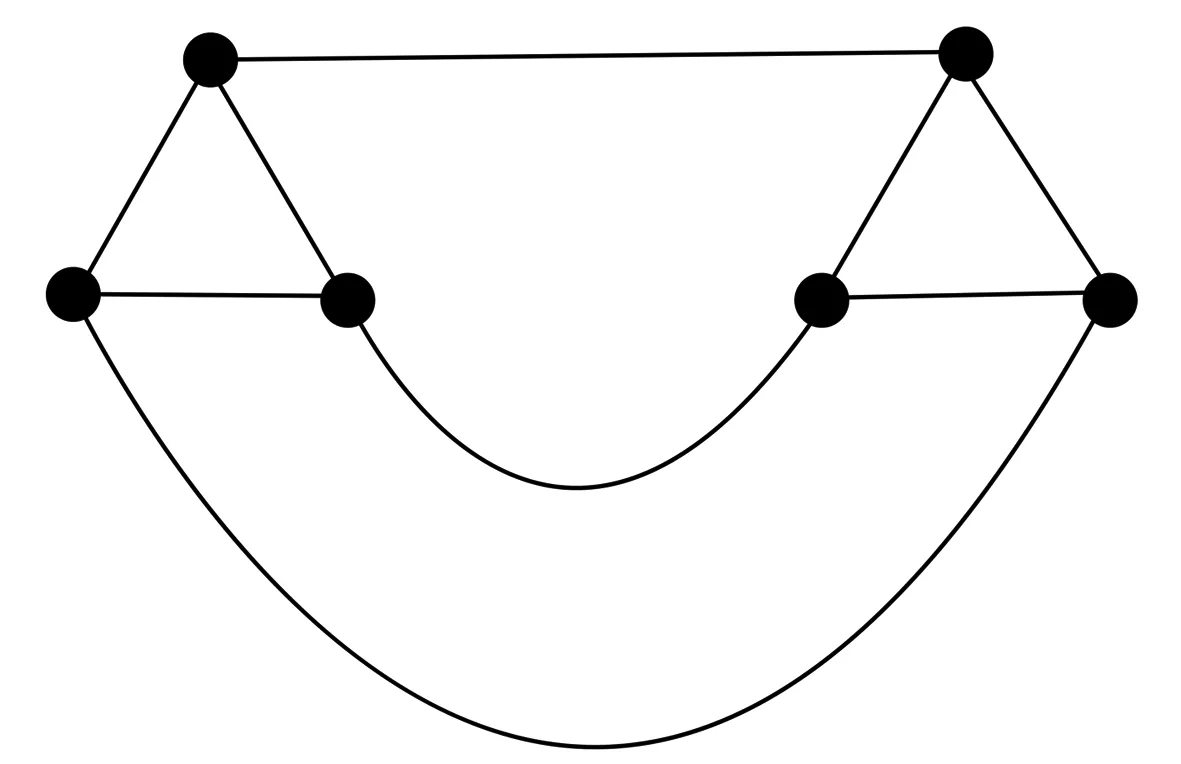
圖5 L(0,0,0,M)

(2)若n1=n2=0，n3≠0(圖6)，則需要n3個頂點覆蓋尺寸為n3的梯形圖，需要4個頂點覆蓋2個三角形、2個懸掛邊和1個橋.此時，β(G)=n3+4.

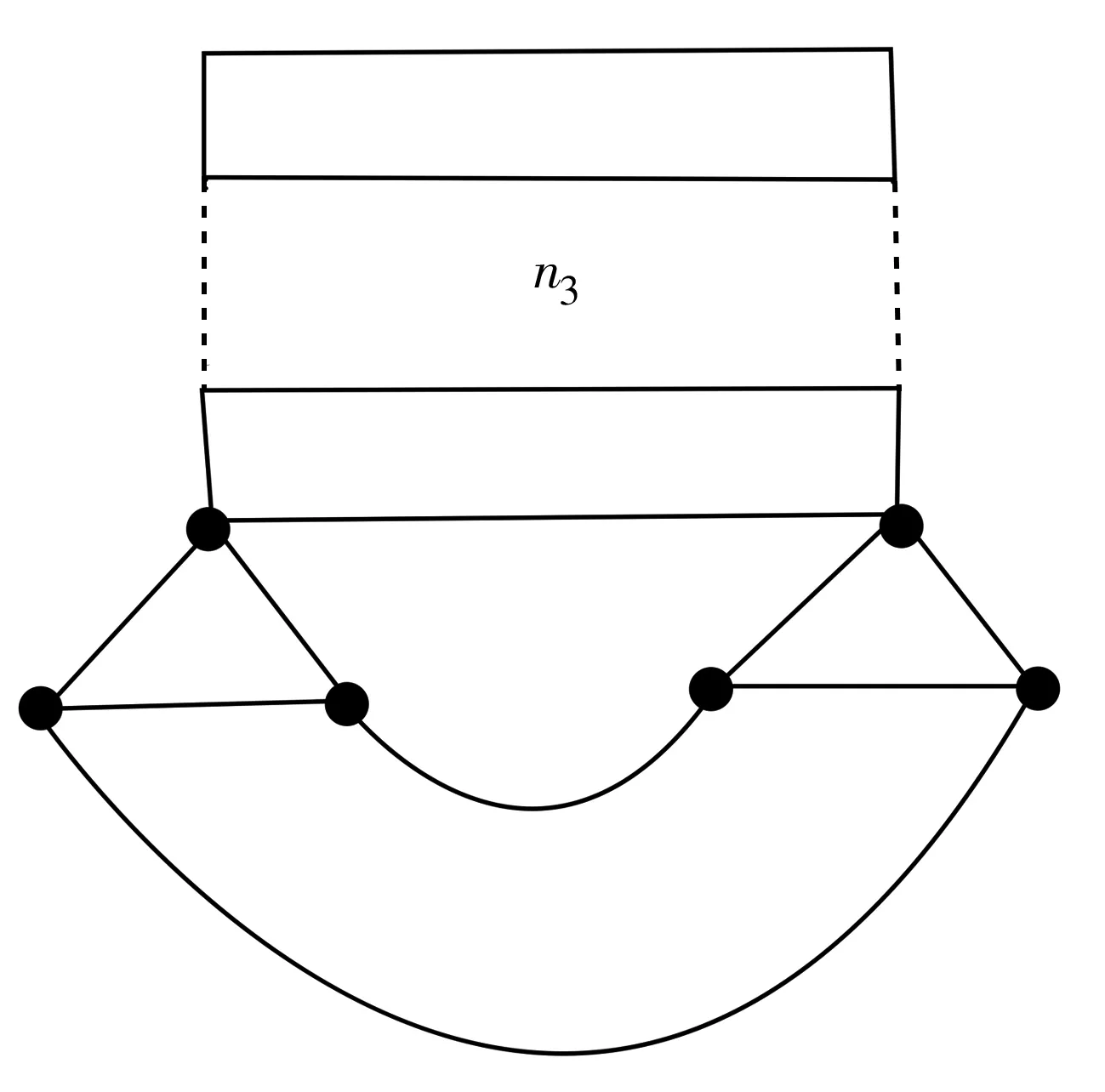
圖6 L(0,0,n3,M)

(3)若n1=n2≠0，n3≠0，則分別需要n1，n2和n3個頂點覆蓋圖G中3個梯級.同時，圖G中含有2個三角形、2個懸掛邊和1個橋，需要4個頂點來覆蓋.此時，β(G)=n1+n2+n3+4.

(4)若n1≠n2≠0，n3≠0，當n1n2時，所得圖是同構的.可得，β(G)=n1+n2+n3+n3+4.

定理4.2 設G=L(n1,n2,n3,M)，則對于任意的n1≥0，n2≥0和n3≥0，都有β′(G)=n1+n2+n3+3.

因為G=L(n1,n2,n3,M)含有完美匹配，所以，