基于分數階自抗擾的智能汽車超車軌跡控制
吳貞犇,楊 潘,王力超,劉丙友
(1.安徽工程大學電氣工程學院,安徽 蕪湖 241000;2.安徽達爾智能控制系統股份有限公司,安徽 蕪湖 241000)
0 引言
隨著交通運輸業的迅猛發展,交通事故頻發。由于超車過程復雜,因超車而引發交通事故是最多的狀況。為了減少交通事故,目前國內外利用智能控制技術對超車過程進行輔助控制[1-4]。
在車輛自動超車過程中,首先是利用云端技術檢測出車輛行駛的環境,然后通過計算到前車的行駛距離,進而規劃出一條安全的行駛軌跡,同時計算出所需的偏轉角度。針對路徑規劃主要有JEON等[5]提出的串釘算法、KRISHNAN等[6]提出的最優控制理論、LACAZE等[7]提出的基于搜索算法等。以上算法雖然能計算出超車的曲線,但是對于響應速度和抗干擾能力比較弱。
針對以上的問題,考慮自抗擾技術具有抗干擾、提高響應速度等能力,本文設計分數階自抗擾對整個超車系統進行控制。針對傳統的自抗擾技術對于信號的控制不能滿足真實的情況,通過對分數階理論的應用,設計基于分數階自抗擾控制的控制系統[8]。傳統自抗擾技術具有自解偶能力和不受系統模型的干擾效果,又具備更好的適應現實狀況的能力,更加適應對于智能車輛的控制[9-10]。并且加強控制系統的魯棒性,能夠增強汽車反應能力,使汽車的報警速度和剎車反應性能很大程度提升。對于自抗擾參數問題,本文利用模糊控制進行參數整定,減少了系統參數整定問題。同時給出系統的仿真結果,驗證了分數自抗擾技術控制車輛的優越性。
1 智能車輛超車系統
1.1 路徑規劃
直線超車前兩車相對運動車速一定,整個過程智能車輛之間的車速趨于不變,且在車道的中心線上行駛,由此建立超車路徑規劃,如圖1所示。
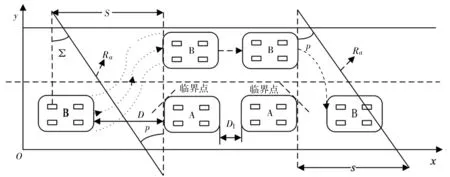
圖1 汽車超車路徑軌跡圖
由圖1可知,在a秒后前車A位移D1m,其中,Ra表示當B車超過A車時,兩者的運行轉角中心距離。考慮碰撞問題,即
(1)
其中,D代表安全距離。
所有轉彎半徑如下:
(2)
(3)
其中,L3為車寬,L4為車長,L5為平行前進時左輪輪距,D為未超車時車距,D1為超車過程前車行駛距離。駕駛車輛轉彎的半徑范圍為(Rmin,Rmax)。
1.2 運動學模型
在車輛運動中要考慮汽車的運動學模型,通過準確的運動學模型能夠真實地反映汽車的運動狀況。在汽車準備超車時,汽車后車輪與地面之間滿足滾動約束條件,在超車過程中兩輛車為相對運動。圖2為汽車模型的受力分析圖。
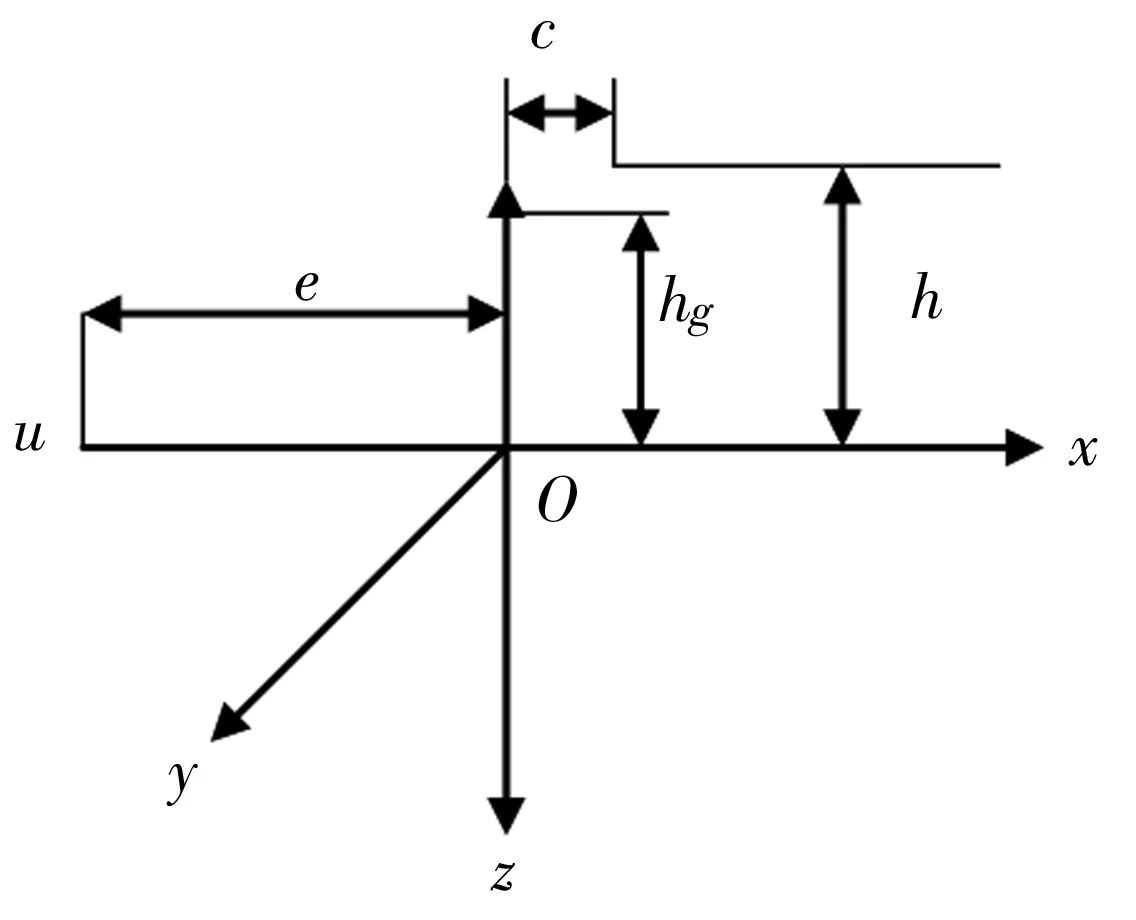
圖2 汽車模型受力圖
在圖2中,汽車的三自由度分別代表x軸、y軸和z軸方向轉動的自由度,一般用橫向速度v、橫擺角速度r、側傾角φ來表示。
汽車三自由度模型的微分方程為
(4)
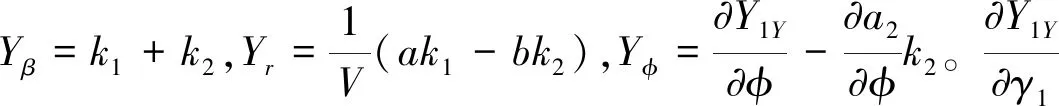
Yδ=-k1
(5)
(6)
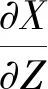
(7)
(8)
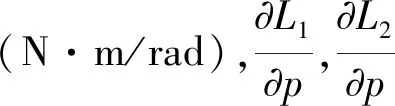
Np數值比較小,可以忽略不計,由v=pV可知:
(9)
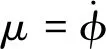
(10)
將此方程組表達成矩陣形式,即:
(11)
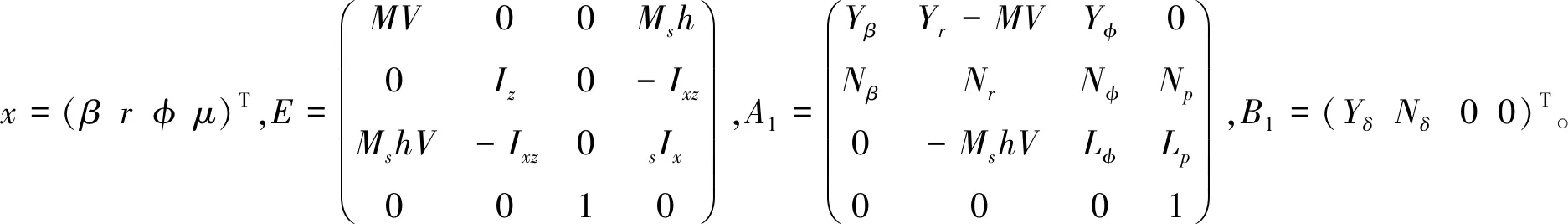
標準形式如下:
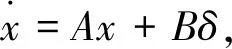
(12)
其中,A=E-1A,B=E-1B。
利用自抗擾技術自解偶功能,對各個自由度進行控制,協調工作。自抗擾解耦控制框架圖如圖3所示。利用自抗擾自解偶過程,可以解耦控制前后和側向移動信息,達到同時工作且互不干擾。
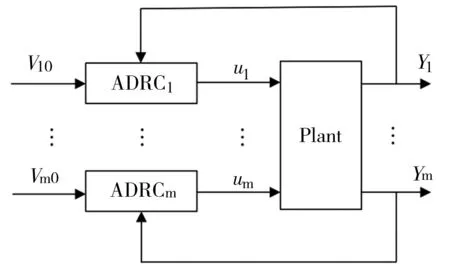
圖3 自抗擾解耦控制框架圖
2 分數階自抗擾控制器
控制系統動態響應是研究系統的重要標準,當系統受到干擾時,為了確保系統能保持理想狀態,本文利用自抗擾技術來控制智能車的超車行駛軌跡,消除行駛時受到的外界干擾和建模不確定部分帶來的影響,確保行駛軌跡的理想化。
2.1 跟蹤微分器結構
控制系統中存在動態響應,為了減少系統外部所受干擾,系統響應能夠快速恢復到穩定狀態,而引入跟蹤微分器(TD),解決噪音帶來的影響,并得到所需要的提取連續信號和微分信號。提供過渡階段,實現平滑穩定的變化。
(13)
其中,fhan代表fhan函數,x(t)為理想的軌跡輸入信號,v1為對理想軌跡的跟蹤信號,v2為v1跟蹤信號的微分,r0為跟蹤速度因子,h0為濾波因子,h為積分步長。
(14)
跟蹤微分器的參數主要取決于r0和h0,當輸入為常值1的階躍信號,且r0=10,h0=0.02時,輸出如圖4所示。
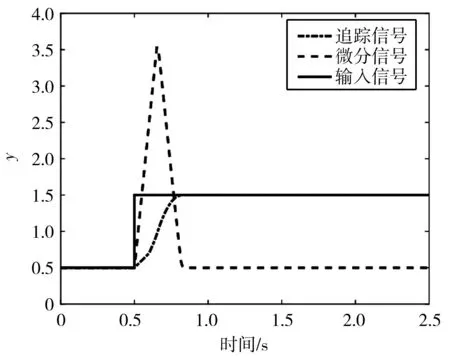
圖4 跟蹤微分器響應曲線
2.2 改進型狀態觀測器(PESO)
現實狀況基本是分數階系統,在傳統的自抗擾技術的基礎上利用分數階原理進行改進,使整個觀測器運行效果更好。具體算法如下:
(15)
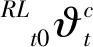
(16)
為了驗證fnew(·)的優越性,選取σ=0.01和a=0.25,分別與兩種傳統的非線性函數fan函數和fal函數對比,如圖5所示。
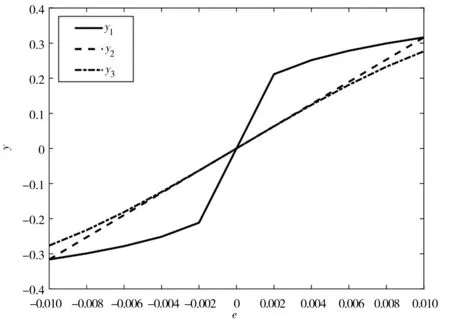
圖5 非線性函數響應曲線
在圖5中,y1為fan函數響應曲線,y2為fal函數響應曲線,y3為本文提出的新型fal函數響應曲線。由圖5可以看出,改進型非線性函數具有更好的平滑性和連續性,對狀態觀測器的控制起到高頻抑制作用,增強了觀測器的觀測效果。
2.3 非線性狀態誤差狀態反饋控制律
非線性狀態誤差狀態反饋控制律(NLSEF)具有消除擾動作用,對于TD傳輸的信號和反饋的信號進行處理,得到擾動補償的響應結果,數學表達式如下:
(17)
針對NLSEF雙輸入單輸出的效果,取不同a會導致輸出的形狀發生變化,而調節σ主要是對非線性函數產生影響,因此可適當調節σ來防止函數的初始位置晃動。
2.4 系統整體框架
根據上述設計方案,建立控制器的系統結構圖,如圖6所示。
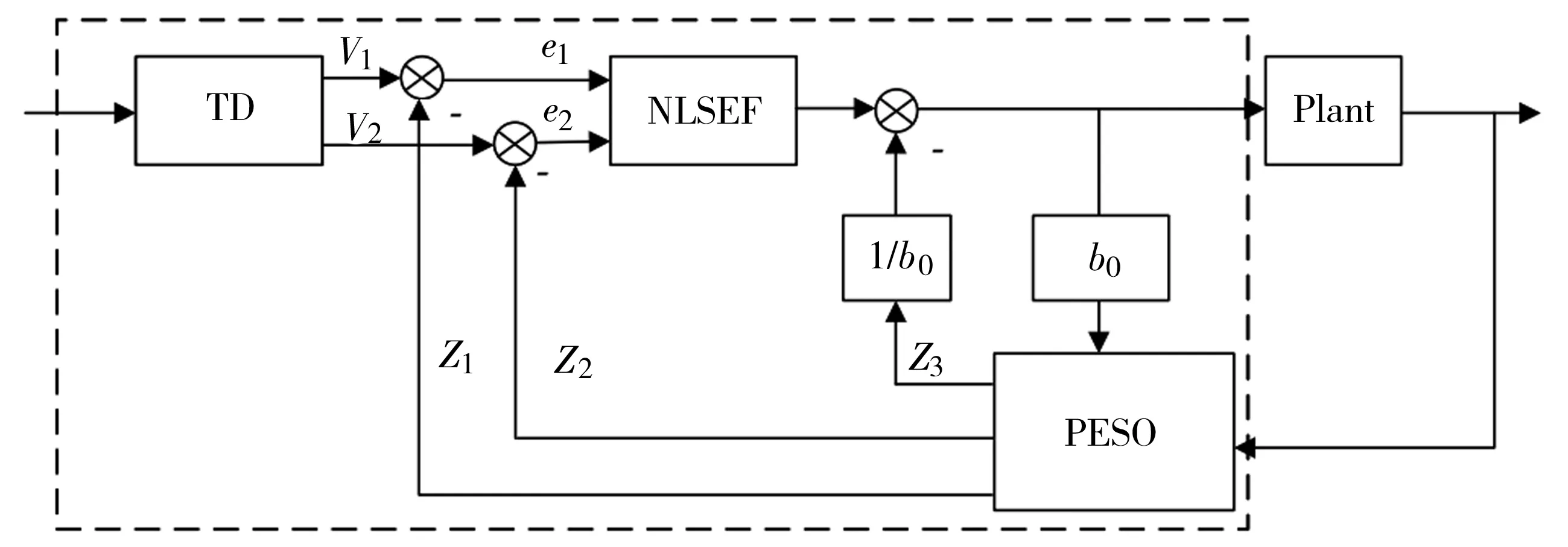
圖6 系統框架圖
研究對象為汽車的運動學模型,而完整的自抗擾控制器包含跟蹤微分器、誤差反饋控制率和狀態觀測器三大模塊,能夠很好地抑制內外部干擾引起的波動。
3 仿真實驗
仿真汽車的系統參數如表1所示。根據表1數據,利用改進的自抗擾器進行仿真,仿真結果如圖7所示。數據對比如表2所示。
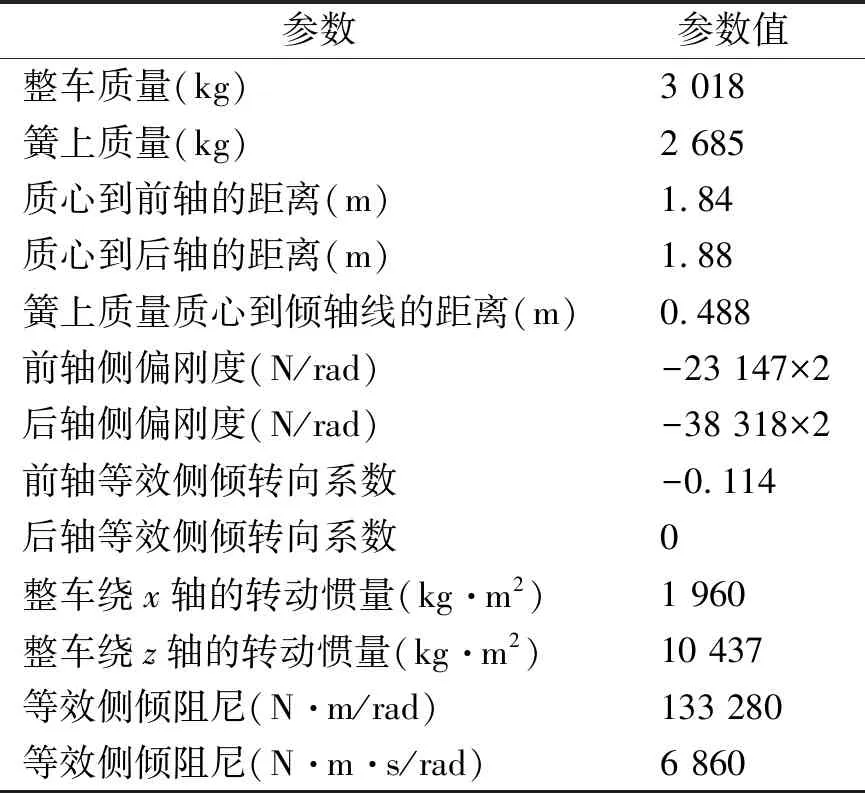
表1 系統參數
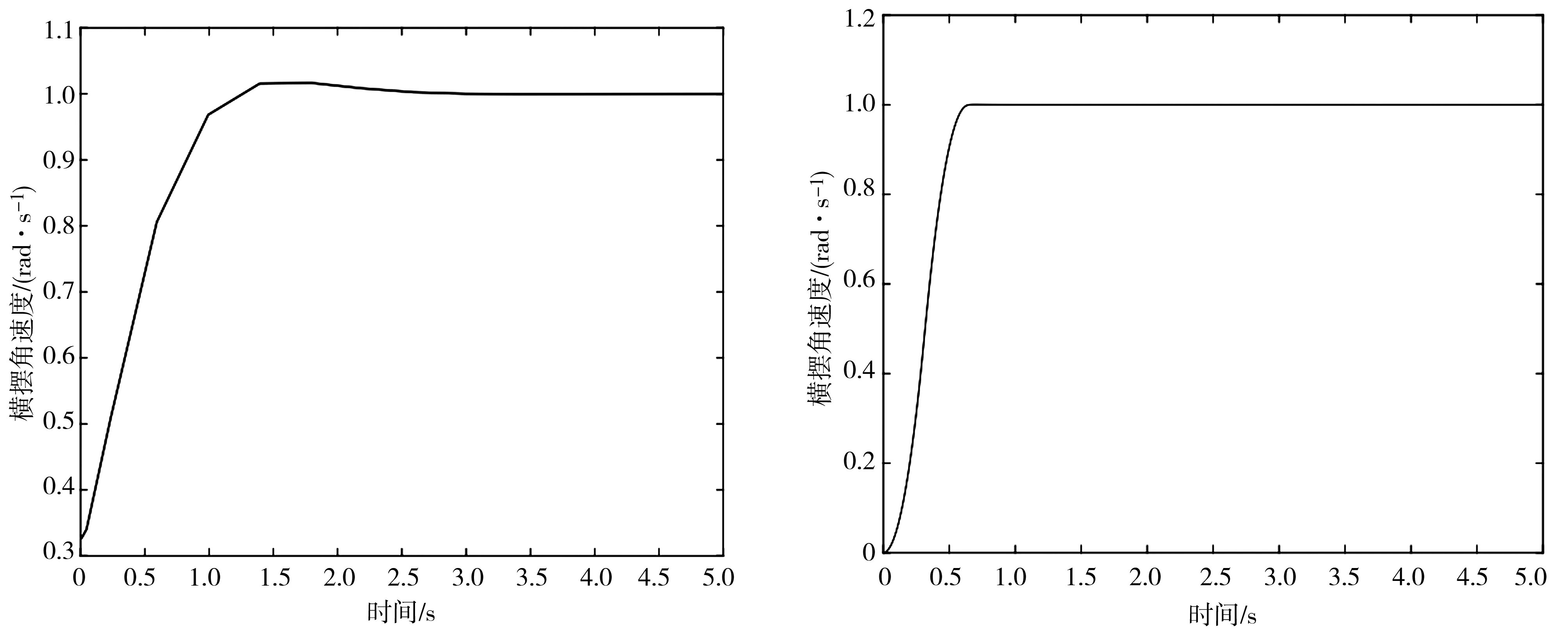
(a)傳統自抗擾技術橫擺角速度與時間關系曲線 (b)分數階自抗擾技術橫擺角速度與時間關系曲線
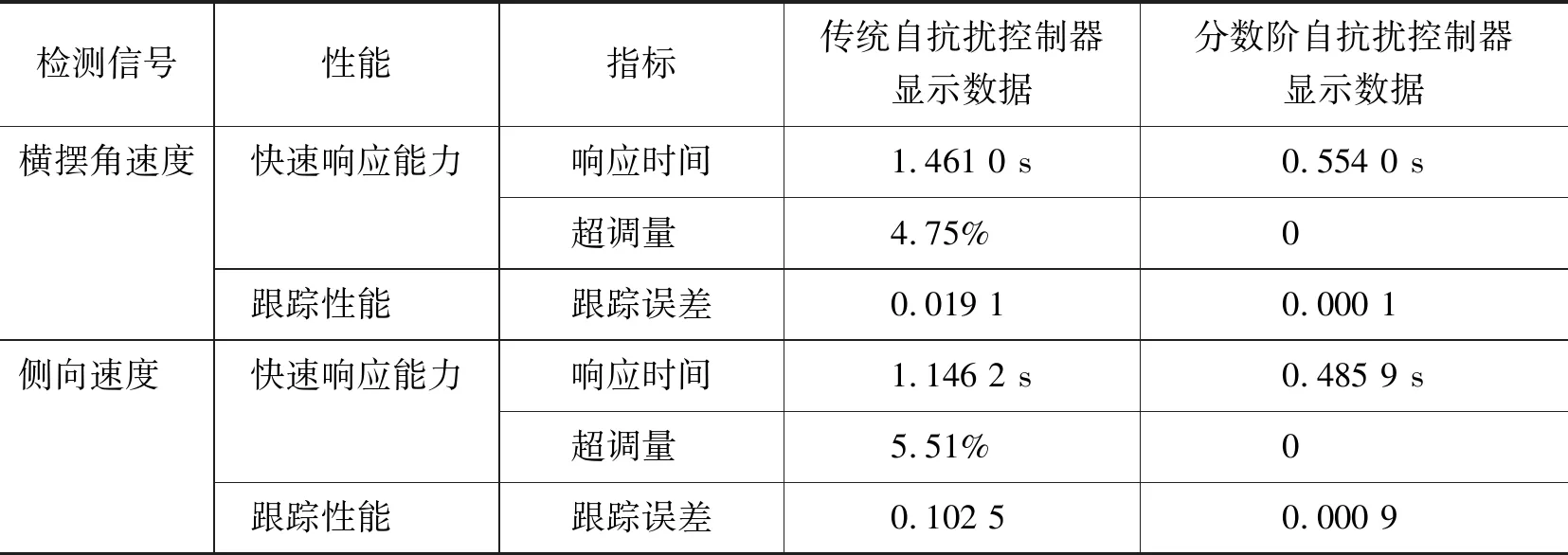
表2 兩種控制策略性能比較
通過仿真結果和表2可知,當橫向速度恒定為13 m/s時,輸入前輪轉角角速度為1 rad/s時,利用傳統自抗擾技術控制車輛得到的結果如圖7(a)(c)所示。圖7(b)(d)是利用分數階自抗擾控制技術控制車輛的響應系統的的響應曲線圖,對比可知改進型控制裝置響應速度更快,超調量更少。
4 結語
本文設計了基于分數階自抗擾技術控制的智能汽車的超車系統,采用分數階控制,提高了汽車超車整個過程中的穩定性、快速性和抗干擾能力,降低了汽車行駛外界干擾和汽車自身的控制復雜性對超車的影響。該系統可實現對智能汽車超車過程中側向速度和橫擺角速度的優化,實現對汽車的高精度、高速度和強穩定控制,滿足目前智能汽車超車過程的控制要求。

