類比法在RLC串聯電路分析中的應用

張宏根

（浙江省杭州學軍中學，浙江杭州 310000）

物理學中不少不同部分的知識點之間有著緊密的聯系，挖掘它們之間的關系，有助于理清物理學的知識脈絡，并能夠使所學的知識融會貫通.物理學習的研究方法很多，其中類比法是較為常見的一種研究方法.類比法指的是由一類事物所具有的屬性，推測出其它類似事物也具有這種屬性的一種推理方法.［1］這種方法能把具有相似之處的物理知識點放在一起進行對比，從而起到幫助記憶、加深理解，提高分析問題和解決問題的能力.［2］通過近年來的中學物理教學工作，筆者深刻認識到在教學中傳授知識固然重要，但掌握好的學習和研究方法則可以讓我們的學生終生受益.因此，在物理教學中教師應該注重傳授物理學的研究方法，使學生學會運用這些方法解決問題，尤其是針對學習物理競賽的學生，顯得尤為重要.以下筆者就以RLC電路為例，探索類比法在物理學習和解題中的應用.

1 RLC串聯電路的類比研究

物理中的不同知識點之間可能存在關聯性和相似點，比如RC電路與RL電路，RLC 串聯電路和LC電路分別與阻尼振動和簡諧運動之間都具有很大的相似性，因此可以通過類比，將一種研究方法應用到另一種上，從而快速得出結論.以下就舉例作簡單的說明.

1.1 RC和RL串聯暫態電路的類比

圖1 顯示的是RC 串聯電路，其中電源電動勢為E，電容為C，電阻為R.電容器充電后將電鍵開關接到2 的位置，電容器C通過電阻R放電，在放電的暫態過程中，電流i隨時間t的變化關系可以通過基爾霍夫第二定律得到，具體如下.［3］

圖1 RC串聯電路示意圖

通過對（1）式求導，并結合（2）式，得到RC 電路在放電暫態過程中的電流，即

可見，電路中的電流以指數形式變化，定義RC 串聯電路的時間常數τ＝RC.

圖2顯示的是RL串聯電路，其中電源電動勢為E，電感為L，電阻為R.對比圖1和圖2，不難發現二者有很大的相似性，因此，可以類比RC 電路來分析RL 電路.當電鍵開關從1快速撥向2時，設初始條件t＝0時，i0＝.可以通過基爾霍夫第二定律，類比RC串聯電路的（1）式，可以得到［3］

圖2 RL 串聯電路示意圖

將（5）式和（3）式對比，不難發現二者高度相似，所以可以類比得出（5）式的解

通過以上對比分析不難得出短接的RC和RL電路暫態放電過程具有很大的相似性，表1 是二者的對照關系.

表1 短接的RC和RL電路暫態過程對比

1.2 RLC串聯電路和阻尼振動的類比

圖3 顯示的是RLC 串聯電路，其中電源電動勢為E，電容為C，電阻為R，電感為L.假設電鍵開關從1快速導通到2，則在放電的暫態過程中，電流i隨時間t的變化關系可以通過類比上述RC和LC 電路方法，由基爾霍夫方程得到，具體如下.［3］

圖3 RLC串聯電路示意圖

將（2）式代入可得

此式與阻尼振動，即物體以不太大的速率在黏性介質中運動時，其阻力與運動的速率成正比（f＝－γv）情況下的微分方程類似，可以對兩者進行類比.其中阻尼振動方程如下.［4］

綜上所述，RLC、LC 串聯電路分別與阻尼振動、簡諧運動類似，其對應的電路物理量和振動的動力學物理量之間的對應關系如表2所示.

表2 RLC電路和振動的動力學各物理量的對應關系

2 類比法的應用舉例

通過前述的類比我們發現：RLC 電路和動力學振動之間有極大的相似性，這種相似性表現在其方程的同構上.所以很有必要探索利用RLC 電路的相關知識來求解與之相似的動力學振動問題，或者利用動力學振動知識來求解RLC 電路問題，以期獲得更為簡潔的求解方法.以下就以兩個相關的高中物理題舉例說明.

例1.如圖4，豎直勻強磁場B中放有兩條平行無限長導軌，間距為l，導軌光滑無摩擦且為理想導體.在導軌上平行放著兩根完全相同的質量為m的導體棒，每根棒上串聯有電阻R，電容C，導體棒與導軌接觸良好.初始時，棒1具有指向棒2 方向的速度v0，電容上無電荷，兩棒間距足夠大不會相撞.

圖4

（1）求出電流隨時間變化關系.

（2）將題中的電阻改成L的電感，其余不變，求電流隨時間變化關系.

解析：此題的導體棒以一個初速度運動，可以類比為已經充電的電容器，其電壓可以用導線切割磁感線產生的電動勢Blv0來表示.在隨后的運動過程，可以類比為RC的放電暫態過程和LC 電路的自由振蕩過程.具體求解方法如下.

（1）如圖5，假設兩導體棒的運動速度分別為v1和v2，電流流向如圖5 所示.由牛頓第二定律可得

圖5

根據基爾霍夫第二定律，可得

兩邊求導，并結合（11）、（12）和（2）式，可得

令

則總電容就為C′，（14）式可以寫成

（2）當電阻改為電感L時，根據基爾霍夫第二定律，并類比（13）式可得

兩邊求導，并結合（11）、（12）和（2）式，可得

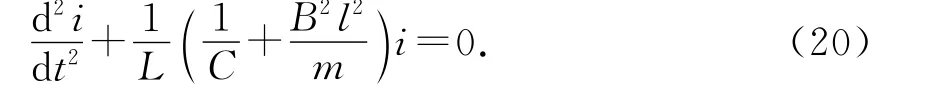
將（15）式代入可得

將（21）式和簡化的（8）式相比較，可以看出：兩式具有完全一致的形式，所以串聯電感的導體棒的運動過程可以類比為LC振蕩電路.對照（10）式的解的形式，將串聯電感電路中的C′、E0（＝Blv0）分別和LC 振蕩電路中的C、E作類比，不難得出（21）式的解

例2.如圖6所示，一個磁感應強度為B的均勻磁場，垂直于一軌距為l的導軌平面，軌道平面與水平面有α的傾角.一根無摩擦的導體棒，質量為m，橫跨在兩根金屬導軌上.若開關依次接通1、2，使電容為C或電感為L的元件與棒構成電路，當從靜止放開導體棒后，求棒的穩定運動狀態.

圖6

解析：此題是將電容或電感與導體棒切割磁感線運動組合的一類問題.當開關接1，導體棒與電容器構成回路，導體棒開始以加速度a運動，并產生動生電動勢而對電容器充電，同時電路中產生電流，此時棒會受到一個反向的安培力作用.當開關接通2，導體棒與電感線圈構成回路，棒開始運動后，隨著速度增大，產生的動生電動勢增大；電動勢直接加在線圈兩端，因此通過線圈的電流增大；而導體棒受到安培力的作用，越過平衡位置后減速，直至速度為0.電路電流開始時逐漸增大，在導體棒達到最低點時電路中電流最大.隨后導體棒因安培力作用往回加速，動生電動勢使電流減小，直至導體棒回到初始位置，電流減小為0.再重復上述過程，形成簡諧運動.求解這類問題的常規方法是將導體棒和電容、電感分開分析，對導體棒應用動力學知識列方程；對電容、電感利用電學知識列方程.求解過程較為繁雜.我們可以根據例1的結論來進行求解，可以極大的簡化求解過程，具體如下.

此時，就不需要考慮電學方面的問題，直接根據動力學知識，即牛頓第二定律就可以列出方程

此時的串聯電路可以等效為LC振蕩電路，得到其電流方程

從題中不難看出導體棒也將在平衡位置附近作簡諧運動，此題通過類比法，將簡諧運動化為LC 自由振蕩電路求解，將極大簡化計算過程.

不難得出當電流最大時，為導體棒的平衡位置，此時導體棒受力平衡，即重力沿著軌道的分力mgsinα和安培力ilB是一對平衡力，即平衡位置處的電流i0為

由題意知，初始時刻t＝0時的初始電流i＝0，可以類比LC振蕩電路的解，并結合（27）式，得出（26）的解

在導體棒與電感線圈構成回路中，電壓與電流的關系為

對（29）式兩邊積分，由初始條件，x＝0時i＝0，可得

將（28）式代入（30）式中，可得

即導體棒在作簡諧運動.

3 結論

通過對RC和RL 電路類比，得出二者物理量之間的相似點；通過對比RLC 電路和阻尼振動，以及LC振蕩電路和簡諧運動，得出電學量與力學量之間的對應關系.這種類比法不僅便于學生快速掌握相關知識點，也有利于在解題和學習中開拓思維，觸類旁通.為此，通過舉例，利用導體棒做切割磁感線運動時的可以等效為電容C，進而可以通過RC 和LC 電路知識來求解這類電路串聯電容和電感的相關問題；或者利用B2l2C將電容等效為質量m*，利用力學方法來求解電學問題.通過例題展示不難可以發現，使用這些方法可以得到更為簡潔的求解過程.