數(shù)學課堂中基于深度學習的核心問題設計

李 衡

（福建省福清市瑞亭小學）

數(shù)學核心素養(yǎng)的形成離不開特定的數(shù)學活動。傳統(tǒng)的師生一問一答、死記硬背、題海戰(zhàn)術的學習方式，無法實現(xiàn)學生學習的主動參與、思維的深度發(fā)展，更談不上數(shù)學核心素養(yǎng)的形成。在具體問題情境中的深度學習，強調(diào)學生問題的生成、知識結構的整合、深度的理解、思想方法的遷移和應用，以此逐步形成核心素養(yǎng)所強調(diào)的必備品格和關鍵能力。課堂教學中，核心問題對驅(qū)動深度學習有著重要意義。圍繞著深度學習的展開，教師把握核心問題的內(nèi)涵意義、結構特征、實踐策略，讓學生的深度學習真正發(fā)生，是培養(yǎng)學生數(shù)學核心素養(yǎng)的重要途徑。為此，教師要通過設計核心問題，引領學生達成深度學習。

一、把握核心問題的內(nèi)涵意義，讓深度學習具有動力

深度學習指的是基于理解的學習。深度學習關注學生參與學習的動機，關注學生在活動過程中的理解建構，關注學生在思考過程中的遷移和應用。深度學習離不開學習情感的積極支持與思維的劇烈碰撞，而問題是數(shù)學思考的“引擎”，因此學生的深度學習特別需要核心問題的引領與驅(qū)動。上海市特級教師潘小明對核心問題的定義是：基于課時核心知識和學生的認知水平，關注數(shù)學核心素養(yǎng)，引領課堂教學情境性的問題。教師明晰核心問題的內(nèi)涵和意義，有利于改進教學設計，增強學生深度學習的主動性。

（一）核心問題可激發(fā)學生參與學習的積極性

新課程背景下，數(shù)學課堂教學應以問題為開始，以解決核心問題為主要任務。核心問題的產(chǎn)生應源自學生提出的問題，然后師生一起把這些問題梳理并進一步凝練、升華，形成核心問題。因為問題源自學生，他們在數(shù)學學習時就不會再“被牽著鼻子走”，學生解決問題的主動性就會增強。由于問題是學生提出的，比較接近學生的“最近發(fā)展區(qū)”，因此學生對問題的理解與探索相對容易，只要“跳一跳”就可以解決問題。這樣，學習過程既有挑戰(zhàn)性，學生又能較為輕易地克服遇到的困難，從而激發(fā)了學生解決問題的積極性。

（二）核心問題可發(fā)展學生的數(shù)學思維

深度學習的本質(zhì)是實現(xiàn)深度思維。核心問題統(tǒng)領若干個相關聯(lián)的小問題形成“問題串”，學生在學習過程中圍繞“問題串”展開探究活動，這樣“問題串”就轉化成了“活動串”。在體驗活動的過程中，學生的學習活動在“問題串”的引導下層層深入，又構成了一條思維深度發(fā)展的“思維串”。深度學習就是借助“問題串”展開體驗活動并發(fā)展學生的深度思維。

（三）核心問題可提升學生的數(shù)學素養(yǎng)

學生進行數(shù)學學習不應僅僅是學到知識，更多的應是通過學習活動提升學習能力和端正學習態(tài)度。核心問題統(tǒng)領下的課堂教學是以學生小組合作學習方式進行的，在這個過程中，需要學生思考、傾聽、表達等學習能力的參與，同時通過同學之間的互動，學生的情感、態(tài)度和價值觀也得到了提升。

二、遵循核心問題的設計原則，讓深度學習有路徑可尋

核心問題是引領數(shù)學課堂深度學習的原動力和牽引力，核心問題與相關聯(lián)的小問題構成了“問題串”，遵循特定原則，把學術形態(tài)的教學內(nèi)容轉變成教育形態(tài)的問題研究。核心問題引發(fā)深度學習要突出以下四個原則。

（一）可及性和挑戰(zhàn)性原則

核心問題的深度、難度、廣度要與學生的知識和能力水平相適應。核心問題的提出要符合學生的學習規(guī)律和當下的認知水平，教師應找到學生的“最近發(fā)展區(qū)”，以此來設置核心問題。這樣，學生既能夠在力所能及的范圍內(nèi)探究和解決問題，又能夠避免因為問題過偏、過難而喪失對數(shù)學學習的興趣。此外，核心問題的設計也不能一成不變，對學生沒有任何挑戰(zhàn)。教師要根據(jù)學情，設計能讓學生“跳一跳夠得著”的核心問題，引領學生走向深度學習，發(fā)展學生的數(shù)學思維。

（二）典型性和針對性原則

核心問題的設計應符合數(shù)學學科本身的知識特點和學習規(guī)律，具備典型的數(shù)學特征。問題設計不能盲目追求調(diào)動學生的學習興趣，不能脫離數(shù)學知識本身，也不能脫離學生的實際數(shù)學學習情境。此外，核心問題也要有針對性，應設計在重要數(shù)學概念及數(shù)學規(guī)律的理解、分析之處，要通過核心問題使學生形成處理問題的典型思路、方法，了解知識間的內(nèi)在聯(lián)系以及易錯、易混的問題等。教師要抓住學生理解和應用知識的關鍵處來提出核心問題，使教學擊中要害，培養(yǎng)和發(fā)展學生的分析能力和綜合能力。

（三）具體性和探究性原則

教師設計的核心問題應明確而具體，簡單而有效，其內(nèi)容不能過于寬泛，那樣會分散學生的精力，使學生抓不住問題的本質(zhì)，甚至會因為一些無效的問題環(huán)節(jié)使學生走向問題解決的反方向，浪費寶貴的教學時間，降低教學效率。此外，教師還要通過設計核心問題來引領學生去探究。在問題提出的過程中，教師可以設置懸念，揭示矛盾，從而激發(fā)學生主動探究的欲望，引導他們積極參與，在探究中獲取新知。

（四）程序性和啟發(fā)性原則

程序性指的是核心問題的解決過程要與學生數(shù)學思維發(fā)展的順序一致。教師設計的核心問題要有利于啟發(fā)學生的邏輯思維，使學生把握住核心問題的實質(zhì)。程序過于精細，核心問題的環(huán)節(jié)過于顯露，引不起爭論，不利于學生思維的展開；程序粗放，隱含條件太多、太隱蔽，學生不容易抓住要領，也會使關于核心問題的對話交流無法深入開展。此外，核心問題的設計還要有啟發(fā)性，要啟發(fā)學生通過理解和解決問題，逐漸深度思考，形成自己的數(shù)學思維。

三、形成核心問題的實踐策略，讓深度學習真實發(fā)生

課堂教學要以核心問題的提出作為教學的起點，以在教學過程中解決問題作為主要任務。教師要組織學生根據(jù)問題開展自主學習、動手操作、小組討論、集體交流、問題再生成等學習活動，完成解決問題的過程。

（一）圍繞教材內(nèi)容設計核心問題

核心問題指向的應該是數(shù)學知識的核心內(nèi)容，所以，教師要深入分析教材，理解教材的核心內(nèi)容，把握知識的本質(zhì)，從而設計出高質(zhì)量的核心問題。

1.圍繞概念關鍵詞設計核心問題

數(shù)學概念具有高度的概括性，概念中的關鍵詞更是濃縮的精華，教師理解好關鍵詞，就能提綱挈領地幫助學生理解概念。如教學“周長的認識”時，周長的概念為“封閉圖形一周的長度，是它的周長。”學生對于關鍵詞“一周”的理解，認為就是“一圈”的意思，這是用生活語言來解釋。但是，教師如果僅止步于此，學生的理解就不夠深刻，教師應該更進一步，設計核心問題：“一周”是什么意思？你能結合圖形邊比劃邊說嗎？從而讓學生明晰“一周是從起點回到起點，一周與方向、起點無關”。理解了這個意義，學生也就能明白，周長之所以是封閉圖形，是因為只有封閉圖形才能從起點又回到起點。所以，本節(jié)課應圍繞核心問題“一周是什么意思”展開教學活動。

2.圍繞概念的形成設計核心問題

有的概念看似很簡單，學生很容易學明白，但越是簡單就越容易出現(xiàn)理解偏差。學習概念時，學生只有深入地感知其形成過程，逐步建構其形成表象，才能在未來的學習中使其得到正確地拓展和提升。如教學“長方體和正方體的認識”一課，如何讓學生理解長、寬、高對于長方體的重要性呢？在教學中，教師可把“長、寬、高有什么意義”作為核心問題展開教學活動，通過一“搭”一“拆”，讓學生經(jīng)歷“長、寬、高決定長方體的大小”這一核心概念的形成過程。學生先選擇12根小棒搭一個長方體的框架，教師相機提問題：“如果拆掉其中的一條棱，你能比劃出它的大小嗎？”“還能再拆掉一些棱嗎？至少要剩下幾條棱才能還原這個長方體的大小呢？”教師放手讓學生自主探索實驗、討論交流，學生得出結論：至少要剩下相交于一個頂點的三條棱。學生認為，因為長方體相對的四條棱長度相等，共有三組，通過余下這一組的三條棱就可以還原每組其余的三條棱。教師并沒有停下而是繼續(xù)去掉高，只剩下長和寬，學生發(fā)現(xiàn)，此時只能確定一個面，無法知道這個長方體有多高。教師再去掉長、寬，學生得出，只知道長方體的高，無法確定長方體的面。最后，教師提出核心問題：長、寬、高的意義是什么？從這個探索活動中，學生悟出：長、寬、高決定一個長方體的大小，它們對于長方體有著至關重要的意義。

3.圍繞概念的關聯(lián)設計核心問題

數(shù)學知識之間有其內(nèi)在的聯(lián)系，知識點分散到每節(jié)課的問題中時雖然不一樣，但是其本質(zhì)相同，因此其核心問題往往是一樣的。由于這些問題之間屬于平行關系，所以我們應該整合相關聯(lián)的內(nèi)容，提煉出核心問題，使學生達到對知識的整體理解。如“商中間、末尾有零的除法”一課中有3個例題：309÷3=103、420÷3=140、832÷4=208。很多教師往往分散進行教學，先讓學生感受被除數(shù)有零、商有零，再感受被除數(shù)沒有零、商有零的情況。這3個例題有其不同點，但本質(zhì)是一樣的，都是因為“被除數(shù)某位除以除數(shù)不夠商1”。所以，寫零與被除數(shù)是否有零沒有直接的關系。因此，教師可提煉出其核心問題：商中為什么寫零？教師可以把這3個例題整合在一節(jié)課中進行教學，讓學生感受“零的產(chǎn)生并不是因為被除數(shù)中有零”的原因，從而讓學生對算理的理解更加深刻、到位。

（二）根據(jù)學情設計核心問題

教師設計的問題要接近學生的“最近發(fā)展區(qū)”才有利于解決，所以，教師要關注學情，因為學生的錯誤點和困惑點就是解決問題的關鍵。以此來設計核心問題，往往能起到事半功倍的作用。

1.在錯誤資源中生成核心問題

沒有無緣無故的錯誤，學生的每一次錯誤都應引起教師的反思。尤其是出錯率較高的地方，往往正是學生最難理解之處，解決了這個錯誤，就能加深學生對新知的理解。如教學“乘法分配律”一課，學生在運用規(guī)律進行簡便計算時出錯率相當高，常犯的錯誤是相同因數(shù)只乘了一次，即（120+30）×6=120×6+30。教師反復強調(diào)，可是強調(diào)多了學生又與乘法結合律混淆，出現(xiàn)如（120×30）×6=120×6×30×6這樣的錯誤。為什么會產(chǎn)生這樣的錯誤呢？我發(fā)現(xiàn)，問題都指向?qū)W生對乘法分配律中算式兩邊“6”的意義沒有理解好，所以學生對規(guī)律的運用生搬硬套。當學生提出“為什么左邊的算式只有一個6，右邊的算式卻要寫兩個6呢”這個核心問題時，根據(jù)規(guī)律形成的特點，我擬定了“數(shù)、事、形、理”的“問題串”。“數(shù)”是根據(jù)例題引導學生發(fā)現(xiàn)（120+30）×6與120×6+30×6的區(qū)別，教師提出問題：“觀察這兩個算式有什么規(guī)律？”通過觀察，學生初步建立起乘法分配律的模型。“事”是把規(guī)律還原到生活中，教師提出問題：“生活中還能舉出這樣的例子嗎？”用生活的例子來解釋數(shù)學模型，能幫助學生深刻地理解抽象模型的內(nèi)涵。“形”是學生根據(jù)自己舉出的例子抽象出模型，教師提出問題：“這些例子能用算式來表示嗎？”通過大量的算式，學生加深了對乘法分配律算式模型建立的印象。“理”就是理解乘法分配律的算理，也就是學生提出的核心問題：“為什么左邊的算式只有1個6，右邊的算式卻要寫2個6呢？”經(jīng)過大量生活實例的鋪墊，學生很快就找到了答案：“這3個‘6’的意義不同，左邊算式表示6套衣服，分配到右邊變成是6件上衣加6條褲子，如果右邊少了1個6，那就只有6件上衣和1條褲子，只能湊成1套，湊不成6套衣服了。”看似復雜的概念，學生借助“6條、6件、6套”這3個數(shù)量輕輕松松就“搞定”，而且學生還進一步認識了乘法分配律的內(nèi)在含義。這樣，就比單純從算式意義上來理解或通過公式的記憶順暢多了，使看似復雜的問題變得簡單易懂了。

2.在學生困惑處生成核心問題

從一定意義上來說，教學的過程也是一個解惑的過程，學生的疑問之處正是教學中最值得探究的地方。教師要分析學生形成困惑的原因，追根溯源，找出核心問題。如在教學“長方體的體積”一課中，當學生得出長方體的體積=長×寬×高時，再通過底面積=長×寬，又可引導出長方體的體積=底面積×高。我們通常都認為這個推導合情合理，可是學生卻有疑問：“底面積×高為什么會得到體積呢？體積怎么會跟底面積有關系呢？”這些疑問提醒我們要找準核心問題的實質(zhì)：體積公式的意義，即長×寬、寬×高、長×高分別得到什么？是面積嗎？這里的關鍵是引導學生分步觀察，長×寬得到底面積為20 m2（如圖1），通過底面積我們可以想像出第一層的體積是20 m3（如圖2）。

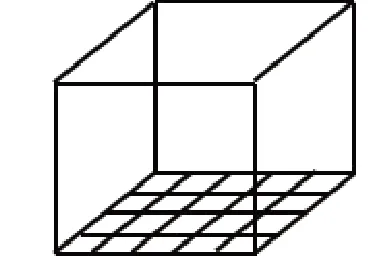
圖1

圖2

高是幾就有這樣的幾層，所以長×寬既可以表示底面積，也可以表示第一層的體積，于是用底面積×高可以得到長方體體積。有的學生還能從正面看，用正面的面積×寬也能求出體積；還可以從側面看，橫截面的面積×長也可以求出體積。對長方體體積公式深入理解之后，在教學“圓柱體的體積”時，學生的思考方式就會更加便捷，他們不用經(jīng)歷把圓柱轉化成長方體的全過程，而是想到算出底面積是多少，就可以知道第一層的體積是多少，高是幾就有這樣的幾層，直接用底面積×高，完美地實現(xiàn)了體積計算的遷移。

（三）把握數(shù)學思想設計核心問題

數(shù)學學科核心素養(yǎng)的培育離不開數(shù)學思想方法的滲透。學生只有掌握了解決問題的一般性思維策略，才能有效地解決具體問題。教師要善于挖掘教材中所蘊涵的數(shù)學思想和方法并滲透在教學中，引導學生去感悟和體驗。

如教學“數(shù)字編碼”時，很多教師設計的教學重點是讓學生了解編碼中每個數(shù)字所蘊涵的意義，而這不是編碼學習的數(shù)學價值。教師要把重點放在讓學生感受編碼的神奇上，使學生體會編碼的唯一性。所以，本節(jié)課應根據(jù)唯一性這個數(shù)學思想方法來設計核心問題：全國14億人口的身份證號碼會重復嗎？剛開始，很多學生認為一定會重復。接著，教師通過一個具體的身份證號碼，結合政區(qū)圖讓學生展開探索活動：35代表福建省，福建省有3689萬人口，說明只有3689萬人的身份證前兩位是一樣的。01代表福州市，福州市有589萬人，說明只有589萬人的身份證前四位是一樣的。81代表福清市，福清市有139萬人口，說明只有139萬人的身份證前6位是一樣的。根據(jù)出生年月日，福清市同年同月同日出生的人大約有437人，說明只有437個人的身份證前14位可能重復。通過三位的順序號可以把437個人的身份證號依次排列。所以，身份證號碼不會重復。通過這個過程，學生感到很神奇：14億人口居然能做到身份證不重復！這充分體現(xiàn)了數(shù)字編碼的唯一性。理解編碼的數(shù)學思想方法之后，學生在編學號的時候就會考慮如何提供有效信息讓學號不重復。

基于學生深度學習來設計核心問題，實現(xiàn)了數(shù)學學習從知識記憶轉變?yōu)閱栴}解決，促進了深度學習的發(fā)生和發(fā)展。