面向直升機抗墜毀的新型夾心八邊形蜂窩設計、仿真和理論研究

王佳銘，李志剛,*，梁方正，劉婉婷，廖就，陳芳育，李萌，邵特立

1.北京交通大學 機械與電子控制工程學院，北京 100044

2.中國直升機設計研究所，景德鎮 333001

3. 中國空間技術研究院 錢學森空間技術實驗室，北京 100094

4. 交控科技股份有限公司，北京 100070

蜂窩結構作為多孔結構的一種，由于其密度小、剛度低、壓縮變形大及變形可控等優點，現已成為一種理想的緩沖吸能結構，目前廣泛應用于汽車、軌道交通和航空航天等領域。在實際的工程應用中，很多實際場景對蜂窩的承載吸能能力要求很高，例如直升機的耐墜性設計等碰撞動能較大的相關領域，這些場合下需要具有更高吸能能力的新型蜂窩以在相同的安裝空間或同等質量條件下吸收更多的墜撞動能，保障乘客的生存空間。基于此，本文提出了一種相對于六邊形和正方形蜂窩結構吸能效果更好的新型蜂窩。

目前在對蜂窩結構的研究中，首先是理論層次的研究，國內外部分學者針對多種常用構型的蜂窩力學承載進行了理論模型的推導建立，其中榮吉利、Bai等給出了六邊形蜂窩軸向平臺應力的理論公式，為蜂窩結構緩沖設計提供理論依據。在蜂窩結構的尺寸參數影響方面，大部分學者通過仿真與試驗相結合的方式，對六邊形蜂窩胞元尺寸參數(邊長、壁厚等)以及蜂窩塊尺寸參數(長、寬、高)對蜂窩力學性能的影響展開研究。其中趙輝等研究表明蜂窩壓縮時平臺應力等力學性能指標與壁厚邊長比值正相關，徐天嬌、賈培奇等研究表明，面內尺寸及高度變化時，平臺應力沒有明顯的尺寸效應，但密實化應變對高度尺寸具有一定敏感性。此外，在蜂窩壓縮仿真方法的研究方面，歐陽昊、王永寧等發現殼單元有限元模型能準確反映鋁蜂窩逐步壓潰的變形模式，車全偉等也提出了一種合理的蜂窩壓縮仿真建模方法。

近些年來，有學者開始將研究聚焦在新型蜂窩結構的設計，以求獲得吸能效果更佳的蜂窩結構。何彬和李響提出了一種基于菱形和圓形的新型組合蜂窩，通過數值仿真與正六邊形、正方形、三角形、Kagome 蜂窩的中高速沖擊仿真結果進行了對比，發現新型組合蜂窩整體剛性和能量吸收能力較好。王中鋼和姚松對加筋型正六邊形蜂窩進行了軸向壓縮力學性能的研究，結果表明1.5 倍厚度加筋的蜂窩力學性能穩定，是最優的筋厚選擇方案。Yang等的研究表明，在傳統蜂窩結構基礎上引入馬蹄形結構或混合波紋結構后，蜂窩平臺應力和比吸能都有一定程度的增強，李萌等通過仿真試驗相結合的方式，發現串聯組合式鋁蜂窩緩沖器相較于單個鋁蜂窩緩沖器來說可以吸收更多能量。

本文基于正方形蜂窩和八邊形蜂窩提出了夾心八邊形新型構型蜂窩，首先通過六邊形蜂窩軸向壓縮試驗和仿真對比，驗證了蜂窩建模和仿真方法的正確性；然后建立了不同尺寸的八邊形蜂窩有限元模型并進行了變形模式和吸能的分析，并對夾心八邊形蜂窩和常用的六邊形蜂窩等進行了吸能能力的對比分析；最后建立了夾心八邊形蜂窩的理論模型并進行了仿真驗證，表明建立的理論模型對蜂窩的平臺應力以及相對密度具有很好的預測精度，為新型蜂窩緩沖結構的設計提供了依據。

1 夾心八邊形蜂窩設計

為了進一步提高蜂窩結構軸向吸能能力，本文設計了夾心八邊形蜂窩結構，以正八邊形蜂窩胞元為出發點，采用內嵌四邊形蜂窩以填充胞元內空隙，以合理的相對密度增加將新構型蜂窩的承載吸能效果更大化。正八邊形蜂窩胞元邊長為，內嵌四邊形蜂窩胞元邊長為，并在之間添加肋板連接形成夾心八邊形蜂窩，整個結構的壁厚均為，陣列獲得最后所需結構，其中標紅部分為該構型的一個基本可重復單元，如圖1所示。

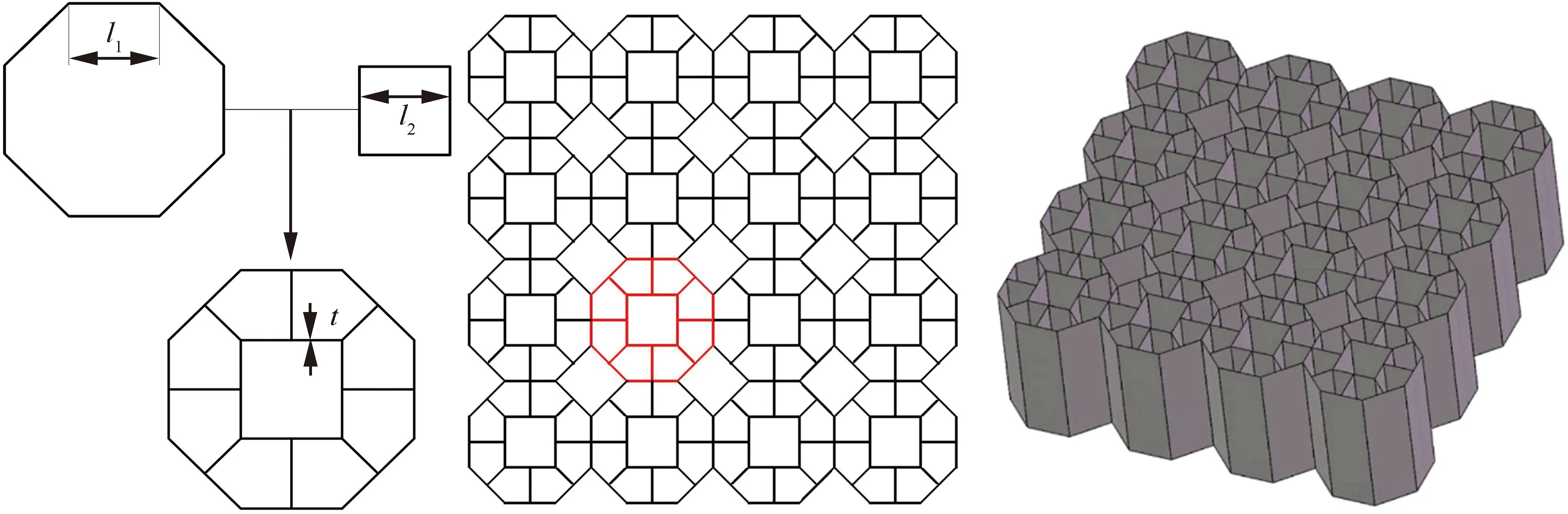
圖1 夾心八邊形蜂窩設計Fig.1 Design of cored octagon honeycomb

2 夾心八邊形蜂窩理論模型

考慮到通過仿真或者試驗的方式來研究夾心八邊形蜂窩承載能力計算周期較長，因此本節將建立夾心八邊形蜂窩軸向承載時的平臺應力的理論模型以快速預測該構型軸向壓縮時平臺應力等吸能指標隨參數的變化規律。

2.1 平臺應力理論模型

蜂窩在承受軸向壓縮時，經歷3個階段，首先是線彈性區域，應力隨應變線性變化，且快速增加至初始峰值應力；然后是平臺區域，應力值圍繞平臺應力上下波動；最后是密實化變形區域，應力從密實點快速上升，進入密實化階段。其中平臺區通過發生周期性的折疊變形吸收能量，是蜂窩吸能緩沖的最重要階段，通常占據蜂窩整體吸能的80%以上。平臺應力是表征蜂窩結構吸能特性的一個重要指標。因此，本文推導建立了夾心八邊形蜂窩平臺應力的理論模型。本文提取圖1中所示的夾心八邊形蜂窩結構的一個基本單元進行分析以建立夾心八邊形蜂窩的平臺應力理論模型。根據Chen和Wierzbicki提出的超簡化折疊單元理論，認為在其變形過程中，變形能由鉸鏈屈曲吸能和膜延展吸能兩部分組成。簡化后的基本折疊單元如圖2所示。

以一個塑性鉸波長為2高的十字胞元為例，根據系統的能量守恒有

·2=+

(1)

式中：為平均壓潰力；為鉸鏈屈曲吸能；為膜延展吸能。

鉸鏈屈曲吸能表示所有塑性鉸鏈線彎曲變形能量總和。每個折疊單元由3條塑性鉸線組成，如圖2(a)所示，3條水平塑性靜態絞線分別位于基本折疊單元的兩側和對折線上，相應旋轉角度為π/2、π/2、π， 因此彎曲吸能可以表示為

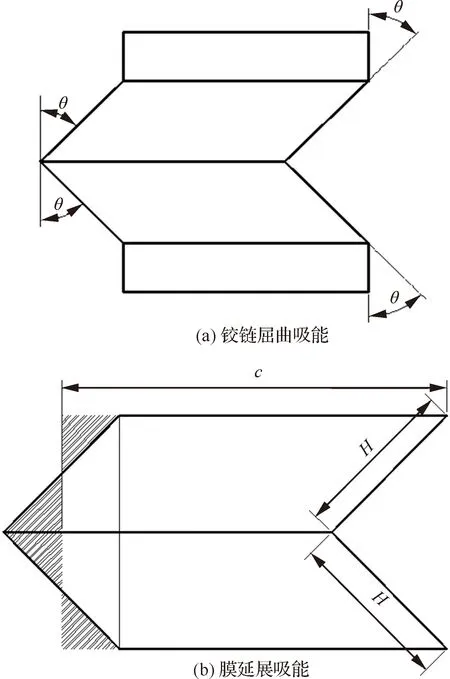
圖2 超簡化折疊單元Fig.2 Simplified super folding element

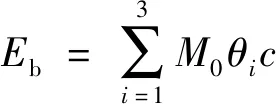
(2)

式中：為厚度為單元的全塑性彎矩；為每條絞線的旋轉角度；為圖2(b)中每條絞線的長度。對于厚度為的單元，=4，為流動應力，具體計算式為

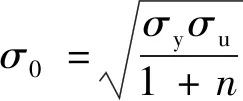
(3)

其中：為屈服應力；為極限應力；為材料硬化常數，取值為0.07。

將各變量代入式(2)計算得到夾心八邊形蜂窩的鉸鏈屈曲吸能為

=2π

(4)

式中：為夾心八邊形蜂窩所有胞壁的二維截面長度。

為了分析夾心八邊形蜂窩軸向壓縮時的膜延展吸能，將其截面劃分為3種基本單元：角單元、Ⅰ型三面板單元和Ⅱ型三面板單元，如圖3所示。這3種基本單元的膜延展吸能是通過對圖2(b)中陰影區域進行積分得到的。

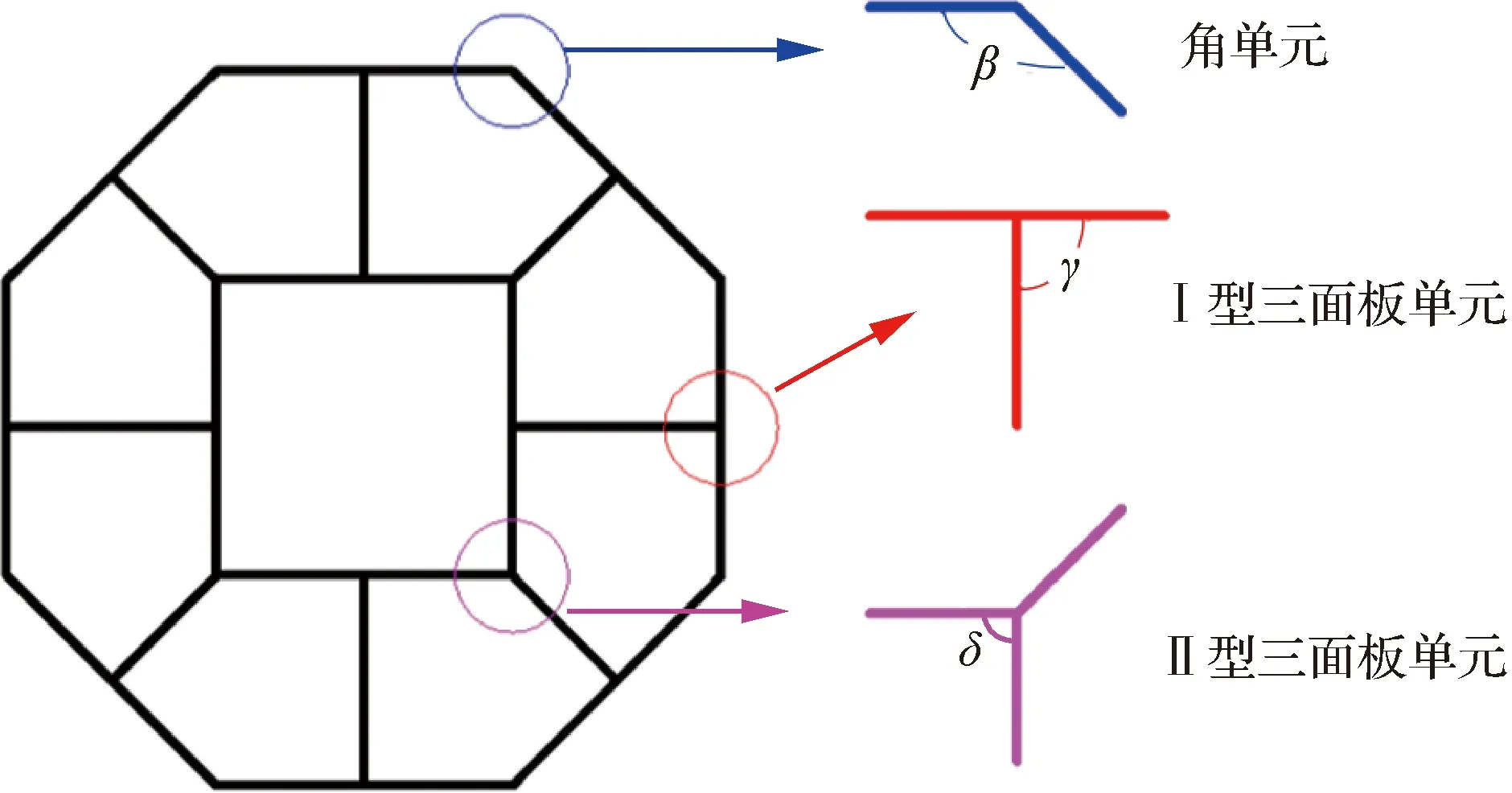
圖3 夾心八邊形蜂窩截面的吸能單元劃分Fig.3 Division of energy absorption unit of cored octagon honeycomb cross-section

根據文獻[5]對兩面板角單元的研究結果，通過對角單元拉伸和壓縮區域進行積分獲得膜延展吸能，計算式為

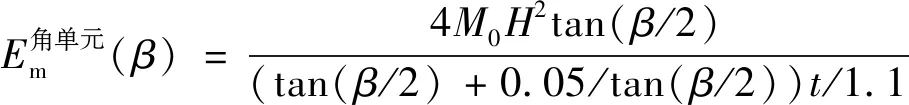
(5)

一個折疊波長高度的Ⅰ型三面板單元如圖4(a) 所示。設對稱面板的兩個相同角度為，三面板單元的膜延展吸能應該包括一個兩面板角單元和附加面板的膜延展吸能兩部分，根據圖4(b) 所示的附加面板的塌陷變形，三角形通過路徑延展為三角形，文獻[4]研究結果表明，附加面板的變化過程可簡化為

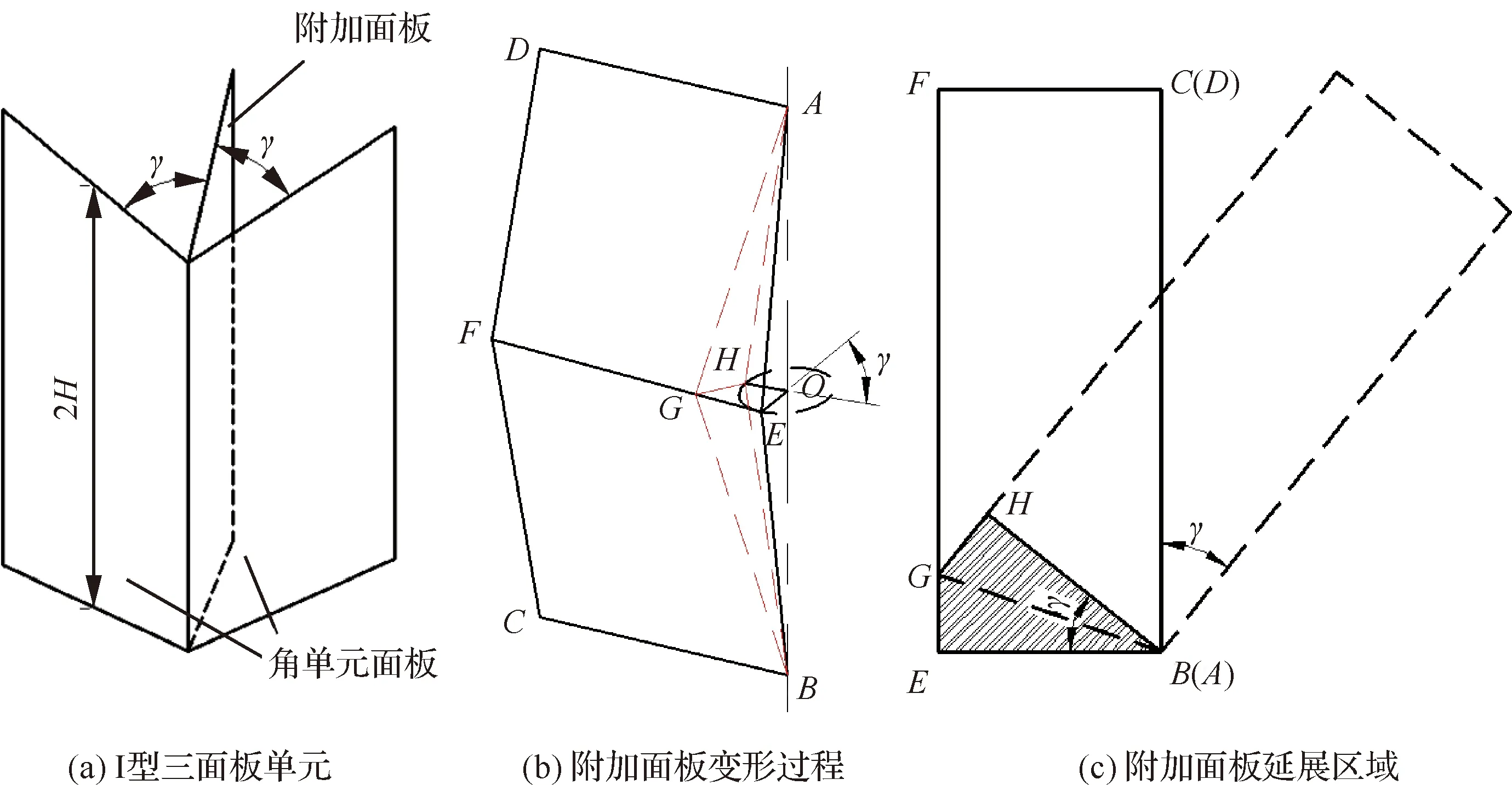
圖4 Ⅰ型三面板單元變形過程Fig.4 Deformation process of three-panel angular element Ⅰ

圖4(c)所示，兩個陰影三角形區域被定義為拉伸區域，對其進行積分可以得到附加面板的膜延展吸能，表達式為

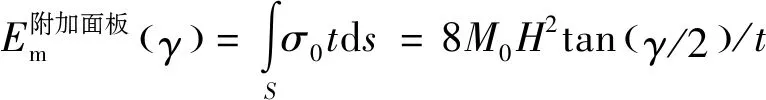
(6)

式中：為陰影部分的面積。

根據式(5)和式(6)(此處2相當于)的計算結果，Ⅰ型三面板單元的膜延展吸能為

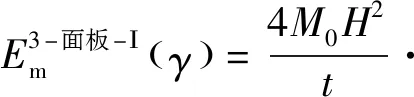
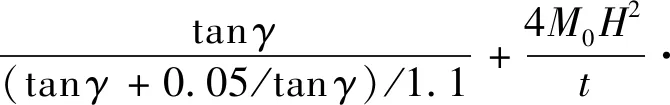
2tan (2)

(7)

與Ⅰ型三面板單元類似，Ⅱ型三面板單元的膜延展吸能同樣通過對每個面板的延展區域進行積分得到，圖5所示為夾角為的Ⅱ型三面板單元的理想折疊模型，將三面板單元分成1、2、3這3個面板，文獻[5]的研究結果表明，1號面板只受彎曲但無拉伸變形，因此其膜能為0，面板2的變形模式與Ⅰ型三面板單元中的附加面板相同；3號面板被拉伸，通過對圖5所示的藍色陰影區域進行積分得到3號面板的膜延展吸能，2號和3號面板膜延展吸能計算式分別為

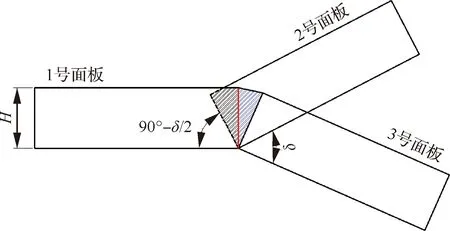
圖5 Ⅱ型三面板單元變形過程Fig.5 Deformation process of three-panel angular element Ⅱ

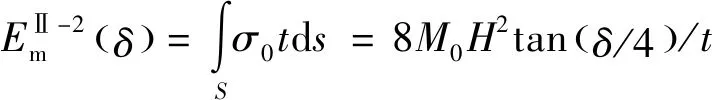
(8)

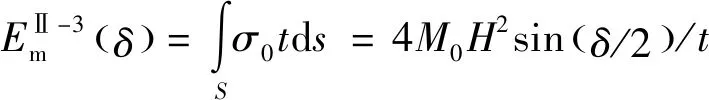
(9)

除了3個面板的延展吸能之外，Ⅱ型三面板單元變形中還存在面板厚度收縮變形導致的膜延展吸能，該部分計算表達式為

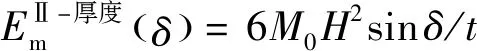
(10)

根據式(8)～式(10)的計算結果，Ⅱ型三面板單元總的膜延展吸能為

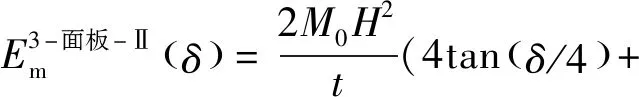
2sin(2)+3sin)

(11)

由圖3可以看出，一個夾心八邊形代表性單元包括8個=135°的角單元、12個=90°的I型三面板單元和4個=90°的Ⅱ型三面板單元，因此，總的膜延展吸能為

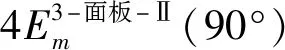
(12)

將式(12)和式(4)代入式(1)，則可得

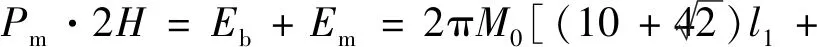
(13)

根據折疊波長使平均載荷取最小值條件有：δδ=0，則

(14)

則夾心八邊形蜂窩的平均載荷可以表示為

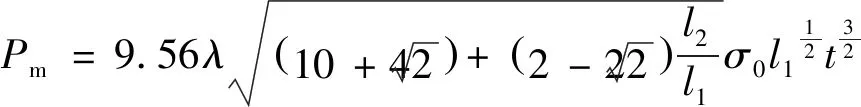
(15)

考慮到鋁蜂窩動態壓縮下的慣性效應，引入動態增強系數，對于鋁，該系數一般取值范圍為1.1～1.6，本文取值為1.2。

為減少同種規格蜂窩因外形尺寸不同對平均載荷的影響，本文以平臺應力代替平均載荷來表示夾心八邊形鋁蜂窩軸向吸能特性，可表示為

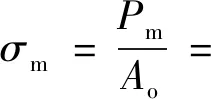
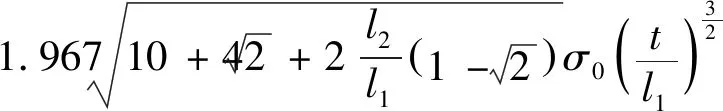
(16)

式中：為夾心八邊形胞元的面積。

根據式(16)可以看出，夾心八邊形蜂窩的平臺應力與壁厚邊長比值的3/2次方成正比。

2.2 八邊形邊長與內嵌四邊形邊長比對蜂窩相對密度和平臺應力的影響

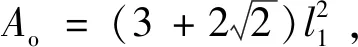
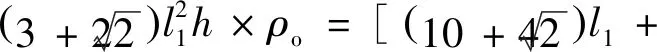
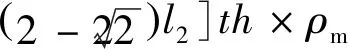
(17)

式中：為蜂窩基體材料的密度。因此夾心八邊形蜂窩結構的相對密度為

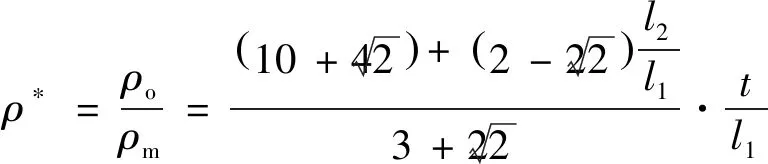
(18)

由式(16)和式(18)可以看出，蜂窩的相對密度和平臺應力是蜂窩壁厚、外部八邊形邊長以及內部四邊形與外部八邊形邊長比值的函數。當壁厚確定時，并且和的相對比例確定時，模型的整體結構確定。此時相對密度以及平臺應力的值主要取決于外部八邊形胞元邊長。可以看到，隨著的增加，相對密度以及平臺應力都會降低。

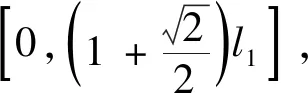
3 夾心八邊形蜂窩軸向壓縮仿真

3.1 蜂窩軸向壓縮仿真方法驗證

由于本文新設計的夾心八邊形蜂窩結構尚未加工制作，而文獻中也沒有該類蜂窩結構的試驗數據，為了驗證本部分建立的夾心八邊形蜂窩有限元模型的有效性，本文將通過對常規的六邊形蜂窩進行仿真分析和軸向壓縮試驗，通過仿真與試驗的對比以間接驗證模型建立和仿真方法的正確性，驗證之后，可靠的模型建立和仿真的通用方法可以用于本文設計的夾心八邊形蜂窩的軸向壓縮仿真和吸能評估。

本試驗中所用的蜂窩胞元和樣品蜂窩結構如圖6所示，其中蜂窩胞元短邊長=6 mm，長邊長=10.4 mm，夾角=120°，壁厚=0.045 mm，相對密度為0.006。蜂窩試件為長和寬為77 mm、高度為36 mm的長方體試件，統一采用線切割方式進行加工。通過壓縮試驗機進行試驗，設置試驗機壓頭速度為0.36 m/s，對應的應變率為10 s，采集得到力-位移曲線，然后分別根據蜂窩截面尺寸和軸向壓縮高度尺寸將力-位移曲線換算為應力-應變曲線。

圖6 蜂窩壓縮試驗細節Fig.6 Details of honeycomb compression test

基于HyperMesh和LS-DYNA建立的軸向壓縮鋁蜂窩模型如圖7所示，根據試驗工況，將蜂窩置于兩剛性平板之間，下部剛性平板完全固定，模擬支撐平臺，上部剛性平板以恒定速度下壓。兩端剛性板與蜂窩之間設置為自動面-面接觸，蜂窩自身設置為自接觸。設置鋁蜂窩自身接觸摩擦系數為0.3，鋁蜂窩與剛性隔板之間的摩擦系數為0.1。蜂窩結構采用殼單元進行建模，在殼單元厚度方向設置5個積分點。為了分析網格尺寸對仿真結果的影響，采用1、0.5、0.3、0.2 mm 尺寸的網格進行網格收斂性分析，分析發現網格尺寸對仿真結果有一定的影響，在網格大小為0.3 mm 時，計算結果收斂。綜合考慮仿真計算精度和模型計算時間，采用大小為0.3 mm四邊形殼單元作為最終網格進行網格劃分。

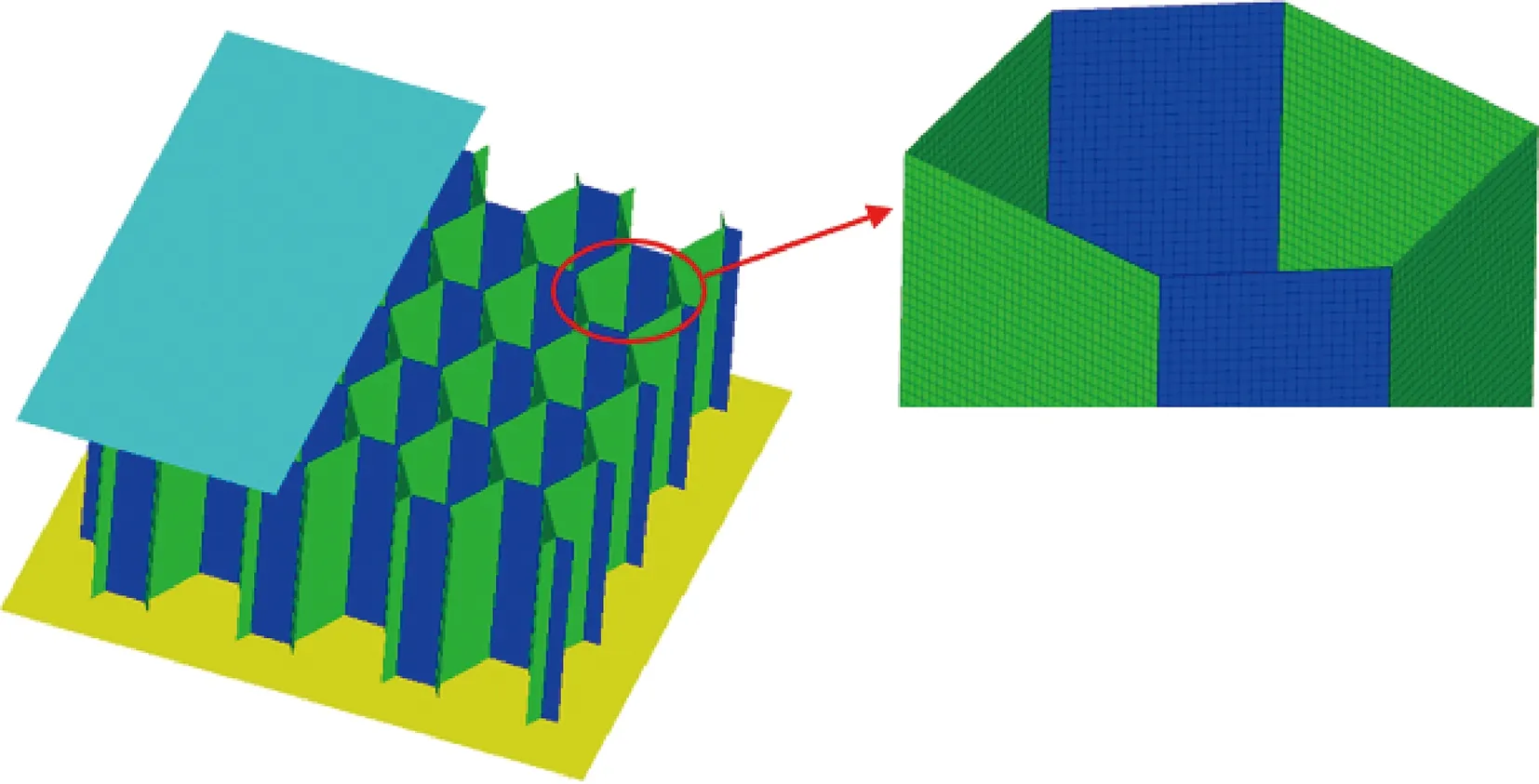
圖7 六邊形蜂窩有限元模型Fig.7 Finite element model of hexagon honeycomb

蜂窩材料采用多段線性彈塑性模型(MAT24)進行模擬，鋁蜂窩材料參數通過對鋁蜂窩鋁箔基體材料進行試驗獲得，具體的參數結果如表1所示。

表1 鋁蜂窩基體材料參數Table 1 Material parameters of aluminum honeycomb

仿真與試驗應力-應變曲線的對比和蜂窩變形過程如圖8(a)所示，可以看出，壓縮過程中，胞壁向下屈曲，褶皺從加載端開始逐個形成，逐次保持到密實化狀態，與試驗保持一致。但是可以看到，仿真結果與試驗數據吻合較好，初始峰值相等，平臺段應力值大小相符。除此之外，為了進一步驗證模型，本文使用文獻[22]中3003鋁蜂窩在10 m/s壓縮速度工況下的試驗數據進行了仿真驗證，建模的蜂窩尺寸和材料參數均與文獻[22]保持一致。10 m/s壓縮速度工況下的仿真應力應變曲線與文獻[22]中給出的平臺應力值如圖8(b) 所示，仿真平臺應力與文獻中試驗數據僅存在5%的誤差，一致性較好，進一步驗證了仿真方法的正確性。綜合上述兩部分的試驗驗證，說明該仿真模型具有較好的精度，驗證了建模和仿真方法的正確性，可以用于下一步夾心八邊形蜂窩的仿真和承載吸能評估。

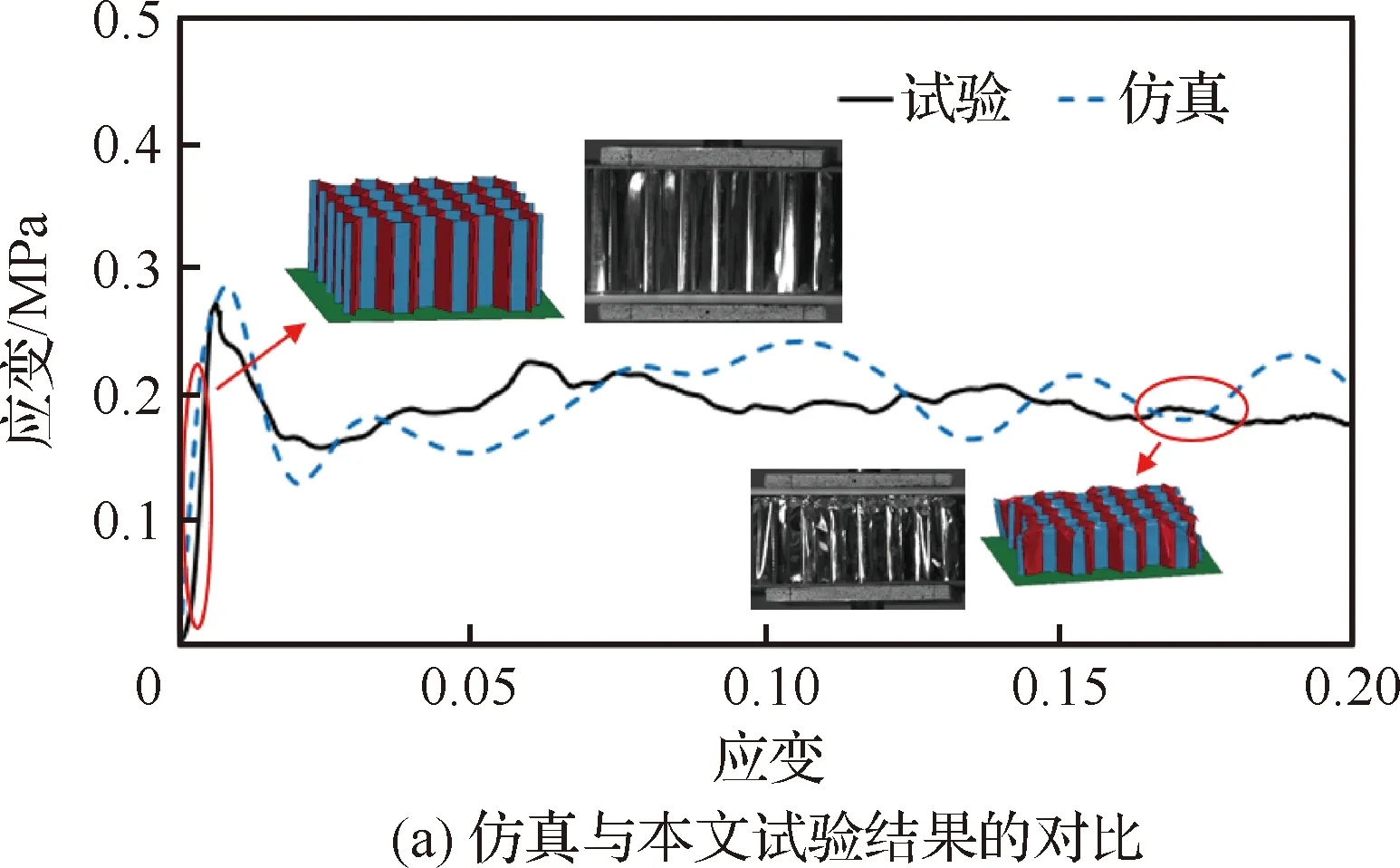
圖8 蜂窩壓縮應力-應變曲線的仿真和試驗結果對比Fig.8 Comparison of honeycomb compressive stress-strain curves between experimental and simulation results

3.2 夾心八邊形蜂窩仿真分析及理論模型驗證

在仿真模型和建模方法經過準確性驗證的基礎上，依據3.1節所述建模方法建立夾心八邊形蜂窩的軸向壓縮仿真模型，如圖9所示。

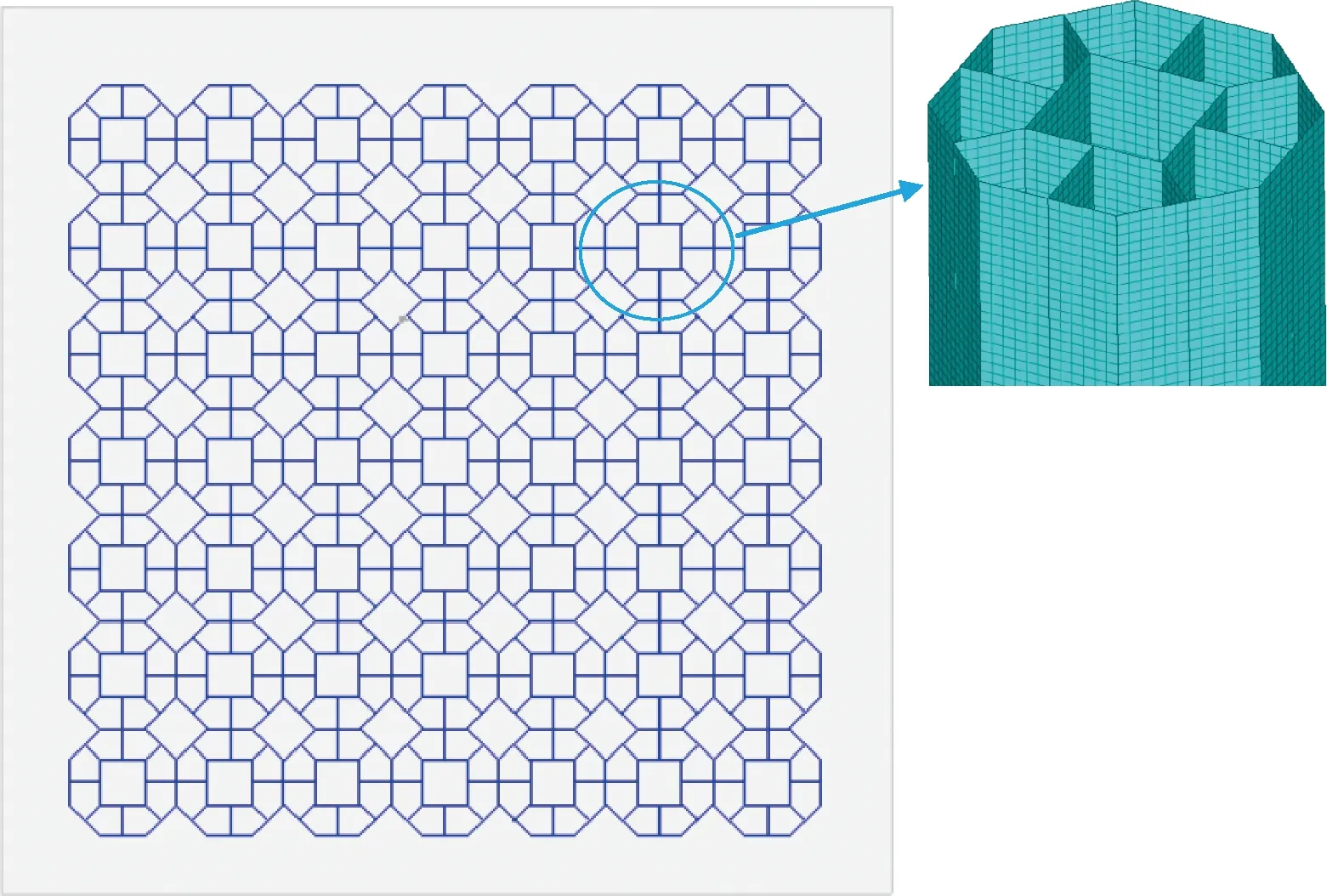
圖9 夾心八邊形蜂窩有限元模型Fig.9 Finite element model of cored octagon honeycomb

夾心八邊形蜂窩軸向壓縮變形如圖10所示。可以看出，夾心八邊形蜂窩軸向壓縮的變形模式依然與六邊形蜂窩類似，首先位于底部的胞壁首先發生彎曲變形，模型整體向下形成規則的褶皺變形，逐步壓潰進入密實段。由于內嵌四邊形蜂窩填充了八邊形蜂窩的內部空隙，兩者中間的肋板通過發生彎曲變形，同時限制了外部八邊形蜂窩和內嵌四邊形蜂窩豎直胞壁的規則折疊變形，這樣就會導致夾心八邊形結構的軸向承載力提高，達到了在有限的空間內提升吸能能力的設計目的。

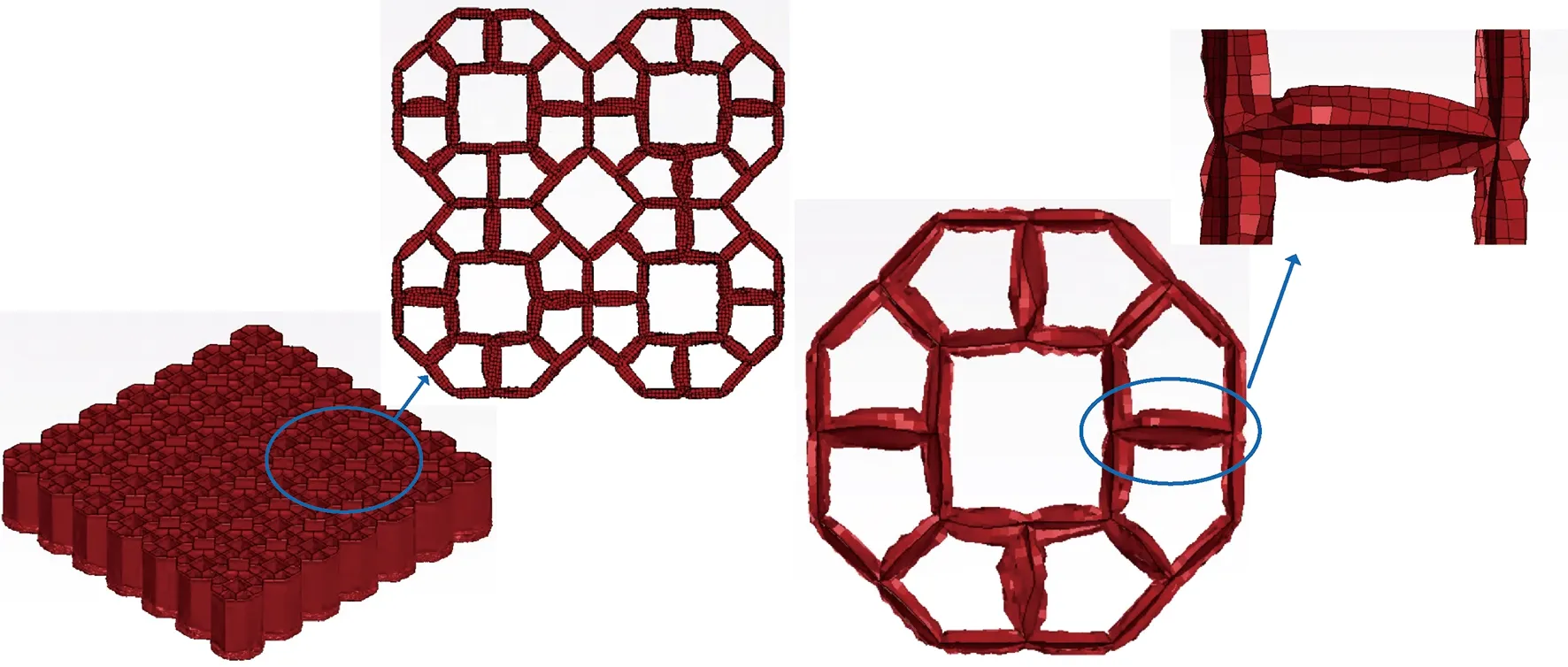
圖10 夾心八邊形蜂窩變形模式Fig.10 Deformation mode of cored octagon honeycomb

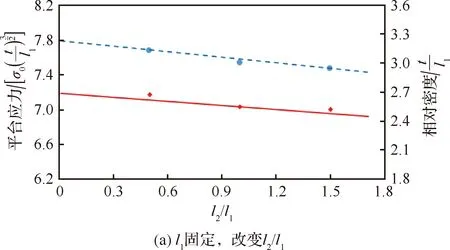
圖11 夾心八邊形蜂窩平臺應力及相對密度隨邊長的變化趨勢Fig.11 Variation trend of platform stress and relative density with side length for cored octagon honeycomb

此外，本文對不同、值以及不同壁厚的夾心八邊形蜂窩進行了仿真計算，平臺應力以及相對密度的理論模型與仿真結果的對比如表2所示。可以看出，理論公式推導結果與仿真結果誤差在5%以內，理論模型具有較高的精度。

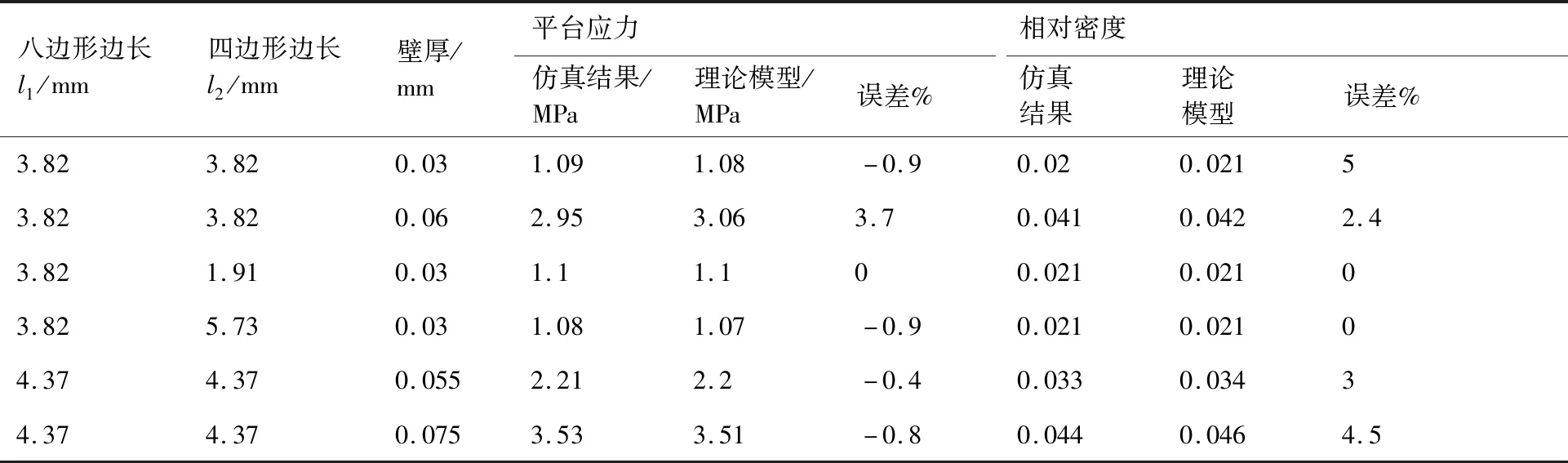
表2 理論模型與仿真結果對比Table 2 Comparison of theoretical model and simulation results

3.3 夾心八邊形蜂窩與其他典型蜂窩結構吸能能力的對比分析

本節通過比吸能和平臺應力兩個重要的吸能評估指標來評估夾心八邊形蜂窩的吸能能力，其中比吸能(SEA)是評價不同材料或結構在壓潰過程中能量吸收能力的重要指標。質量比吸能和體積比吸能的計算表達式為

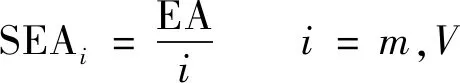
(19)

式中：EA為蜂窩壓潰過程中總吸收能量，對于不同的蜂窩結構，不同密實程度的吸收能量不同，本文考慮的總吸能是指蜂窩從初始壓縮時刻至蜂窩密實化階段開始時刻為止；為蜂窩質量；為蜂窩的體積。顯然比吸能越大，代表蜂窩吸能能力越好。

平臺應力()作為評估蜂窩壓潰過程中吸收能量的關鍵參數，將載荷位移曲線按照2.1節所述轉化為應力應變曲線后，計算表達式為

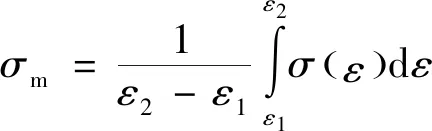
(20)

式中：和分別表示蜂窩軸向承載時平臺段的起始和終止應變。

對于不同的蜂窩構型，考慮到不同尺寸參數對承載能力的影響不同，因此本文為橫向比較夾心八邊形蜂窩的軸向承載能力，引入相同控制條件下的六邊形、正方形等常用蜂窩構型。

考慮到蜂窩結構在實際應用時通常會面臨安裝體積或質量要求更為苛刻的不同情況，出于不同考慮，本文引入了兩種不同的控制條件。第一種控制條件下，考慮到蜂窩吸能的重要指標平臺應力主要取決于壁厚與邊長的比值。因此，首先保證各個構型的壁厚邊長比值相等。并且在建模過程中保證蜂窩單個胞元的橫截面積相等，蜂窩結構高度均為30 mm，模型所含完整胞元數目一致，此種控制條件可以有效評估不同構型蜂窩在安裝空間更為有限的情況下吸能的效果，不同構型蜂窩的尺寸及模型信息如表3所示。

此外為了評估不同構型蜂窩在質量要求更為苛刻的情況下的承載能力，第二種控制條件下保證不同的蜂窩構型相對密度一致。對于不同的蜂窩構型，相對密度與胞孔尺寸間的關系不一致，相對密度不同會導致力學性能存在差異。本文控制不同蜂窩相對密度均為0.02，壁厚為0.03 mm，此時不同構型蜂窩的尺寸及模型信息如表4所示。

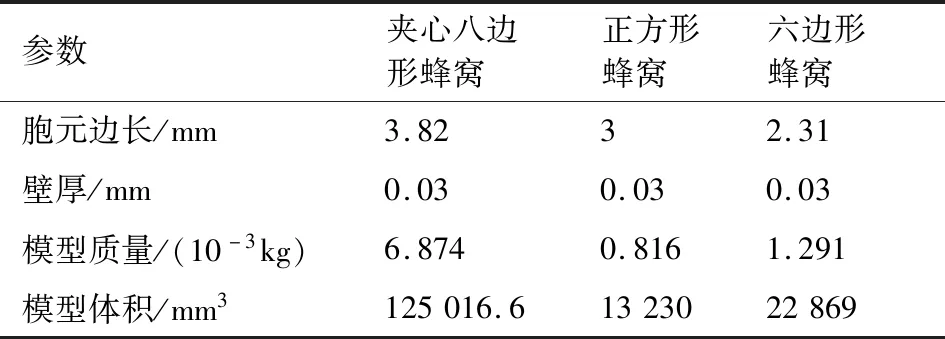
表4 相對密度一致時不同構型蜂窩的尺寸及模型信息Table 4 Geometric information of different honeycombs with same relative density

按照前面所述指標的計算，在上述兩種情況下，不同構型蜂窩的質量及體積比吸能和平臺應力的結果對比如圖12及圖13所示。可以看出，在胞元橫截面積一致且壁厚與邊長比值固定的情況下，新提出的夾心八邊形蜂窩均大幅度領先于六邊形和正方形蜂窩，體積比吸能和平臺應力甚至達到了六邊形蜂窩的兩倍以上。這就意味著如果實際安裝空間有限，對于蜂窩安裝體積要求很苛刻的情況下，本文提出的夾心八邊形新型蜂窩可以在有限的體積內起到更好的緩沖吸能效果。而在控制相對密度一致時，夾心八邊形蜂窩的3個指標均與最常用的六邊形蜂窩持平，承受軸向壓縮時可以起到較好的吸能效果，且均優于正方形蜂窩。這意味著夾心八邊形蜂窩在安裝質量要求苛刻的環境下也能表現出較好的緩沖吸能效果。綜合來看，本文新提出的夾心八邊形蜂窩的軸向壓縮吸能優于目前應用廣泛的六邊形和正方形蜂窩，而且更適合應用在安裝體積苛刻的實際使用環境下，是一種吸能效果良好的新構型蜂窩。

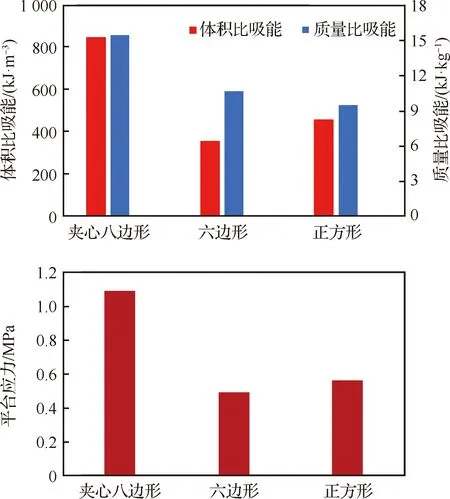
圖12 壁厚邊長比值相同情況下不同蜂窩承載和吸能對比Fig.12 Comparison of load-carrying and energy absorption ability for different honeycombs with same wall thickness to side length

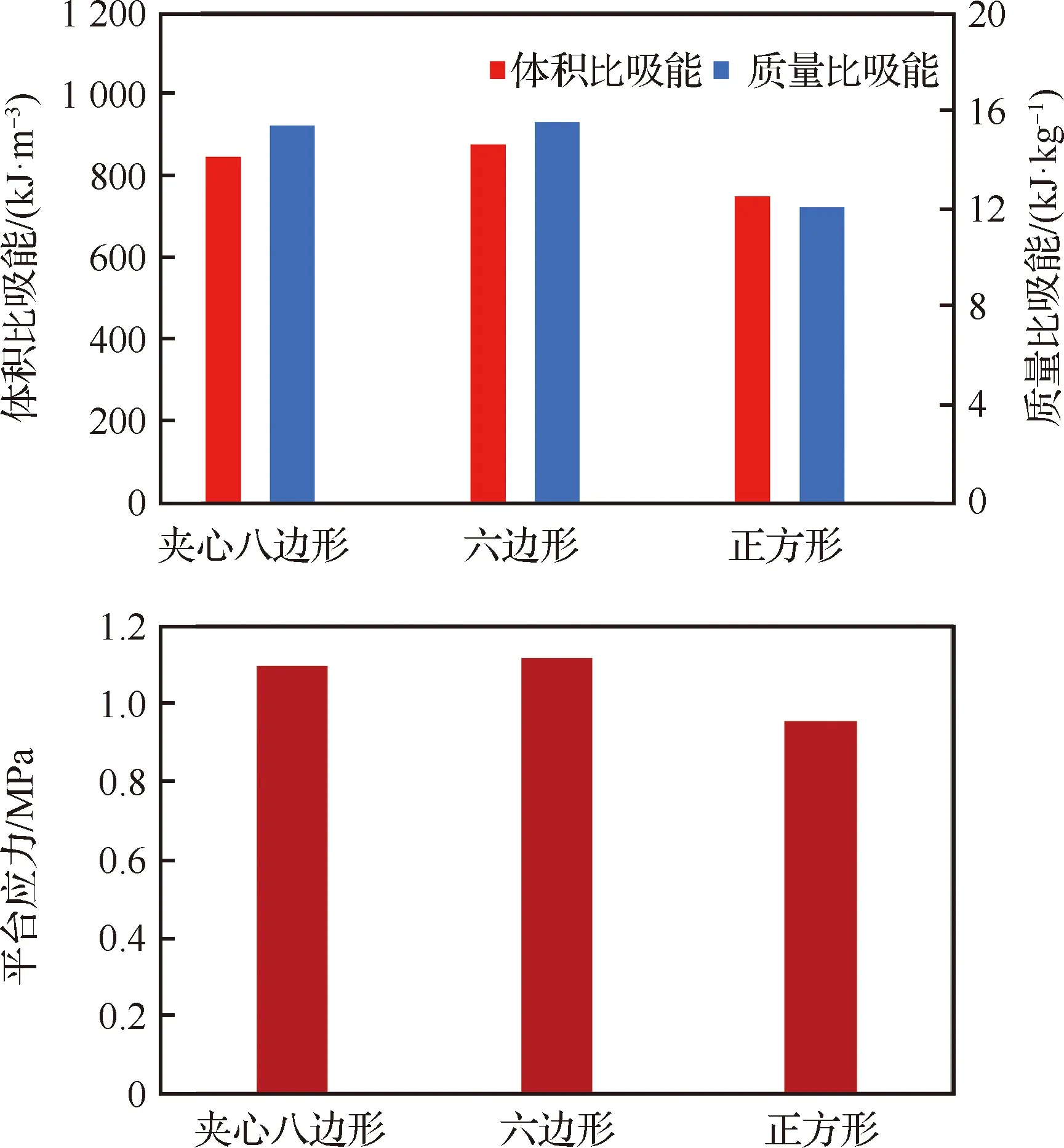
圖13 相對密度相同情況下不同蜂窩承載和吸能對比Fig.13 Comparison of load-carrying and energy absorption ability for different honeycombs with same relative density

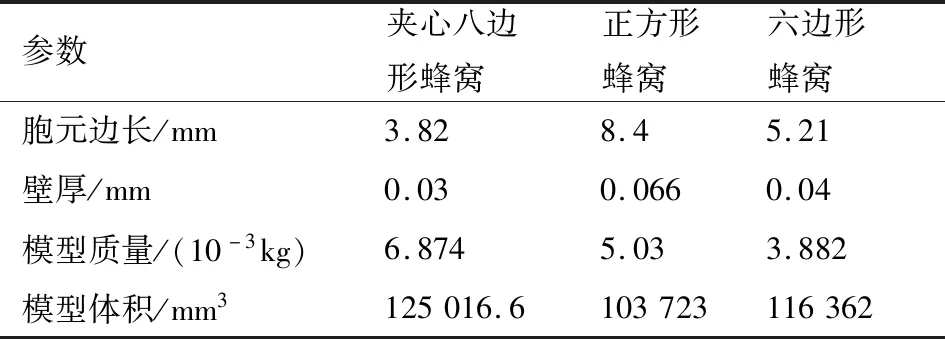
表3 壁厚邊長比值一致時不同構型蜂窩的尺寸及模型信息Table 3 Geometric information of different honeycombs with same ratio of wall thickness to side length

4 夾心八邊形蜂窩在直升機駕駛艙抗墜毀設計中的應用

本文以某型號直升機結構為建模依據，建立了簡化后的直升機駕駛艙垂向跌落有限元模型來評估夾心八邊形蜂窩填充駕駛艙底艙時的吸能效果。該模型由蒙皮、長桁、隔框、底板、橫梁、縱梁、支撐板件以及剛性墻組成，有限元模型如圖14所示。由于該模型不包括直升機起落架、抗墜毀座椅等直升機墜落時的關鍵承載結構，因此本節只能在同一條件下定性比較夾心八邊形蜂窩相較六邊形蜂窩的吸能能力。

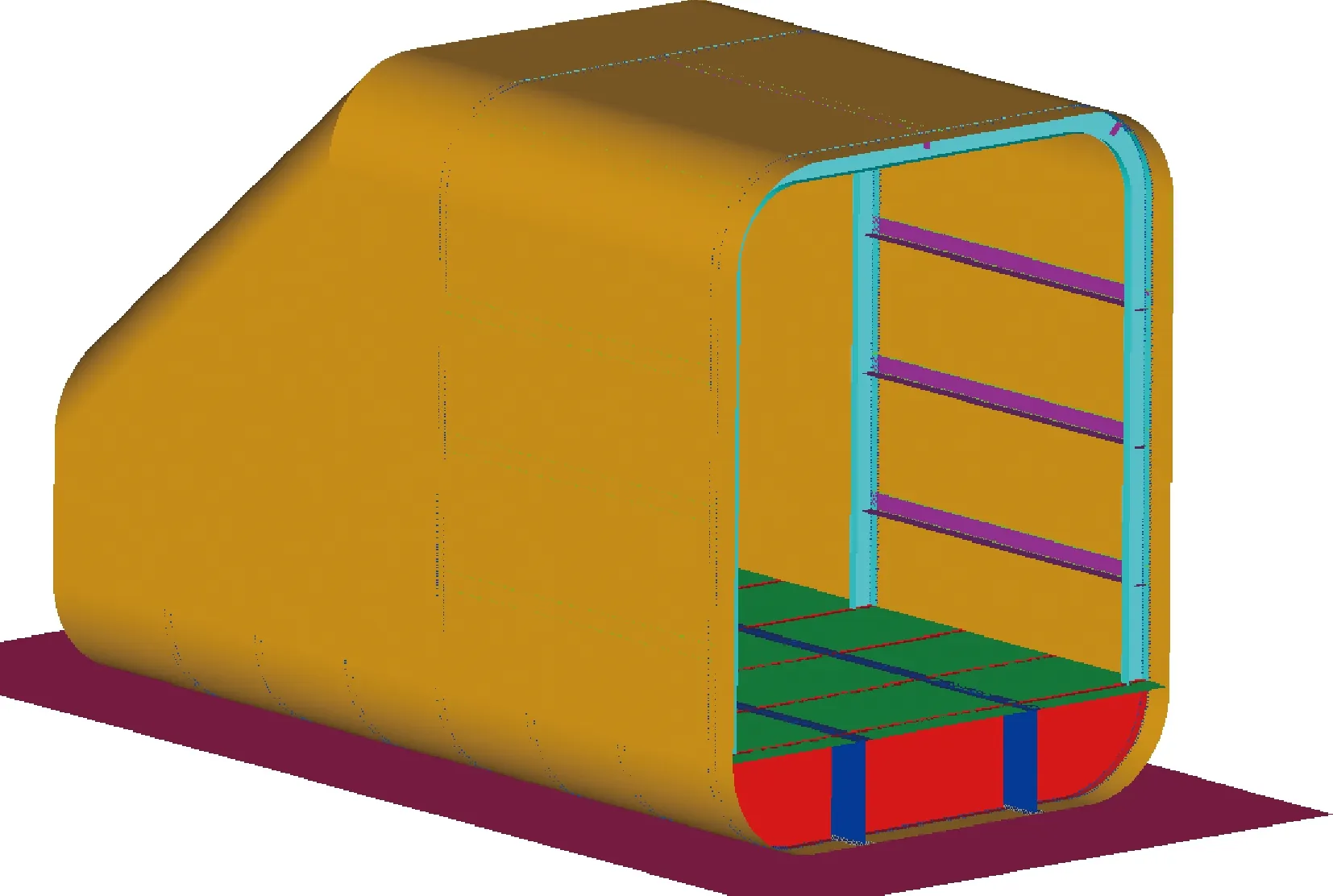
圖14 直升機駕駛艙有限元模型Fig.14 Finite element model of helicopter cockpit

駕駛艙結構均為鋁合金材料，采用MAT24本構進行模擬，統一采用四節點殼單元進行網格劃分。整個模型共有429 908個節點，420 785個單元，總質量為2 019.2 kg。為了評估夾心八邊形蜂窩的承載能力，在駕駛艙底部的橫縱梁交接位置放入等體積的相同壁厚邊長比值下的夾心八邊形蜂窩或者六邊形蜂窩來對比沒有蜂窩承載時的情況。考慮到直接采用真實蜂窩模型與駕駛艙模型進行耦合仿真時，兩者網格尺寸相差很大導致計算時間過長，因此采用等效實體塊建模的方式來建立蜂窩模型。等效蜂窩模型采用MAT126(MAT_MODIFIED_HONEYCOMB)本構進行模擬，將仿真得到的夾心八邊形蜂窩以及六邊形蜂窩的異面壓縮應力應變曲線作為輸入，在3個方向上指定相同的非線性彈塑性行為來將蜂窩近似為各向同性模型以評估其在駕駛艙跌落中的承載能力。該本構的楊氏模量從未開始壓縮狀態到壓實狀態隨體積應變變化而線性變化，具體的材料參數如表5所示。

表5 蜂窩等效模型材料參數匯總Table 5 Summary of honeycomb equivalent model material parameters

該有限元模型各部分的連接關系為:長桁、隔框、底板橫縱梁等內部結構采用共節點接觸，長桁、隔框、橫縱梁等均與外部蒙皮采用MAT100 Spotweld焊點連接。駕駛艙模型整體采用自接觸，并且與剛性墻之間采用自動面面接觸。底部剛性墻采用完全固定約束，對駕駛艙模型施加大小為10 m/s的初始跌落速度以模擬駕駛艙低空垂向跌落工況。通過機艙底板的最大過載及最大變形量以及碰撞跌落過程中各個承載部件的吸能信息來定性評估夾心八邊形蜂窩在直升機駕駛艙低空墜落工況下的吸能效果。

無蜂窩、置入六邊形蜂窩、置入新型夾心八邊形蜂窩3種情況下的直升機駕駛艙跌落仿真結果分別如圖15(a)～圖15(c)所示。可以看出，從圖15(a)～圖15(c)底艙變形量逐漸減小。對于該模型來說，駕駛艙后半部分為駕駛員乘坐位置，該部分為人員保護的關鍵區域，底板對應的最大變形量及過載結果如圖16(a)所示，跌落過程中各個部件的吸能量如圖16(b)所示。結果表明無蜂窩緩沖結構時，直升機底艙基本完全壓潰，橫縱梁作為主承載部件在該過程中通過塑性變形吸收了大量的碰撞動能，底艙最大變形量為219.5 mm，底板的最大過載為88.9(為重力加速度)。在置入蜂窩后，無論是六邊形蜂窩還是新型夾心八邊形蜂窩，都大大減少了底艙的變形量，底板的最大過載也得到有效的縮小。蜂窩結構在壓潰過程中吸收了大部分碰撞動能，駕駛艙原有結構部分的吸能得到降低。這就意味著蜂窩部件的加入大大緩解了駕駛艙原有結構的承載壓力，可以降低橫縱梁等原有承載結構的設計要求。結果表明，同壁厚邊長比值下的六邊形蜂窩吸能能力相對較弱，底艙的最大變形量減少至181.4 mm，底板的最大過載減小至66.1。進一步比較六邊形和夾心八邊形蜂窩的吸能能力，可以看出，等體積下的夾心八邊形蜂窩吸能效果更加，吸能量是六邊形蜂窩的1.9倍，這與3.3節結論一致。此外，夾心八邊形蜂窩的底板最大過載以及最大變形量得到大幅縮小，最大過載僅為54，最大變形量僅有140.3 mm，大大保護了內部乘客的生存空間。可以看出，本文新設計的夾心八邊形蜂窩相較目前應用廣泛的六邊形蜂窩更加適用于直升機底艙耐墜性設計等對吸能要求較高的工況。

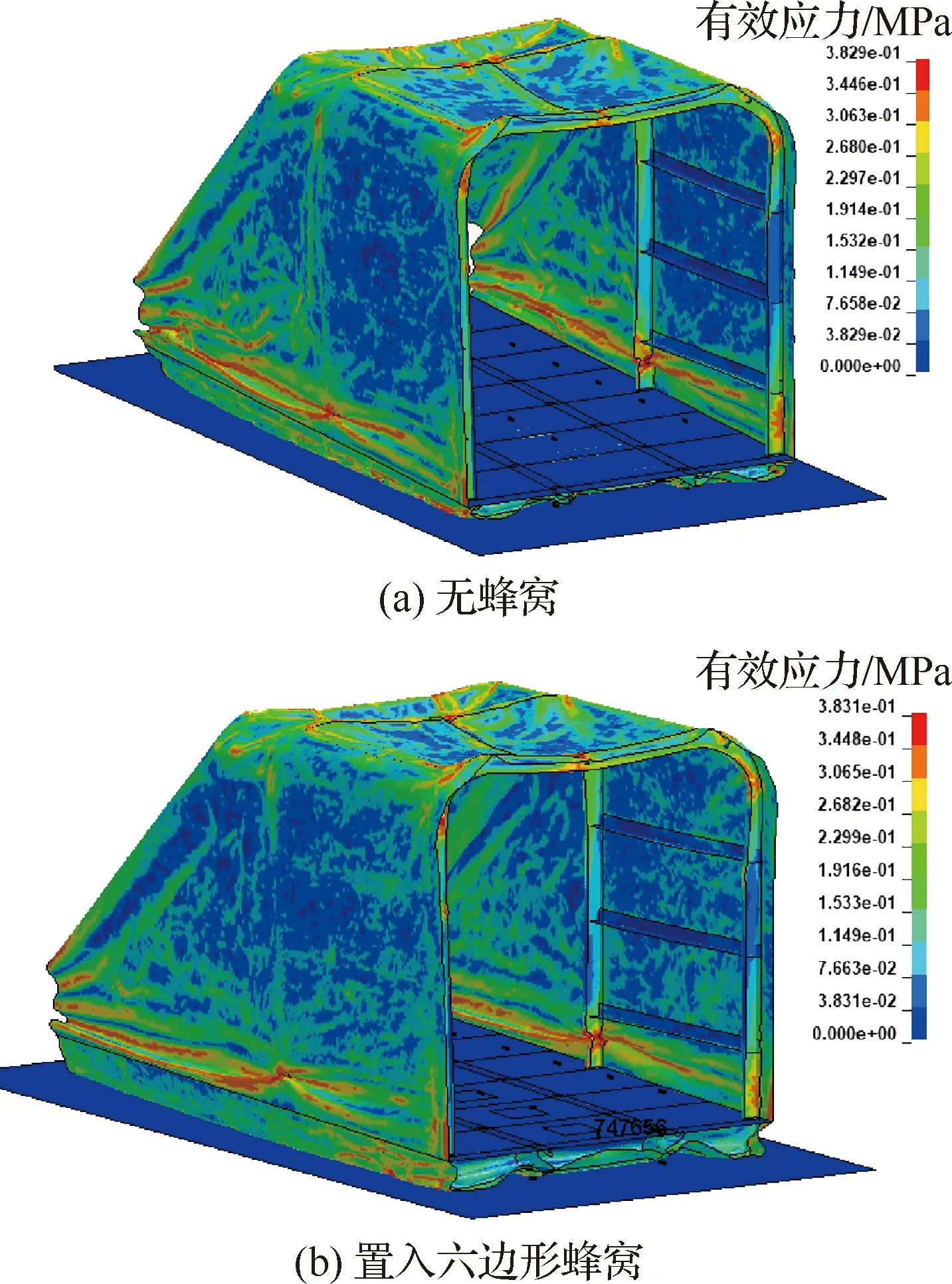
圖15 駕駛艙跌落仿真結果Fig.15 Drop simulation results of cockpit

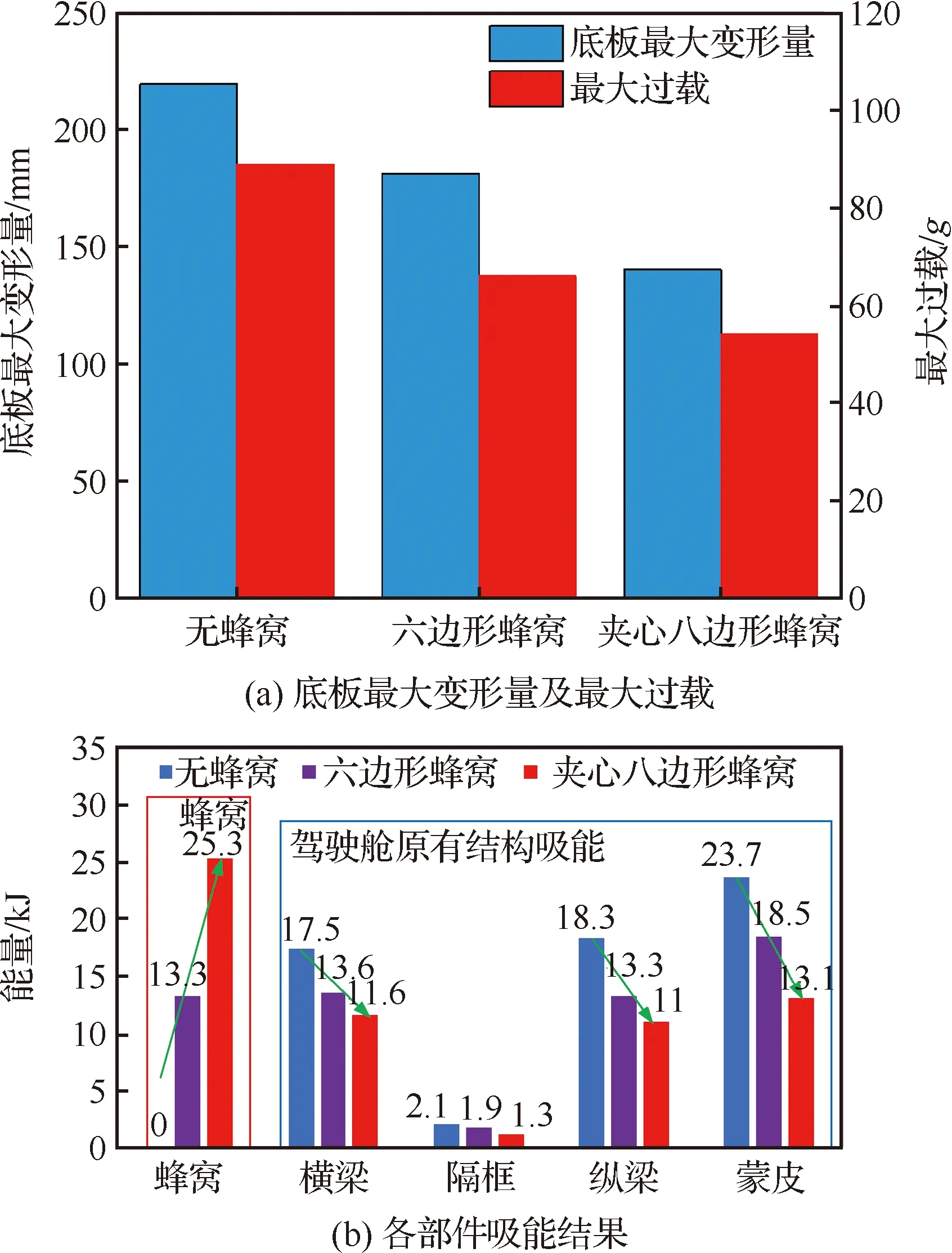
圖16 底板變形結果及各部件吸能結果Fig.16 Deformation results of floor and energy absorption results of each component

5 結論及展望

1) 本文提出了一種相較于六邊形、正方形蜂窩吸能能力更加優秀的新型夾心八邊形蜂窩。首先建立了可快速預測其軸向壓縮平臺應力的理論模型并進行了尺寸參數對平臺應力及相對密度的影響分析。在八邊形蜂窩邊長確定的前提下，隨著四邊形蜂窩邊長的增加，夾心八邊形蜂窩的相對密度降低，軸向承載平臺應力逐漸減小；當四邊形蜂窩與八邊形蜂窩邊長比值固定不變時，八邊形邊長與相對密度成反比，八邊形邊長的三次方與平臺應力成反比，隨著八邊形邊長的增加，相對密度以及平臺應力都會有所降低。

2) 通過六邊形蜂窩軸向壓縮試驗和仿真對比，驗證了蜂窩建模和仿真方法的正確性；在此基礎之上，建立了新型夾心八邊形蜂窩的軸向壓縮仿真模型，對其變形模式和尺寸參數對能量吸收能力的影響進行了仿真分析，驗證了理論模型的正確性。與六邊形、正方形蜂窩吸能能力的對比分析結果表明:在保證壁厚邊長一致的前提下，夾心八邊形蜂窩的平臺應力、體積和質量比吸能3個指標均優于六邊形及正方形蜂窩，在保證相對密度一致的前提下，夾心八邊形蜂窩的3個指標均與六邊形蜂窩持平，并且大幅度優于正方形蜂窩。

3) 進行了夾心八邊形蜂窩與直升機駕駛艙簡化模型的耦合跌落仿真，定性分析了夾心八邊形與六邊形蜂窩的吸能效果。結果表明夾心八邊形蜂窩具有更高的能量吸收能力，更適用于直升機底艙耐墜性設計等對吸能能力要求較高的應用場景，今后將進一步設計完善其制作工藝。