適用于工程數據的飛行器氣動特性修正框架

李金晟，莊凌，宋加洪，盧寶剛，蘇偉，吳喬

北京航天長征飛行器研究所，北京 100076

氣動特性預示是飛行器設計、發展及鑒定的重要組成部分，預示的精準度直接影響飛行器的控制效果和仿真可信度。飛行器氣動特性預示的主要內容是建立氣動模型并量化模型不確定度，預示的技術水平取決于理論計算、風洞試驗和氣動辨識3種技術途徑的綜合運用。但由于多數飛行器飛行試驗缺乏有效激勵且傳感器測量精度較低，致使試驗數據難以滿足氣動辨識的需求，故當前工程上主要采用前兩種手段計算氣動特性。獲取的氣動特性通常由地面氣動數據表及先驗不確定性模型進行表征，前者用來預測任意飛行狀態下的氣動系數，后者用于評估預測系數的可信區間。這種預示方式存在的主要問題是：地面氣動數據表存在眾多誤差源，致使不確定性模型過于保守、給出的氣動誤差帶安全余量較大。

近年來隨著飛行試驗數據的積累，如何利用多條試驗數據進行氣動特性修正，提高氣動特性預示精準度，滿足新型飛行器精細化設計需求，成為當前工程應用領域一大難題。基于地面氣動數據表與不確定模型之間的相互依賴關系，可將該問題分解為兩個子問題:如何修正地面氣動數據表及如何量化修正后氣動模型的不確定度。

針對第1個子問題，研究人員已做了大量的工作。文獻[3]從模型驗證角度提出了一種通用思路，即基于試驗數據與預測數據之間的殘差確定一個修正項，利用其來補償原模型。修正項的表征可采用統計概率或模型擬合兩種方法，后者構建的補償差量模型具有更廣的適用范圍，故在氣動特性修正領域得到了廣泛應用。差量模型的確定本質是一個模型辨識問題，其目前主要有兩種解決思路，一是側重于建模的精度，獲得的模型結構復雜、模型項物理意義不明確，如多元單純形B-樣條法；二是側重于建模的速度，獲得的模型結構緊湊、易于使用，如逐步回歸法及多元正交函數法(Multivariate Orthogonal Functions，MOF)。考慮到氣動差量模型主要反映的是氣動特性的天地差異性，其規律相比于飛行器的完整氣動特性較為簡單，故多采用第2種思路構建模型。其中MOF由于可解決參數共線性的影響，因此應用更為廣泛。在傳統MOF的基礎上，文獻[9]將樣條因子引入模型優選程序，進一步提高了模型的非線性擬合能力；文獻[10]為構建一個適用于全局的氣動模型，引入頻數準則對多條試驗數據的氣動模型項進行了統計分析。該方法提供了一種處理多條試驗數據的思路，但其僅依賴模型項的頻數作為準入標準，優選出的模型精度依賴于飛行試驗數據的有效信息量。當信息量不足時，構建的模型不僅復雜，而且通用性不強。此外，MOF本質上基于最小二乘準則進行參數估計，因此要求組成回歸因子的解釋變量不包含任意誤差，從而難以應用于測量精度不高的試驗數據。綜上所述，目前對于如何基于多條有效信息不足且測量精度不高的試驗數據進行氣動差量模型的辨識，并沒有一種很好的解決方案。

針對第2個子問題，即完成對地面氣動數據表的修正后，如何進一步量化氣動修正模型的不確定性，目前鮮有研究。文獻[11]在辨識差量模型的基礎上，提出一種利用預測區間量化模型不確定度的方法，其基于概率的思想，能給出具有不同置信水平的不確定性區間。這種不確定性量化方法的預測效果依賴于訓練集中試驗數據的包絡范圍，當待估計狀態位于有效包絡范圍內時，預測的誤差帶較為精準；反之，給出的誤差帶范圍過大，無法滿足精細化設計的需求。

本文主要貢獻是提出一種適用于多條飛行試驗數據的氣動特性修正框架，實現了對地面氣動模型及先驗不確定性模型的修正。具體針對差量模型的辨識，首先為解決試驗數據有效信息不足問題，一方面引入迭代思想改進了多元正交函數法，另一方面基于模型項的頻數及可信度，構建了兩個統計優選準則；然后為解決試驗數據精度不高的問題，基于總體最小二乘思想，設計了適用于氣動參數估計的定制化算法。針對模型的不確定度量化，首先基于不確定性理論，估計出氣動修正模型的總偏差；最后基于貝葉斯估計準則，將地面的先驗不確定性信息與估計的飛行不確定性信息進行整合，構建了一個新的不確定性模型。

1 問題描述

針對所研究的飛行器，目前在進行彈道仿真評估分析時，工程上多采用地面氣動數據表及先驗不確定性模型預示氣動特性，分別給出任意狀態下的氣動系數值及其誤差帶范圍[-,]，表達式為

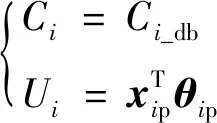
(1)

式中：_db為基于地面氣動數據表插值所得的六分量氣動系數；p為回歸因子向量；p為先驗參數，其值通常基于經驗確定。

由于成本及試驗條件限制，可直接獲得的飛行試驗數據主要有兩類：一是彈載慣性測量系統(IMU)測量的視加速度及角速度；二是地面雷達測量的位置及速度。基于試驗數據，結合實測的大氣數據，完成彈道參數重建及氣動系數換算，是進行氣動辨識修正的前提。目前基于飛行后試驗數據進行彈道重建的方法已較為成熟，根據是否考慮測量噪聲的影響，分為隨機性濾波平滑法和決定性輸出誤差法。本文基于文獻[13]構建的飛行器動力學及運動學方程，應用文獻[14]提出的濾波平滑框架(將擴展卡爾曼濾波與Fraser-Potter平滑器進行結合)，以IMU測量數據作為輸入數據、雷達測量數據作為觀測數據，完成彈道重建，獲得未直接測量的狀態參數。然后計算氣動系數的測量值_mea：

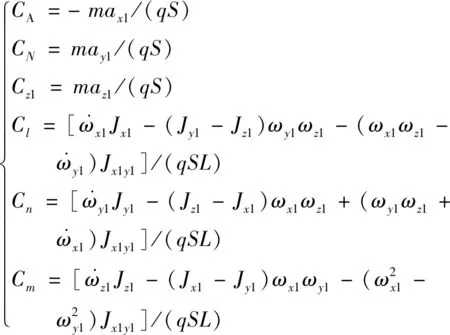
(2)

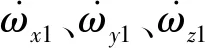
重建后獲得的完整彈道數據，本文稱之為低質量數據，其具有如下特點：試驗缺乏主動激勵，數據有效信息不足；飛行試驗狀態不同，數據相似性較低；傳感器測量及彈道重建方法都存在誤差，數據精度不高。本文研究目的就是基于多條低質量試驗數據，完成對_db及的修正，從而提高氣動特性的預示精準度。基于該目的，最終構建的氣動特性修正框架如圖1所示。

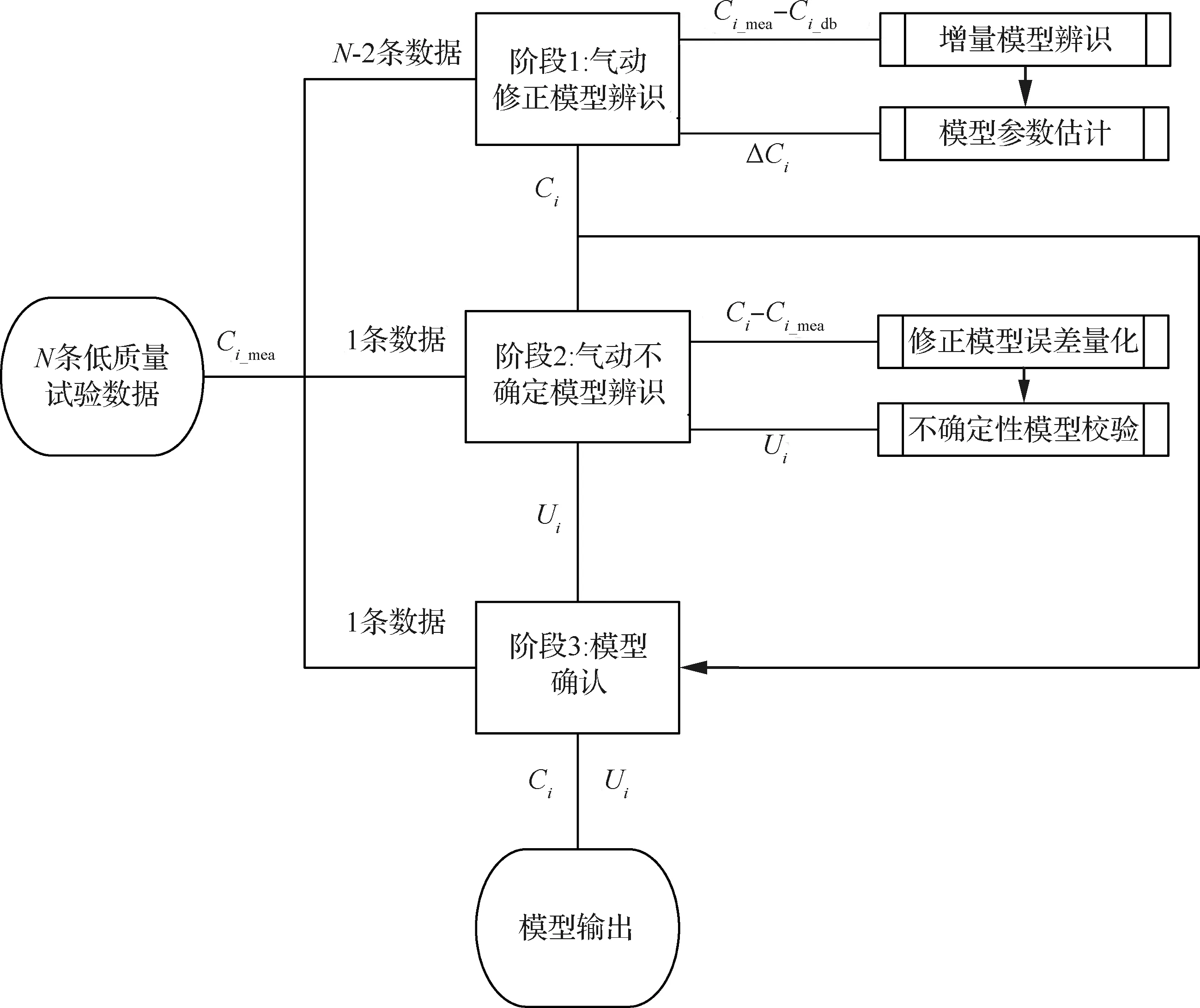
圖1 氣動特性修正框架Fig.1 Aerodynamic characteristic correction framework

2 氣動差量模型辨識

地面氣動模型修正的基本思路是：基于_mea與_db之間的殘差_db，構建一個能夠反映氣動特性天地差異性的補償差量Δ，并以此構建氣動修正模型，表達式為

=_db+Δ

(3)

基于定常流動假設，Δ如下參量有關：

Δ=(,,,,,,,)

(4)

式中：為飛行馬赫數；為攻角；為側滑角；、及為等效控制舵偏角，分別對應俯仰、偏航及滾轉；為飛行高度；為角速度，主要影響力矩系數。

由式(3)可得，氣動模型修正的關鍵在于差量模型的辨識。為此本文提出一種針對低質量試驗數據的氣動模型混合辨識思路：首先引入迭代思想改進多元正交函數法，基于每一條試驗數據完成差量模型的辨識；然后設計一種新的模型項優選準則，實現對多個氣動模型的統計優選；最后采用總體最小二乘思想，解決參數的混合估計問題。

2.1 模型辨識方法

針對任意線性模型：

=+

(5)

式中：∈×1為響應向量，為觀測樣本點數；∈×1為與響應向量對應的觀測噪聲向量；∈×為解釋矩陣，元素(=1,2,…,) 為回歸因子，可由解釋變量及其組合項組成，其通常為多項式，但為增強模型的局部建模能力，也可引入樣條函數；∈×1為未知參數向量，可基于最小二乘法(Least Square，LS)進行估計，結果為

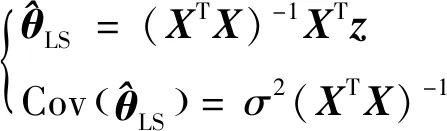
(6)

式中：為測量噪聲方差，如果未知則可由殘差進行估計：

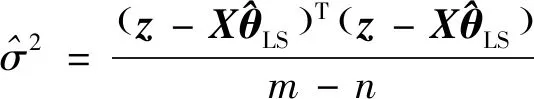
(7)

多元正交函數法是一種基于最小二乘準則的模型結構優選方法，其應用流程歸納如下：

1) 生成正交回歸因子。應用Gram-Schmidt程序處理原始回歸因子，獲得正交回歸因子，表達式為

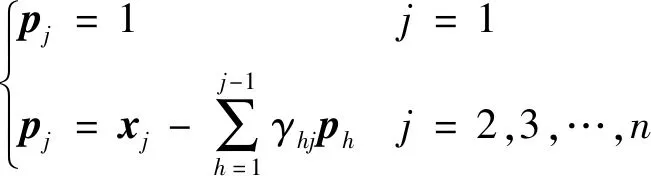
(8)

=

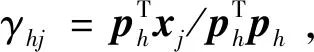
(9)

2) 正交模型參數估計。將代入式(5)，產生新的回歸模型，其中為對應于正交回歸因子的參數向量。由于正交化后，為對角矩陣，故正規方程可以解耦，式(6)可簡化為

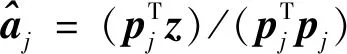
(10)

3) 正交模型結構確定。正交回歸因子模型項的具體選擇以最小化預測平方誤差(Predicted Squared Error，PSE)準則為基準，其由平均平方誤差項(Mean Squared Fit Error，MSFE)及過擬合懲罰項(Overfit Penalty，OFP)組成：

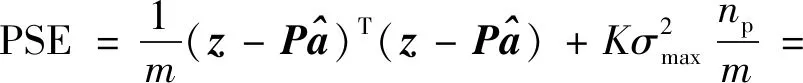
MSFE+OFP

(11)

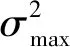
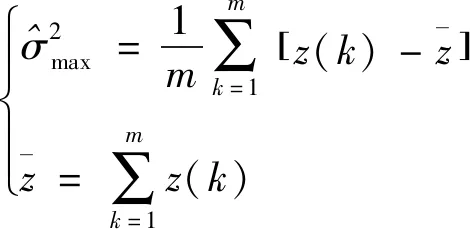
(12)

為進行回歸因子的優選，需首先量化回歸因子模型項的顯著性。傳統的MOF法定義回歸因子減小MSFE能力作為顯著性評估指標，經過推導可得，每一個正交回歸因子的能力表示為

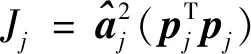
(13)

基于大小，按照由大到小的順序引入回歸因子。由于MSFE和OFP分別單調遞減、遞增，故PSE必然有一個全局最小值，從而可優選出具有個回歸因子的模型結構，其兼顧了擬合能力和泛化能力。

4) 正交模型轉化為原始模型。基于式(9)，可將優選出的正交回歸模型分解為具有物理意義的原始回歸模型。由式(8)和式(13)可得，基于顯著性大小引入正交回歸因子的次序，直接影響了原始回歸因子的個數，當某一靠后的正交回歸因子具有較大的顯著性時，其分解后將產生較多原始回歸因子，從而使得優選出的原始模型不緊湊，難以應用于低質量的飛行試驗數據。為此本文基于模型吝嗇建模準則，提出迭代優化思路。

5)迭代優選回歸因子。首先調節的大小，確定正交回歸因子的期望個數；然后基于正交回歸因子的顯著性次序，調節原始回歸因子的次序，重新進行步驟1)～4)；繼續迭代，直至正交回歸因子與原始回歸因子的數目接近。

基于迭代思想改進的多元正交函數法，可辨識出更為緊湊的模型結構。但由于試驗數據有效信息不足，致使針對一條數據確定的氣動差量模型，無法實現對地面氣動特性全面、精準的補償。解決這一問題的直接手段是統計分析，關鍵在于統計準則的構建。本文采用統計量表征模型項的可信度，然后結合模型項的頻數，構建了兩個統計準則，具體為

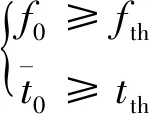
(14)

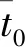
2.2 參數估計方法

經由統計分析獲得氣動差量模型后，接下來的重點就是基于多條試驗數據，估計氣動模型參數。目前主要有兩種方式解決氣動參數的混合估計問題，分別是基于最小二乘準則的一次性方法及基于貝葉斯準則的迭代方法。當沒有參數的先驗信息時，第一種方式更為簡單實用。但是LS本質上要求回歸變量不包含測量噪聲，難以應用于低質量飛行試驗數據。為此研究人員引入總體最小二乘法(Total Least Square，TLS)進行氣動參數估計，當回歸因子測量誤差不可忽略時，TLS比LS具有更高的估計精度。

總體最小二乘法主要用來處理誤差變量模型(Error-In-Variables，EIV)，即同時考慮回歸因子與響應變量誤差的線性模型，其形式為

=(-)+

(15)

總體最小二乘問題的優化準則為

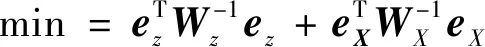
(16)

式中：∈×、∈×為相應噪聲協方差矩陣；∈×1=vec(), vec(·)表示矩陣的拉直運算，其將矩陣按列重新排列成一個新的列向量。

總體最小二乘問題的求解方法取決于噪聲矩陣的形式，噪聲信息越多，參數估計精度越高，但計算過程也越復雜。具體應用于氣動參數估計時，主要存在兩個難點: ① 模型中部分回歸因子，如常數項，是精確已知的，無法直接基于TLS思想進行處理; ② 回歸因子和響應變量的噪聲方差特性不同，不滿足經典TLS方法的應用前提。

針對難點 ①，本文應用混合LS-TLS問題構型進行求解，即基于QR分解將數據矩陣進行分割，將混合問題轉化為最小二乘估計和總體最小二乘估計兩個子問題：

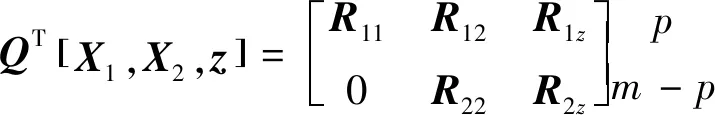
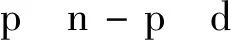
(17)

式中：∈×是由精確已知的回歸因子組成的解釋矩陣；∈×(-)中的回歸因子包含測量誤差；由于本文主要針對單響應變量，故=1；待估計參數=[,]可分別基于LS和TLS思想求解獲得：

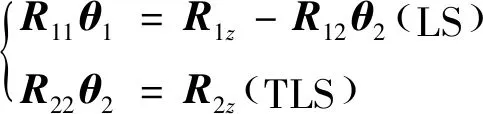
(18)

針對難點 ②，基于低質量數據特點，忽略噪聲的自相關性及互相關性，即假設為對角矩陣且元素相等、=diag(,,…,)且∈(-)×(-)為對角矩陣；簡化后采用廣義總體最小二乘法求解，具體有兩種計算手段，即數據縮放和廣義的奇異值分解。數據縮放處理過程較為簡便，其核心思想是基于權重特性=diag(,)將復合數據矩陣=[2]進行歸一化，表達式為

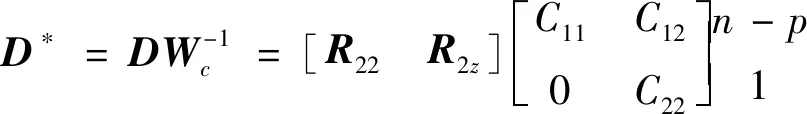
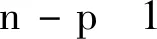
(19)

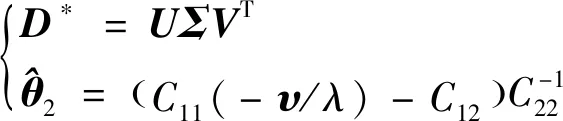
(20)

式中：∈(-)×(-+1)為奇異值矩陣；、分別為左、右奇異矩陣；、分別是最后一列的最后一個元素、前-個元素。

完成對的估計后，代入式(18)，應用LS便可實現對的估計，參數估計的協方差可由式(21) 進行統一計算：

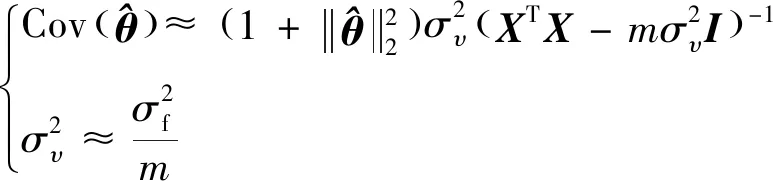
(21)

式中：為最小的奇異值。

3 不確定性模型修正

基于差量模型完成對地面氣動系數的修正后，需重新量化修正模型的誤差范圍。本文在地面先驗不確定性模型的基礎上，提出了一種新的不確定度量化思路：首先基于不確定性理論，計算修正氣動系數的總偏差；然后基于貝葉斯估計準則，應用氣動總偏差校正先驗不確定性模型。

3.1 不確定度量化

氣動修正模型的總偏差Δ主要包括兩部分： ① 測量氣動系數與修正氣動系數的殘差_； ② 測量氣動系數的測量誤差_mea，表達式為

Δ=|_c|+|_mea|

(22)

式中：_=_mea-(_db+Δ)；、為權重。

由于_mea是通過彈道重建獲得而非直接測量，因此其測量誤差可通過對重建過程進行不確定性分析計算。不確定性分析是研究重建參數可信度的一種常用手段，其通過研究重建過程的輸入誤差、模型誤差及重建方法誤差的傳遞影響，來量化重建輸出參數的不確定性分布。對于彈道重建來說，當選定重建模型及方法后，重建過程的主要不確定性便是輸入不確定性。輸入不確定性又可分為隨機不確定性和認知不確定性，本文分別采用概率法及區間分析法進行建模，具體特性如表1所示。

提取出不確定性因素后，接下來為量化輸出的統計分布，需進行不確定性傳遞分析。不確定性傳遞主要以輸出為對象，量化不確定性輸入經過系統傳遞對輸出的影響，具體傳遞方法的選擇取決于不確定性輸入的類型。由表1可得，彈道重建輸入同時包含隨機和認知不確定性，其屬于混合不確定性傳遞問題。對于這種情況，目前應用最為廣泛的是雙層蒙特卡洛法，其基本思想是：認知不確定性參數在外層蒙特卡洛模擬中采樣，隨機不確定性參數在內層蒙特卡洛模擬中采樣，統計結果由p-box圖呈現。但對于彈道重建，如果直接應用雙層蒙特卡洛法，需存儲所有的打靶數據，并且需要對每一時間點的彈道參數進行手工處理以獲得p-box圖，處理程序較為繁瑣。為此本文對雙層蒙特卡洛法進行了簡化，基于遞推方式直接計算每一時間點處各彈道參數的均值和方差，具體步驟如下：

表1 彈道重建輸入不確定性特性Table 1 Characteristics of input uncertainty in trajectory reconstruction

根據不確定性變量的模型，采樣生成個樣本點{a_,e_}1≤≤。其中和分別是隨機不確定性向量和認知不確定性向量。假設服從高斯分布，由于是區間形式，沒有概率意義，故假設服從均勻分布。然后統一采用隨機采樣法獲得樣本點。

基于彈道重建算法，計算每一個樣本點的系統響應值(輸出參數及六分量氣動系數)的時間歷程，{=[(),…,()]}1≤≤。

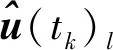
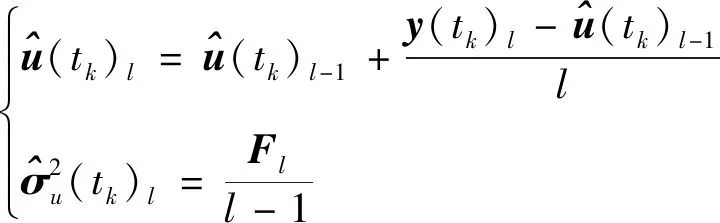
(23)

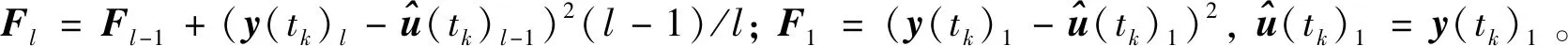
3.2 模型混合估計

氣動修正模型的總偏差Δ側重于表征由氣動辨識引入的誤差，稱之為飛行不確定性；地面先驗不確定性模型則側重于表征由風洞試驗及氣動系數工程計算方式等引入的誤差，稱之為地面不確定性。為更精準地反映氣動修正模型的誤差特性，需同時考慮上述兩類誤差的影響。為此本文基于貝葉斯準則，利用Δ來校驗地面不確定性模型的參數，其代價函數為

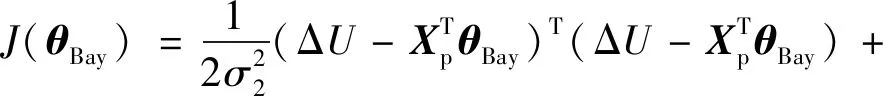
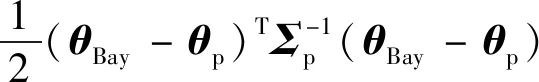
(24)

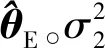
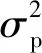
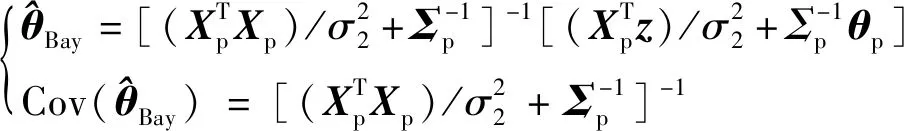
(25)

4 試驗數據結果分析

某型飛行器迄今已積累了10條飛行試驗數據，經由數據預處理及彈道重建后，可獲得氣動辨識所需的完整彈道參數及氣動系數的時間歷程。本文應用所提出的氣動特性修正框架(圖1)對重建數據進行處理，具體給出軸向力系數、法向力系數及俯仰力矩系數的修正結果。

4.1 氣動修正模型

考慮到該型飛行器的飛行特點(速度快、空域廣且飛行狀態變化明顯)及重建數據的低質量特性，難以直接辨識出一個適用于全局的氣動差量模型。為此本文采用數據分割思想，選擇飛行高度、攻角及側滑角作為分割變量，將飛行包絡分為4個區間，即高空小攻角小側滑、高空大攻角小側滑、中空小攻角大側滑及低空大攻角大側滑；然后分別在每一個區間內進行辨識，確定出局部差量模型；最后基于線性加權思想融合不同局部模型，實現模型在區間交界處的平滑過渡。

低空大攻角大側滑段主要進行速度控制，機動程度高、氣動特性差異顯著，故本文重點針對該區間進行分析。選擇一條飛行試驗數據Y1，其在低空大攻角大側滑段內的大氣風場測量結果如圖2 所示，高度、馬赫數、攻角及側滑角的重建結果如圖3所示。

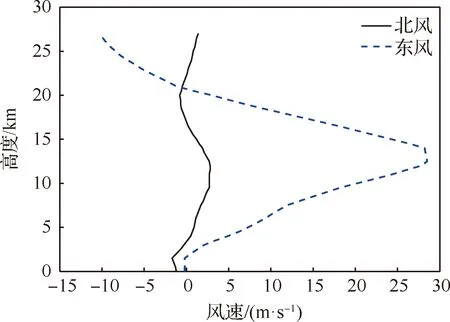
圖2 風場測量結果Fig.2 Wind field measurement results

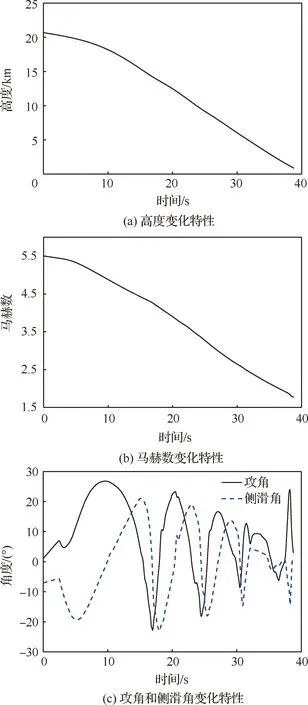
圖3 彈道參數重建結果Fig.3 Trajectory parameters reconstruction results

隨機選擇8條試驗數據作為訓練集，進行氣動差量模型的混合辨識。首先針對每一條試驗數據，采用改進的多元正交函數法進行模型結構辨識，候選集中的模型項最高階數設計為2；然后基于頻數及可信度準則對辨識所得的8個模型進行統計優選。具體對于軸向力系數，應用迭代多元正交函數法處理Y1試驗數據的結果如表2所示，對8個差量模型的統計優選過程如圖4所示。

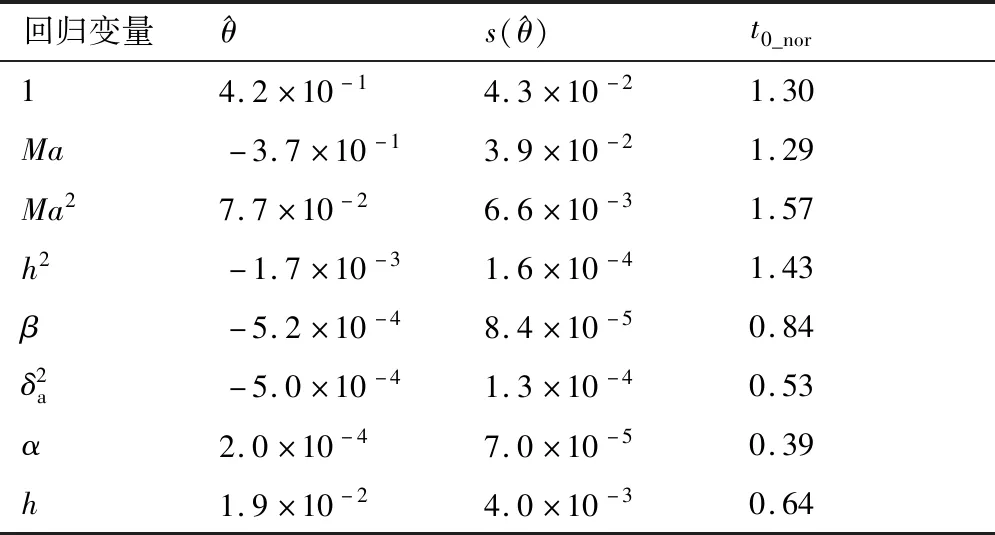
表2 單數據差量模型辨識結果Table 2 Single data difference model identification results

圖4 差量模型統計優選結果Fig.4 Statistical optimization results of difference model

基于選定的Y1數據進行差量模型辨識時，設計=40，采用傳統MOF計算，產生8個正交回歸因子、15個原始回歸因子；基于迭代的MOF，最終產生7個正交回歸因子、8個原始回歸因子，見表2。考慮到模型結構辨識的高實時性要求，采用LS方法快速估計參數，確定模型項的值。此外為降低試驗數據的不同狀態對模型項可信度的影響，本文將值進行了歸一化處理。

進行統計優選時，本文設計頻數閾值=4，可信度閾值=087，是訓練集中試驗數據數目的一半，是所有模型項可信度的均值。由圖3可得，影響Δ的回歸因子數目眾多，且其頻數及可信度差異較大。這是因為飛行試驗缺乏有效激勵，使得每一條試驗數據只能反映出部分修正特性。如果試驗數據中所有出現的影響項都作為Δ的回歸因子，則會導致模型結構復雜，不便于使用且容易造成過擬合。因此本文重點關注訓練集所反映出的主要氣動特性修正規律，即確定具有普適性且可信度較高的回歸因子。完成模型結構的構建后，應用總體最小二乘思想估計模型參數，獲得3個氣動系數的差量模型(式(26))，然后將其代入式(3)可得氣動修正模型。

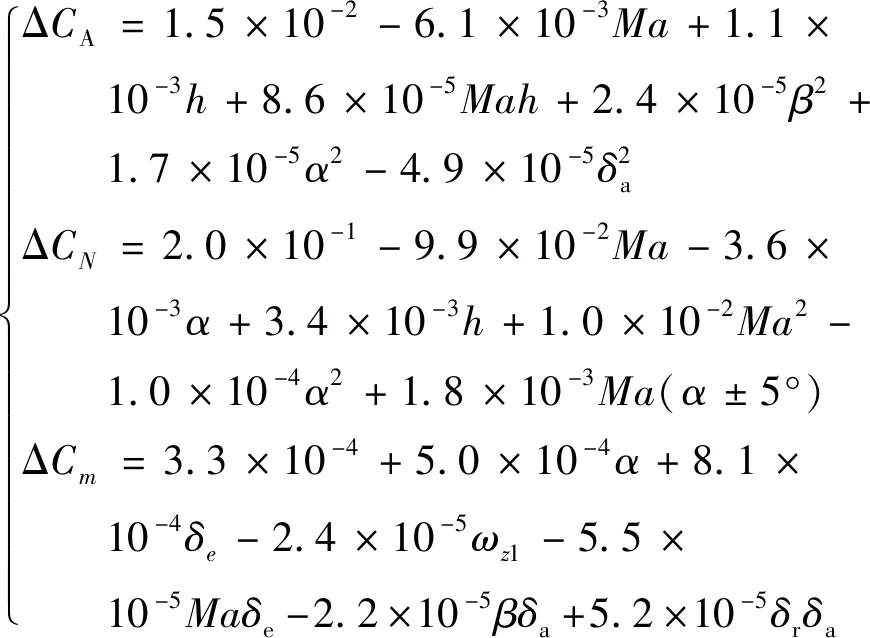
(26)

式中：(±5°)是樣條回歸因子，基本定義為

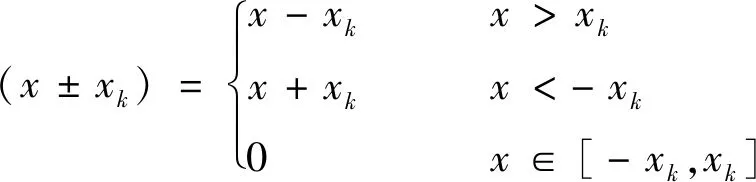
(27)

其中：是對應于回歸因子的樣條節點。考慮到飛行器的機動特性，本文只針對攻角和側滑角，分別設計了兩個節點，即5°和10°，然后將其作為候選模型項。

首先從氣動設計角度，分析差量模型的物理意義。對于低空大攻角大側滑段，基于地面氣動數據表預示的氣動系數主要有兩方面的誤差。一是氣動系數的提供方法，其在工程中基于廣義氣動力近似公式計算，忽略了三通道的耦合性。該誤差主要影響氣動力矩系數，體現在差量模型中的和δ項；二是風洞試驗數據的準度，主要考慮馬赫數、雷諾數模擬不完全形成的天地差異和飛行器外形變化引起的氣動系數偏差。前者體現在差量模型中的及相關因子，主要影響力系數；后者雖然對3個氣動系數都有顯著影響，但難以從理論上確定直接的關聯量。考慮到差量模型中的剩余回歸因子，如、、、和，都是相應系數的主要影響量，故將其作為外形變化引起的氣動特性補償量具有一定的合理性。

接著從模型擬合角度，分析差量模型的規律特性。在給定區間，氣動差量模型對訓練集數據測量殘差的擬合效果見圖5。差量模型的擬合精度采用均方根誤差(Root Mean Squared Error，RMSE)進行衡量。Δ、Δ及Δ的RMSE分別是0.010 9，0.046 0和0.001 7。其中對于Δ，如果將樣條項(±5°)替換為，則擬合誤差增加到0.051 1，說明樣條項能在一定程度上改善局部建模精度。由于差量模型的本質是表征一個共性的修正規律，故其擬合精度主要取決于所有試驗數據的殘差特性。具體來說，俯仰力矩系數的殘差規律較為一致，優化出的Δ擬合精度最高，估計的補償值整體上圍繞0值波動；法向力系數殘差的差異性最為顯著，故Δ的擬合精度相對最低，其補償值同樣在0值附近波動；對于軸向力系數，多數試驗數據具有正的殘差特性，故Δ反映出一種接近常值的補償特性，但由于數據6和7的存在，導致擬合精度不高。

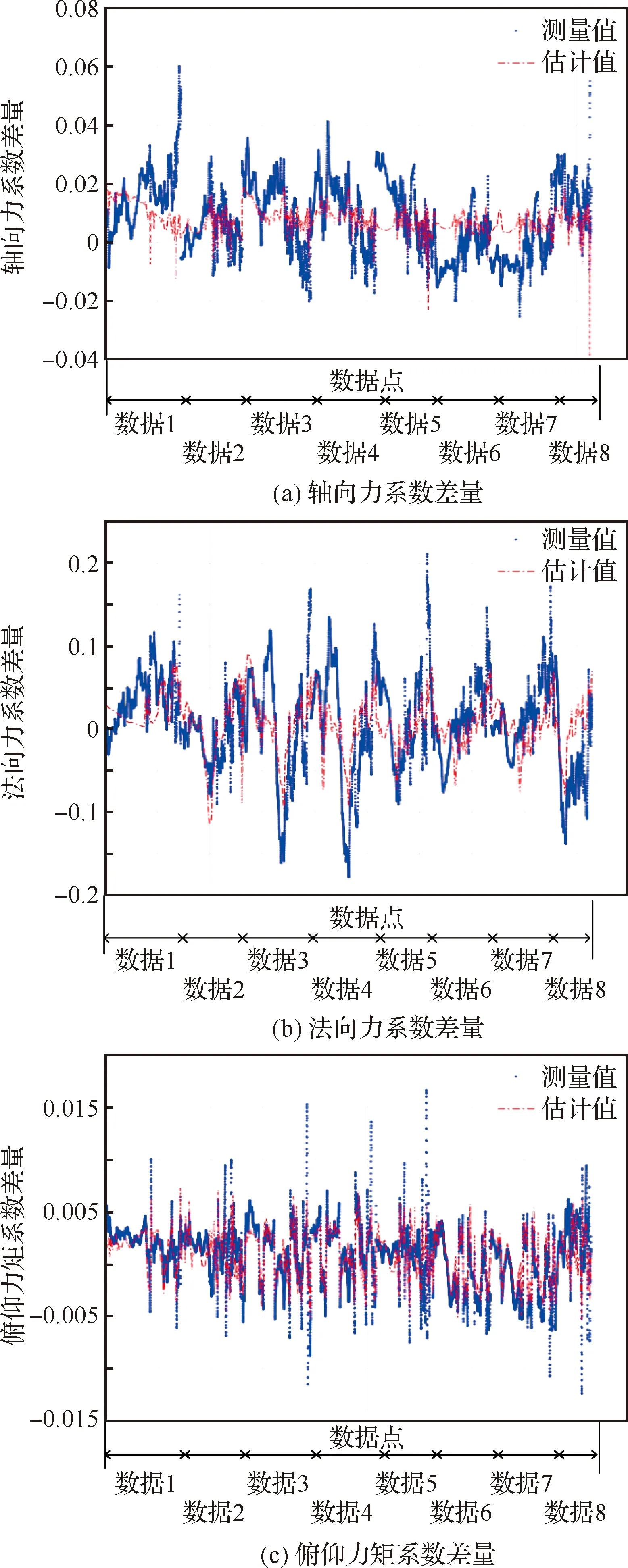
圖5 差量模型在訓練集的擬合效果Fig.5 Fitting effect of difference model in training set

4.2 氣動不確定性模型

基于辨識所得的氣動修正模型，再引入1條試驗數據，校驗地面先驗氣動不確定性模型。首先基于不確定性分析理論量化3個修正模型的總偏差Δ、Δ及Δ，相關結果如圖6所示。

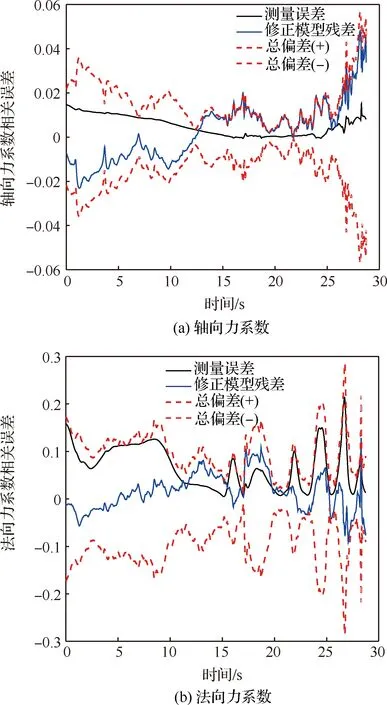
圖6 修正氣動模型的總偏差Fig.6 Total deviation of corrected aerodynamic model

基于確定出的Δ，應用模型混合估計方法校正先驗氣動不確定性模型，相關結果如表3所示。先驗不確定性模型，是由設計人員基于氣動系數的特性及工程經驗進行定制化設計而得，不同的模型包含不同的回歸因子，模型結構較為簡單。大量試驗表明，僅改變原模型參數，難以提高不確定性模型的精準度。為此首先對已有的先驗回歸因子進行整合，然后又引入了兩個新的變量及，最終構建一個通用的不確定性模型結構。

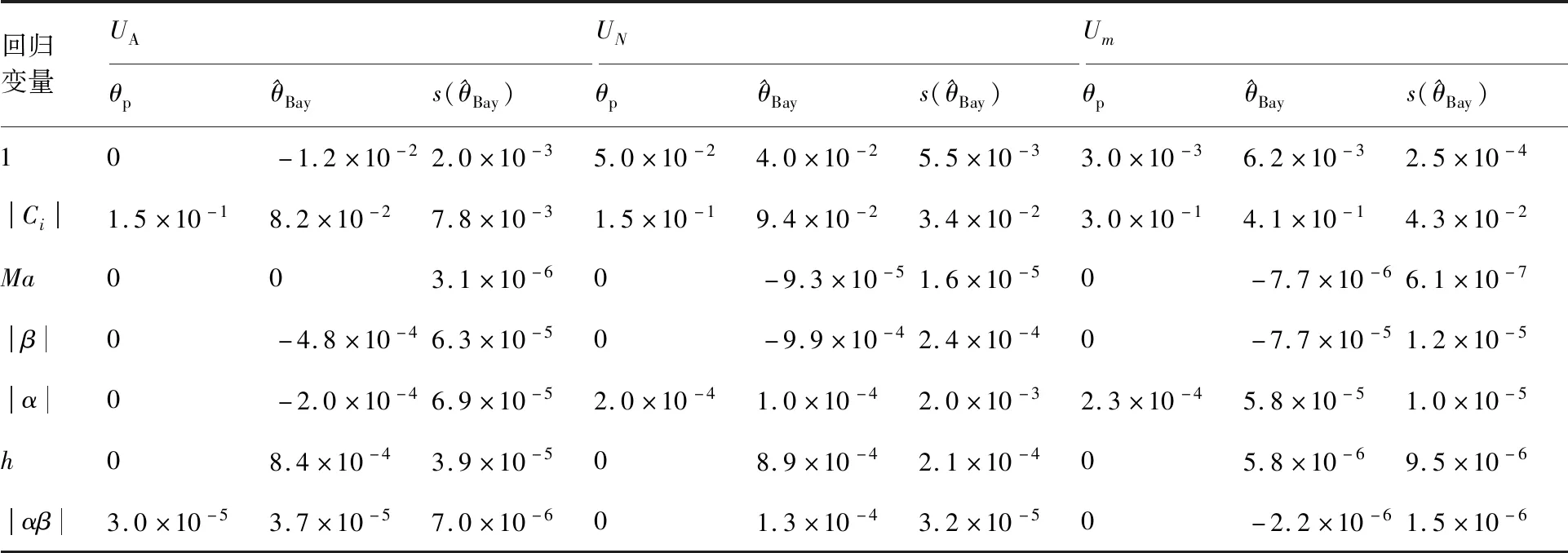
表3 不確定性模型修正結果Table 3 Correction results of uncertainty model

對于俯仰力矩系數，本文給出不確定性模型修正前后的對比結果。圖7(a)給出的是先驗不確定性模型確定的誤差帶范圍對原殘差_db的包絡特性，可見誤差帶整體安全余量較大、局部余量不足，即精細度不滿足要求、可靠性仍有不足；圖7(b)反映的是先驗誤差帶對修正模型殘差_的包絡情況，經過氣動差量模型的補償后，不再有超出誤差帶的測量點，即提高了可靠性，但誤差范圍仍較為寬泛；圖7(c)給出了氣動模型及不確定模型的綜合修正結果，其在保持高可靠性的基礎上，前15 s的誤差帶范圍有顯著縮小，即進一步提升了精細程度。

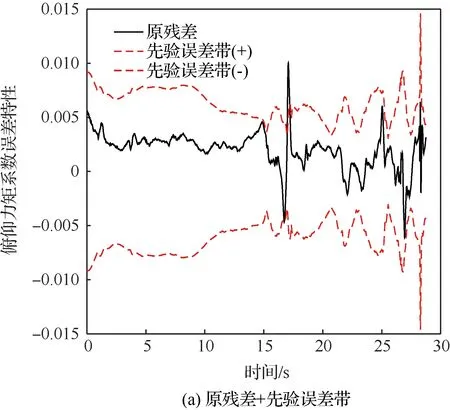
圖7 氣動誤差帶對比分析Fig.7 Comparative analysis of aerodynamic error band

4.3 模型確認

最后基于1條未使用的試驗數據，進行氣動修正模型及氣動不確定性模型的確認。具體針對每一個氣動系數，首先給出3種方式計算所得的氣動系數值，分別是基于地面氣動數據表的插值方法、基于試驗測量數據的換算方法及基于修正模型的預示方法；然后對模型修正效果進行對比分析，分別給出“地面氣動數據表+先驗不確定性模型(方式1)”“氣動修正模型+先驗不確定性模型(方式2)” “氣動修正模型+修正不確定性模型(方式3)”的預測特性，相關結果如圖8～圖10所示。

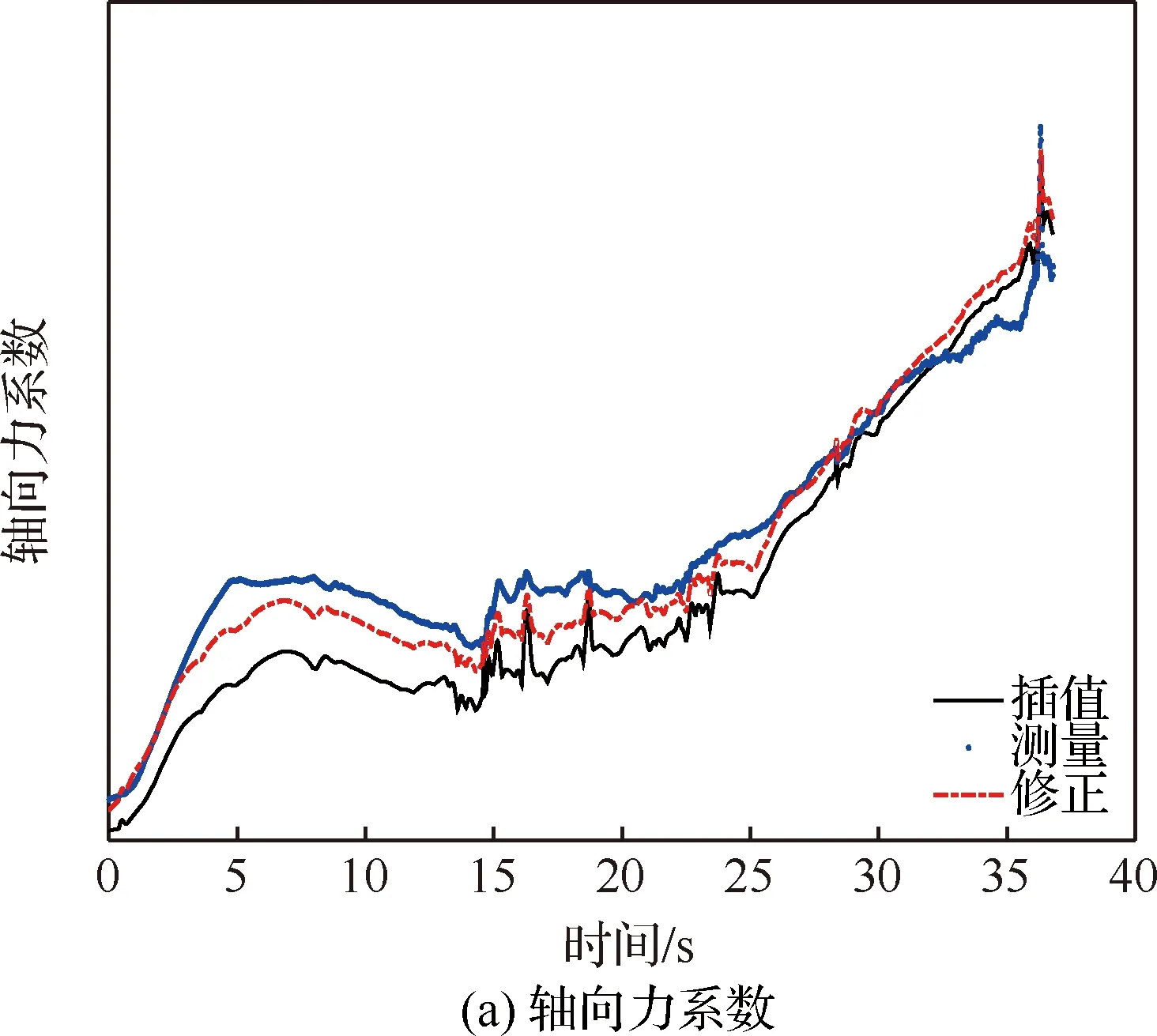
圖8 氣動系數預測值Fig.8 Prediction value of aerodynamic coefficients

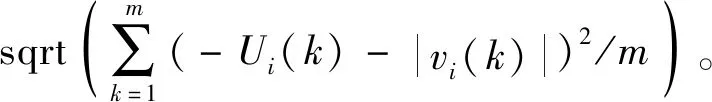
由圖8～圖10和表4可得，經過差量模型的補償修正后，測量殘差具有不同程度的減小，說明氣動修正模型可改善氣動系數的預示精度；“氣動修正模型+先驗不確定性模型”預示方式具有最少的誤差帶外測量點數，即氣動修正模型也可提高氣動預示的可靠性；氣動系數經由差量模型修正后，采用修正不確定性模型確定的氣動誤差帶，具有最小的剩余安全裕度，反映出修正不確定性模型的高精細度。綜合來看，“氣動修正模型+修正不確定性模型”預示方式相比于“地面氣動數據表+先驗不確定性模型”方式，可以有效提升氣動特性預示的精準度，從而能夠滿足新型飛行器精細化氣動設計的需求。

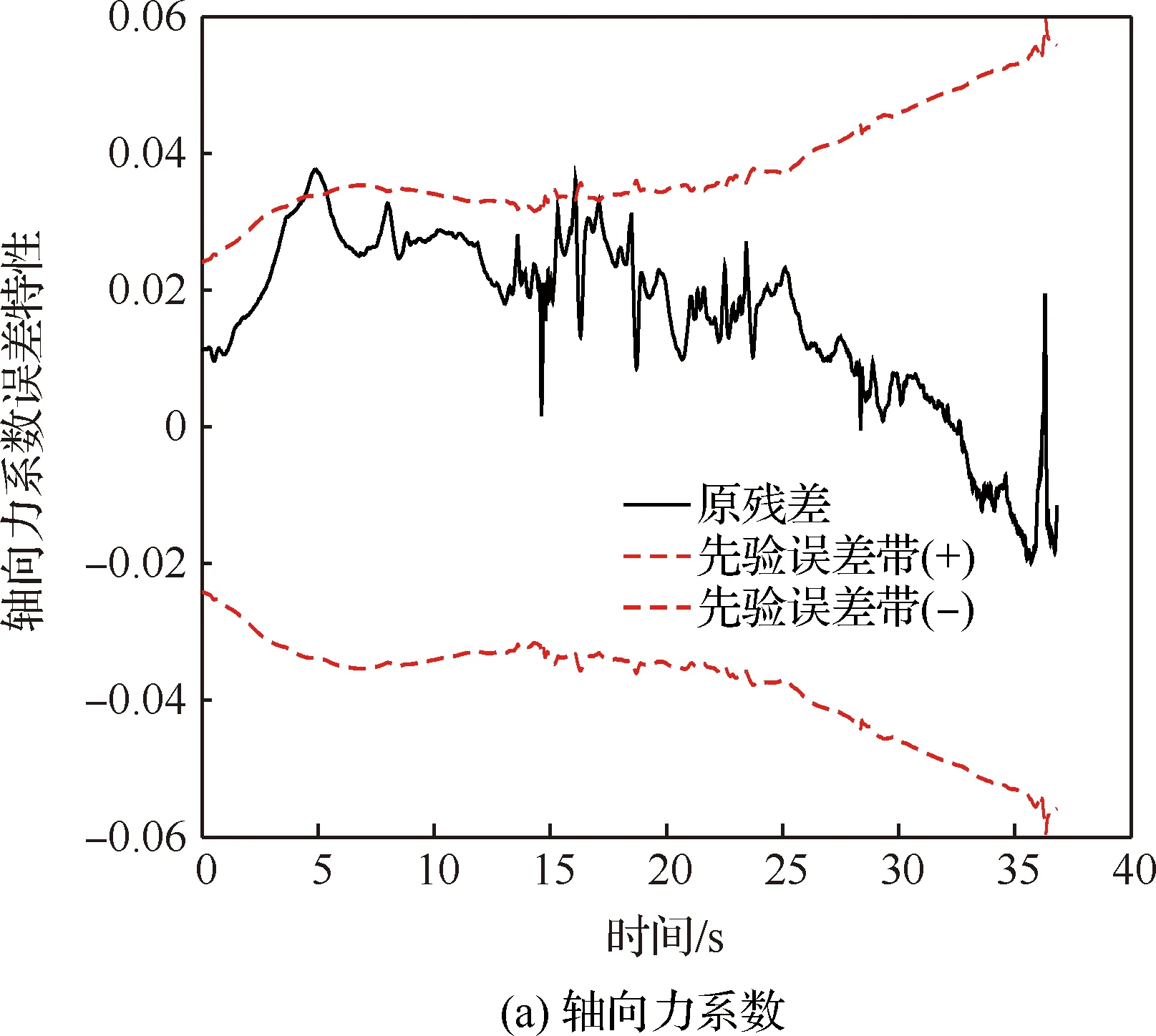
圖9 原殘差+先驗誤差帶Fig.9 Original residual+prior error band

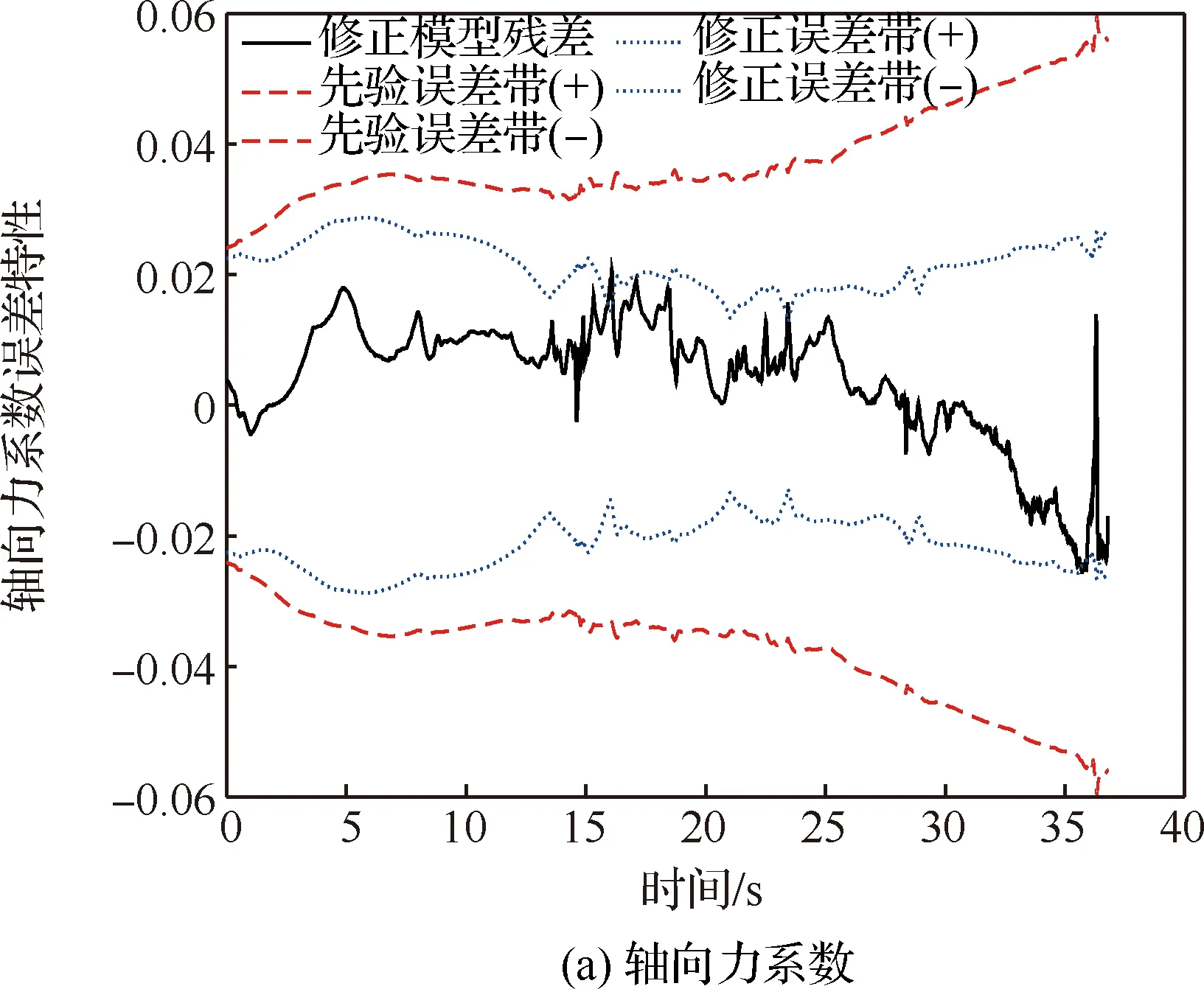
圖10 修正前后誤差帶對比Fig.10 Comparison of error bands before and after correction

表4 不同氣動特性預示方式對比結果Table 4 Comparison results of different aerodynamic characteristic prediction methods

5 結 論

本文提出一種適用于多條低質量飛行試驗數據的氣動特性修正框架。針對某型飛行器，重點在低空大攻角大側滑段對地面氣動預示特性進行了修正，具體結論如下：

1) 相比于地面氣動數據表，氣動修正模型預測的氣動系數更接近測量的氣動系數，即差量模型能夠補償一定的地面預示誤差，提高氣動系數的預示精度。

2) 氣動修正模型結合先驗不確定性模型具有最高的預測可靠性，確定的氣動誤差帶具有最少的誤差帶外測量點，說明差量模型的補償也能提高預示的可靠性。

3) 氣動修正模型結合修正的不確定性模型能夠給出精細度最高的氣動誤差帶，其預示可靠性雖低于“氣動修正模型+先驗不確定性模型”方式，但高于“地面氣動數據表+先驗不確定性模型”方式，從而有效地提高了氣動設計的精準度。