類X-43A飛行器高超聲速分離仿真

趙飛，劉麗玲，石泳，左光，萬千，張宇佳

1.中國空間技術研究院 錢學森空間技術實驗室，北京 100094

2.中國礦業大學(北京) 機電與信息工程學院，北京 100083

高超聲速飛行器具備高速巡航、快速突防、靈活機動的優勢，在軍事和航空航天領域廣泛應用。但高超飛行器在執行任務過程中，有時會存在多體分離或載荷釋放的過程，如助推器與巡航飛行器分離、火箭助推級與芯級分離、彈箭分離等，由于其外形日趨復雜，在高超聲速分離過程中，級間的流動干擾變得尤為突出，從而嚴重影響各級飛行器氣動力/力矩特性，進而對分離過程中飛行器姿態產生影響，甚至危及飛行安全。因此，亟需對高超聲速飛行器多體分離過程開展試驗和仿真研究。

在高超聲速多體分離試驗方面，國內外主要的空氣動力研究機構研制了大量多體分離試驗裝置，并進行了較成熟的多體分離試驗。例如，美國的AEDC風洞早在20世紀70年代便配備了六自由度捕獲軌跡系統(CTS)，具備多種飛行器串/并聯級間分離等試驗能力；法國ONERA同樣在20世紀70年代就具備了寬速域下的CTS試驗能力，并進行了大量相關試驗研究；中國的多體分離試驗起步相對較晚，主要的研究機構有中國航天空氣動力研究院和中國空氣動力研究與發展中心，進行了網格測力和CTS級間分離氣動干擾特性風洞試驗，取得了不少成果。

針對多體分離數值仿真，國內外開展了一些工作，但重點多集中于空中投放、火箭端面串聯方式的級間分離等方面，在這些研究中兩級通常為簡單的鈍頭旋成體結構，級間分離氣動干擾較小，目前先進的高超聲速飛行器為了減小氣動阻力，一般采用面對稱、細扁薄的外形，且巡航級和助推級采用尾端面和底面共同連接的形式，使級間分離干擾更加復雜，而針對此類高超飛行器的分離特性研究較少。美國X-43A飛行器為典型的扁平構型，端面和底面與助推火箭通過適配器連接，本文以類X-43A飛行器為研究對象，采用網格變形/局部網格重構的方法對其高超分離過程進行仿真模擬，重點關注連接處的分離干擾，并分析初始分離攻角、彈射力對分離過程的影響。

1 數值模擬方法

1.1 數值算法

采用三維雷諾平均Navier-Stokes方程作為控制方程，其表達式為

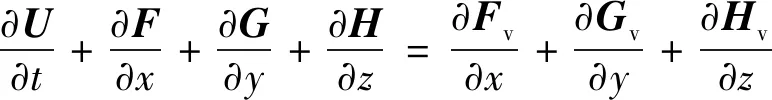
(1)

式中：為守恒變量；、、表示無黏對流通量；、、為黏性通量。

湍流模型采用-SST兩方程模型，其湍動能輸運方程和湍流比耗散率方程為

-

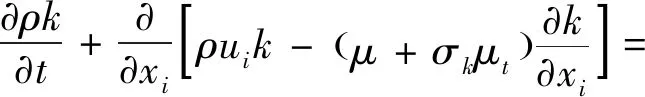
(2)

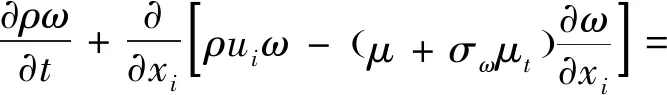
-+2(1-)

(3)

式中：和分別為方程和方程的系數；和為湍流模型系數；為湍流模型系數的合成函數。控制方程的空間離散方法采用具有較高黏性分辨率且收斂性較好的Roe-FDS格式。

1.2 飛行力學模型

本文所用飛行力學模型基于剛體的六自由度運動，具體模型方程為

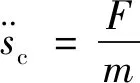
(4)

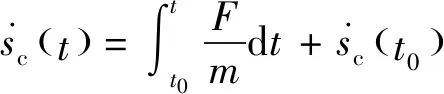
(5)

′=′′+′×(′′)

(6)

′=′

(7)

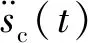
1.3 網格變形/局部重構算法

針對類X-43A分離仿真，采用網格變形與局部重構相結合的方法，在單時間步位移較小的情況下采用Laplace算法進行網格變形，使式(8)所示的二次方程最小化：

(8)

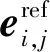
1.4 仿真模型和邊界條件

采用的分離仿真模型由類X-43A飛行器與助推火箭兩級構成，總長15 m，飛行器長3.63 m，助推器長12.55 m。類X-43A飛行器采用乘波體構型，機身下表面壓縮面作為乘波前體，該構型一方面產生高升力，同時為吸氣超燃沖壓發動機提供高品質來流。助推器采用大三角翼面，并包含三片梯形尾翼。飛行器下部和尾部端面通過適配器與助推器連接，如圖1所示。圖2展示了飛行器和級間連接處附近的網格，由于在利用網格變形/局部重構算法對分離問題進行仿真時需要各分離體之間存在明確的邊界，且邊界之間存在網格，為了使仿真能夠有效進行，初始狀態二者之間預留1 mm的間距。

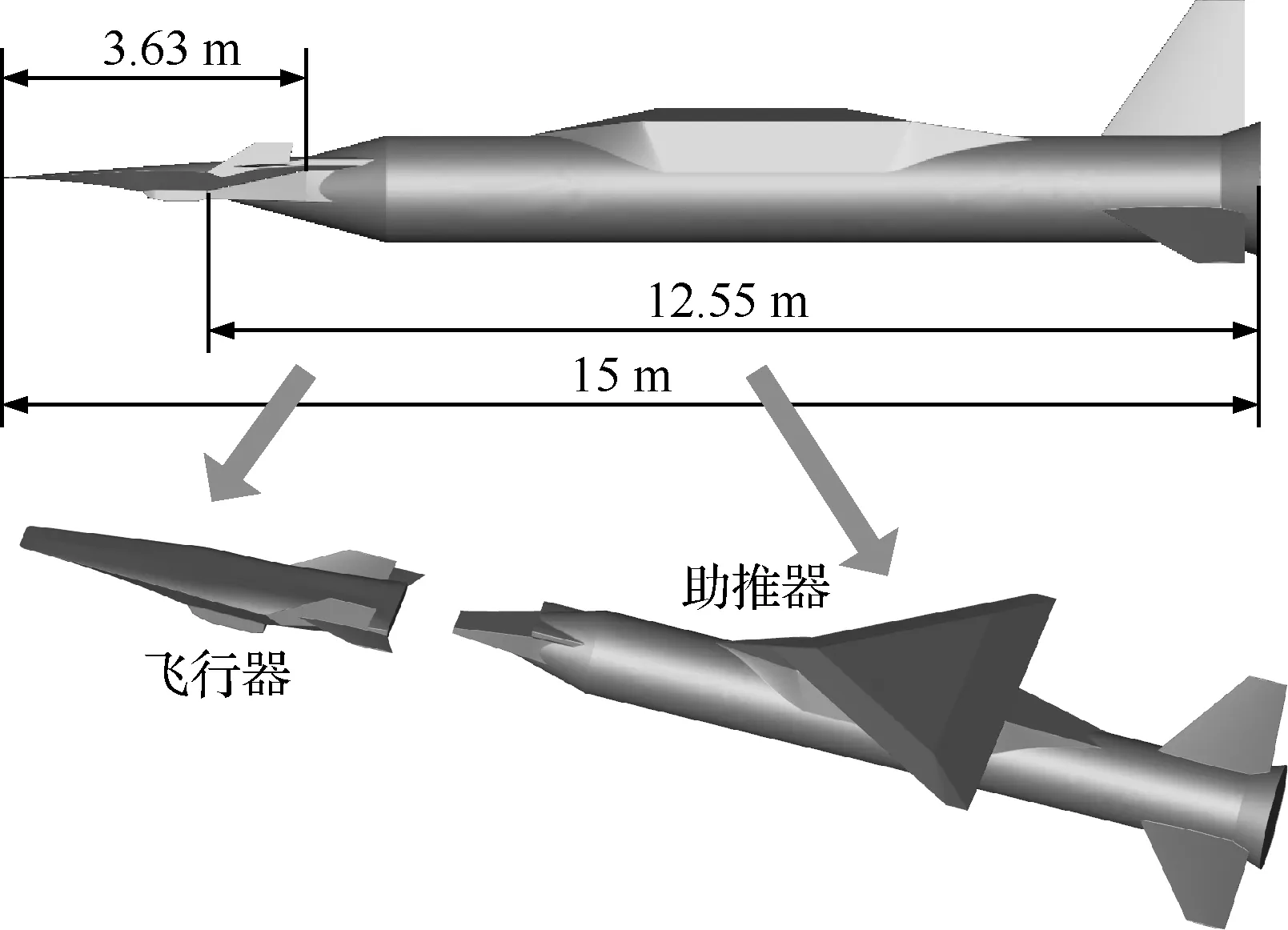
圖1 類X-43A飛行器實體模型Fig.1 Entity model of aerocraft similar to X-43A

圖2 類X-43A飛行器局部網格Fig.2 Local mesh of aerocraft similar to X-43A

圖3展示了類X-43A飛行器分離仿真計算域及邊界條件。其中，飛行器和助推器壁面采用無滑移絕熱壁，計算域入口邊界采用壓力遠場，來流均為超聲速流動，輸入參數包含馬赫數、靜壓、靜溫等，出口邊界設置為超聲速出口。

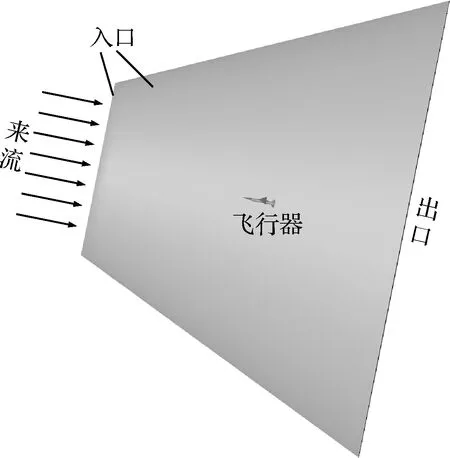
圖3 計算域和邊界條件Fig.3 Computational domains and boundary conditions

2 仿真驗證

選取美國空間實驗室進行的機翼/掛架模型WPFS分離投放作為仿真算例來驗證仿真方法的正確性。圖4為該模型示意圖，機翼為45°后掠的三角翼，采用NACA64A010翼型，半展長為6.6 m。機翼掛架位于機翼的中部，總長為2.3 m，寬0.15 m。彈身直徑為0.508 m，軸向長度為0.85 m，中間圓柱段長1.69 m，導彈尾部布置4片X形分布的尾翼。

圖4 機翼掛載模型示意圖Fig.4 Schematic diagram of wing mounting model

為了使彈體與掛架迅速分離，在掛載彈兩端施加大小分別為10 675.7 N和427 02.9 N的彈射力，掛載彈在彈射力、重力和氣動力的作用下運動，掛載彈的特性參數和仿真工況如表1所示。

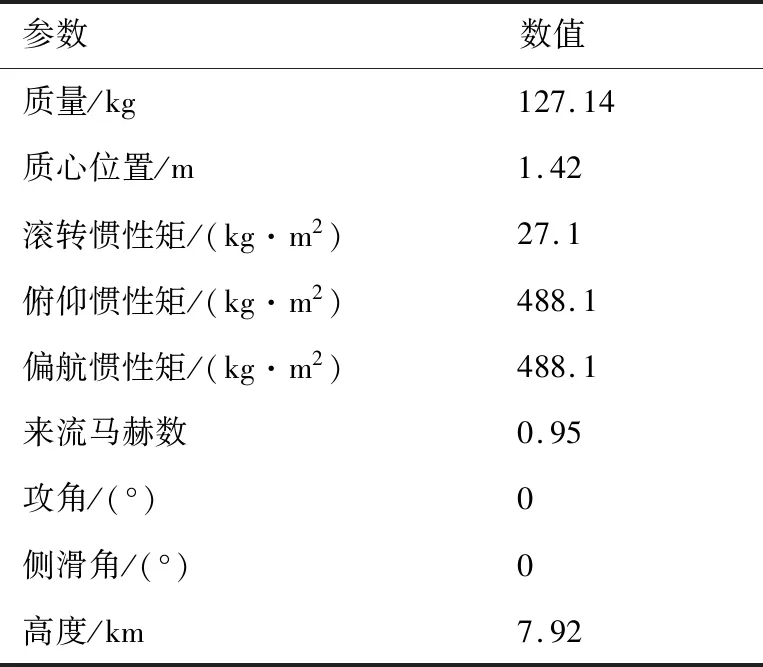
表1 掛載彈質量特性參數及仿真工況Table 1 Mass characteristic parameters and simulation conditions of mounted projectiles

利用以上仿真工況，開展機翼/掛載分離仿真，首先計算該工況下的定常流場，將其作為分離時刻的初場，時間步長取0.5 ms。圖5展示了不同分離時刻質心在、、3個方向的位移，其中線為仿真結果，點為試驗結果，可以看出二者吻合較好，驗證了仿真方法能夠對分離問題進行有效模擬。

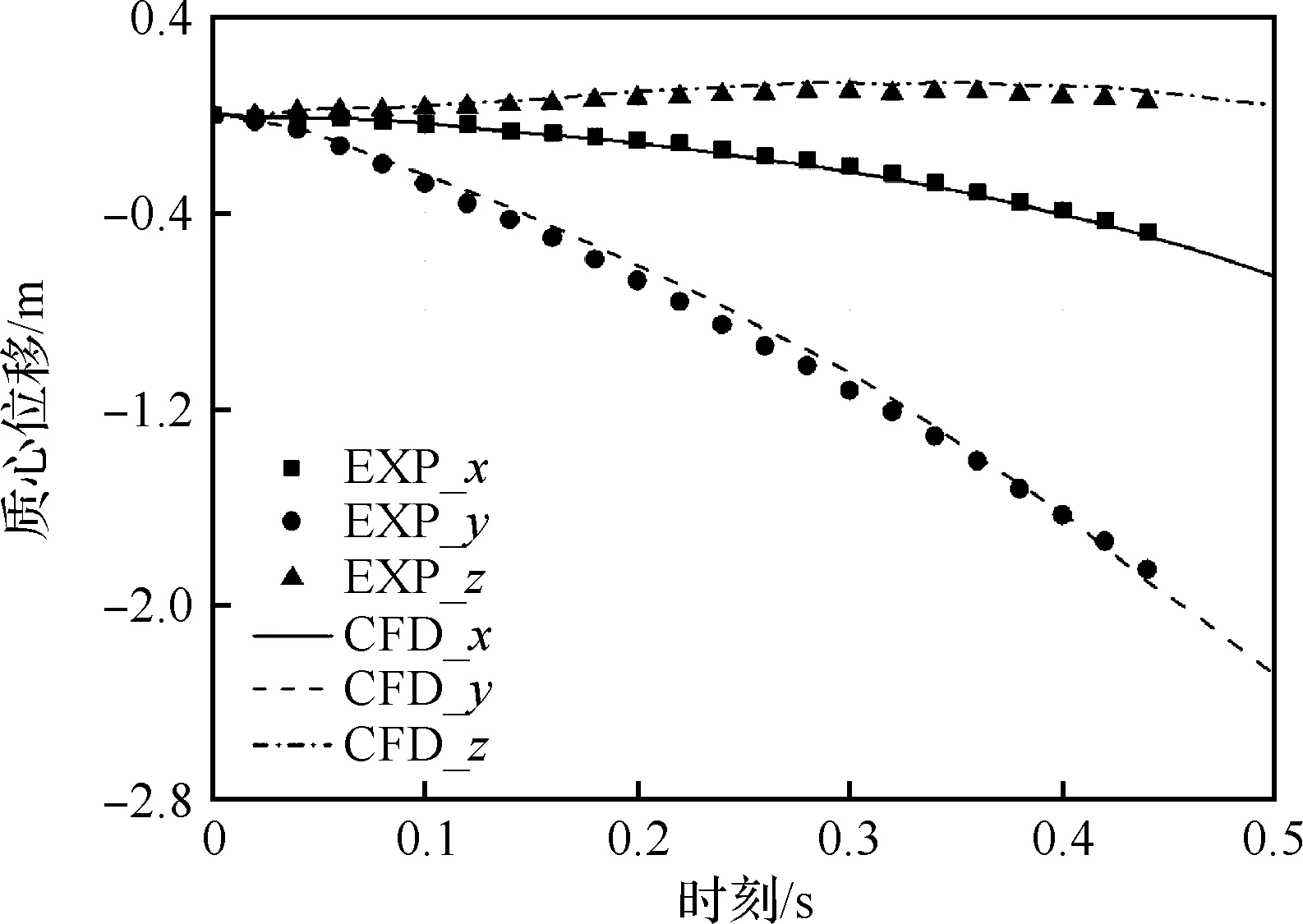
圖5 質心位移隨分離時刻變化Fig.5 Variation of centroid with separation time

另外，為了評估分離間隙對仿真結果的影響,分別對0.5 mm和1.0 mm分離間隙條件下的分離工況進行了分析，重點對比其對軸向、法向分離距離的影響，結果如圖6所示。可以看出，分離間隙分別為0.5 mm、1.0 mm情況下的軸向和法向相對距離吻合較好，分離間隙對于分離仿真結果基本無影響。

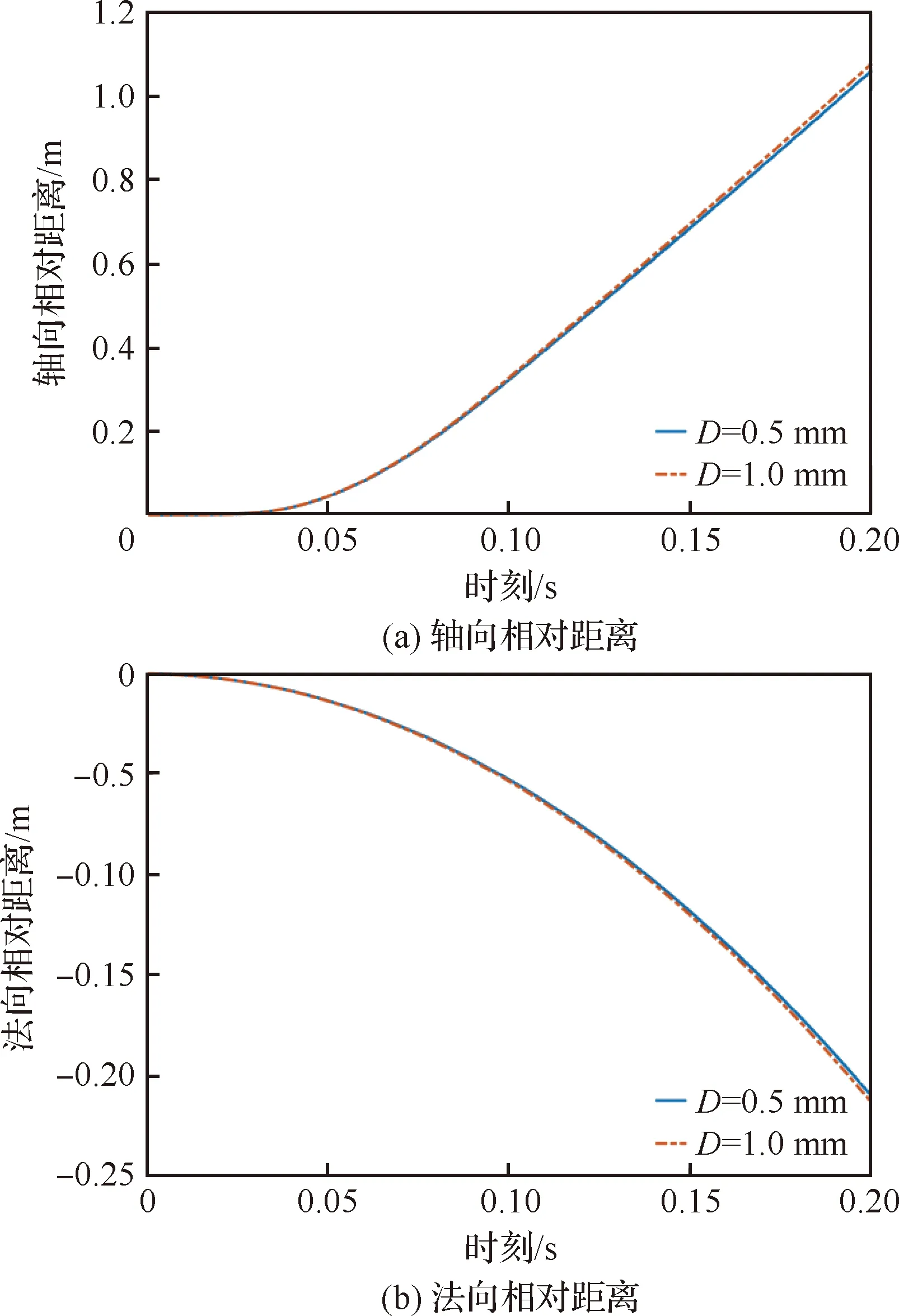
圖6 分離間隙分別為0.5 mm, 1.0 mm情況下相對距離隨分離時刻的變化Fig.6 Relative distances between aerocraft and assistor with separation gap of 0.5 mm and 1.0 mm

3 結果分析

X-43A的分離是在級間連接爆炸螺栓解鎖后，首先在液壓桿的彈射力作用下實施主動推離，彈射力隨分離時間的變化如圖7所示，在20 ms開始后彈射力迅速增大至約50 kN，隨后彈射力逐漸降低，直至98 ms時降為0 N；隨后飛行器和助推器在氣動力、重力作用下實現分離。分離過程受很多參數影響，如分離速度、高度、姿態角等，下面首先對分離過程典型流場進行分析，之后重點討論攻角、彈射力的影響。分離過程沖壓發動機進氣道處于封閉狀態，分離初始狀態參數設置如下：速度2 167 m/s，高度28.96 km，靜壓1 398.8 Pa，靜溫225.48，彈道傾角0°。

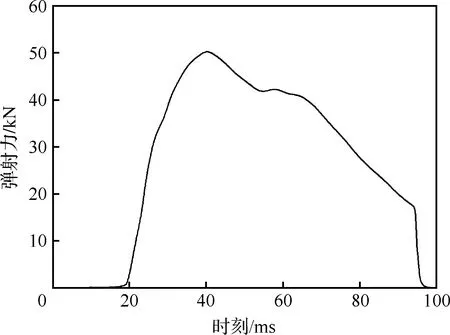
圖7 彈射力隨分離時刻的變化Fig.7 Variation of ejection force with separation time

3.1 典型流場

圖8展示了0°攻角情況下，飛行器與助推器在200 ms 分離時間內典型的馬赫數分布和流場情況。在分離初始時刻，沖壓發動機前端在高超聲速來流情況下形成較強的弓形激波，而助推器與飛行器底部和尾端面相接，其間基本沒有流體流動，當分離時刻達到50 ms，二者連接面逐漸分開，此時流動由縫隙流逐漸變為小通道流；隨著分離時刻達到100 ms，分離間隙進一步增加，級間連接處于飛行器的尾流區，分離間隙渦流強度逐漸增大，此時，飛行器和助推器之間的干擾主要來源于渦流。

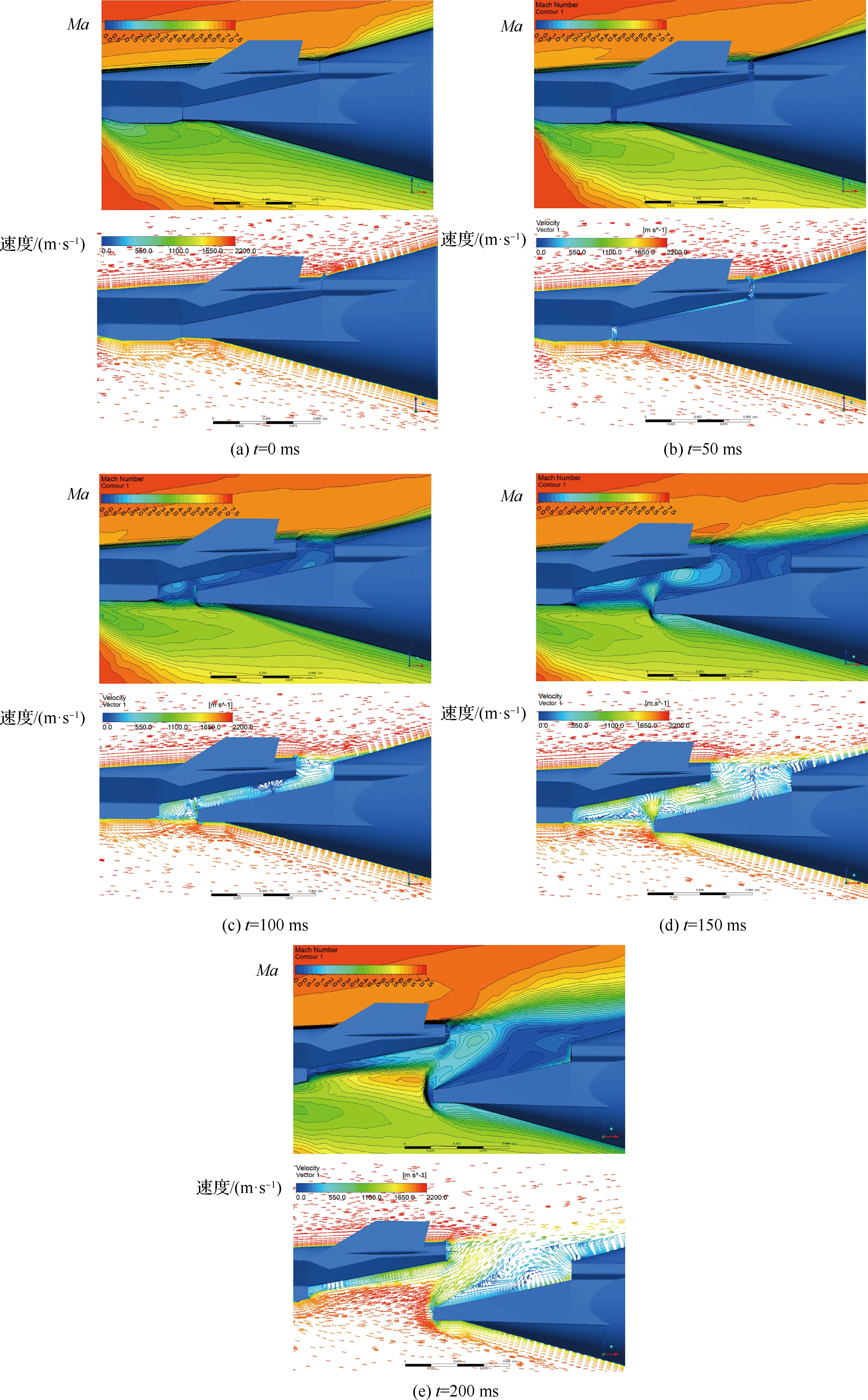
圖8 不同分離時刻類X-43A飛行器和級間連接處馬赫數和流線分布Fig.8 Distribution of Mach number and streamlines between aerocraft and assistor at different separation time

當分離時刻達到150 ms時，級間連接前端逐漸脫離飛行器尾流區，并開始出現弓形脫體激波，分離間隙流場在尾流區和弓形激波的作用下呈現復雜的流場分布，最顯著的流場結構在飛行器底部出現3個明顯的渦流區；當分離時刻達到200 ms 時，級間連接前端基本脫離飛行器尾流區，并暴露在自由來流中，形成完整的弓形激波，從而限制了尾流渦系的發展，使飛行器底部的氣流方向向機身下表面偏轉，并在級間連接斜面處形成一個較大的渦流區，此時分離區的干擾來源于級間連接前緣誘導激波和渦流的共同作用。隨著分離間距進一步增大，級間連接前緣的弓形激波進一步增強，而飛行器與助推器之間的干擾則會逐漸減弱。

3.2 攻角影響

圖9展示了攻角對飛行器和助推器質心軸向和法向相對距離的影響。假設初始時刻二者的相對距離為0 m，由圖可知，隨著分離時刻的推進，軸向相對距離逐漸增大，但隨攻角變化較小。圖9(b) 展示了攻角對質心法向相對距離的影響，可以看到，隨著初始分離攻角由2°減小到-2°，法向相對距離迅速增大。200 ms分離時刻，2°攻角情況下質心相對距離約0.08 m，-2°攻角情況下增大到0.34 m，對于類X-43A飛行器高超聲速分離而言，需要飛行器和助推器的軸向和法向距離快速增大到安全距離，此時，采用小攻角或者負攻角更有利于安全分離。

圖9 不同初始攻角情況下相對距離隨分離時刻的變化Fig.9 Relative distances between aerocraft and assistor at different initial angles of attack

圖10展示了150 ms分離時刻，初始分離攻角分別為-2°和2°情況下分離間隙及馬赫數分布的對比情況。由圖可知，2°攻角相較于-2°攻角情況下，飛行器和助推器均向+軸方向移動，但助推器移動距離更大，因此二者的法向間隙相對較小。對其進一步分析，比較了不同攻角下飛行器和助推器所受法向力，如圖11所示，可以看到助推器法向力受攻角的影響更加顯著，隨著攻角的變化，助推器法向力變化率為飛行器的5倍以上，而助推器的質量僅約為飛行器的兩倍，故正攻角下助推器沿+軸方向運動更加明顯，這與助推器大三角升力面有關。

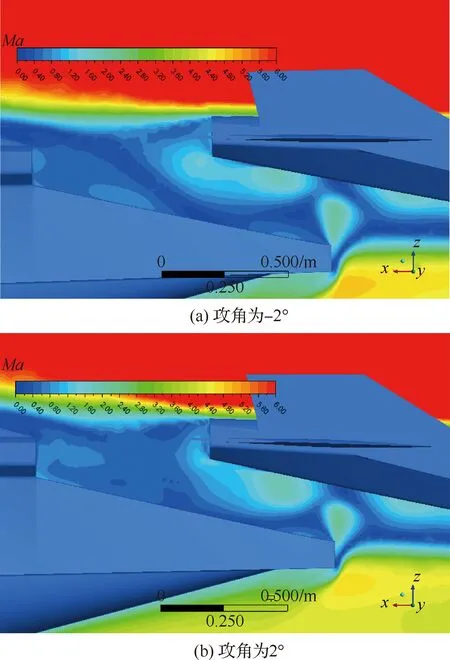
圖10 150 ms分離時刻分離間隙及其馬赫數分布Fig.10 Separation gap and Mach number distribution at 150 ms separation time

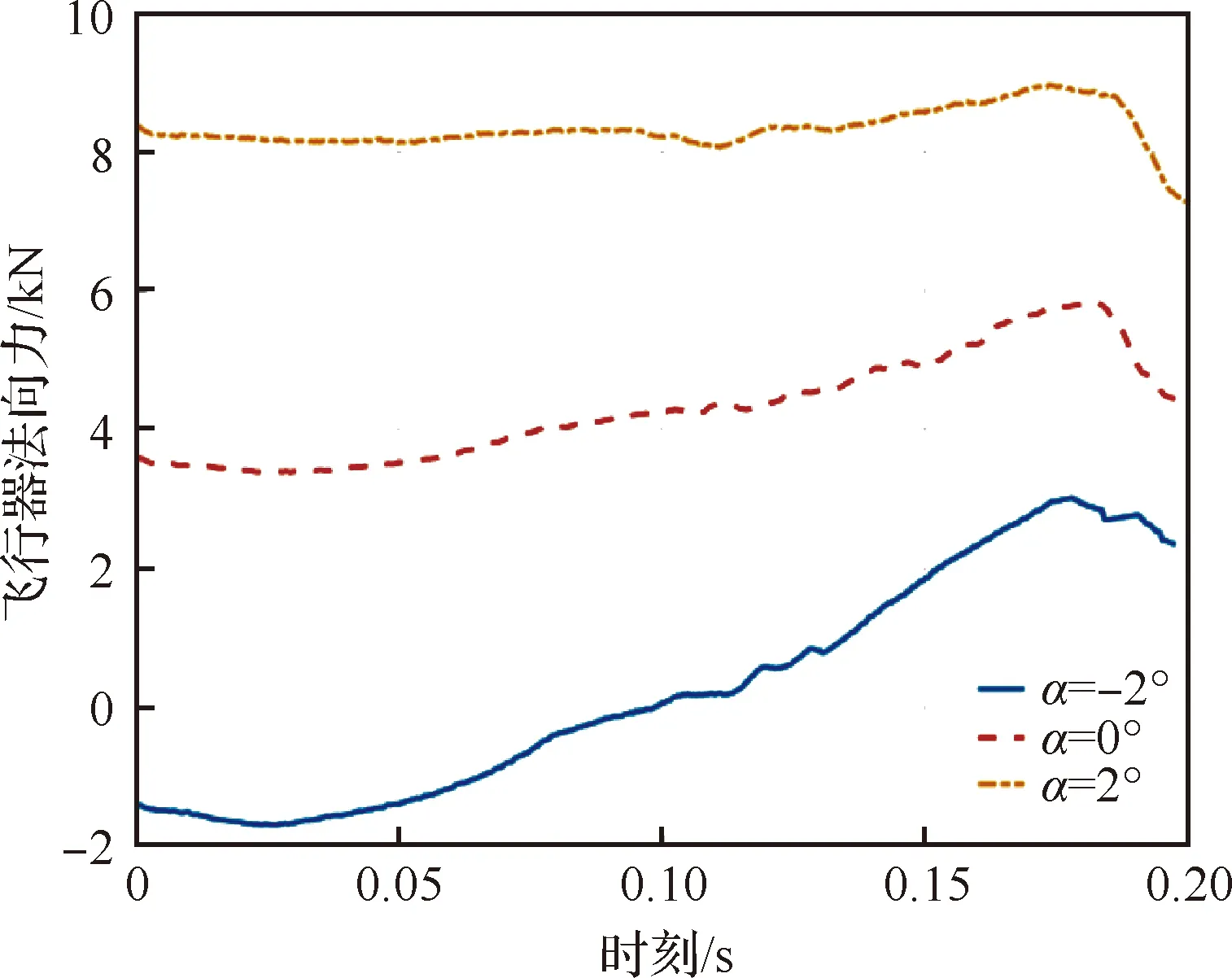
圖11 不同分離攻角情況下飛行器和助推器所受法向力Fig.11 Normal force on aerocraft and assistor at different angles of attack

圖12展示了飛行器攻角隨初始分離攻角的變化情況，由圖可知，隨著分離時間的推進，3種不同初始攻角下類X-43A飛行器均呈現抬頭趨勢，且負攻角情況下飛行器抬頭更加明顯，這緣于-2°～2°攻角下飛行器處于靜穩定狀態，而此時飛行器的配平攻角大于2°，因此分離后飛行器攻角會向配平攻角運動，且距離配平攻角越遠運動速度越大。

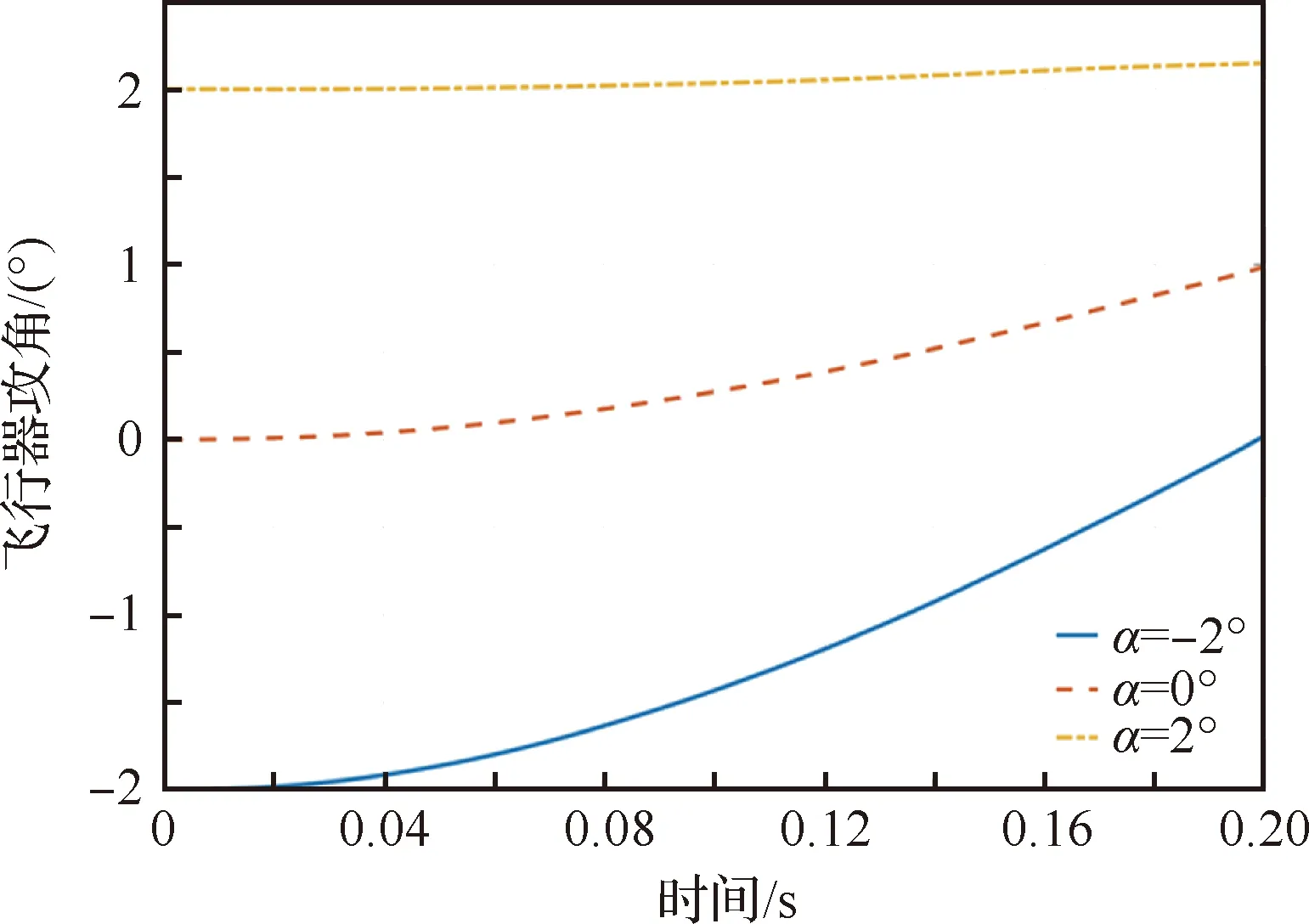
圖12 飛行器攻角隨初始攻角的變化情況Fig.12 Variation of aerocraft angle of attack with initial angle of attack

3.3 彈射力影響

為了研究彈射力對類X-43A飛行器和助推器的影響，對基準彈射力(圖7)和兩倍彈射力作用下的分離過程進行了仿真，并對比分析了其對軸向和法向相對距離的影響，如圖13所示。由圖可知，彈射力對于軸向相對距離影響較大，這主要是由于彈射力分別作用于飛行器和助推器，較大的彈射力使二者的相對分離速度快速增大，隨著分離時間的推進軸向相對距離越來越大，0.2 s時相差約1 m，由此可知，較大彈射力更有助于飛行器軸向的分離，而圖13(b)顯示彈射力對法向相對距離基本無影響。

圖13 不同彈射力情況下相對距離隨分離時刻的變化Fig.13 Relative distances between aerocraft and assistor with different ejection forces

圖14展示了在不同彈射力情況下，飛行器分離攻角隨分離時間的變化。由圖可知，在0.15 s分離時間內，彈射力對飛行器攻角基本無影響，而當分離時間超過0.15 s后，兩倍彈射力作用下飛行器的攻角迅速增大。其原因在于0.15 s分離時刻，兩倍彈射力作用下的飛行器與助推器質心軸向相對距離已達1.3 m，飛行器尾部底面基本脫離級間干擾區，并產生低壓回流區，在尾部上下表面的壓差作用下產生較大的抬頭力矩，而基準彈射力作用下的飛行器尾部底面此時還未脫離干擾區，其上下表面壓差變化不明顯。

圖14 不同彈射力情況下飛行器攻角隨分離時刻的變化Fig.14 Variation of aerocraft angle of attack with separation time with different ejection forces

4 結 論

以類X-43A飛行器為研究對象，基于網格變形/局部網格重構的方法，對高超聲速飛行器級間分離過程進行了仿真分析。為了驗證仿真方法的正確性，選取WPFS投放試驗作為驗證算例，結果表明仿真和試驗結果吻合較好。

對分離過程中典型流場分析表明，分離間隙的流動由縫隙流逐漸轉化為通道流，且在分離初期存在顯著的渦流區，隨著級間連接前端脫離飛行器尾流區，在其前方形成完整的弓形激波，從而限制了尾流渦系的發展，整個分離過程受到渦流和激波雙重干擾作用。

通過對攻角的影響分析可知：隨著攻角由2°減小到-2°，法向相對距離迅速由0.08 m增大到0.34 m，而軸向相對距離基本無變化，因此對于類X-43A高超聲速飛行器采用小攻角或者負攻角更有助于分離；另外，3種不同初始攻角下飛行器均呈現抬頭趨勢，且在負攻角情況下抬頭更加明顯。

對分離彈射力的比較分析可知，彈射力對于軸向相對距離有較大影響，0.2 s分離時刻，兩倍彈射力較基準彈射力作用下產生的軸向相對距離大約1 m；在分離初始0.15 s內，彈射力對飛行器攻角基本無影響，而當分離時間大于0.15 s后，兩倍彈射力作用下飛行器的攻角迅速增大，這緣于較大的分離彈射力使飛行器尾部底面更早地脫離級間干擾區，從而產生較大的抬頭力矩。