艉斜浪下船舶傾覆特性直接CFD 數(shù)值模擬

劉李為，余嘉威，馮大奎*，張志國(guó)，陳美霞

1 華中科技大學(xué) 船舶與海洋工程學(xué)院，湖北 武漢 430074

2 華中科技大學(xué) 船舶和海洋水動(dòng)力湖北省重點(diǎn)實(shí)驗(yàn)室，湖北 武漢 430074

0 引 言

水面艦船在隨浪或艉斜浪中航行時(shí)，由于遭遇周期的增大，會(huì)使船舯位于波浪波峰處的時(shí)間變長(zhǎng)，致使其穩(wěn)性力臂顯著降低，進(jìn)而導(dǎo)致穩(wěn)性失效模式的發(fā)生。這一失穩(wěn)模式被定義為純穩(wěn)性喪失，是船舶在波浪中典型的3 種傾覆模式（參數(shù)橫搖、純穩(wěn)性喪失和騎浪橫甩）之一[1]，涉及非線(xiàn)性橫搖運(yùn)動(dòng)、非線(xiàn)性復(fù)原力矩、非線(xiàn)性波浪力矩及其與船體的相互作用等強(qiáng)非線(xiàn)性動(dòng)力學(xué)問(wèn)題[2]。因此，由純穩(wěn)性喪失引發(fā)的船舶傾覆現(xiàn)象成為國(guó)際海事組織（IMO）針對(duì)船舶第二代完整穩(wěn)性的研究問(wèn)題之一。

在IMO 船舶與設(shè)計(jì)建造分委會(huì)（SDC）第四次會(huì)議中，完整船舶典型非線(xiàn)性失穩(wěn)模式的直接穩(wěn)性評(píng)估方法成為關(guān)注的重點(diǎn)。直接穩(wěn)性評(píng)估方法的建立能夠以更加精確的方式考慮所有相關(guān)因素，可以有效實(shí)現(xiàn)不同船舶的安全隱患評(píng)估，這在船舶設(shè)計(jì)階段是較為重要的。目前，國(guó)內(nèi)外有部分學(xué)者針對(duì)純穩(wěn)性喪失的預(yù)報(bào)方法以及運(yùn)動(dòng)特性進(jìn)行了較為深入的研究。朱軍等[3]針對(duì)船舶在波浪中的大傾角穩(wěn)性問(wèn)題，計(jì)算得到了規(guī)則波浪中船舶的穩(wěn)性變化規(guī)律，結(jié)果顯示船舶在正橫浪與斜浪條件下穩(wěn)性大幅度喪失的主要原因是波面相對(duì)船體橫剖面的不對(duì)稱(chēng)性。魯江等[4]構(gòu)建了一種縱蕩?垂蕩?橫搖?縱搖四自由度的耦合運(yùn)動(dòng)模型，其運(yùn)用該模型對(duì)隨浪規(guī)則波中的船舶穩(wěn)性喪失進(jìn)行直接評(píng)估，分析了縱蕩運(yùn)動(dòng)對(duì)純穩(wěn)性喪失預(yù)報(bào)的影響。Umeda 等[5]基于一種縱蕩?橫蕩?橫搖?艏搖四自由度的耦合運(yùn)動(dòng)模型，對(duì)艉斜浪中船舶的純穩(wěn)性喪失以及傾覆現(xiàn)象進(jìn)行了模擬。Lu 等[6]針對(duì)艉斜浪中船舶的純穩(wěn)性喪失問(wèn)題分別進(jìn)行了模型試驗(yàn)與六自由度數(shù)學(xué)模型預(yù)報(bào)研究，并進(jìn)一步闡明了艉斜浪中船舶艏搖與橫搖之間耦合作用的重要性。

以上研究主要是以基于勢(shì)流理論的數(shù)學(xué)模型為預(yù)報(bào)方法，通過(guò)模型試驗(yàn)，將船舶操縱運(yùn)動(dòng)水動(dòng)力導(dǎo)數(shù)、線(xiàn)性以及非線(xiàn)性橫搖阻尼的測(cè)量作為參數(shù)輸入來(lái)對(duì)船舶在波浪中的失穩(wěn)運(yùn)動(dòng)進(jìn)行直接評(píng)估。由IMO 對(duì)船舶典型失穩(wěn)模式直接評(píng)估方法的建議與要求可知，穩(wěn)性直接評(píng)估方法需要能對(duì)波浪中船舶穩(wěn)性變化、橫搖周期特性、主參數(shù)共振特性、騎浪平衡、波浪中的轉(zhuǎn)艏特性、多自由度耦合運(yùn)動(dòng)以及艉斜浪中的直航特性等水動(dòng)力性能實(shí)現(xiàn)可靠的模擬。基于全時(shí)域黏性流的數(shù)值模擬（CFD）方法正好能夠滿(mǎn)足上述要求，且無(wú)需依據(jù)試驗(yàn)測(cè)量或是經(jīng)驗(yàn)公式估計(jì)的數(shù)據(jù)作為參數(shù)輸入，因此可以考慮將其應(yīng)用至船舶非線(xiàn)性失穩(wěn)模式的直接評(píng)估中。

隨著高性能計(jì)算技術(shù)的飛速發(fā)展，直接CFD預(yù)報(bào)方法已能應(yīng)用到艦船復(fù)雜水動(dòng)力性能研究中。目前，CFD 方法已被用于船舶的回轉(zhuǎn)運(yùn)動(dòng)[7]、停船操縱[8]、騎浪運(yùn)動(dòng)[9]以及參數(shù)橫搖現(xiàn)象[10]的直接模擬，說(shuō)明直接模擬純穩(wěn)性喪失這類(lèi)集船舶操縱性與耐波性于一體的強(qiáng)非線(xiàn)性問(wèn)題已成為可能。因此，本文將基于CFD 方法對(duì)帶螺旋槳、帶舵的自航船舶在艉斜浪下保持航向操縱運(yùn)動(dòng)進(jìn)行直接模擬，預(yù)報(bào)典型失穩(wěn)模式下船舶的六自由度耦合運(yùn)動(dòng)，并對(duì)船舶的失穩(wěn)運(yùn)動(dòng)及傾覆特性進(jìn)行直接評(píng)估。

1 數(shù)值方法

1.1 流場(chǎng)求解方法

使用課題組自主開(kāi)發(fā)的艦船水動(dòng)力CFD 求解器HUST-Ship 進(jìn)行數(shù)值仿真計(jì)算，通過(guò)對(duì)非定常RANS 方程的求解來(lái)獲取流場(chǎng)特征，然后采用有限差分法進(jìn)行數(shù)值離散，并基于結(jié)構(gòu)網(wǎng)格模型在每個(gè)網(wǎng)格點(diǎn)上對(duì)差分方程進(jìn)行求解。控制方程如下：

1.2 重疊網(wǎng)格方法

CFD 求解器在對(duì)流場(chǎng)壓力速度特性進(jìn)行求解的同時(shí)，也會(huì)耦合剛體六自由度運(yùn)動(dòng)方程來(lái)進(jìn)行力和力矩以及運(yùn)動(dòng)的實(shí)時(shí)預(yù)報(bào)。考慮到船舶在波浪中的大幅度運(yùn)動(dòng)、船后螺旋槳旋轉(zhuǎn)以及艉舵操縱運(yùn)動(dòng)特性，在CFD 求解器中應(yīng)用了重疊網(wǎng)格技術(shù)（HUST-Overset），用以實(shí)現(xiàn)船體網(wǎng)格模型與計(jì)算域之間的大幅相對(duì)運(yùn)動(dòng)，以及自航船舶船、槳、舵多級(jí)耦合運(yùn)動(dòng)的數(shù)值仿真。另一方面，重疊網(wǎng)格模塊的應(yīng)用允許在前處理網(wǎng)格生成過(guò)程中單獨(dú)對(duì)不同的對(duì)象（計(jì)算域、船體、各附體以及推進(jìn)器）進(jìn)行網(wǎng)格劃分，并通過(guò)重疊區(qū)域的構(gòu)建實(shí)現(xiàn)網(wǎng)格之間的組裝和數(shù)值計(jì)算模型的生成，這大大降低了全附體船舶結(jié)構(gòu)化網(wǎng)格的生成難度，提高了結(jié)構(gòu)化網(wǎng)格的質(zhì)量。

重疊網(wǎng)格模塊的重點(diǎn)是生成不同網(wǎng)格塊之間的物面重疊以及體重疊區(qū)域。在HUST-Overset中，首先通過(guò)洞映射方法進(jìn)行洞點(diǎn)的處理以及附近插值點(diǎn)的識(shí)別，包括洞邊界點(diǎn)與外邊界點(diǎn)；然后，基于交替數(shù)字樹(shù)算法（ADT）為插值點(diǎn)搜尋相對(duì)應(yīng)的貢獻(xiàn)點(diǎn)，其中插值點(diǎn)與貢獻(xiàn)點(diǎn)之間通過(guò)三線(xiàn)性插值方法進(jìn)行流場(chǎng)數(shù)據(jù)的傳遞；最后，基于插值點(diǎn)與貢獻(xiàn)點(diǎn)之間的體積匹配及點(diǎn)距離進(jìn)行重疊區(qū)域的優(yōu)化，在保證網(wǎng)格單元體積匹配且至少2 層網(wǎng)格互相重疊的前提下盡可能縮小重疊區(qū)域的面積。

1.3 操縱控制模塊

基于動(dòng)態(tài)重疊網(wǎng)格方法，自航船舶在波浪中進(jìn)行操縱運(yùn)動(dòng)過(guò)程中的船、槳、舵多級(jí)耦合運(yùn)動(dòng)得以實(shí)現(xiàn)。在CFD 求解器中集成了操縱運(yùn)動(dòng)控制模塊，可以實(shí)現(xiàn)自航船舶在波浪條件下的航向保持操縱運(yùn)動(dòng)，然后通過(guò)使用PID 控制技術(shù)對(duì)螺旋槳轉(zhuǎn)速進(jìn)行控制來(lái)使船舶達(dá)到目標(biāo)航速，并以船舶艏向角為輸入對(duì)艉舵操縱角度進(jìn)行反饋控制，從而保證船舶不偏離目標(biāo)航向。基于PID 的控制形式如下：

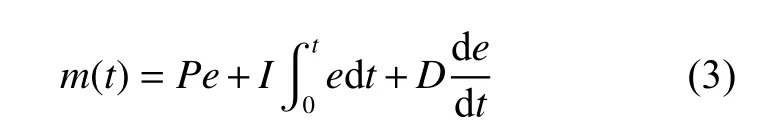
式中：P，I，D分別為比例項(xiàng)、積分項(xiàng)和微分項(xiàng)的控制常數(shù)；e為實(shí)測(cè)值與目標(biāo)值之間的差值。對(duì)于自航船舶在波浪條件下的航向保持運(yùn)動(dòng)，在計(jì)算過(guò)程中可通過(guò)不斷調(diào)整舵角角度來(lái)使船舶在航行過(guò)程中保持目標(biāo)航向。

1.4 移動(dòng)數(shù)值試驗(yàn)水池

在船舶大尺度操縱運(yùn)動(dòng)（例如，自由自航運(yùn)動(dòng)、回轉(zhuǎn)運(yùn)動(dòng)和Z 形操縱運(yùn)動(dòng)）的數(shù)值模擬過(guò)程中，如果類(lèi)似于物理試驗(yàn)水池一樣采用靜止的數(shù)值水池進(jìn)行仿真，會(huì)大大增加數(shù)值計(jì)算的網(wǎng)格量，從而降低計(jì)算速率。因此，可在CFD 求解器中采用隨船一起運(yùn)動(dòng)的移動(dòng)數(shù)值試驗(yàn)水池模型，以便節(jié)省數(shù)值水池網(wǎng)格量，提高數(shù)值計(jì)算的效率。

在移動(dòng)數(shù)值試驗(yàn)水池模型的實(shí)現(xiàn)過(guò)程中，將船舶主體網(wǎng)格和數(shù)值水池網(wǎng)格分別予以處理：通過(guò)計(jì)算得到船舶受力和力矩，結(jié)合船舶六自由度運(yùn)動(dòng)方程的求解得到船舶在大地坐標(biāo)系下的姿態(tài)和位置變化，提取船舶的縱蕩和橫蕩速度以及位移信息，并賦值于數(shù)值試驗(yàn)水池上，從而保證在數(shù)值模擬過(guò)程中數(shù)值水池與船舶主體網(wǎng)格之間的縱向和橫向相對(duì)位移足夠小，具體實(shí)現(xiàn)流程圖如圖1 所示。在此過(guò)程中，可將速度入口造波方式與移動(dòng)數(shù)值水池模型進(jìn)行耦合處理，并將數(shù)值試驗(yàn)水池的速度入口邊界與入射波浪的浪向設(shè)置為始終保持垂直，用以保證數(shù)值試驗(yàn)水池在移動(dòng)過(guò)程中水池內(nèi)的數(shù)值波浪模擬精度不受影響。圖2直觀地示出了船舶在不同類(lèi)型操縱運(yùn)動(dòng)過(guò)程中數(shù)值波浪水池的移動(dòng)方式。

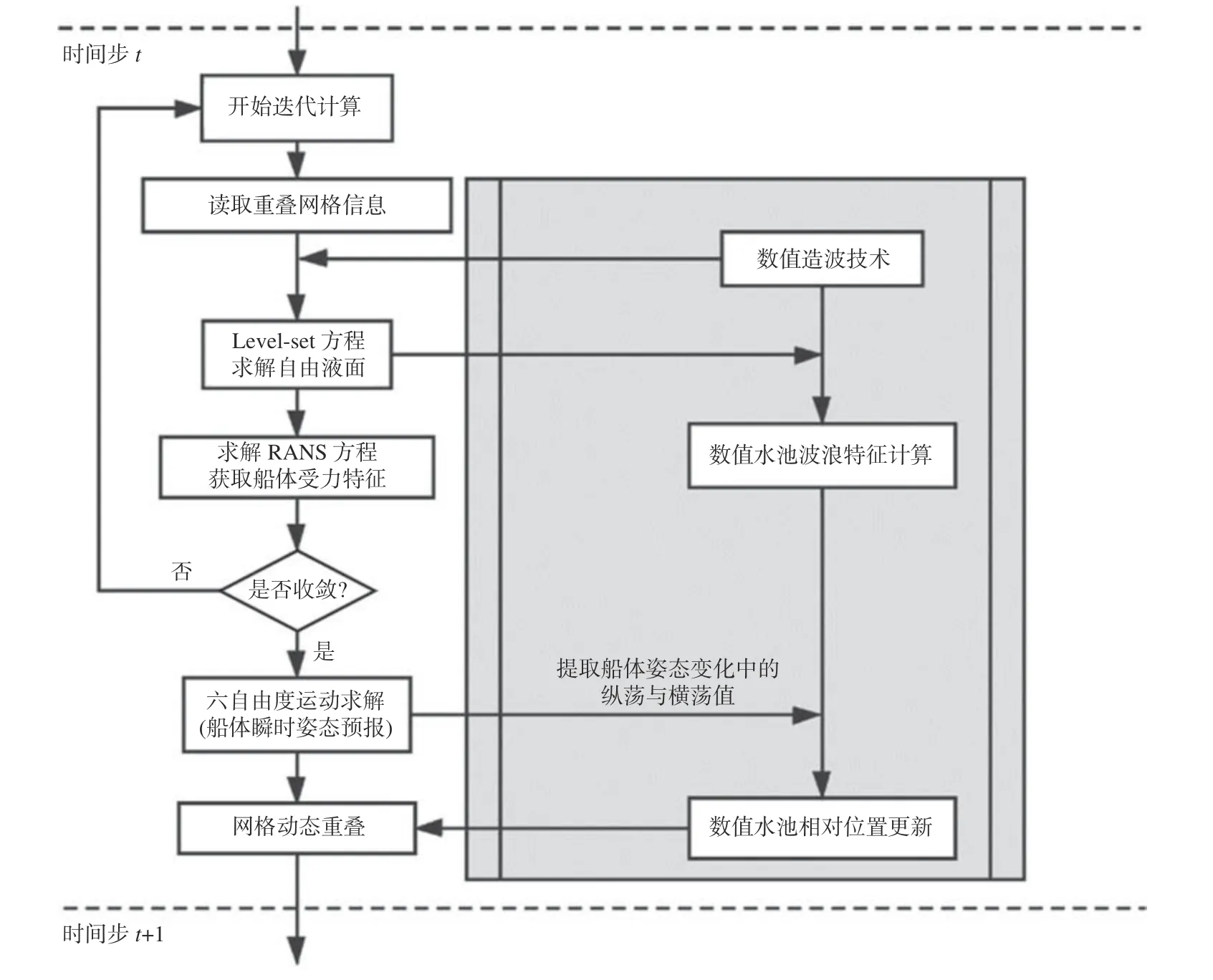
圖1 移動(dòng)數(shù)值波浪水池模型與船舶運(yùn)動(dòng)耦合求解流程圖Fig. 1 Flowchart of the coupling solution between the moving numerical wave tank and ship motions

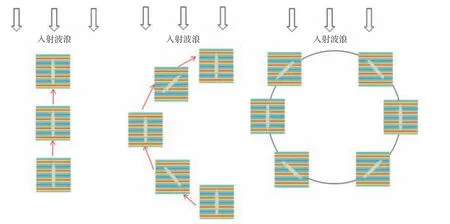
圖2 船舶不同操縱運(yùn)動(dòng)過(guò)程中數(shù)值波浪水池的移動(dòng)方式Fig. 2 The movement mode of the moving numerical wave tank during different ship maneuvering motions

2 計(jì)算對(duì)象與工況

選取全附體雙槳、雙舵的ONRT 船模為研究對(duì)象，該船模為被廣泛應(yīng)用于數(shù)值仿真算法驗(yàn)證的標(biāo)準(zhǔn)模型。文獻(xiàn)[6]以O(shè)NRT 自航船模為對(duì)象對(duì)其進(jìn)行了純穩(wěn)性喪失模型試驗(yàn)，相關(guān)的試驗(yàn)數(shù)據(jù)可用于驗(yàn)證本文CFD 方法的可靠性。模型的縮尺比為40.526，其幾何形狀如圖3 所示，主尺度如表1 所示。根據(jù)文獻(xiàn)[6]中的自航模試驗(yàn)工況，對(duì)自航船舶在30°艉斜浪規(guī)則波中的航向保持操縱運(yùn)動(dòng)進(jìn)行數(shù)值模擬，其中規(guī)則波波長(zhǎng)λ =1.25LWL，波高H= 0.05λ，波速C= 2.722 m/s，波浪頻率f= 0.573 Hz。船模航速為1.831 m/s，對(duì)應(yīng)的弗勞德數(shù)Fr= 0.30。在數(shù)值模擬過(guò)程中考慮船舶的六自由度運(yùn)動(dòng)，并通過(guò)航向角反饋控制器不斷操控艉舵舵角來(lái)使船舶保持航向航行。

表1 ONRT 模型主尺度參數(shù)Table 1 Main parameters of ONRT model

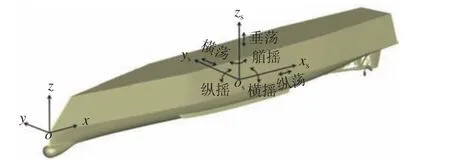
圖3 ONRT 模型幾何圖Fig. 3 Geometry of ONRT model

在數(shù)值模擬的前處理過(guò)程中，分別對(duì)計(jì)算域、船體以及各附體（呆木、艉舵、舭龍骨、軸系及螺旋槳）進(jìn)行結(jié)構(gòu)化網(wǎng)格劃分，計(jì)算域網(wǎng)格與數(shù)值模擬邊界條件的設(shè)置如圖4 所示。全附體模型網(wǎng)格如圖5 所示。運(yùn)用重疊程序HUST-Overset 實(shí)現(xiàn)網(wǎng)格組裝與重疊區(qū)域的生成，所建立的數(shù)值計(jì)算網(wǎng)格模型如圖6 所示。在進(jìn)行數(shù)值模擬之前，對(duì)螺旋槳網(wǎng)格進(jìn)行網(wǎng)格收斂性分析，具體的結(jié)果參見(jiàn)文獻(xiàn)[14]，從中可知中等數(shù)量網(wǎng)格與密網(wǎng)格方案下的螺旋槳敞水特性預(yù)報(bào)結(jié)果差別較小，且與試驗(yàn)結(jié)果間的誤差均小于2.5%，而稀疏網(wǎng)格方案下螺旋槳敞水特性預(yù)報(bào)結(jié)果與試驗(yàn)結(jié)果間的誤差則為6%。由于全附體模型網(wǎng)格收斂性分析結(jié)果與螺旋槳網(wǎng)格收斂性分析結(jié)果的現(xiàn)象一致，因此選用中等數(shù)量網(wǎng)格方案進(jìn)行數(shù)值模擬。根據(jù)網(wǎng)格收斂性結(jié)果選取了最終適用的計(jì)算網(wǎng)格模型，網(wǎng)格節(jié)點(diǎn)總數(shù)量為978 萬(wàn)。

圖4 計(jì)算域網(wǎng)格Fig. 4 Grid of the computational domain

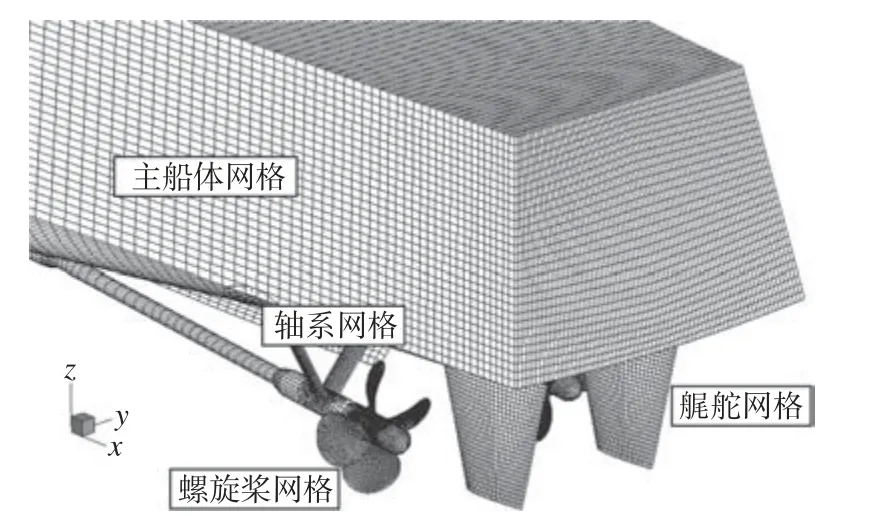
圖5 全附體模型網(wǎng)格Fig. 5 Grid of the fully appended ship model

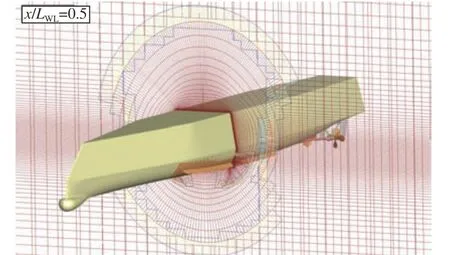
圖6 數(shù)值計(jì)算網(wǎng)格模型Fig. 6 Numerical grid model

3 數(shù)值模擬結(jié)果分析

基于CFD 求解器HUST-Ship，耦合動(dòng)態(tài)重疊網(wǎng)格方法，對(duì)ONRT 模型在30°艉斜浪規(guī)則波（λ = 1.25LWL，H= 0.05λ）中的典型失穩(wěn)模式純穩(wěn)性喪失進(jìn)行數(shù)值模擬。在數(shù)值模擬過(guò)程中放開(kāi)了船舶的六自由度運(yùn)動(dòng)，并通過(guò)航向角反饋控制器不斷操控艉舵舵角來(lái)使船舶保持航向航行。在文獻(xiàn)[15]中，IIHR 水池運(yùn)用PID 控制技術(shù)中的比例控制器（P= 1，I=D= 0）對(duì)ONRT 模型在不同浪向下的航向保持進(jìn)行了試驗(yàn)，并取得了良好的效果。因此，本文進(jìn)行數(shù)值模擬的控制設(shè)定將與該試驗(yàn)中的控制方法一致。

由文獻(xiàn)[6] 中的自航模試驗(yàn)結(jié)果可知，模型在Fr達(dá)到0.30 時(shí)發(fā)生了強(qiáng)烈的穩(wěn)性喪失現(xiàn)象，并導(dǎo)致船舶出現(xiàn)了傾覆。因此，在數(shù)值模擬過(guò)程中將參考該工況，固定螺旋槳轉(zhuǎn)速以使模型航速與試驗(yàn)保持一致。數(shù)值計(jì)算工作在國(guó)家超級(jí)計(jì)算廣州中心高性能計(jì)算機(jī)集群上進(jìn)行，共采用120 個(gè)計(jì)算核心進(jìn)行了并行計(jì)算，所花費(fèi)的總計(jì)算時(shí)間約208 h，對(duì)應(yīng)的CPU 計(jì)算時(shí)間為2.5 萬(wàn)計(jì)算機(jī)核時(shí)。圖7 所示為純穩(wěn)性喪失過(guò)程中船后周?chē)臏u結(jié)構(gòu)。模型在波浪中自由自航時(shí)航速的時(shí)歷曲線(xiàn)如圖8 所示（圖中，U為船舶航速）。由圖可知，在該工況下船舶的瞬時(shí)航速接近于波速在船長(zhǎng)方向的分量，這就意味著船舶與波浪之間的相對(duì)速度較小，即船舶在航行過(guò)程中，在波峰處的停留時(shí)間非常長(zhǎng)，導(dǎo)致船舶在艉斜浪中的穩(wěn)性長(zhǎng)時(shí)間降低。由于缺乏足夠的復(fù)原力，在持續(xù)的外部橫傾力矩作用下，船舶會(huì)發(fā)生純穩(wěn)性喪失現(xiàn)象，從而導(dǎo)致大幅度的非線(xiàn)性橫搖運(yùn)動(dòng)。

圖7 純穩(wěn)性喪失發(fā)生時(shí)船后周?chē)鷾u結(jié)構(gòu)Fig. 7 Vorticity structure around the ship stern when the pure loss of stability occurs

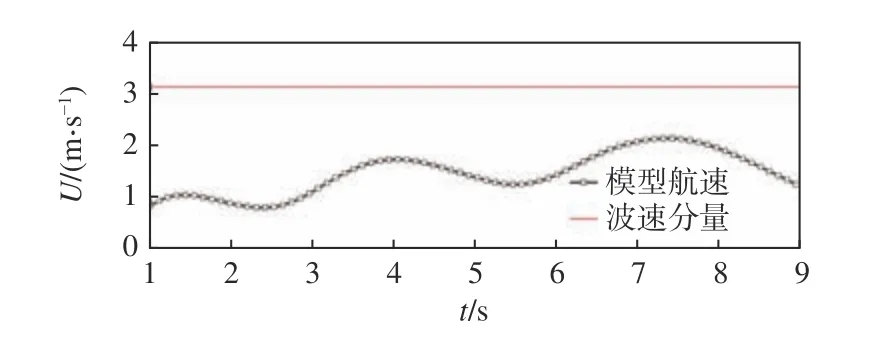
圖8 船舶航速時(shí)歷曲線(xiàn)Fig. 8 Time histories of the ship speed

圖9 所示為自航船舶在艉斜浪規(guī)則波中的縱蕩、橫蕩以及垂蕩運(yùn)動(dòng)時(shí)歷曲線(xiàn)（圖中，x，y，z分別代表縱蕩、橫蕩與垂蕩），船舶在螺旋槳的推進(jìn)作用下始終保持向前航行。圖10 所示為自航船舶在艉斜浪規(guī)則波中的橫搖、縱搖以及艏搖運(yùn)動(dòng)時(shí)歷曲線(xiàn)（圖中， ?，ψ，θ 分別為橫搖角、艏搖角和縱搖角）。由圖10 可知，船舶在持續(xù)的穩(wěn)性喪失情況下發(fā)生了大幅度的橫搖運(yùn)動(dòng)，最終，由于橫搖角過(guò)大而導(dǎo)致了傾覆現(xiàn)象的發(fā)生。與此同時(shí)，船舶的艏搖角也顯著增大，并與船舶橫搖運(yùn)動(dòng)發(fā)生了耦合作用。當(dāng)船舶橫搖角達(dá)90°時(shí)，其艏搖角達(dá)到了16°，這說(shuō)明船舶在穩(wěn)性喪失狀態(tài)下依靠操舵已無(wú)法有效控制船舶航向，從而導(dǎo)致了較為明顯的橫甩現(xiàn)象的發(fā)生。最終，純穩(wěn)性喪失、大幅度橫搖、劇烈的橫甩以及外部載荷的耦合作用導(dǎo)致了自航船舶的傾覆。

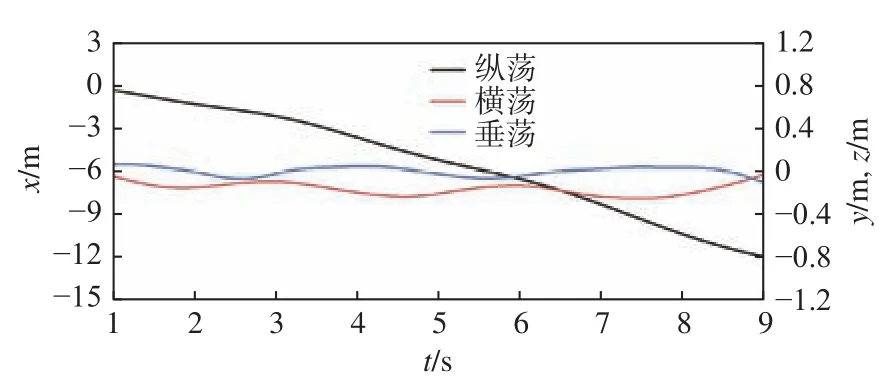
圖9 船舶縱蕩、橫蕩與垂蕩運(yùn)動(dòng)的時(shí)歷曲線(xiàn)Fig. 9 Time histories of the ship surge, sway, and heave motion

圖10 船舶橫搖、縱搖與艏搖運(yùn)動(dòng)的時(shí)歷曲線(xiàn)Fig. 10 Time histories of the ship roll, pitch, and yaw motion

為了進(jìn)行數(shù)值模擬可靠性的驗(yàn)證，將船舶橫搖、縱搖以及艏搖角時(shí)域信號(hào)的數(shù)值模擬結(jié)果（CFD）與文獻(xiàn)[6]中的模型試驗(yàn)數(shù)據(jù)（EFD）進(jìn)行了對(duì)比，結(jié)果如圖10 所示。由圖可知，CFD 與EFD結(jié)果之間吻合較好，且這2 種方法對(duì)船舶運(yùn)動(dòng)隨時(shí)間變化趨勢(shì)的預(yù)報(bào)非常一致，說(shuō)明采用CFD 方法模擬船舶失穩(wěn)運(yùn)動(dòng)與傾覆現(xiàn)象準(zhǔn)確性較高。

在CFD 數(shù)值模擬過(guò)程中，不同時(shí)刻下船舶姿態(tài)的實(shí)時(shí)變化及其周?chē)杂擅娴牟ㄐ稳鐖D11 所示，圖中，Te為波浪遭遇周期。由圖可以看出，艉斜浪的不對(duì)稱(chēng)性會(huì)造成船舶左右舷所受的外部載荷不同，從而導(dǎo)致船舶發(fā)生不對(duì)稱(chēng)的橫搖運(yùn)動(dòng)，船艏處的渦結(jié)構(gòu)同樣也表現(xiàn)出了不對(duì)稱(chēng)性。同時(shí)，由圖還可以發(fā)現(xiàn)，采用CFD 方法能準(zhǔn)確模擬出船舶因穩(wěn)性喪失而導(dǎo)致實(shí)時(shí)橫搖直至最終傾覆的過(guò)程，以及在橫搖過(guò)程中耦合發(fā)生的橫甩現(xiàn)象。這表明運(yùn)用CFD 方法能夠直接模擬船舶的失穩(wěn)運(yùn)動(dòng)與傾覆現(xiàn)象，且模擬結(jié)果已較為接近真實(shí)場(chǎng)景，有利于船舶典型失穩(wěn)模式直接評(píng)估工作的開(kāi)展。

圖11 不同時(shí)刻下船舶姿態(tài)的實(shí)時(shí)變化及其周?chē)杂擅娌ㄐ蜦ig. 11 The real-time change of ship attitude and the free surface wave around the ship at different time instances

4 結(jié) 語(yǔ)

本文基于黏性流理論建立了CFD 數(shù)值模擬方法，然后結(jié)合動(dòng)態(tài)重疊網(wǎng)格技術(shù)與操縱運(yùn)動(dòng)反饋控制模塊，對(duì)帶螺旋槳和帶舵的自航船舶ONRT在艉斜浪下保持航向操縱運(yùn)動(dòng)進(jìn)行了直接模擬，預(yù)報(bào)了純穩(wěn)性喪失失穩(wěn)模式下船舶的六自由度運(yùn)動(dòng)，并對(duì)船舶的傾覆特性進(jìn)行了直接評(píng)估。結(jié)果表明，運(yùn)用CFD 方法模擬船舶失穩(wěn)運(yùn)動(dòng)與傾覆現(xiàn)象可靠性和準(zhǔn)確性較高。

此外，CFD 數(shù)值模擬結(jié)果表明，船舶在持續(xù)的穩(wěn)性喪失情況下會(huì)發(fā)生大幅度的橫搖運(yùn)動(dòng)，最終會(huì)因橫搖角過(guò)大而導(dǎo)致傾覆現(xiàn)象的發(fā)生。同時(shí)，船舶的艏搖角也將顯著增大，說(shuō)明船舶在穩(wěn)性喪失狀態(tài)下依靠操舵已無(wú)法有效控制船舶航向，從而發(fā)生了較為明顯的橫甩現(xiàn)象，這也是船舶發(fā)生傾覆的關(guān)鍵因素之一。

未來(lái)，將借助直接CFD 數(shù)值模擬方法對(duì)不同航速下自航船舶在艉斜浪中的失穩(wěn)運(yùn)動(dòng)特性進(jìn)行分析與比較，并對(duì)船舶由純穩(wěn)性喪失引發(fā)的大幅度非線(xiàn)性失穩(wěn)運(yùn)動(dòng)的發(fā)生機(jī)理進(jìn)行研究。