實尺度船舶Z 形操縱運動及流場特性模擬

冀楠，錢志鵬，李浩然，萬德成

1 重慶交通大學 航運與船舶工程學院，重慶 400074

2 上海交通大學 船舶海洋與建筑工程學院，上海 200240

3 上海交通大學 海洋工程國家重點實驗室，上海 200240

4 上海交通大學 船海計算水動力學研究中心，上海 200240

0 引 言

船舶操縱性直接關系到實際營運的經濟性和船舶航行的安全性。歐盟海事安全局（ESMA）在2020 年發布的海上傷亡和事故年度報告中指出，因碰撞、接觸和擱淺事故造成的人員傷亡占所有海事事故的44%以上。自2002 年國際海事組織（IMO）頒布《船舶操縱性標準》決議[1]以來，更早、更好地評估船舶操縱性已成為船舶設計的一個重要方面。國際船模拖曳水池會議（ITTC）針對主流的船舶操縱性預報方法進行了匯總，主要有直接預報法、基于系統的研究方法和CFD 數值模擬方法[2]。

所謂基于系統的研究方法，是通過建立操縱性數學模型，利用預報的水動力系數/導數來獲得船舶操縱性指數，包括約束模試驗、自航模試驗及系統辨識方法預報等[3]。其中，約束模試驗方法是指對一定縮尺比的船模在拖曳水池中進行的大量強迫運動試驗，包括斜拖試驗、懸臂試驗、平面運動機構試驗以及圓周運動試驗。Ortolani 等[4-5]對某雙槳雙舵船進行了斜拖試驗，分析了螺旋槳在非設計工況下的載荷變化，并針對非定常流下的單槳葉載荷展開了細致的研究。自航模試驗方法是指在物理操縱水池中對一定縮尺比下的船體、螺旋槳和舵進行的標準操縱試驗，其通過控制螺旋槳轉速和操舵來實現船舶操縱運動，典型的標準操縱試驗有Z 形操縱試驗、自由回轉試驗等。自航模試驗作為一種傳統的試驗方法，被公認為是評價船舶操縱性能最可靠的一種方法，一些典型船型的操縱性試驗數據已非常完備[6-8]，但該方法成本昂貴、技術要求嚴格，需要具備較大的試驗水池。系統辨識方法主要包括最小二乘法、擴展卡爾曼濾波法、嶺回歸分析方法、神經網絡方法等。如何通過解決水動力導數的多重共線性問題來減少參數漂移是提高建模精度的關鍵[9]。Song 等[10]提出了一種多創新最小二乘算法，用來識別隨機梯度雙曲正切非線性，并基于實船海試數據對該算法進行了驗證，驗證結果顯示該算法具有良好的收斂性。隨著高性能計算機的快速發展，CFD 數值模擬方法在船舶領域得到了廣泛應用。與傳統理論相比，CFD 方法同時考慮了流體的黏性和旋度，能夠提供更高精度的船舶操縱結果；且與船舶試驗相比，采用CFD 方法對全流場進行數值求解，能夠提供豐富的流場數據。

近年來，國內外基于CFD 方法，采用不同的研究手段進行的操縱運動數值模擬大致可以分為2 種：約束模操縱運動模擬和自航模操縱運動模擬。王慧婷和畢毅[11]利用STAR-CCM+軟件，針對全附體KCS 船模開展了斜航、純艏搖、漂角和艏搖組合這3 種平面運動機構（PMM）試驗數值模擬。Zhang 等[12]以光體ONRT 船模為研究對象開展了斜航拖曳試驗，并利用OpenFOAM 進行數值模擬，給出了可用于分離型建模（MMG）模型的水動力導數。計算機性能的發展和重疊網格技術的應用讓自航模操縱試驗直接數值模擬成為可能。建立船?槳?舵系統數值模型，通過控制螺旋槳旋轉和操舵來實現船舶自航操縱模擬，可以更加精確地預測船舶的操縱運動過程。Sadat-Hosseini等[13]通過采用體積力法和離散螺旋槳對KP458槳進行處理，對KVLCC2 船開展了操縱性試驗數值模擬。Carrica 等[14]采用重疊網格，實現了在淺水工況下對KCS 船模修正型20/5（其中分子為舵角，分母為進行反向操舵時的艏向角，以下同此）Z 形操縱試驗的數值模擬，并進行了網格驗證。王建華等[15]利用自主開發的naoe-FOAM-SJTU 求解器，針對ONRT 船模進行了波浪工況下的回轉操縱試驗模擬。

然而，以上研究都是在一定縮尺比下開展的，試驗中螺旋槳轉速對應于船模自航點，未進行摩擦阻力修正，忽略了尺度效應的影響。考慮到在實船自航方面已經積累了一定的經驗[16-17]，針對實船操縱性試驗的直接模擬已經可以實現，且實尺度計算已被用于研究尺度效應、節能設備（ESD）等方面[18-19]，因此有必要開展實尺度下船舶操縱運動的精確預報，為船舶設計提供一些數據作為參考。本文將基于重疊網格技術，采用STAR-CCM+商業軟件，直接模擬實尺度船?槳?舵相互作用下的自航及10/10 標準Z 形操縱運動，分析實尺度船舶在運動過程中的船舶運動、水動力、流場與渦結構變化。

1 數值方法

1.1 流體控制方程及數值格式

本文船體周圍的流動被認為是三維非定常不可壓縮流，求解的控制方程為RANS 方程：

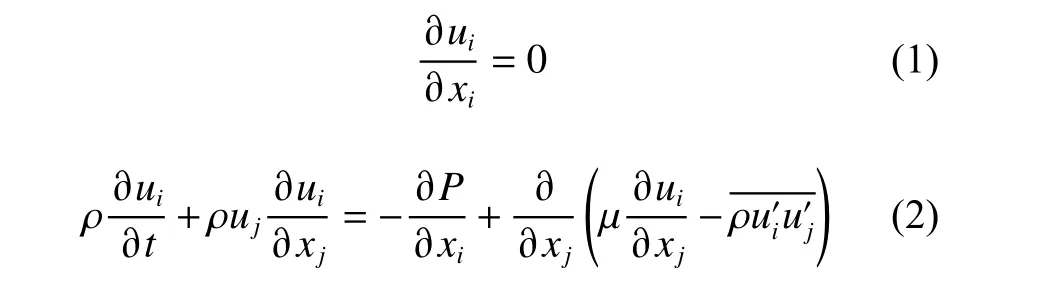
式中：xi和xj為空間坐標分量；ui和uj為空間平均速度分量； ρ，P， μ分別為流體的密度、靜壓力和流體動力黏度；t為時間；?ρu′iu′j為雷諾應力項，需引入湍流模型以使方程封閉。本文引入了兩方程SSTk-ω[20]湍流模型來封閉雷諾應力項，該模型綜合了標準k-ω 模型和k-ε 模型的優點，近壁面選擇Ally+wall treatment 進行處理。船舶自航操縱時產生的自由表面興波采用流體體積（volume of fluid，VOF）法進行界面捕捉，高分辨率界面捕捉（high-resolution interface capturing，HRIC）技術被用來提高自由面的模擬精度。

采用有限體積法（FVM）對整個計算域進行空間離散，采用二階迎風格式離散對流項，用隱式二階精度插值格式離散擴散項，時間項的離散則采用二階歐拉隱式數值格式。方程的壓力?速度耦合求解通過 SIMPLE 算法實現。

1.2 重疊網格技術

重疊網格技術是指將重疊區域的網格通過挖洞、插值的方式嵌套到背景網格中，重疊網格界面存在數據交換。本文中，船?槳?舵系統的自航模擬共有4 套計算網格：1 套背景網格、1 套船體網格、1 套螺旋槳網格、1 套舵網格。重疊網格的分布如圖1 所示。

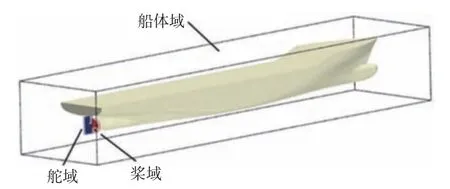
圖1 重疊網格的分布Fig. 1 Distribution of overset grid

1.3 六自由度運動及其坐標系

為了計算船舶運動響應，采用動態流體相互作用（DFBI）方法，以使船舶在六自由度（6-DOFs）中自由運動。DFBI 模型使RANS 求解器能夠計算作用在剛體上的水動力和力矩，并用求解剛體運動的控制方程來確定剛體的新位置。在模擬船舶操縱運動的過程中，螺旋槳和舵作為船體運動的子級物體，可以基于船體六自由度運動進行自身的旋轉運動。

本文中，5 個笛卡爾坐標系被用于船舶操縱運動。其中，大地固定坐標系的原點位于船舶艉垂線與水線面交點處，x軸正向指向船艏，y軸正向指向船體左舷，z軸正向指向船體上方；背景域運動坐標系的原點位置及方向同大地坐標系，隨船舶在x-y平面運動；船體移動坐標系的原點位于船舶重心處，x軸正向由船艉指向船艏，y軸正向由船體左舷指向右舷，z軸正向指向船體下方，且隨船舶六自由度運動；螺旋槳和舵坐標系的位置與船體坐標系相對固定，旋轉軸分別與槳軸和舵桿平行。

2 實尺度船舶自航數值模擬

2.1 計算模型及網格劃分

本文選取帶全附體的KCS 船為計算對象，船體三維模型如圖2 所示，主要的船體及其附體參數如表1 所示。

圖2 KCS 船幾何模型Fig. 2 Geometry model of KCS ship

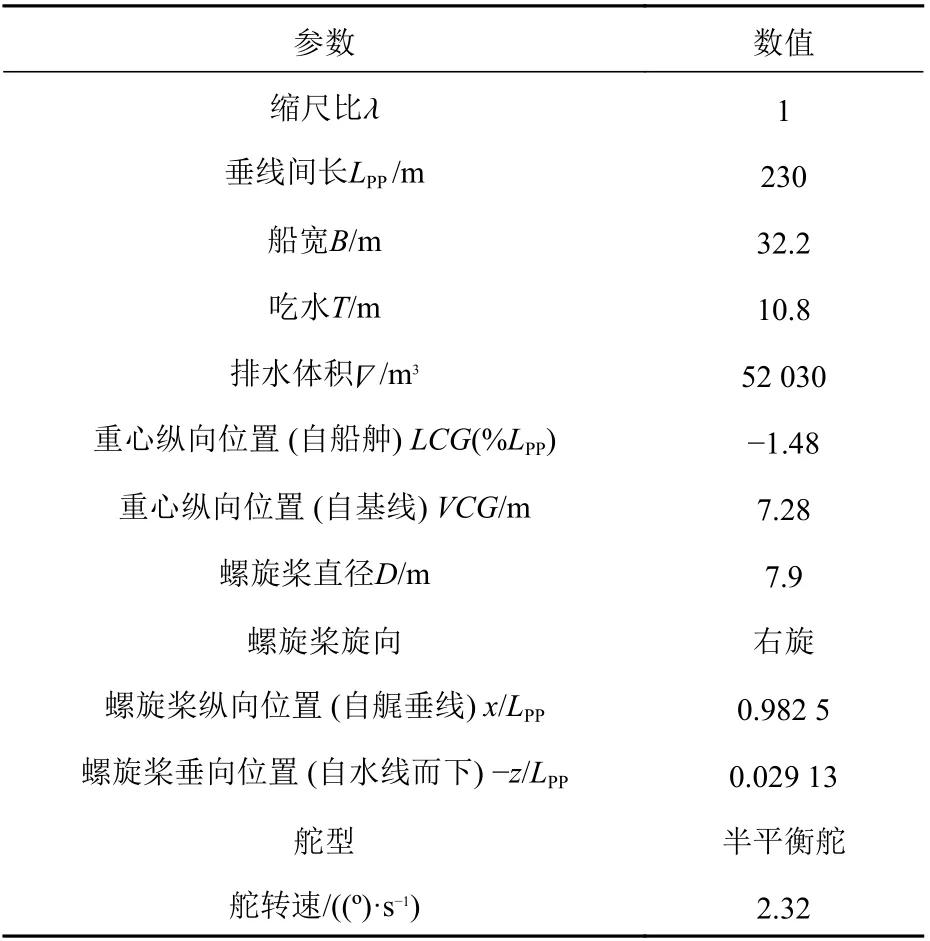
表1 主要的船體及其附體參數Table 1 Main parameters of ship hull and appendage

背景域網格范圍為：?1.5LPP≤x≤2.5LPP，?2LPP≤y≤2LPP，?1LPP≤z≤0.5LPP；船體重疊區域網格范圍：?0.12LPP≤x≤0.1LPP，?0.12LPP≤y≤0.12LPP，?0.1LPP≤z≤0.09LPP。計算域及三維網格分布如圖3 所示。出口為壓力出口邊界，其余邊界條件均為速度入口。

圖3 計算域及三維網格Fig. 3 The computational domain and three-dimensional grid

對于背景域以及船體、舵重疊區域，采用切割體網格進行劃分，槳域網格為多面體網格，重疊域邊界所在位置的2 套網格尺寸保持一致，以減少插值誤差。對船艏、艉軸曲率較大的地方進行局部加密，在艉軸與槳、舵桿與舵面之間的小間隙處放置足夠數量的網格。在自由波面波高方向，劃分10～12 層網格用以捕捉船舶航行所帶來的興波，尾流加密區的網格尺寸則應足夠小，以捕捉槳后渦結構。實船的雷諾數較高，根據推薦，船體表面y+值約為200[21]，實槳的y+接近于30[22]。不同于船模，實尺度船體表面為粗糙壁面，根據文獻[14]，設置等效的砂粒粗糙度高度ε = 32 μm。自航船舶不同區域的網格數量如表2 所示，局部網格分布如圖4 所示。

表2 自航模擬網格分布Table 2 Grid distribution of the self-propulsion simulation

圖4 重疊區域網格分布Fig. 4 Grid distribution of overset domains

2.2 計算工況及結果分析

本文計算工況的設置參照東京2015 船舶CFD研討會上的自航模擬算例。弗勞德數Fr= 0.26（航速U= 12.35 m/s），雷諾數Re= 2.487×109。螺旋槳轉速通過引入PI 控制器進行控制，螺旋槳通過調整轉速來達到船舶指定航速。螺旋槳PI 控制器的公式如下[23]：

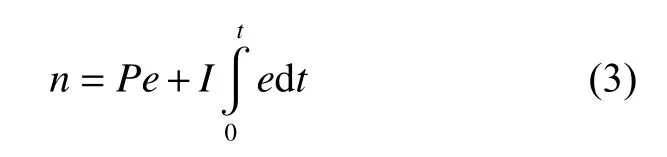
式中：n，dt，t分別為螺旋槳的轉速、單位時間步和旋轉時間長度；P，I分別為比例常數和積分常數，本文設置為P=I= 40；e為目標航速Utarget與實時航速Uship之間的誤差，

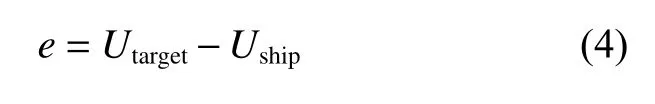
為了節省計算時間，先進行Fr= 0.26 時的深水拖航模擬。通過施加與阻力大小相等、方向相反的強制力，可保證船舶能勻速航行，拖航計算時間步?t= 0.005LPP/U[21]。待自由興波充分發展、阻力穩定之后，將槳域嵌套進拖航計算域中，然后通過PI 控制器調整螺旋槳轉速以達到實船自航點，自航時間步與螺旋槳敞水試驗設置的時間步相同，在每個時間步下，螺旋槳旋轉3o。

深水拖航試驗計算的總阻力系數CT= 2.183×10?3，誤差為?1.7%。螺旋槳敞水計算結果如圖5 所示。圖中，KT為推力系數，KQ為轉矩系數，J為進速系數，η 為敞水效率。

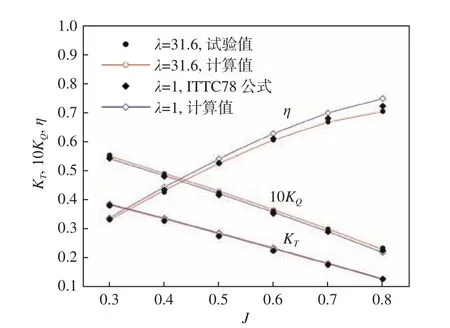
圖5 螺旋槳敞水特性曲線Fig. 5 Open water performance curves of propeller

模型槳推力系數KT和轉矩系數KQ的計算值與試驗值的最大誤差分別為3.14% 和1.35%，實槳推力系數KT和轉矩系數KQ的計算值與ITTC修正值的最大誤差分別為4.19%和?2.90%。由此可以看出，拖航模擬及螺旋槳敞水計算結果與試驗值間吻合較好，驗證了重疊網格技術對實尺度拖航和螺旋槳敞水計算的合理性。

圖6 所示為自航試驗數值模擬過程中螺旋槳轉速n與實船航速U的時歷曲線。表3 為達到目標航速后得到的自航計算結果，并與試驗值進行了對比，相對誤差用百分比表示。作為比較參考，表3 同樣列出了一些CFD 計算結果。由表3可以看出，除轉矩系數KQ的誤差達7.292%以外，其余計算結果的誤差均在2%以內。轉矩系數誤差大是可以預見的，因為水動力系數的試驗值是韓國船舶與海洋工程研究所（KRISO）在模型尺度下得到的。由圖5 以及文獻[24]可知，螺旋槳的水動力系數存在尺度效應，而尺度效應主要影響螺旋槳的轉矩系數，會導致實尺度螺旋槳的轉矩系數減少，推力系數增大。總體而言，基于重疊網格技術能準確進行實尺度自航推進計算。

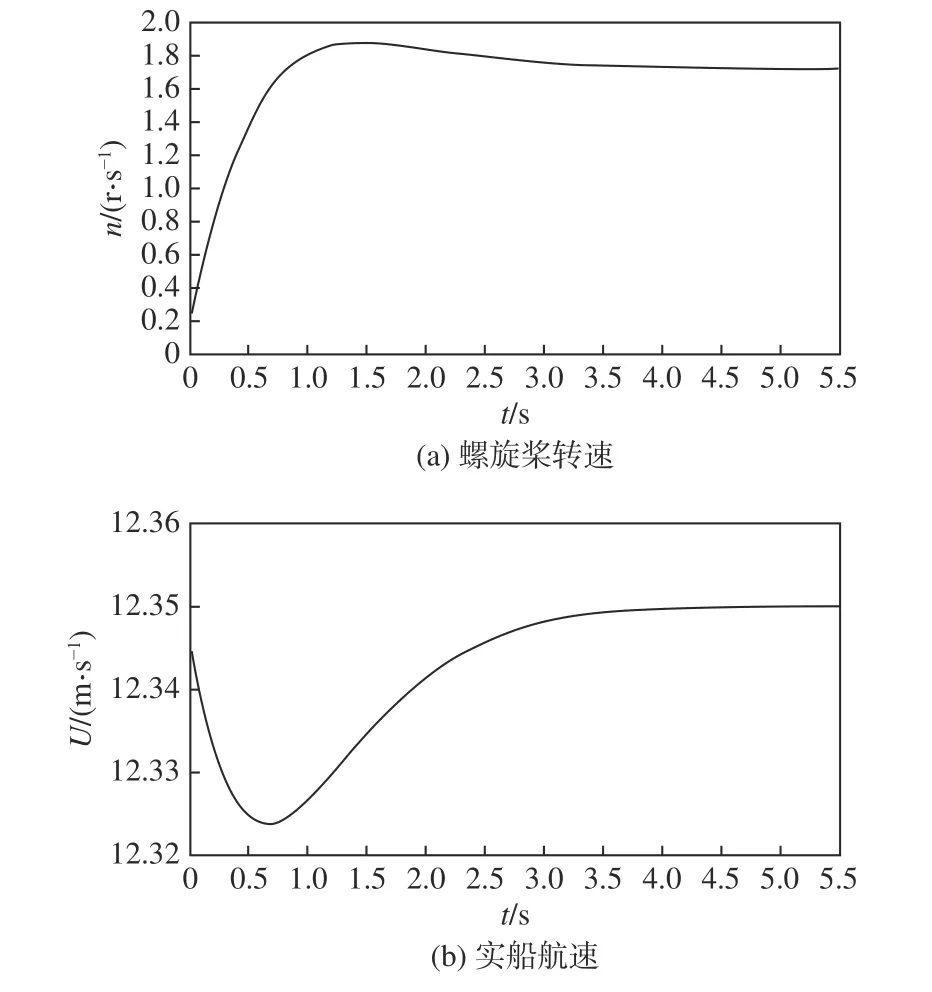
圖6 螺旋槳轉速和實船航速時歷曲線Fig. 6 Time histories of propeller rotation speed and full-scale ship speed

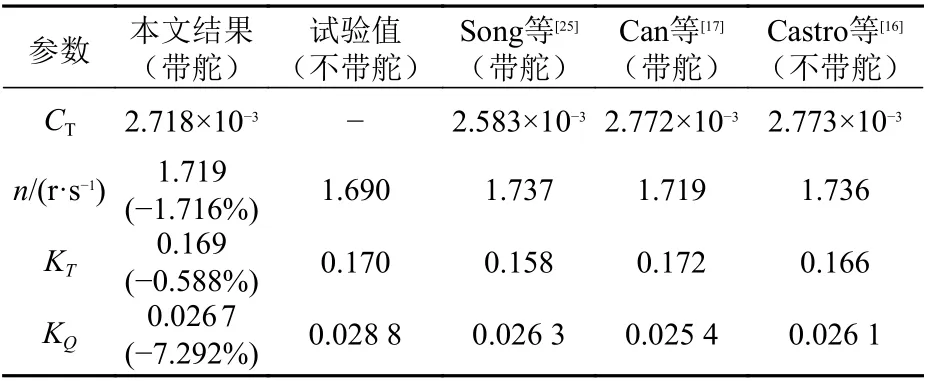
表3 實尺度船舶自航計算結果對比Table 3 Comparison of the self-propulsion results for full-scale ship

3 實尺度船舶Z 形操縱運動數值模擬

舵以指定舵速轉向目標舵角，船體受到響應會向舵角方向轉向，在達到目標艏向角后，操反舵直至達到目標舵角，如此反復，實現船舶的Z 形操縱運動。本文參考SIMMAN 2020 深水10/10標準型Z 形操縱試驗算例，來進行實尺度KCS 船的10/10 標準型Z 形操縱運動數值模擬，采用的計算模型及相關設置與上節相同。在進行Z 形操縱之前，先進行實尺度的自航推進計算，在船舶航行的同時放開垂蕩和縱搖這2 個自由度；待到達實船自航點（Fr= 0.26）后，保持轉速不變，然后放開其余4 個自由度，以2.32 (o)/s 的舵轉速開展10/10 標準型Z 形操舵試驗模擬。

圖7 給出了10/10 Z 形操縱的船舶運動和舵角時歷曲線。同模型試驗一樣，采用CFD 方法只計算了一個Z 形操縱周期。由圖7 可以看出，船舶艏向角速度曲線與漂角曲線形狀相似，但方向相反。在艏向角達到換舵艏向角并開始操反舵時，艏向角速度、漂角、橫搖角、縱搖角以及垂蕩都會出現峰值，此時的船舶運動將最為劇烈。而橫搖角則因船舶本身固有的橫搖周期，會具有更高頻率的橫搖變化。

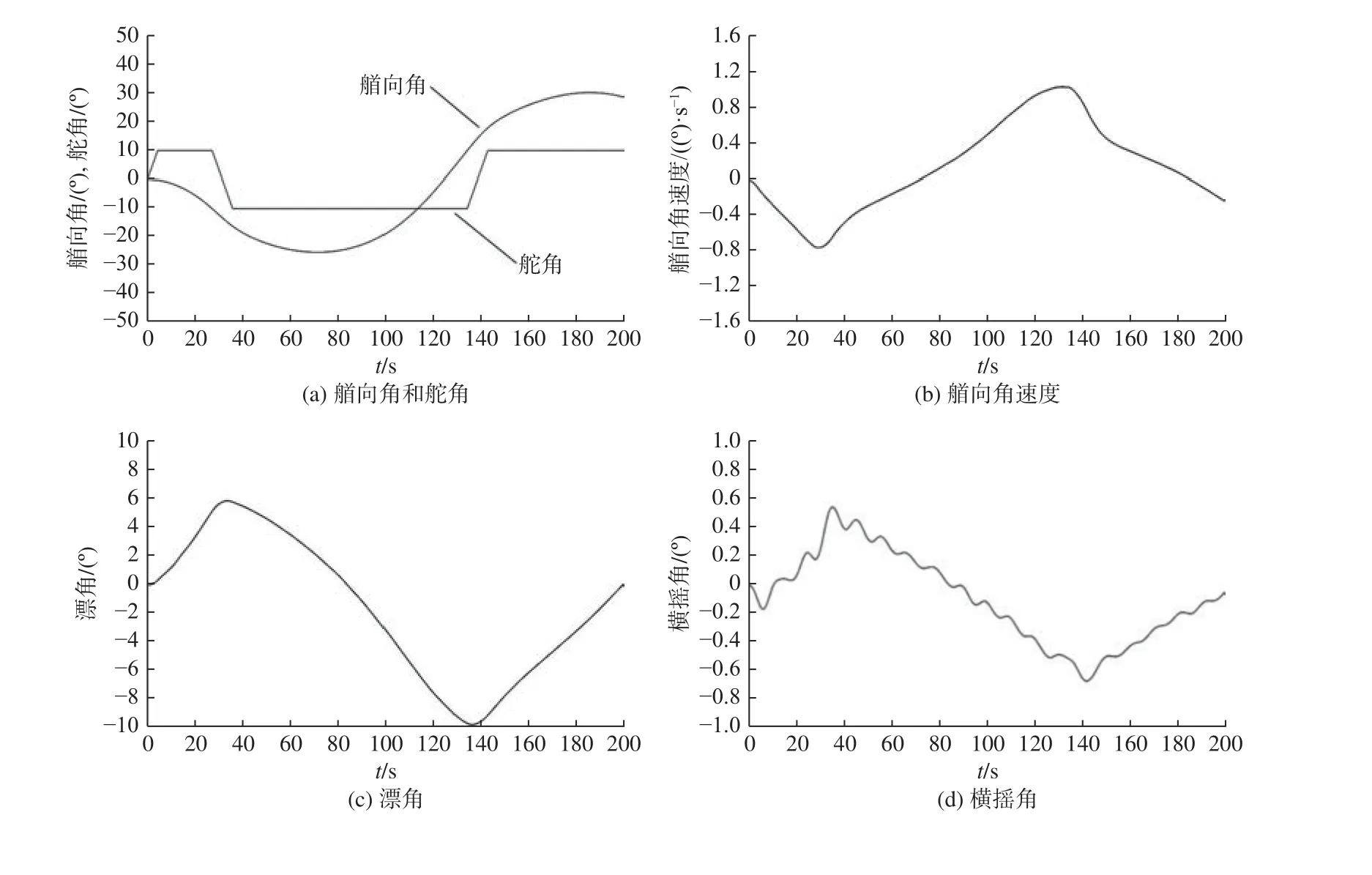
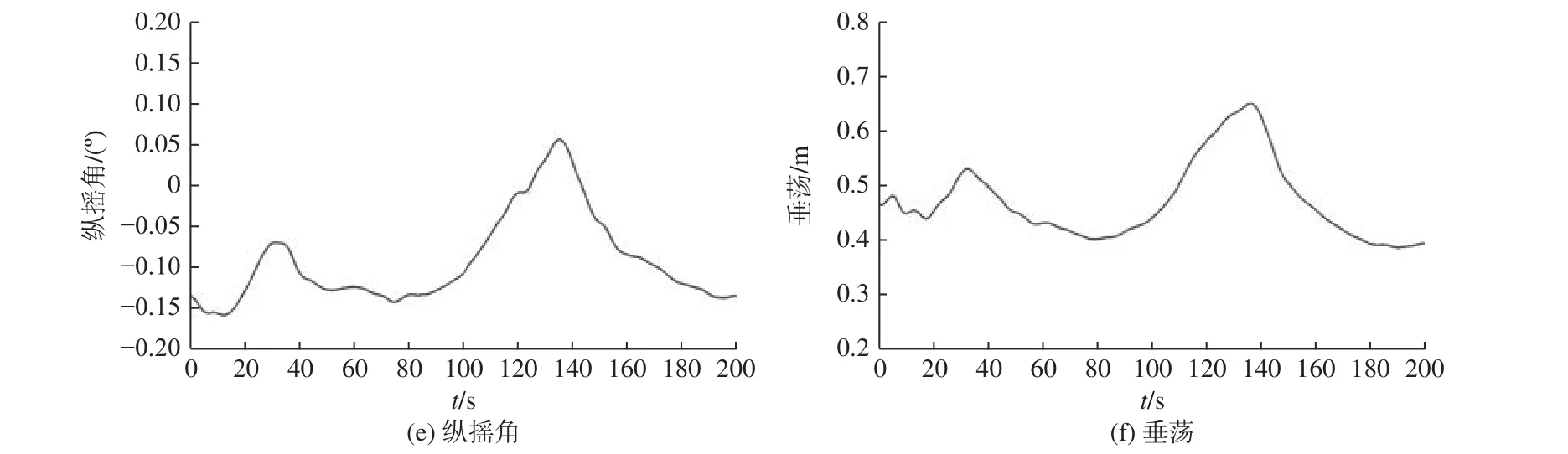
圖7 實船運動及舵角的時歷曲線Fig. 7 Time histories of full-scale ship motion and rudder angle

實尺度KCS 船在10/10 Z 形操縱過程中的最大艏向角、超越角以及最大艏向角速度見表4。

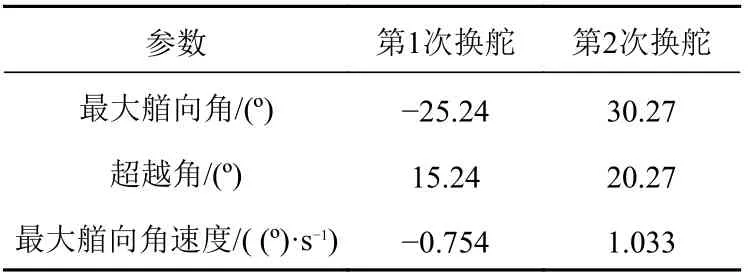
表4 實尺度KCS 船Z 形操縱計算結果Table 4 Calculation results of zigzag maneuver for full-scale KCS ship

圖8 示出了一個10/10 Z 形操縱周期的航速變化曲線。由圖可見，在這一周期內，航速整體呈下降趨勢，且未出現周期性的變化。曲線上較快的降速均發生在兩次操舵執行之后。

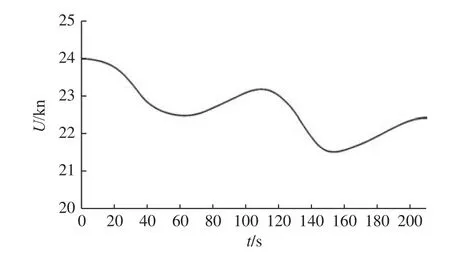
圖8 航速時歷曲線Fig. 8 Time history of ship speed

圖9 所示為10/10 Z 形操縱過程中螺旋槳推力和轉矩時歷曲線。從圖中可以看出，在船舶操縱運動過程中，螺旋槳的推力和轉矩出現了低頻波動，且推力與轉矩的波動情況類似；另外，由局部放大圖可以看出高頻的波動現象，這是由離散螺旋槳在真實旋轉過程中槳葉切割流場所導致。舵的運動會加劇螺旋槳的高頻振動，因此在舵角變化的這一段過程中，船體受到的軸承力會增大，而這對船舶的振動與噪聲不利。在這一個操縱周期內，平均推力的波動范圍為?34.39%～44.74%，平均轉矩的波動范圍為?27.37%～36.97%。在實船操縱過程中，螺旋槳的水動力變化較為明顯。

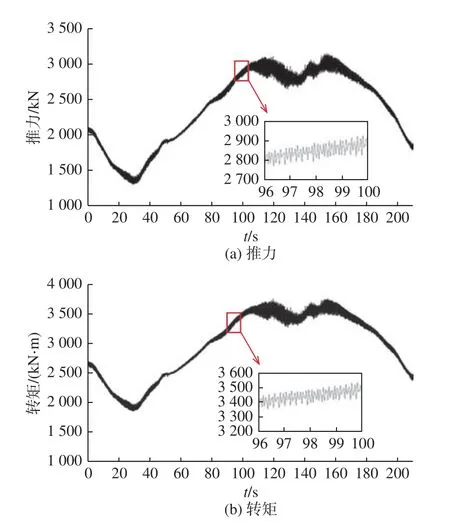
圖9 螺旋槳推力和轉矩時歷曲線Fig. 9 Time histories of propeller thrust and moment

舵阻力和升力的計算結果如圖10 所示。操舵會使來流攻角急劇變化，其中阻力存在2 個低谷，升力則會發生突變。相對于零舵角自航，在船舶操縱過程中，舵阻力較大，最高峰值達350 kN，這也是造成航速下降的主要原因之一。

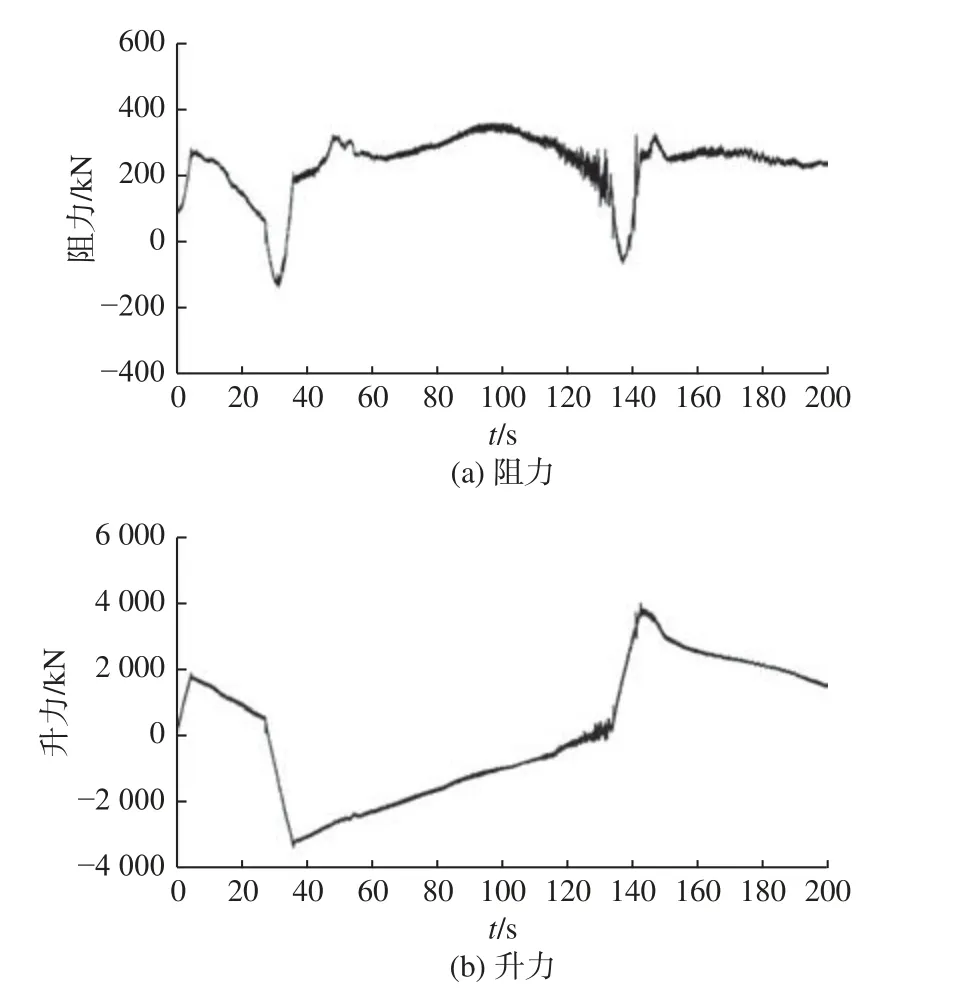
圖10 舵的阻力和升力時歷曲線Fig. 10 Time histories of rudder drag and lift

圖11 示出了不同時刻的自由波面波高（上圖）及船體邊界層軸向速度（下圖），這里波高及軸向速度Vx為無量綱。觀察自由波面的變化可以看出，自航推進的自由波面呈良好的對稱性；在操縱運動過程中，漂角和艏向角的變化導致了波面的非對稱性；且兩側的凱爾文角也產生了變化，迎浪面的凱爾文角較大。由圖11（b）和圖11（c）可以明顯看出，2 個漂角狀態下的凱爾文角并不對稱，最大負向漂角的波形略大，究其原因，可以歸結為在這一操縱周期內，漂角并不呈對稱性變化（圖7）。由圖11 所示沿船長方向的邊界層橫截面軸向速度分布可以看出，隨著漂角的變化，邊界層的速度分布表現為非對稱性，在迎浪面出現了舭渦，且最大負向漂角時刻的舭渦尺度較大；船艉艉軸處伴流因漂角的變化發生了同向偏移，進而改變了螺旋槳的進流迎角。

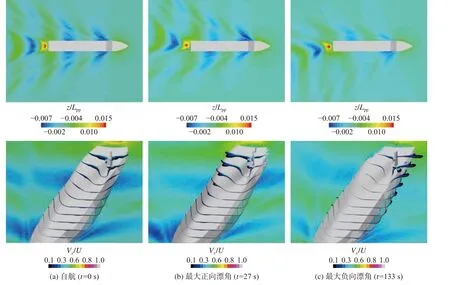
圖11 不同時刻的自由波面及邊界層橫截面Fig. 11 Free wave surface and cross sections showing the boundary layer at different moments

圖12 示出了Q= 2 時不同時刻三維渦結構的軸向速度，Q準則渦量的等值面用無量綱化軸向速度著色，其中深紅色部位代表高速度分布。由圖12（a）可以看出，因為加密區域的存在，螺旋槳整體渦結構能夠被清晰地捕捉到。受舵的干擾，螺旋槳左半部分泄出的梢渦有向上流動的趨勢，右側渦有向下流動的趨勢。槳轂渦受到舵的作用，被分割為兩股，分別在舵的左、右兩側向后發展，并且具有較高的渦強度。在舵的梢部及根部，存在兩股向后發展的渦。總體而言，相比無舵的螺旋槳槳后渦結構，螺旋槳泄渦與舵相互作用會導致更為復雜的渦結構干擾。

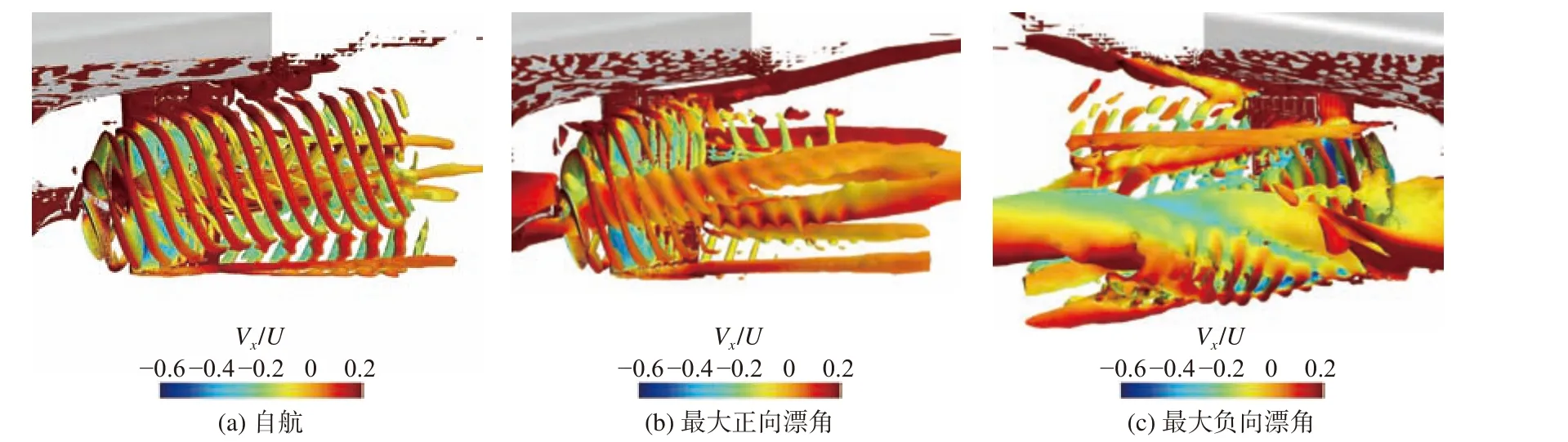
圖12 不同時刻的三維渦結構軸向速度（Q = 2）Fig. 12 Axial velocity of three-dimensional vortical structures at different moments (Q = 2)

由圖12（b）和圖12（c）可以看出，隨著舵角及漂角的改變，螺旋槳泄渦產生了嚴重的偏向，船體底部生成的縱向尾渦使得螺旋槳的整體渦結構更為復雜。圖12（b）示出了最大正向漂角的螺旋槳三維渦結構，此時，舵角偏向左舷10°。從中可以看出，梢渦強度有所減弱，而來自船體的縱向尾渦則穿過槳盤面，與槳的隨邊渦和槳轂發生融合，進而形成強度較高的兩股泄渦并向后方傳遞。圖12（c）示出了最大負向漂角的螺旋槳三維渦結構，此時，舵角偏向右舷10°。與最大正向漂角渦結構不同，梢渦強度有所增大。且由于最大漂角指向船體右舷的幅值相對較大，導致船體縱向尾渦尺度更大，右側部分梢渦與船體縱向尾渦在下方產生了融合，從而形成了一股尺度較大的向后發展的泄渦。顯然，對于因操縱運動而產生的復雜渦系結構問題，需要選擇合適的加密區域，采用精細的網格來捕捉完整的螺旋槳槳后渦流場的演變，這就對實尺度渦流場計算提出了更高的要求。

4 結 語

本文基于重疊網格技術，采用商業軟件STARCCM+，對船?槳?舵一體的實尺度船舶的自航及10/10 標準Z 形操縱運動進行了直接模擬，結果顯示實尺度KCS 船的自航數值計算結果與試驗值吻合良好，表明基于重疊網格技術進行實船自航計算是合理的。

然后，在此基礎上給出了10/10 標準Z 形操縱一個周期內的船舶運動與水動力特性時歷曲線，數值預報了最大艏向角、超越角及最大艏向角速度。計算結果表明，船舶運動在滿足給定的換舵艏向角繼而開始操舵這一過程中，艏向角速度與漂角均會出現峰值，且在此階段船舶運動姿態最為劇烈。由于操縱運動的對象為單槳船，在螺旋槳的右旋運動作用下，船舶操縱運動及船舶水動力均呈現出非對稱性。

最后，根據在不同時刻得到的流場信息，分析了自由面、船體邊界層和渦結構的變化。分析結果表明，在船舶操縱運動過程中，迎浪面的凱爾文角較大，且在舭部出現了舭渦；艉軸處的伴流場因為漂角的改變會產生同向偏移；由于漂角的改變，螺旋槳產生的渦結構相比自航會更加復雜；槳葉梢部的螺旋形梢渦受到干擾，渦強度有所減弱，難以辨識；槳轂泄出的轂渦在與縱向尾渦融合后，渦尺度和強度會有所增大。因此，需要采用更加精細的網格與數值方法來捕捉。

本文針對實船操縱運動進行的直接模擬可以為實船操縱性能評估、船舶數字化設計及操縱手段的選擇提供一定的參考。未來，還可針對實船與船模因雷諾數的差異而產生的尺度效應問題，及其對船舶操縱性能的影響，開展更加深入、細致的研究。