一種新的不常用備件需求預測和庫存優化方法

孔子慶， 劉白楊， 劉 濟

（ 1. 華東理工大學信息科學與工程學院，上海 200237；2. 國家管網集團北方管道有限責任公司壓縮機組維檢修中心，河北廊坊 065000）

由于需求數據的隨機性和非平穩性，不常用備件的需求預測是庫存控制研究領域的一大難題。對于不常用備件的間斷型需求數據，基于時間序列分析的指數平滑法[1]、Croston法[2]、神經網絡[3]等點預測方法精度較低，因此，基于概率統計理論的預測方法受到研究者的青睞。傳統的統計預測方法選擇常見的概率分布函數來描述備件的需求規律，例如Negative exponential分布、Normal分布及Poisson分布等[4]。但是，需求分布函數的選擇缺乏有效的理論依據，而且需求數據常常并不滿足這些常見的概率分布。對此，許多研究者選擇通過一種增廣樣本統計方法——Bootstrap算法來估計需求量的概率分布情況。如Willemain等[5]將Markov模型與Bootstrap法相結合，得到提前期內需求量的概率分布。Aris等[6]對文獻[5]方法與指數平滑法進行了比較，肯定了文獻[5]方法的優越性。但文獻[5]僅考慮需求發生與不發生兩狀態之間的轉移概率，基于此概率預測提前期需求發生次數，預測精度還有提升空間。

另一方面，一些學者將研究重點聚焦于庫存優化上，通過設置訂購點、安全庫存等方法來提高需求預測的容錯性和庫存控制的魯棒性。如Yonit 等[7]通過連續檢查庫存(Q，R) 模型，最大程度地降低庫存總成本。Wang等[8]則通過構建(T，S)模型來應對備件的供應風險。這些庫存優化模型都是建立在需求服從某一已知概率分布的假設上，缺乏合理性。針對間斷型需求預測的難點，另有一些學者將需求預測與庫存優化結合起來。如Ehrenthal等[9]通過研究需求數據中的季節性因素，證明了在庫存管理中考慮非平穩需求可有效降低庫存成本和缺貨成本。劉琴等[10]將需求分布預測與(s，S)模型相結合，構建備件庫存優化模型，但該模型中的需求分布是基于文獻[5]方法得到的，模型的準確性有待提高。

本文提出了一種將需求預測與庫存優化相結合的新方法，采用高斯過程回歸 (Gaussian Process Regression，GPR) 方法對需求發生間隔進行預測，結合Bootstrap算法對需求量序列進行重采樣，預測提前期內需求量的概率分布，基于此預測結果建立庫存總成本最小的優化模型，使用粒子群算法尋優得到最優庫存決策結果。

1 高斯過程回歸方法

不常用備件的庫存決策流程如圖1所示。其中，高斯過程回歸方法用于需求間隔預測。

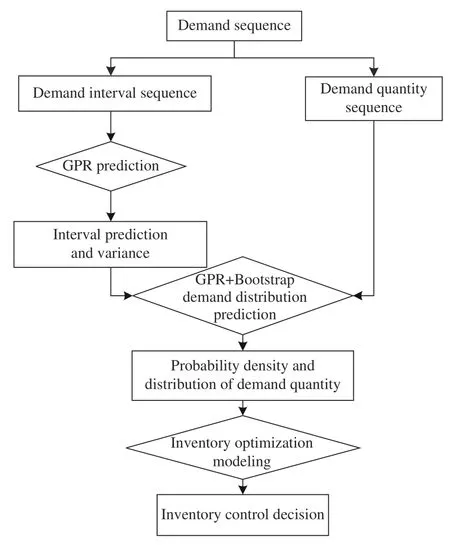
圖1 不常用備件庫存決策流程Fig. 1 Rarely used spare parts inventory decision process

高斯過程（Gaussian Process，GP）是指一個隨機過程，其中任意隨機變量的有限子集均服從聯合高斯分布[11]。

對于一個給定樣本數據集D=(xi，yi)，i=1，2，…，n，其中輸入數據xi∈Rd，為d維輸入量，輸出數據yi∈R。在所給數據集D的有限集合中，f(x1)，…，f(xn)構成一個具有聯合高斯分布的隨機變量集，此時高斯過程的所有統計特性由均值函數m(x)與協方差函數k(xi,xj)構成，即

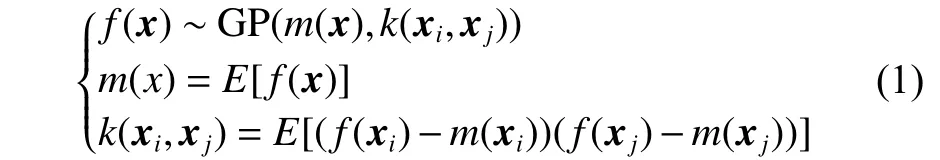
其中：xi，xj∈Rd；f(x)表示均值函數為m(x)、協方差函數為k(xi，xj)的高斯過程函數。

建立一個包含噪聲的高斯過程模型

當m(x)=0時，有限觀測值y的先驗分布為

其中：δij是Kronecker delta函數。

將觀測值y的協方差以矩陣的形式表示：

其中：X=(x1,…,xn)T；C(X，X)表示n×n的協方差矩陣；In表示n×n的單位矩陣；K(X，X)為n×n的對稱正定協方差矩陣，其中的矩陣元素Kij=k(xi，xj)。

給定測試樣本x?,則觀測值y與其預測值y*的聯合先驗分布為

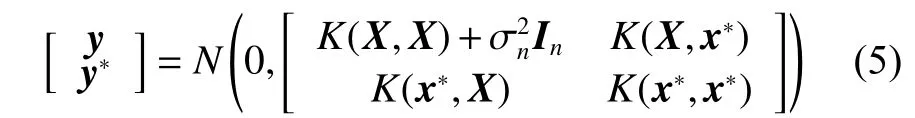
由此可以計算出y*的條件概率分布為

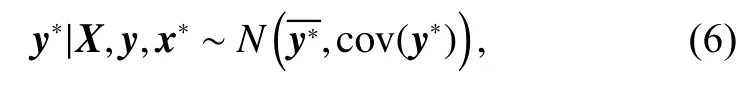
其中

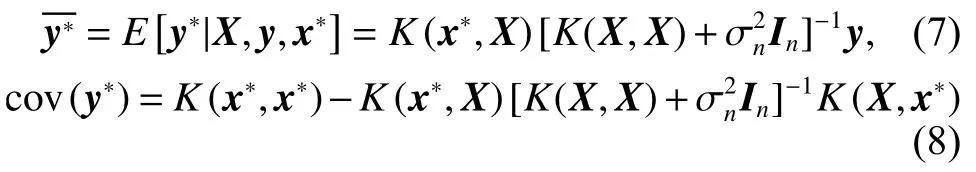
GPR的預測結果與協方差函數(高斯核函數）的選取密切相關。一般選取核函數為平方指數協方差：

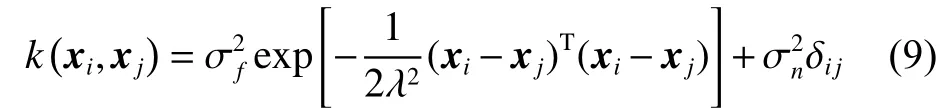
其中：λ為距離尺度；為協方差函數的信號方差。通過極大似然法求取超參數集合 θ={λ,σf,σn} 的最優值。使用共軛梯度法、牛頓法等優化方法求得令似然函數L(θ)極小的超參數最優值。L(θ)的形式如下：

2 基于GPR的需求間隔預測

需求間隔是指相鄰兩次需求發生的時間間隔長度。基于時間序列的需求預測算法大都將需求量和需求間隔分離開各自進行預測[2]，這樣，充滿了許多零值的間斷型原始數據便剝離為兩個連續時間序列?需求量序列和需求間隔序列，可以用各種常規的時間序列回歸和預測方法進行分析。

根據Kolmogorov定理可知，任何一個時間序列都可以看成是由一個非線性機制確定的輸入輸出系統，因此，可以將任何時間序列預測問題當作一個非線性系統回歸問題來解決。需求間隔序列為連續時間序列，具有一定統計規律，可以近似為常見的高斯過程。因此，本文通過GPR進行需求間隔序列的預測。

針對間斷型需求時間序列Z=(z1，z2，···，zn)，可直接抽取得到需求間隔序列G=(g1，g2，···，gt)。其中zi表示第i期的需求量，i=1，2，···，n；gj表示相鄰兩期非零需求的時間間隔，j=1，2，···，t。

首先選取需求間隔序列的預測滑動窗數據gt?β,gt?(β?1)，···，gt，建立下一個需求間隔值gt+1與該輸入序列之間的高斯回歸模型

其中：β為參與預測的數據滑動窗參數，則β+1為滑動窗大小，即預測維數。恰當地選取預測維數是數據預測方法的關鍵。

然后，以需求間隔樣本序列G=(g1，g2，···，gt)作為學習樣本，訓練高斯過程回歸模型，獲得模型超參數最優解，便可以獲得需求間隔預測值t+1及其方差。

3 基于GPR和Bootstrap的需求概率分布預測

Bootstrap算法是一種增廣樣本統計推斷技術，其基本思想是在原始數據集中進行多次有放回的隨機抽樣，每次抽取N個數據，構成觀測樣本，然后根據觀測樣本生成反映原始數據的抽樣分布。Williamain等[5]根據需求發生與不發生的歷史轉移概率，對整個需求數據進行抽樣并放回，相較于前人的工作有較大的提升，但是對歷史數據的挖掘并不充分，其后相應的改進研究非常稀少[10]。

本文提出了一種新的GPR與Bootstrap結合的需求概率預測方法，其基本思想是：利用GPR循環預測需求發生間隔均值及其方差，由此進行隨機抽樣，推斷提前期內需求發生的次數。基于提前期需求次數，采用Bootstrap算法對歷史需求量序列進行重采樣，獲得多組提前期需求量預測序列，根據這些預測序列便可估計提前期內需求量的概率密度和累積分布。具體步驟如下：

(1)假定提前期為L，初始化需求間隔預測序列M=[]，令i，j=0。

(2)生成預測滑動窗(gt?(β?i)，gt?(β?1?i)，···，gt+i)，通過GPR方法預測需求間隔分布N(t+i+1,t+i+12)。

(3)對需求間隔分布進行隨機抽樣，獲得下一時刻需求間隔預測值rj，將rj存入需求間隔序列M中，此時M=(r0，r1，…，rj)。判斷預測需求間隔之和是否大于提前期L，若r0+r1+…+rj>L，則將rj從序列M中剔除，并跳轉到步驟(4)。若r0+r1+…+rj＜L，則令i=i+1，j=j+1，gt+i=rj，跳轉到步驟（2）。

(5)重復步驟（1）～（4）共m次，得到m組DL，由其擬合得到DL的概率密度函數f(DL)和累積概率分布函數F(DL)。

具體算法流程如圖2所示。

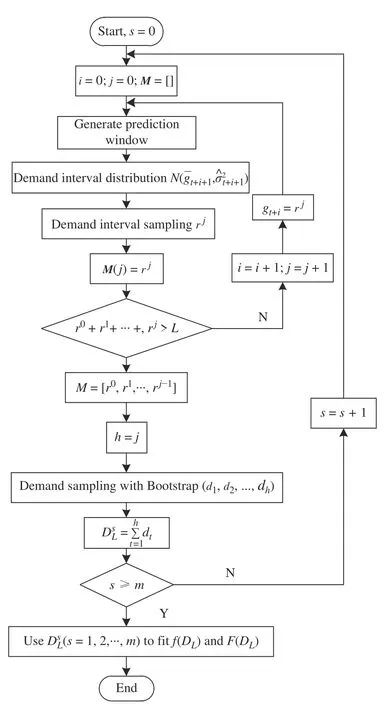
圖2 需求量概率分布預測流程圖Fig. 2 Flow chart of probabilistic distribution forecast

4 基于需求概率分布的隨機庫存優化建模

由于間斷型需求數據的隨機性，任何一種基于時間點預測的方法都難以保證其準確性，因此本文避開需求量時間序列預測的難題，從庫存控制決策的角度出發，尋求提前期內需求量的統計概率[12]，并以此為條件，從統計學的一般意義上來建立庫存成本優化模型，讓提前期需求量的累積概率作為庫存成本控制的一個約束條件，以此獲得有效的庫存決策。

以連續檢查庫存的定點訂購策略(Q，R)為例[7]，定量化隨機性需求所帶來的缺貨損失，建立缺貨不補情況下的庫存總成本優化模型。假定提前期L不變、備件到貨入庫時間很短、備件的單次訂購費A、儲存費率h和缺貨費率s基本不變。基于上述條件，定義DL為提前期內需求量(隨機變量）；f(DL)為提前期需求量的概率密度函數；F(DL)為提前期需求量的累積概率分布函數；R為訂購點；Q為單次訂購量；p為備件的單價；h為單位時間單位價值的儲存費率（%）；s為單位價值備件缺貨一次的缺貨費率(%)。

假定在一個訂購周期ti內，庫存的總成本由儲存成本、訂購成本、缺貨成本構成。

(1)訂購成本CO

一般考慮一次訂購所產生的物流、運輸、人員、稅務等費用基本固定，即不考慮訂購費因訂購量而打折促銷的因素。假設單次訂購發生的訂購成本為常數。

(2)缺貨成本CL

若單位價值的備件一次缺貨造成的損失成本為ps，則缺貨總成本為

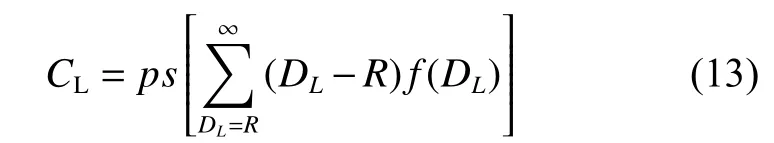
(3)儲存成本CS

CS為備件儲存在倉庫中所產生的管理費、場地費等，與庫存量及其儲存時間有關。若發生缺貨，則平均庫存量的計算應排除缺貨量，庫存時間也發生相應變化[13]。訂貨周期ti內的平均儲存成本為

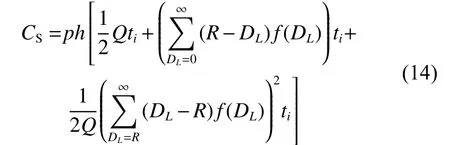
這樣，一個訂購周期ti內總成本為Ctotal(ti)為

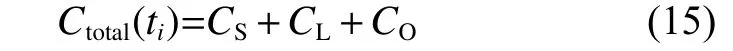
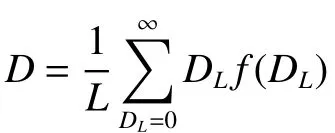
將式(15)等式兩邊同時除以ti，可以得到單位時間內總庫存成本為C，因此，以單位時間總庫存成本C最小為控制目標的優化問題描述為

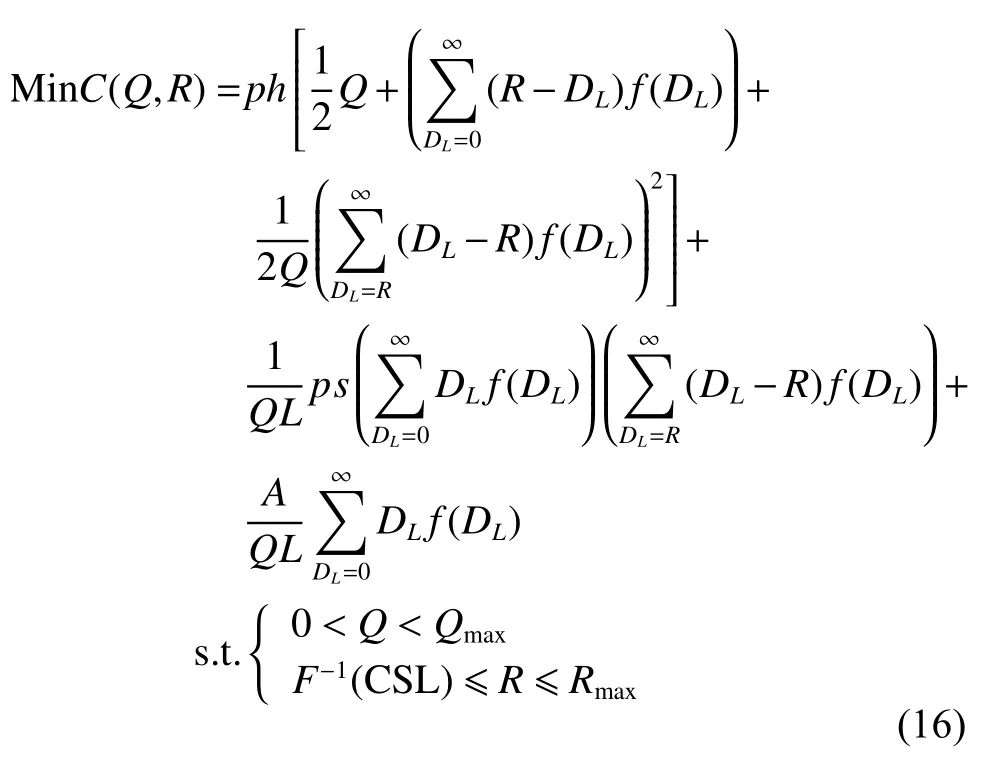
其中：CSL為客戶要求的備件服務水平，代表備件庫存滿足需求的最低概率[14]；F?1表示F(DL)的反函數；Qmax、Rmax分別表示訂購量和訂購點的優化邊界值。

庫存優化模型的主要思想是：在決策變量Q和R的可行解空間(約束條件s.t.給出)，尋找令由訂購成本CO、儲存成本CS、缺貨成本CL之和構成的庫存總成本最小的最優解 (Q*,R*)，該最優解代表了最優訂購點和最優訂購批量。

5 實例分析應用

針對不常用備件的間斷型需求數據，本文提出了一種基于GPR和Bootstrap的需求概率預測方法，并以此為條件來建立隨機庫存優化模型，以提高庫存控制決策的準確性和魯棒性。借鑒文獻[15]的核電設備備件以及文獻[16]的動車組齒輪箱歷史需求數據，對本文算法進行比較驗證。以文獻[15]中核電設備的備件需求數據為例，初始化提前期L為5個月，其需求數據以月為單位進行統計，共有132條數據，其中需求量為0的數據共91條，以第一次發生需求為起點進行統計，平均需求間隔長度為3.075個月，需求量均值為0.47件，標準差為0.604件。

5.1 需求間隔預測實例驗證

從第一次發生需求開始計算需求間隔，將需求序列Z轉換為需求間隔序列G=(1, 6, 5, 3, 1, 2, 1, 1, 1,18, 3, 5, 2, 2, 2, 1, 4, 2, 3, 2, 3, 1, 1, 1, 12, 3, 3, 2, 4, 2, 4,2, 2, 2, 3, 3, 1, 2, 4, 3)。將前37條數據作為訓練數據，第38、39、40條數據作為測試數據，采用本文提出的需求間隔預測算法，得到需求間隔的預測結果如圖3所示。其中超參數集合 θ 的優化值為λ=0.112,σf=1.156，σn=1.162。

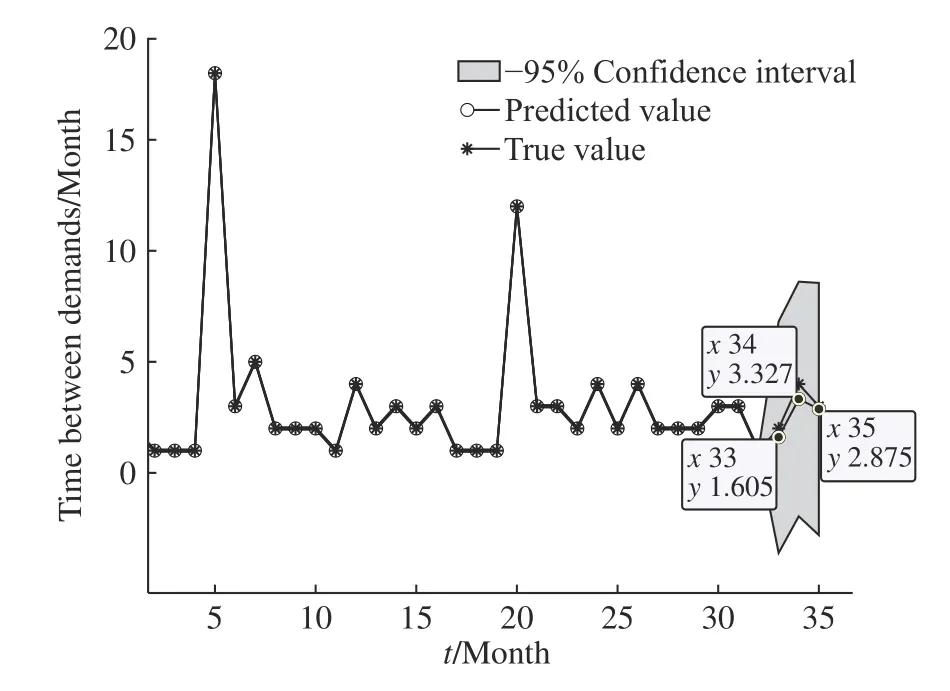
圖3 基于GPR的備件需求間隔預測結果Fig. 3 Spare parts demand interval prediction results based on GPR

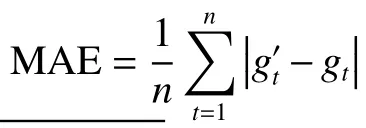
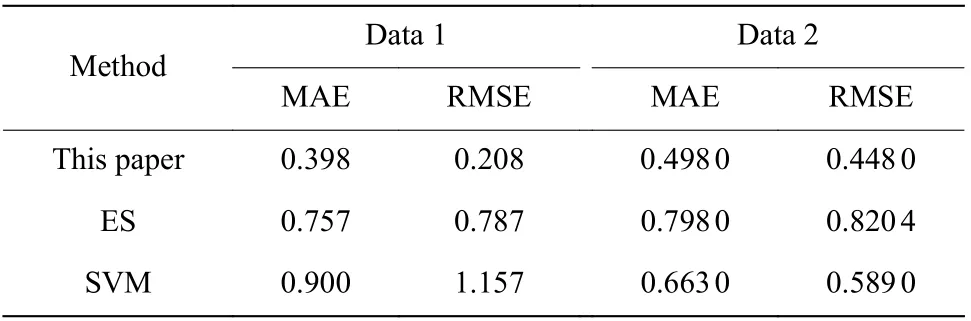
表1 本文方法與其他算法的比較Table 1 Comparison of the proposed method and other algorithms

從表1可以看出，本文方法的平均絕對誤差及均方根誤差均在0.5以下，預測誤差小于ES與SVM，預測效果較好。高斯過程回歸在進行需求間隔預測的同時，還給出了預測值的置信區間（方差），可提高后續Bootstrap抽樣的可靠性，降低預測誤差帶來的影響。

5.2 需求量概率分布預測實例驗證

將GPR與Bootstrap相結合，預測備件在提前期內的需求量概率分布。仍然使用文獻[15]的備件需求數據，根據其需求序列Z的前123個月數據，可得到未來提前期內需求量的概率分布及累積分布。將本文方法與文獻[10]中基于Markov與Bootstrap的方法進行對比，需求量概率分布的對比如圖4所示，累積分布的對比如圖5所示。假定備件服務水平要求為90%以上，則提前期內需求量累積概率達到90%的點設置為安全庫存量。分別設置提前期L=5、8、11，對本文方法與文獻[10]方法的預測結果進行對比，結果如表2所示，其中，置信區間表示概率為95%以內的需求量范圍。

圖4 提前期內需求量概率直方圖Fig. 4 Probability histogram of quantity demanded in lead period

圖5 提前期內需求量累積分布直方圖Fig. 5 Histogram of cumulative distribution of demand in lead period

表2 兩種方法的評估結果Table 2 Evaluation results of two methods

從實驗結果可以看到，不同提前期設置下，需求量真實值均落在兩種方法的95%置信區間內，但本文方法的置信區間比文獻[10]的置信區間更窄，精度更高。并且，安全庫存量比文獻[10]方法得到的更小，可顯著降低備件的庫存總費用。

5.3 隨機庫存決策實例驗證

采用GPR與Bootstrap方法獲得提前期內需求量概率函數f(DL)和F(DL)，由此建立隨機庫存最優化模型式(16)，求解得到最優決策變量作為庫存決策依據。依舊采用文獻[15]中核電設備備件的需求數據，備件單價為23 881元，儲存費率設置為1.5%/a。單次訂購的固定費用設置A=94元，缺貨損失費率s=120%/次。服務水平CSL=90%，即須保證提前期內備件需求得到滿足的概率至少為90%。邊界值Rmax與Qmax均設置為50件。

粒子群算法作為一種啟發式算法，具有操作簡單、尋優速度快的特點[18]，因此本文采用粒子群算法求解優化模型式(16)。在種群大小為100，最大迭代次數為200，慣性權重為0.6，自我學習因子為0.5，群體學習因子為0.5條件下，得到最優尋優結果為Q*=5，R*=4。庫存總成本的迭代收斂過程如圖6所示，可以看出，按照所求得的決策量進行庫存控制，可使庫存總成本最小，有效地控制了庫存總費用。

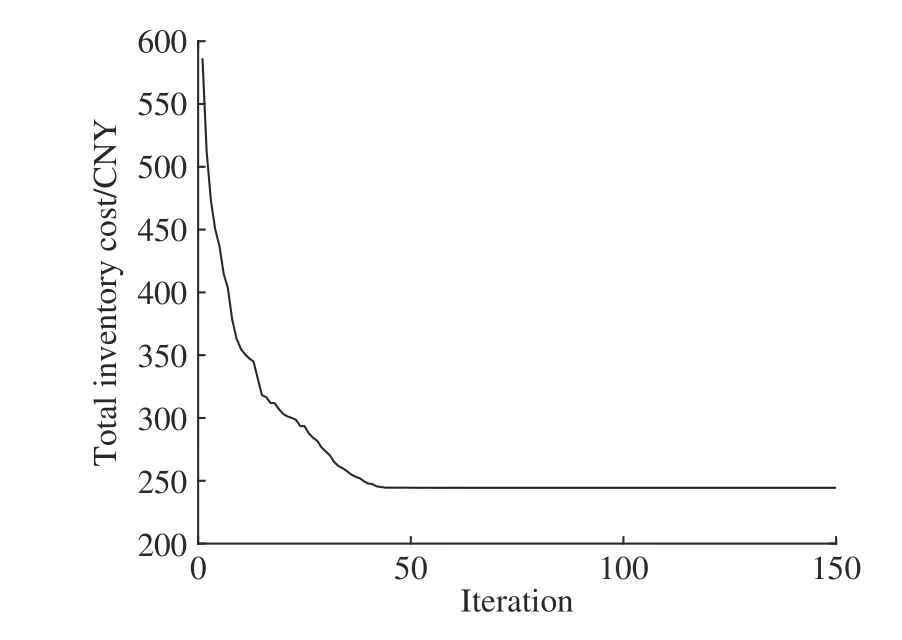
圖6 月最小總成本優化過程圖Fig. 6 Optimization process diagram of minimum total monthly cost

為了檢驗模型求解的庫存決策數據能否滿足實際需求，對歷史需求序列Z采用滑動窗的形式統計該備件提前期內需求量的大小以及發生頻次，窗口大小根據提前期設定為5，每次滑動步數為1，統計信息如表3所示。

從表3可以得到，提前期內需求量最大值為9，最小值為0，其中需求量小于或等于最優訂購點R*=4的累積概率為91.41%，服務水平達到90%以上，滿足模型預設的服務水平要求。

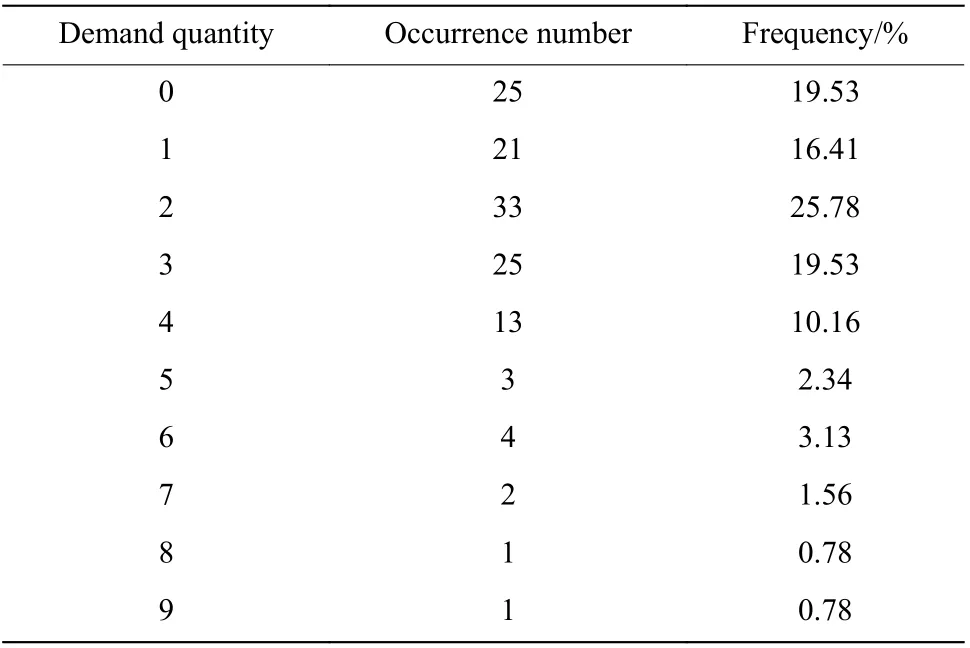
表3 歷史需求量統計信息Table 3 Historical demand statistics

6 結束語

針對不常用備件需求不穩定、波動性強的特點，本文提出了一種需求概率預測和庫存優化結合的新方法，以提高庫存決策的準確性和魯棒性。首先采用GPR預測需求發生間隔，接著結合Bootstrap進行需求概率分布預測，最后以此為條件建立隨機庫存優化模型并求解。實際備件的需求數據數值分析結果表明：基于GPR的需求間隔預測精度相比于指數平滑法、SVM算法都有一定的提高，同時還獲得了預測值的置信區間信息；GPR與Bootstrap結合的需求概率分布預測結果比文獻[10]的置信區間更窄，精度更高，預測結果下的庫存總費用相比顯著減小；基于上述預測結果所建立的庫存優化模型，在保證服務水平的前提下，庫存總成本收斂至最小值，且最優決策變量數值完全符合歷史需求統計結果。