欠膨脹超聲速沖擊射流的大渦模擬

鄭楓弋， 賴煥新

（ 華東理工大學機械與動力工程學院，上海 200237）

超聲速沖擊射流往往伴隨著強烈的傳熱傳質現象，可以提供較大的沖擊力，廣泛應用于航空航天等諸多領域[1]。在垂直起降飛行器（STOVL）上，可以利用機身底部的噴管噴射的高速氣體對地面的沖擊來獲得飛行器所需要的向上推力，從而實現垂直起降和懸停等動作。超聲速沖擊射流的流場結構復雜，激波、剪切層與邊界層存在強烈的干涉，其湍流結構是相關應用中流體動力學的關鍵。

根據Mitchell 等[2]的可視化研究，可以簡述欠膨脹超聲速沖擊射流的流場結構，射流噴出后在中心線附近形成一道激波，通常被稱為馬赫盤，馬赫盤周圍有斜激波。在馬赫盤后的亞音速流與斜激波后的超音速流之間會形成剪切層。在馬赫盤后損失的總壓大于通過斜激波的流動損失的總壓，這導致了在平板中心的壓力低于外側，從而形成一個再循環區。在再循環區和馬赫盤后的氣流之間形成一個接觸面。通過馬赫盤的流體進入剪切層，遠離射流的軸線。斜激波與射流邊界的交點處出現扇形膨脹波，它經剪切層反射，形成環形的壓縮波。這是欠膨脹超聲速沖擊射流可視化得到的平均流場主要特征。

關于噪聲方面，超聲速沖擊射流會產生強烈的離散頻率噪聲，這種噪聲被稱為沖擊單音，其幅值通常高于沖擊射流中其他噪聲，而成為沖擊射流噪聲的主體。Marsh[3]于1961年首先報道了射流沖擊平板產生的離散頻率噪聲。Wanger[4]發展了沖擊射流的不穩定性模型，Neuwerth[5]考慮到噴嘴處產生下行壓力波動，對不穩定性模型進行了改進。Tam等[6]基于中性穩定波在噴流內部主要向上游運動的特點，發展了描述射流沖擊平板的理論模型。Ho等[7]猜測離散頻率的沖擊單音與流場中的反饋環有關，是由平板附近的大尺度擬序結構導致。影響沖擊射流流場結構的主要參數有噴管總壓與環境壓力之比（Nozzle Pressure Ratio，NPR）、噴口到沖擊平板的距離以及沖擊平板的大小。Alvi等[8]在實驗中通過粒子圖像測速技術（Particle Image Velocimetry ，PIV）得到了流場中的速度分布，并測試了沖擊平板上的壓力分布，發現壓力脈動的主頻與沖擊單音的頻率相同。Powell[9]指出，沖擊單音是受噴嘴與壁面之間的反饋環控制。然而，由于流場中存在震蕩，并且流-聲關系十分復雜，這種反饋控制噪聲的機理仍然不清晰。

本文參考Henderson等[10]的實驗工況與劉海等[11-12]的數值模擬，對欠膨脹沖擊射流進行數值模擬分析，著重研究噴嘴到壁面的反饋機制，考察湍流場中大尺度擬序結構的產生和發展演化過程以及沖擊射流中的周期性現象。

1 計算對象與模型

欠膨脹沖擊射流的大渦模擬（LES）使用經過Favre濾波后的Navier-Stokes方程作為控制方程。為使方程中的亞網格應力項封閉，本文使用了WALE亞網格模型[13]，其亞網格黏度被模化為：

式中：Ls=min(κd,CwV1/3) ；κ為von Kármán常數；d為網格點到壁面的距離；Cw=0.325，為WALE常數；V為控制體的體積。

本文計算參考Henderson的試驗工況，其中收縮噴嘴的出口直徑Dj=25.4 mm，噴口距壁面的高度與噴口直徑之比為h/Dj=2.08，來流總壓與環境壓強的比值ptotal/p0=4.03 ，其完全膨脹馬赫數為1.55，噴管外廓錐角為30°，唇厚度為1.27 mm。該工況對應的完全膨脹馬赫數為1.55。計算域的設置如圖1所示。計算網格數為228萬，在沖擊平板上壁面量綱為一距離y+＜5。對于噴管入口給定總壓邊界條件，對于遠場出口給定無反射邊界條件，沖擊壁面和噴嘴壁面使用絕熱無滑移邊界條件。

圖1 計算域設置Fig. 1 Computational domain

使用Fluent UDF在噴口前Dj處添加周向多模態渦環擾動，以觸發流動轉捩[14-15]。

計算中使用AUSM（Advection Upstream Splitting Method）通量分裂，空間上使用3階MUSCL（Monotone Upstream-Centered Schemes for Conservation Laws）格式，時間上使用2階精度隱式格式。初場由RANS Realizablek-ε湍流模型計算得出。大渦模擬的時間步長?t1=1×10?6s ，可保證全場庫朗數CFL=u＜1，Δx為網格間距。經過時長為400Dj/Uj的發展，認為已經排除了初始流場的影響，開始進行變量的采樣統計。采樣間隔為Δt2=5×10?6s，采樣時間持續5×10?3s。

圖2 不同渦環擾動計算結果對比Fig. 2 Comparison of calculation results by different vortex ring perturbations

2 結果與分析

2.1 時均流場

為驗證網格無關性，本文分別對網格數為124萬（Coarse），228萬（Mid），342萬（Fine）的3組網格進行雷諾時均模擬。圖3示出了各組網格中心線上壓力分布，從計算結果中可以看出，在網格數228萬與342萬的算例中，計算結果在峰值處的偏差3.8%，可滿足網格無關性的要求。

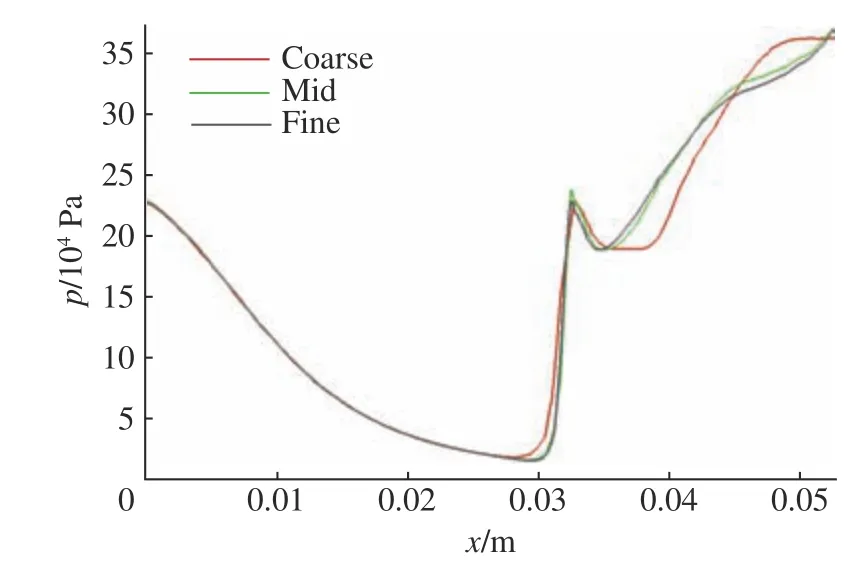
圖3 各組網格中心線上壓力分布Fig. 3 Pressure distribution on centerline of each mesh

圖4 中心線上物理量分布與實驗對比Fig. 4 Comparison of the value on centerline with experiment

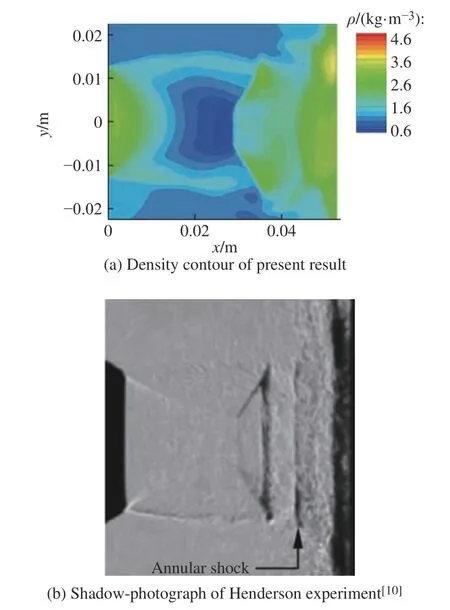
圖5 沖擊射流激波的比較Fig. 5 Comparison of the shock between the calculation and experiment in impinging jet

圖6示出了沖擊區域時均速度場計算與Henderson實驗的比較，圖6(a)是本文計算的速度云圖，可以看到在噴口與激波之間的膨脹區域中，流速不斷增大，并且在激波與壁面間存在低速的再循環區。這種趨勢與圖6(b)中Henderson實驗得到的時均速度場基本一致。說明本文的模擬結果可以有效地模擬超聲速沖擊射流的流場。

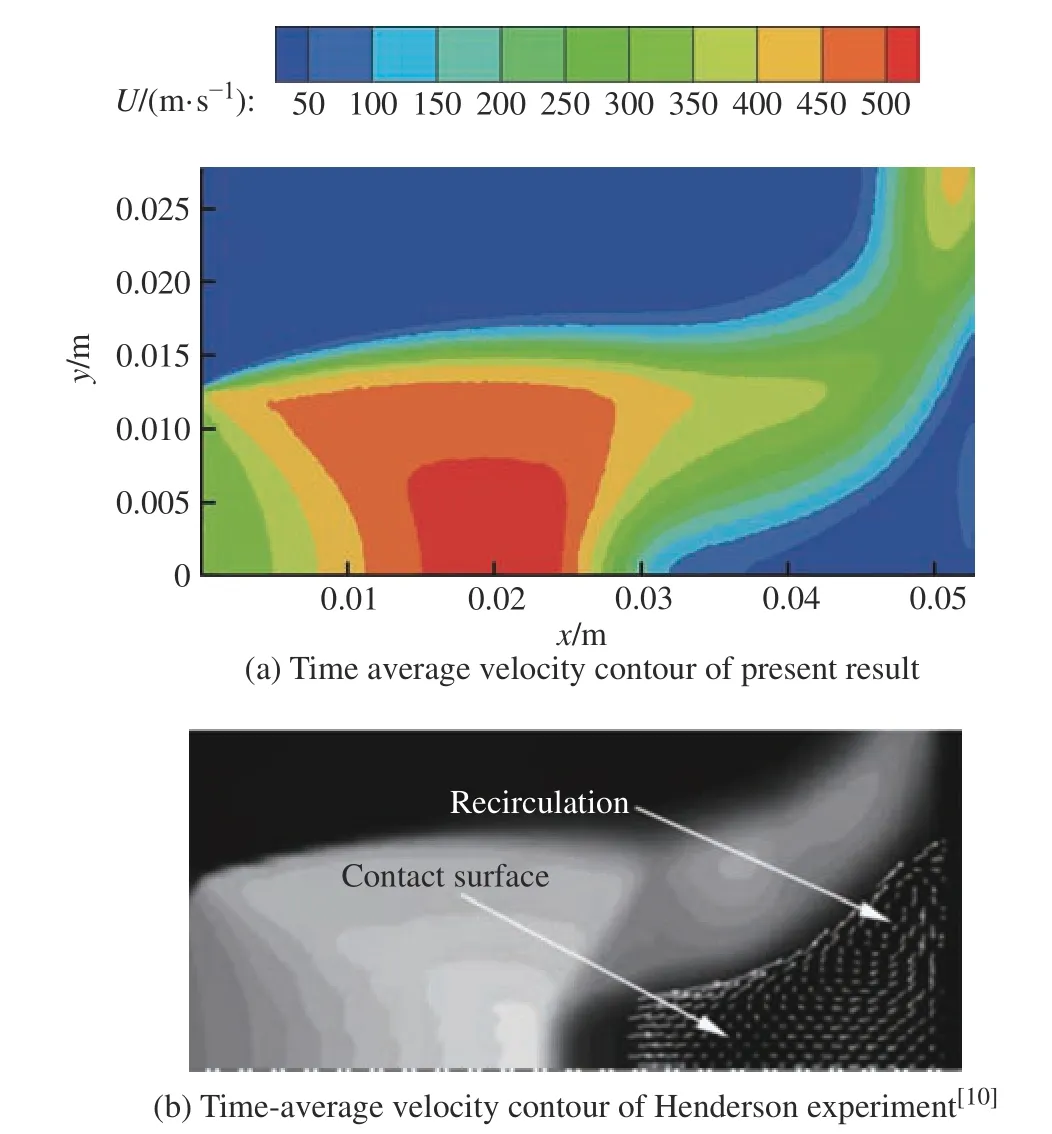
圖6 沖擊射流時均速度計算與實驗的比較Fig. 6 Comparison of average velocity between the calculation and experiment in impinging jet

2.2 瞬態結果與反饋機制

圖7示出了軸截面瞬時合速度分布，各幅圖是等時間間隔的，展示了1個完整的流場震蕩周期(T=2×10-4s)內流場的變化，可以看到流場中激波的位置與強弱存在周期性。圖7(a)和7(b)反映了波系沿軸向向下游運動的過程。在馬赫盤與斜激波向下游運動的過程中，環形激波隨之生成并沿軸向向下游發展，進入壁面射流區。在激波下行過程中，噴口噴出的欠膨脹氣體有了更充分的空間進行膨脹，可以達到更高的速度，這導致了穿過馬赫盤與斜激波的流體速度差增大，使得剪切作用增強，再循環區的影響范圍增大。當再循環區向下游運動時，剪切層和斜激波后的超聲速流動也發生畸變，斜激波后的環形激波隨再循環區向下游運動而消失，其環形激波生成和消失的周期與馬赫盤的震蕩周期相同。圖7(c)和圖7(d)示出了馬赫盤向上游運動的過程中，斜激波隨馬赫盤向上游擺動，在斜激波后方的流體速度差減小，再循環區也變小。在外剪切層與壁面射流的交界處（近壁面處y=0.8Dj）的位置產生渦結構，并有波向上游傳播。

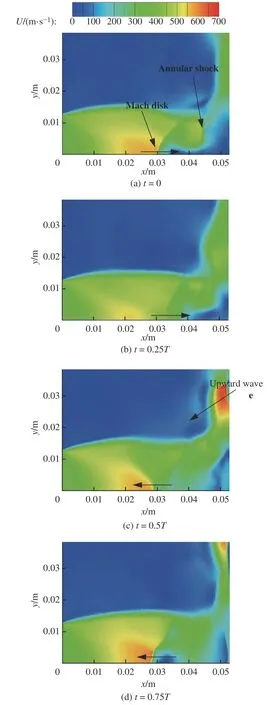
圖7 一個流動震蕩周期內的瞬態速度分布（Δt/T=0.25）Fig. 7 Transient velocity distribution during a flow oscillation period (Δt/T=0.25)

Q判據被廣泛用于渦的辨識，其定義式為

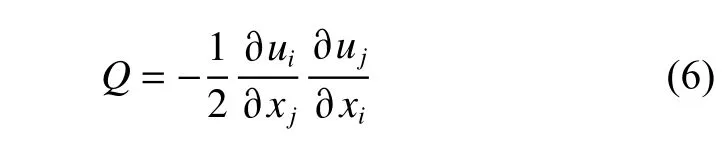
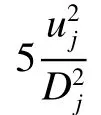
圖8 瞬態流場的Q判據等值面Fig. 8 Iso-surface of Q-criterion in unsteady flow field

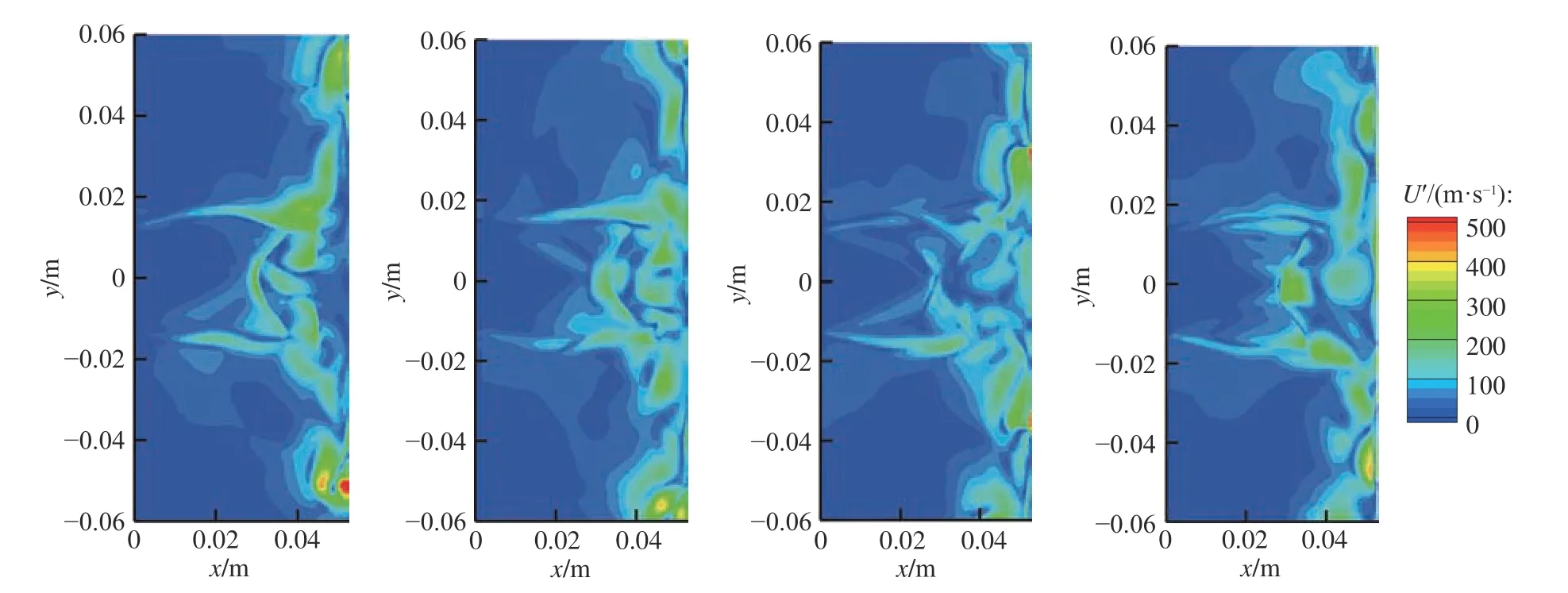
圖9 一個流動震蕩周期內的瞬態速度脈動分布Fig. 9 Transient velocity fluctuation distribution during a flow oscillation period

速度散度 ?·U為連續性方程中的一項，可以反映流場中的膨脹與壓縮現象，也可以描述聲波的傳播，圖10示出了一個流動震蕩周期內的瞬態速度散度分布。可以看出，射流一經流出噴口，就發生高強度的膨脹，當膨脹波從噴管唇部傳播到軸線附近時與對稱側的膨脹波交匯會帶來更加劇烈的膨脹，在軸線上膨脹程度最高處的靜壓值低于環境壓力。為了與射流外界的環境壓力平衡，會形成環形的斜激波，氣體在通過斜激波時會發生壓縮。但由于本工況欠膨脹程度過高，斜激波的角度超過了激波正常反射條件，會出現類似于馬赫反射的情況，在軸線附近形成了正激波馬赫盤，攔截激波與正激波在交點處產生反射激波。在初始時刻，靠近壁面y=0.8Dj的位置處向上游輻射出一道較強的波，波會在噴管唇部發生反射，反射波在剪切層附近向下游傳播，與新生成的波發生干涉并繼續傳播至沖擊平板，從而形成反饋環。

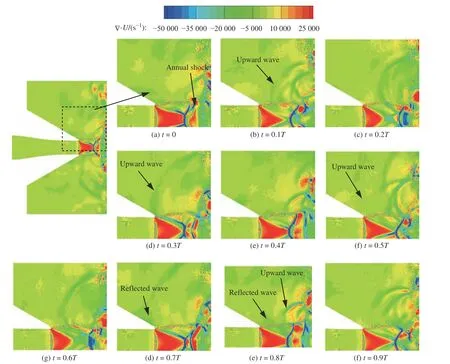
圖10 一個流動震蕩周期內的瞬態速度散度分布Fig. 10 Transient velocity divergence distribution during a flow oscillation period

為精確探究流場震蕩與反饋回路的周期，使用帶有Hanning窗的快速傅里葉變換對流場中的脈動壓力進行處理，樣本數N=1024，采樣間隔與數值模擬采樣間隔Δt相同。圖11和圖12分別為快速傅里葉變換得到的功率譜密度（PSD）在中心線和唇線上的分布，圖中示出了流場中的脈動壓力在fs=5212 Hz和倍頻2fs=10425 Hz時存在強烈的離散頻率。這與Henderson實驗中測得的沖擊單音頻率（10253 Hz）相符合。在圖11示出的中心線脈動壓力頻率分布和圖12示出的唇線脈動壓力頻率分布（圖中使用對數標尺）中可以看到，在fs以及其各倍頻處都有明顯的強烈離散頻率，該頻率對應的周期為T=1.92×10?4s，與前面觀測得到的周期T=2×10?4s基本相同。由于中心線上存在超聲速流動，在超聲速流動中脈動量較小，因此中心線上的數據存在一段低谷，而唇線上各處都有較高的脈動水平。

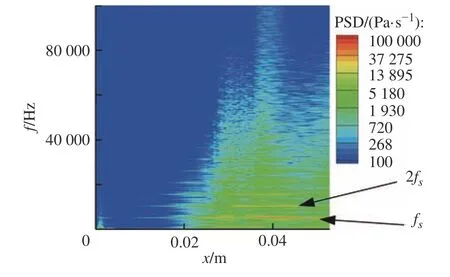
圖11 中心線脈動壓力頻率分布Fig. 11 Frequency distribution of pressure fluctuation on centerline

圖12 唇線脈動壓力頻率分布Fig. 12 Frequency distribution of pressure fluctuation on lip line

圖13、圖14分別示出了對應頻率為fs和2fs的脈動壓力分布，圖中示出了在正激波馬赫盤與反射激波的后方有頻率為fs脈動壓力分布，其位于軸線上x=1.6Dj處。并且，在壁面射流區中的渦環結構也以fs為主頻。在正激波馬赫盤與反射激波的前后均有頻率為2fs壓力脈動分布，集中于軸線上x=1.26Dj與x=1.6Dj處，并且存在反饋環的區域中，也分布有2fs的壓力脈動信號，這可以直接說明，反饋環的頻率與沖擊單音的頻率是相關的。

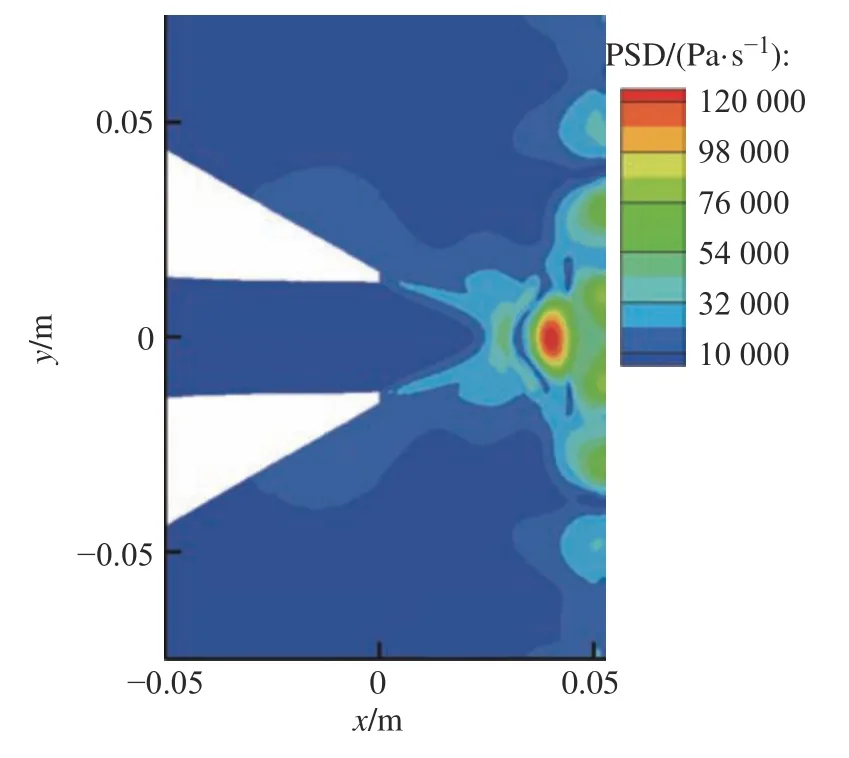
圖13 5 212 Hz脈動壓力幅值Fig. 13 Amplitude of pressure fluctuation at 5 212 Hz

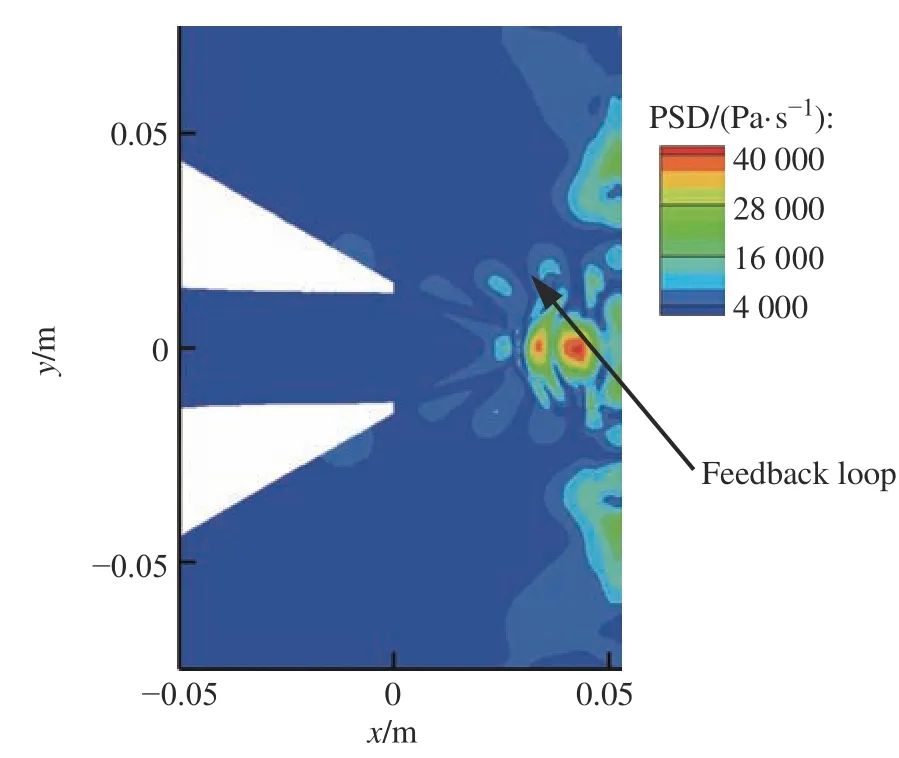
圖14 10 405 Hz脈動壓力幅值Fig. 14 Amplitude of pressure fluctuation at 10 405 Hz

2.3 本征正交分解分析

本征正交分解（Proper Orthogonal Decomposition，POD），也被稱為Karhunen-Loeve展開或主成分分析方法（Principal Components Analysis），是一種基于矩陣論的數據統計分析方法，廣泛應用于數據降維，流場分析等。POD的主要目的是為流場提供分析手段且保持其物理意義，同時著眼于使用動態系統的概念來預測流場，可以實現對復雜的非線性系統的線性降維處理。考慮脈動分量u′(x,ti) ，將其分解為時間系數an(t)與POD的空間模態 φni(x) ，即

本文使用Snapshot方法進行POD分解[17-18]，對仿真計算得到由M行空間點、N列采樣時間構成的原始數據矩陣AM×N，定義相關矩陣RN×N：

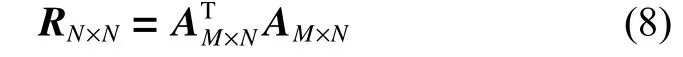
求解相關矩陣RN×N的特征值問題

得到相關矩陣RN×N的特征值λi與特征向量 φi。若原始數據矩陣AM×N為脈動速度，則λn可以表示第n階模態對流場中湍動能的貢獻。

定義第n階模態的能量貢獻率為

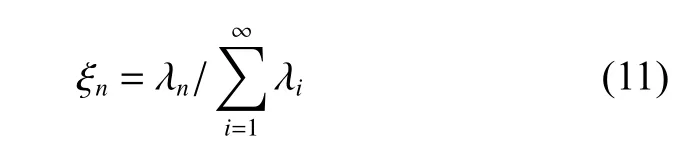
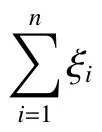
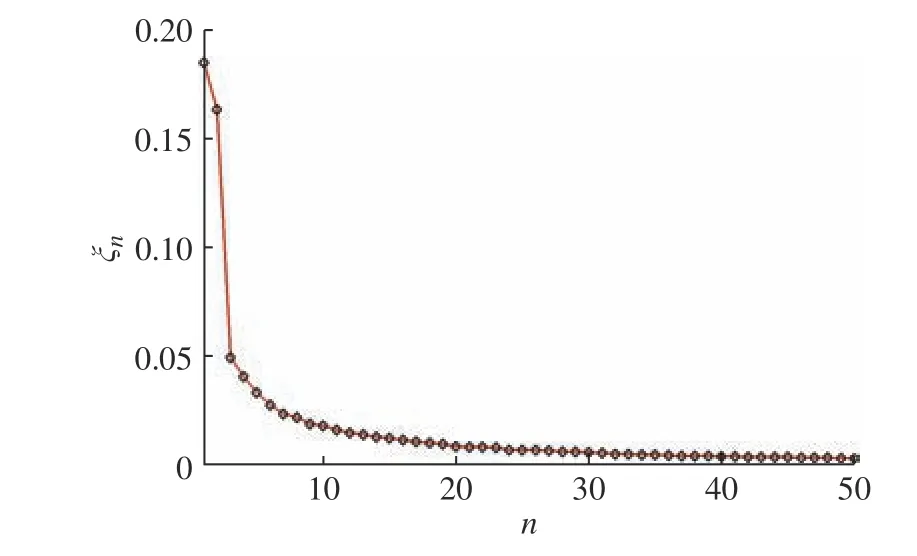
圖15 POD能量貢獻率Fig. 15 Energy contribution rate of POD modes

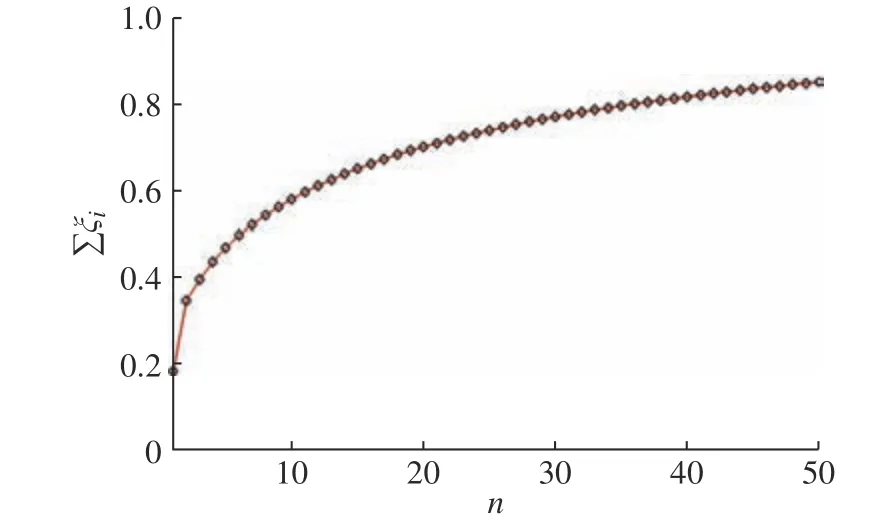
圖16 POD累計能量貢獻率Fig. 16 Cumulated energy contribution rate of POD modes

圖17示出了脈動速度的1、2、3、4、8階速度模態（各模態均以該模態最大幅值進行歸一化處理并記為 φˉ ）。1階模態是流場中能量占比最高的模態，可以反映噴流流場中主要的大尺度相干結構，具有較強的對稱性。在1階模態中，射流邊界、馬赫盤與斜激波后、再循環區以及壁面射流均具有較強的相關性。再循環區在斜激波后超聲速流的剪切作用下表現為對稱的環形渦結構，再循環區前有明顯的分界面。超聲速流與壁面射流交界處產生的渦結構沿徑向發展，并將外部環境流體卷吸到壁面射流中。在1、2階模態的壁面射流區域中捕捉到了沿徑向的模態對。3階模態主要反映了在射流邊界，再循環區與壁面射流的交界存在較強相關性。其主要現象為沿徑向射出的壁面射流導致在靠近壁面y=0.8Dj～1.6Dj處產生渦結構，卷吸流體回到再循環區與壁面射流的交界處。而4階模態表現為斜激波后的流動直接匯入壁面射流，這與前文提到的在再循環區與壁面射流的交界處的渦結構具有周期性相符合。8階模態捕捉到了在反饋環控制區域存在的相干結構，與圖10示出的反饋環相對應。

圖17 1、2、3、4、8階脈動速度模態Fig. 17 Velocity fluctuation plots of 1st, 2nd, 3rd, 4th, 8th POD mode

3 結 論

(1)馬赫盤在軸向震蕩，激波下行過程中，噴出的欠膨脹氣體有更充分的膨脹空間，因此可以達到更高的速度，從而導致穿過馬赫盤與斜激波的流體速度差增大，使得剪切作用增強，再循環區的影響范圍增大。

(2)在靠近壁面y=0.8Dj的位置輻射出一道較強的波動并向上游傳播，并經噴管唇部發生反射后，在剪切層附近向下游傳播，與新生成的波發生干涉并繼續傳播至沖擊平板，從而形成反饋環，它主導了沖擊單音的產生，本文通過對脈動壓力進行快速傅里葉變換，證實反饋環與沖擊單音具有相同的頻率。

(3)在壁面射流區中，超聲速流與壁面射流交界處受反饋作用產生大尺度環形渦結構，在其沿徑向發展的過程中，外部環境流體不斷被卷吸到壁面射流中，并且大尺度環形渦結構隨沖擊發生破碎，生成更小的渦旋結構。