帶時間窗的低碳車輛配送路徑優化研究

文/王浩青 鄭金諾

針對當前環境問題日益嚴峻，低碳車輛配送路徑優化在減少碳排放方面有著重要意義。在以往的車輛配送路徑問題中只考慮經濟成本最小而忽略了碳排放。本文首先將碳排放轉化為碳排放成本，構建了總成本最小的目標優化模型，其次采用蟻群算法對優化模型進行求解，最后通過算例驗證了模型的有效性，為減少車輛碳排放提供參考和決策支持。

0.引言。

近年來，物流活動成為了我社會經濟發展的必要條件，隨著配送需求不斷增加，配送車輛數量也隨之增加，勢必會產生更多的碳排放，實現低碳車輛配送路徑是解決環境的關鍵。優化車輛行駛路線，即求解車輛路徑問題（Vechicle Routing Problem，VRP），1959年由Dantzi和RamserP[1]首次提出，是0-1整數規劃的NP-Hard問題。Solomom[2]等首次引入時間窗概念，即（Time Windows VRP）TWVRP。Jabali[3]等提出了軟時間窗的VRP問題模型。低碳車輛路徑問題（Low-carbon Vehicle Routing Problem,LCVRP）是基于傳統車輛路徑問題（VRP）的研究基礎，加入了碳排放的約束。已有不少文獻研究了碳排放因素對物流運輸業的影響，當市場中存在碳交易機制時，物流配送路徑問題便需要考慮碳排放帶來的成本。在減少車輛碳排放方面，吳麗榮[4]等建立了車輛燃料消耗的模型并進行求解。康凱[5]等人在模糊約定時間窗車輛路徑優化問題研究中考慮了碳排放因素并轉化為碳排放成本。代楚楚和徐菱[6]建立了基于時間依賴車輛路徑問題模型的快遞企業低碳配送車輛路徑選擇模型，并設計了多種群遺傳算法對模型進行求解。王鈺青[7]等將車輛行駛路程、運輸途中載貨量和碳排放量進行綜合考慮，建立基于最小碳排放量的廣義旅行商模型來尋求最優配送路徑。本文從上述問題入手，研究考慮碳排放因素的帶時間窗車輛物流配送路徑優化問題，引入碳排放成本機制，構建以總成本為目標的數學模型，同時采用蟻群算法進行求解出最優路徑方案。

1.問題描述。

一個配送中心為多個客戶點提供配送服務，客戶點的坐標、時間窗、需求量已知，目標是求解出總成本最小化的最優路徑方案。為了界定研究范圍，作出如下假設：（1）車輛為同質車輛，車輛完成任務后返回配送中心（2）各個客戶點均有時間窗要求，不能提前或者延后服務（3）客戶需求量小于車輛最大裝載量（4）車輛配送過程中速度保持恒定，不受道路情況影響（5）車輛在客戶點服務時，不會產生碳排放。

2.模型構建

2.1 符號定義

為配送客戶點的集合，u∈U；U0為配送中心和客戶點構成的集合，U0=U∪{0}，0表示配送中心；A為節點之間弧的集合，A={（i，j），i≠j，i∈N，j∈N}；K為配送車輛k的集合，k∈K；qt為客戶點q的需求，且maxqt≤Q，i∈U；[ei，li]為客戶點i的服務時間窗；dij為客戶點i和客戶j之間的距離；r為每使用一輛車的租賃成本；v為車輛行駛速度；γ為二氧化碳排放系數；s為碳排放成本。

Xik為0-1變量，當節點i由車輛k服務時值為1，否則為0；Xik為0-1變量，當弧（i，j）上有車輛行駛時值為1，否則為0。yik為0-1變量，當車輛在弧（i，j）上行駛時值為1，否則為0。

2.2 碳排放計算公式。由于Barth的綜合油耗模型考慮到車輛載重、速度和行駛距離對車輛油耗的影響，能夠給出任意載重和速度組合下車輛勻速行駛時的綜合油耗，所以本文采用其油耗模型，并引入碳排放系數γ，以此將油耗量轉換為碳排放量，N表示發動機轉速，V表示機排量，v表示車輛速度，d表示行駛距離，μ代表車輛自重，f表示車輛的裝載量，ξ表示燃料與空氣質量比，A表示車輛正面表面積，κ表示常量，ηtf表示車輛轉動效率，θ表示道路角度，g表示引力常數，Cd表示空氣阻力系數，Cr表示滾動阻力系數，ρ表示空氣密度，λ=ξ/κψ，γ=1/（1000ηtfη），α=τgsinθ+gCrcosθ，β=0.5CdAρ，化簡后如式（1）所示，F=λ（kNV+γβv3+γα（μ+f）v）d/v=λ

式（1）可以分為三個部分，第一部分kNV/v可以認為是發動機模塊的油耗，為與行駛時間呈正比例關系的線性函數，第二部分γβdv2可以被認為是速度模塊的油耗，為速度的二次函數，第三個部分γα（μ+f）d為重量模塊的油耗，獨立于速度和行駛時間，與車重和行駛距離直接相關。

2.3 數學模型

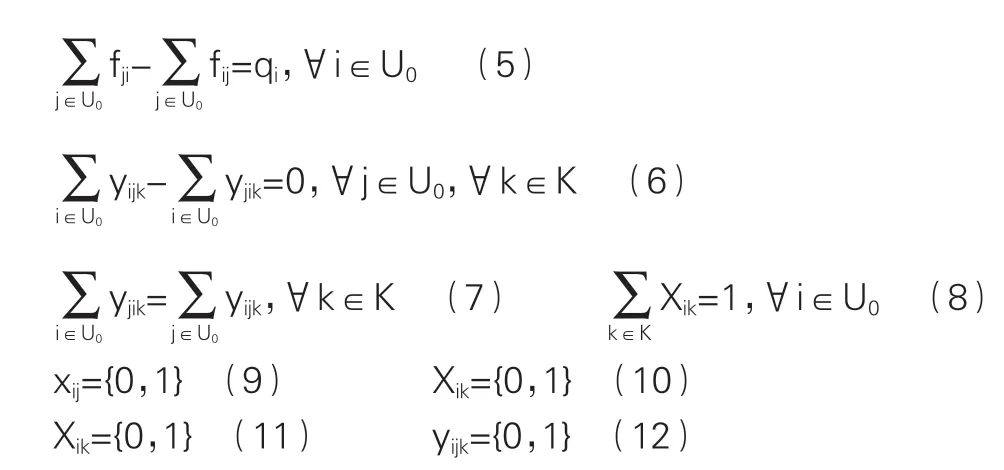
式（3）表示每輛車只使用一次；式（4)表示流量守恒；式（5）表示每個客戶需求得到滿足；式（6）表示車輛服務完客戶點離開；式（7）表示車輛到達和離開是同一客戶點；式（8）表示每個客戶只被服務一次；式（9）-（11）表示決策變量。

3.蟻群算法求解。

蟻群算法是螞蟻之間是相互幫助，如果螞蟻在一條沒有走過的路上行走時，會隨機選擇一條路，在此路程中會留下信息素，路徑越長，留下的信息素濃度會越少，相反，信息素的濃度就會越多，后面行走的螞蟻通過自身感知信息素濃度的高低來決定走哪條路，信息素濃度越高，螞蟻選擇這條路的概率就會越大。經過長時間后，螞蟻通過傳遞自身的信息素從而形成一種正反饋機制。最終，所有的螞蟻會找到一條距離最短的路徑也就是最優路徑。蟻群算法具有較強的魯棒性[8]，因為蟻群算法的參數較少，對初始解的依賴性低，對它的基本模型進行簡單修改便可以應用到其他眾多領域。因此在車輛配送中，車輛對初始路線選擇的隨機性較高，基于蟻群算法這一特性，在對車輛行駛路線搜索過程中不斷調整，從而獲取最優路徑。本文研究的配送車輛路徑規劃中，每個車輛代表螞蟻，各個客戶點與配送中心之間的相互距離表示行走的路線。基于上面所述的原理將車輛的行駛路線形成一個正反饋機制，在本文設計配送路線中，形成一個滿足約束條件的最短路徑，從而降低車輛產生的碳排放。蟻群算法在解決帶時間窗的車輛配送問題時，算法步驟如下：Step 1初始化蟻群算法各個參數，設置蟻群數量m，t時刻時弧（i，j）的信息素濃度為τij；Step 2每只螞蟻從配送中心出發，爬行路徑由信息素濃度確定，將所有在客戶點的螞蟻下一個訪問的客戶點集合存儲到禁忌表中；Step 3蟻群重復以下步驟，最后將所有客戶點遍歷一遍；Step 3.1通過轉移概率計算公式，螞蟻將選擇下一個客戶點。具體為螞蟻根據每條弧上的信息素濃度選擇下一個客戶點，假設螞蟻在時刻從客戶點i出發，選擇客戶點j的狀態轉移概率表達式為式（12）：

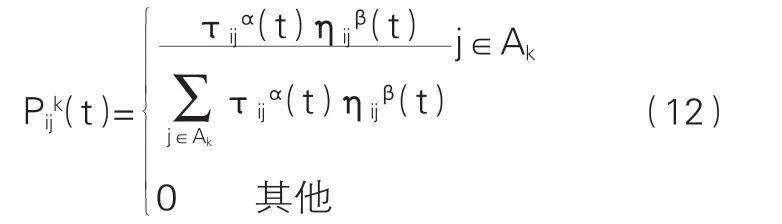
τij（t）表示客戶點i和客戶點j之間的信息量濃度，α表示信息素濃度，β為期望啟發因子，Ak表示車輛k可以被允許選擇的客戶點，ηij表示客戶點j對于客戶點i的啟發程度。Step 3.2如果客戶點i滿足約束條件，則螞蟻m轉移到客戶點；

Step 3.3將符合約束條件的客戶點加入到禁忌表中；

Step 4更新全局信息素。信息素濃度更新表達式為式（13）：

△τij（t，t+1）表示在（t，t+1）時間段內，弧上（i，j）的信息素增加量，ρ表示信息素揮發系數；

Step 5每次迭代Nc=Nc+1，如果Nc=Ncmax，則返回到Step2；否則就輸出最優解并結束算法。

4.算例分析。

為了驗證本文提出的模型有效性，現采用Solomon的VRP數據集中的算例C101對模型算法進行檢驗。選取數據集中1個配送中心和25個客戶點，蟻群算法參數設置為：m=100，Ncmax=100，α=1，β=3，ρ=0.8，車輛參數設定如下：r租賃成本=100，ξ空氣與燃料質量比=1，κ標準柴油燃料的熱值(kg/g)=44，ψ從克g/s到升l/s的換算系數=737，k發動機摩擦系數（kj/rev/l）=0.2，N發動機轉速（rev/s）=33，V發動機排量（l）=5，ρ空氣密度（kg/m3）=1.2，A迎風表面積m2=3.19，μ車輛自身重量（kg）=6300，g引力常數=9.8，θ道路角度=0，Cd氣動阻力系數=0.7，Cr滾動阻力系數=0.01，ε車輛傳動系效率=0.4，ω燃 油 機 效 率 參 數=0.45，γ碳 排 放 系 數=2.61（kg/l），s碳排放成本=20（kg/元），v車輛行駛速度=50（km/h）。在CPU為2.9GHz，內存為8GB，使用MATLAB2020a計算機上編程計算得到以下優化方案：當不考慮碳排放，以運輸成本最小為目標函數時，車輛總使用數為4輛，車輛總行駛距離為182.3257，租賃成本為400，碳排放量為403.2565；優化后，車輛總使用數為3輛車，車輛總行駛距離191.8136，最低碳排放量為400.3714，租賃成本為300，碳排放成本為8007.428，1號車輛配送路線為0→5→3→7→8→10→11→9→6→4→2→1→0，2號車輛配送路線為0→13→17→18→19→15→16→14→12→0，3號車輛配送路線為0→20→24→25→23→22→21→0。相比于優化前，雖然車輛總行駛距離增加了，但碳排放量減少了0.71%。以上結果僅僅是對于25個客戶點來進行計算求解，如果對于實際生活，減少的碳排量會更多。

5.結論

本文綜合考慮包含配送車輛租賃成本和碳排放成本，建立了考慮時間窗的低碳車輛配送路徑優化數學模型，采用蟻群算法求解所提模型，并通過具體算例對本文的模型和算法進行仿真，與不考慮碳排放的車輛配送路徑方案對比，可以得到優化后的路徑方案，這對于我國物流企業實施低碳物流有很大的促進作用。因此本文所建模型和求解算法對于帶時間窗的低碳車輛配送路徑規劃具有適用性和有效性，對低碳物流的發展提供了有效的支持。