利用趙爽弦圖解題3例
孫志東

【摘要】本文借助于趙爽弦圖中大小兩個正方形邊長之間的關系,解決了含趙爽弦圖或類趙爽弦圖的三個問題.
【關鍵詞】趙爽弦圖;大小正方形邊長的關系;類趙爽弦圖
三國時期的數學家趙爽創制了一幅“勾股圓方圖”(如圖1),他用形數結合的方法,給出了勾股定理的一種簡潔證明,這種證明方法構思巧妙,給我們很多啟發.
其實它是由四個全等的直角三角形拼成一個大正方形,中間恰好形成一個小正方形(如圖2).
設Rt△ABE的三邊分別為BE=a,AE=b(b>a),AB=c,則a2+b2=c2,且大、小兩個正方形的邊長分別為c,b-a.
抓住趙爽弦圖大、小正方形的邊長之間的關系,就抓住了趙爽弦圖的關鍵特征,可以靈活地來進行解題.下面舉三例來說明其應用.
例1如圖3,E,F,G,H分別為正方形ABCD各邊的中點,要使中間陰影部分小正方形的面積為5,則大正方形的邊長應該是()
由F,H為正方形對邊BC,AD的中點可知
AF∥CH,
選(C).
例2如圖4,在△ABC中,∠ACB=90°,以△ABC的各邊為邊分別作正方形BAHI,正方形BCFG,正方形CADE,延長BG,FG分別交AD,DE于點K,J,連接DH,IJ.圖中兩塊陰影部分面積分別記為S1,S2,若S1:S2=1:4,四邊形BAHE的面積為27,則四邊形MBNJ的面積為________.
解大正方形BAHI及其內部恰好符合弦圖結構,設BC=a,AC=b,AB=c,則
所以b2=27,
因為S1:S2=1:4,
所以a2=4(b-a)2,
因為SMBNJ=SBGJM+S△BNG=SAKGN+S△BNG
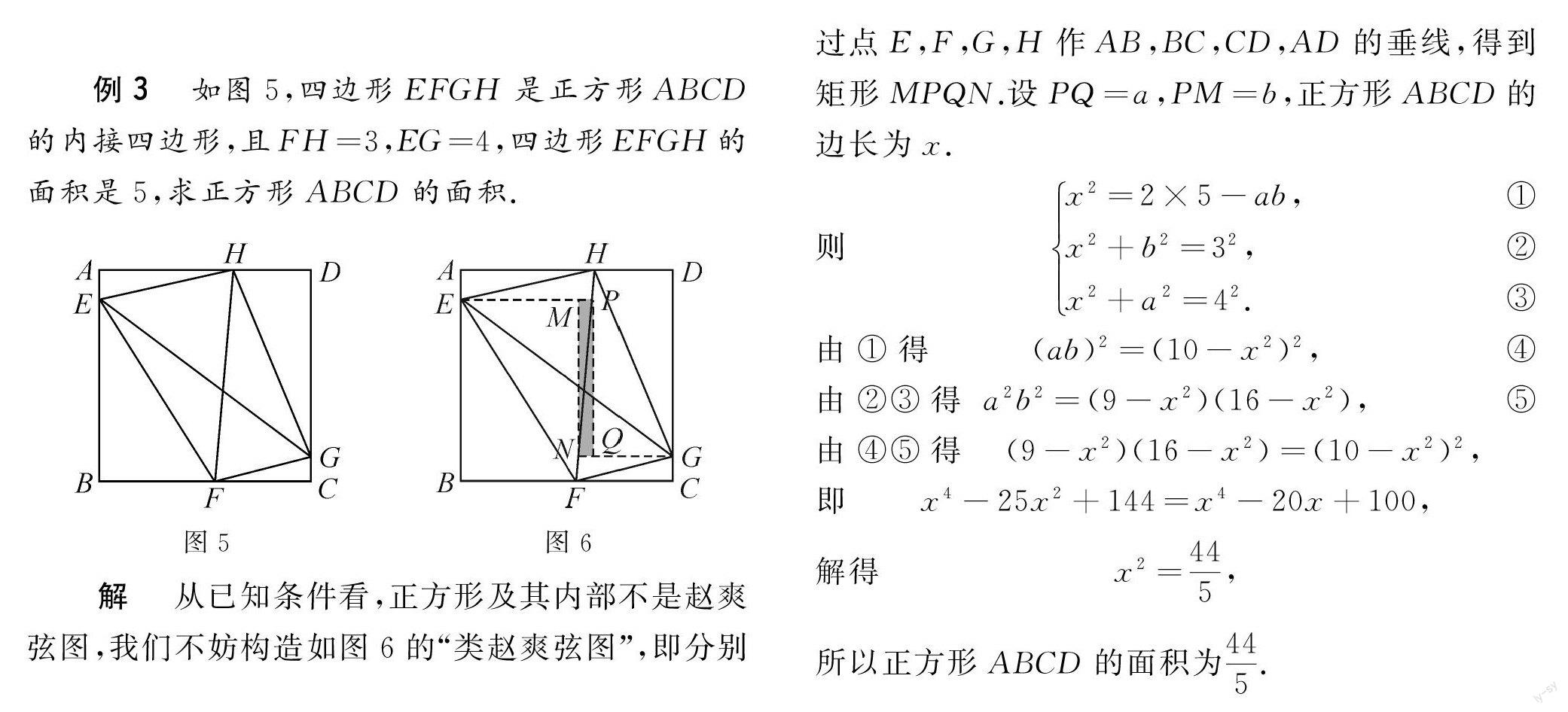
例3如圖5,四邊形EFGH是正方形ABCD的內接四邊形,且FH=3,EG=4,四邊形EFGH的面積是5,求正方形ABCD的面積.
解從已知條件看,正方形及其內部不是趙爽弦圖,我們不妨構造如圖6的“類趙爽弦圖”,即分別
過點E,F,G,H作AB,BC,CD,AD的垂線,得到矩形MPQN.設PQ=a,PM=b,正方形ABCD的邊長為x.
由①得(ab)2=(10-x2)2,④
由②③得a2b2=(9-x2)(16-x2),⑤
由④⑤得(9-x2)(16-x2)=(10-x2)2,
即x4-25x2+144=x4-20x+100,

