小學數學高階思維能力培養的有效策略分析*

臺運兵

(合肥市方橋小學 安徽合肥 230011)

高階思維能力是指發生在較高認知水平層次上的心智活動或認知能力，它在教學目標分類中表現為分析、評價和創造。隨著核心素養理念的提出和深入研究，近年來，關于學生數學高階思維能力的探討熱度越來越高，培養和發展學生的高階思維能力也是當今社會對高素質創新型人才的重要要求。

一、小學數學高階思維能力培養的現狀分析

在傳統的數學課堂中，教師是知識的傳遞者，而學生則是被動的接收者，填鴨式的教學導致學生不會主動思考，從不批判、從不質疑，更難有什么創新能力。雖然課改已進行多年，但在一些數學教學中，至今仍然存在著對學生進行低階思維能力的重復訓練。通過分析合肥市學業質量綠色指標評價數據，發現全市區域之間、校際之間、班級之間的學生高階思維能力的差異性十分顯著，說明教師們在教學目標的設定、教學策略的選擇、教學評價的運用上還或多或少存在一些問題。

通過分別對學生和教師問卷的調查結果進行數據分析發現，當前小學數學高階思維能力培養的情況不論從學生的角度，還是從教師的角度來看，都或多或少地存在一些問題。主要表現在以下四點：學生對基礎知識的儲備相對匱乏；學生缺乏自主意識和批判精神；教師缺乏對學生高階思維能力培養的意識；教師缺乏對高階思維能力的正確引導和評價。

二、培養學生數學高階思維能力的有效策略

(一)精心設問，引領建構，培養數學高階思維能力

數學是一門邏輯性、系統性強的基礎學科，前后知識的關聯度大，整個學習過程呈螺旋上升式。作為教師，應認真研讀教材，充分挖掘知識內在的聯系，尋找前后知識的連接點，為學生的思維發展構建一個適宜的生長點。在數學課堂教學過程中，教師要能根據具體學情精心設置問題，引領學生順著問題拾級而上，逐步突破，在知識的建構過程中，培養其數學高階思維能力。

如教學蘇教版五年級上冊《小數加法和減法》時，設置一個生活化的情境，出示商店購物的場景圖，讓學生觀察獲取其中的數學信息：小剛買一個講義夾用了4.75元，小紅買了一個筆記本用了3.4元。接著提出問題：小剛和小紅一共用了多少元？學生很容易能列出算式：4.75+3.4。為了引導學生自主探究建構新知，教師預設如下四個問題：

第一個問題：這道加法算式有什么特點？

第二個問題：你打算如何計算？

第三個問題：小數加法和整數加法有什么相同點，又有什么不同點？

第四個問題：在計算小數加法時要注意些什么？

通過這樣層次鮮明、連續性強的“問題串”設計，直指知識本質，直通學生的“最近發展區”。同時，也改變了傳統課堂上“滿堂灌”的現象，給學生更多思考的時間和空間，能積極調動學生的思維建構，學生也能在教師的引領下逐步培養分析問題、解決問題的能力。

(二)自主探索，深度學習，發展數學高階思維能力

深度學習是一種高階層的思維活動，不同于“死記硬背”的淺層學習。數學的深度學習，應該是學生在教師的引領下，完整的經歷體驗探究學習的過程，能夠積極主動地運用數學方法和思想去分析問題、解決問題。

例如，在教學蘇教版五年級下冊《和的奇偶性》時，首先組織學生試著寫一些兩個非零自然數相加的算式，通過觀察、比較、歸納，提出“奇數+偶數→奇數，奇數+奇數→偶數，偶數+偶數→偶數”等猜想。接著，引導學生對猜想進行驗證，學生幾乎一致都采用計算的方法來驗證說明和的奇偶性情況。但是計算只是學生的淺層思維。所以，還需要通過幾何直觀，幫助學生建立模型，利用數形結合的思想，讓學生更加充分地感受奇偶的本質特性，使學生更加直觀、更加深刻地明白規律中蘊含的數學道理。

如在驗證“奇數+奇數→偶數”這條猜想時，首先，用如圖1中的圓片分別表示兩個奇數。

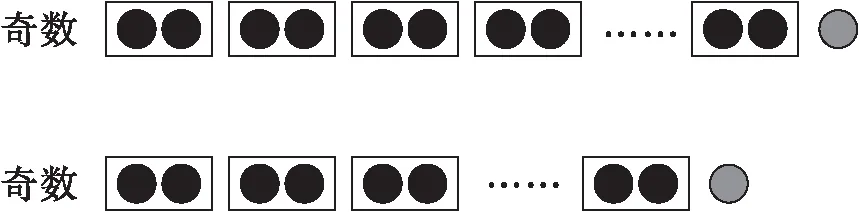
圖1 圓片圖形分別表示兩個奇數

接著，通過圖形重組配對(如圖2所示)，發現和是偶數。

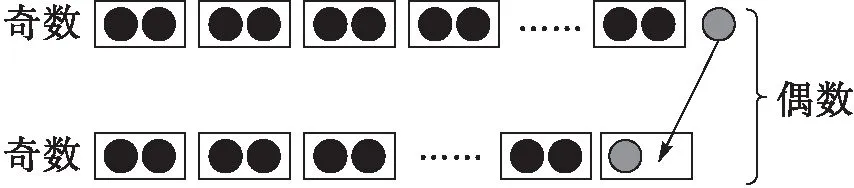
圖2 動態演示驗證“奇數+奇數→偶數”

這里的圖形很好地展示了奇數與偶數的本質性區別：能否被2整除。正是依托這一本源性知識，讓學生在拾級而上的探究過程中明確方法和結論，層層遞進。通過此環節，可巧妙地引導學生進行深度研究，從而增強學生的元認知體驗。教師不應只停留在計算的表面，而應組織學生進行深度研究，由數到圖形，再由圖形聯系數，每個學生都在經歷思維的碰撞，在體驗與反思中學習，有效地訓練了思維的靈活性和深刻性。這種教學模式真正做到了用數學的方法研究問題，用數學的思想探究規律，使學生在學習的過程養成觀察比較、理性思考等良好的品質，讓學生的高階思維能力得到長足發展。

(三)優化練習，分層設計，提升數學高階思維能力

作業布置是數學教學中不可缺少的部分，也是評價學生學習效果的重要手段之一。好的作業設計，能夠有效地激發學生的學習興趣，促進和提高學生的分析、評價和創造能力，更有利于學生在獨立思考的過程中提升自己的高階思維能力。

但目前，多數教師在布置作業時，還是以機械性、重復式的練習為主，嚴重影響了學生的積極性和興趣，不利于學生的思維能力發展。教師要清楚地認識到學生之間的差異性是客觀存在的，學生的思維發展也不盡相同。因此，教師要有針對性地設計分層次的作業練習，讓全體學生都能得到合適的鍛煉和提高，真正做到因材施教。

數學高階思維能力的培養不是一蹴而就的，教師需要在課前、課中、課后等方面多維度地進行設計思考。教師應注重在數學教學中嵌入有價值、值得思考的問題，引導學生在問題思考中建構知識，在問題思考中拓展思維的廣度和深度，努力為學生思維的發展尋找合適的生長點和延伸點，逐步培養學生的抽象思維、推理思維、批判思維、創新思維等，進而促進小學生數學高階思維能力的發展。