初等數論知識在小學數學中的滲透

趙 艷，李鳳清

（1.蓬溪縣實驗小學，四川 蓬溪 629100；2.四川職業技術學院 教師教育學院，四川 遂寧 629000）

初等數論主要研究整數的性質與規律，與小學數學知識有著密切的聯系。初等數論知識中的整數、整除、數的整除特征、素數、最大公因數、最小公倍數等知識既讓學生增強對整數性質的了解，又為分數等知識的進一步學習奠基，還增強學生對數學史以及數論方面的數學家的了解，培育數學文化，激發學生的學習興趣。如何以小學數學教材中“數的整除”一章中所展現知識內容為主導，找點發揮延伸，訓練學生解決問題的能力，滲透初等數論的初步知識與思想方法，下面我們從幾個方面以案例說明。

一、突出整數以及整除特性，結合一些運算性質解決問題

初等數論是研究整數的性質與規律，而小學數學中，有很多的整數問題，如人的個數、雞的只數、分數的分子分母等皆為整數，突出整數特性，以及整除的概念。合理結合相關數學知識來解決問題，可以培養學生正確認識整數問題，提高解決整數問題的能力。

案例1在下面的括號里填上最簡分數，使下面式子成立。

案例3 將數1,2,3,4,5,6,7,8,9 這九個數分別填在九宮格的九個格中，使每行、每列、兩條對角線上三個數的和都相等。

分析：因為每行三個數之和相等，那么三行九個數之和就等于1,2,3,4,5,6,7,8,9 之和45，那么每行之和就為45÷3 = 15，故每列三個數之和與對角線三個數之和均為15。

由于第二行、第二列、主對角線、次對角線之12 個數之和就為15×4 = 60，這12 個數至少包含1,2,3,4,5,6,7,8,9，而1,2,3,4,5,6,7,8,9 之和為45，還多出60 - 45 = 15，顯然是由于最中間格多算了3 次，故中間格填的數為15÷3 = 5。

1,2,3,4,5,6,7,8,9 這九個數中，其和等于15的三個數中若包含1，只有1,5,9 與1,6,8 兩種情形，故1 只能填邊不能填角，則可以填出：

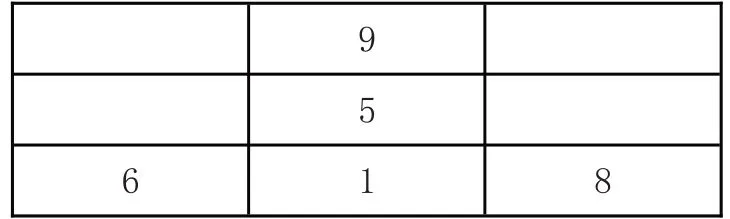
由此運用（行、列、對角線）三個數之和為15即可以填出其余四個格中的數。

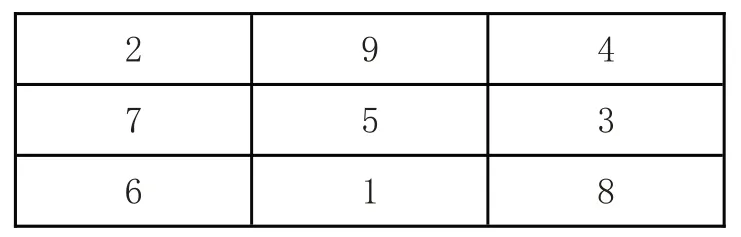
上面表格常被稱為河洛圖，又叫“河圖洛書”，是關于中國古代文明的著名傳說。六七千年前，龍馬躍出黃河，身負河圖；神龜浮出洛水，背呈洛書。伏羲根據河圖洛書繪制了八卦。之后大禹治水，河伯獻河圖，宓妃獻洛書，使得大禹終于戰勝洪水[1-3]。

案例3 運用整數的運算特性，抓住中間格這個關鍵與1 的位置，順利解決了問題，還對學生滲透中華傳統文化。

案例4法國數學家費馬發現F0= 220+ 1 = 3，F1= 221+ 1 = 5，F2= 222+ 1 = 17，F3= 223+ 1 =257，F4= 224+ 1 = 65537 都是素數，因為第5 個數F5= 225+ 1 = 232+ 1 實在太大了，費馬認為這個數還是素數，于是在1640 年提出了以下猜想：形如Fn= 22n+ 1 的數都是素數。后來人們就把形如22n+ 1 的數叫費馬數，很多人甚至將22n+ 1 稱為素數公式。大約過了92 年，即1732 年，偉大的數學家歐拉算出F5= 641×6700417，也就是說F5不是素數，宣布了費馬的這個猜想不成立，它不能作為一個求質數的公式，讓人們在尋求素數公式的追求中受到一次沉重地打擊。

其實，我們知道

216= 211×25= 2048×32 =(641×3 + 125)×32 = 641×96 + 4000 = 641×102 + 154，那 么216除 以641 余154，那么232除以641 就 與1542除以641 的余數相同，由于1542= 23716，而23716 除以641 余640，故232除以641 就余640，故232+ 1 就能被641 整除，故F5是一個合數，不是素數。

二、明確數的整除特征，滲透初等數論中同余的思想

運用整數的奇偶特征與性質，如奇數不等于偶數，奇數個奇數的和為奇數，偶數個奇數的和為偶數等等來解決一些問題，就可以轉繁為簡，突出本質。

案例536 口缸，九只船來裝，裝單不裝雙，試試怎么裝？

該題中，九個奇數的和為奇數，而36 為偶數，由于奇數不等于偶數，因此不存在符合條件的方案。（民間把36 口缸偷換成三石六口缸而成為有解題目）

案例6某次展覽為一個5×5 的方形展區，含一個門廳與24 個展室，如下圖，每相鄰兩個展室均有門可通，參觀者須從門廳開始到各展室觀看展覽，之后從門廳出去。請問是否存在一條路徑，不重復不遺漏地觀看完24 個展室。

分析 我們將24 個展室標記為奇展室與偶展室兩類，如下圖：

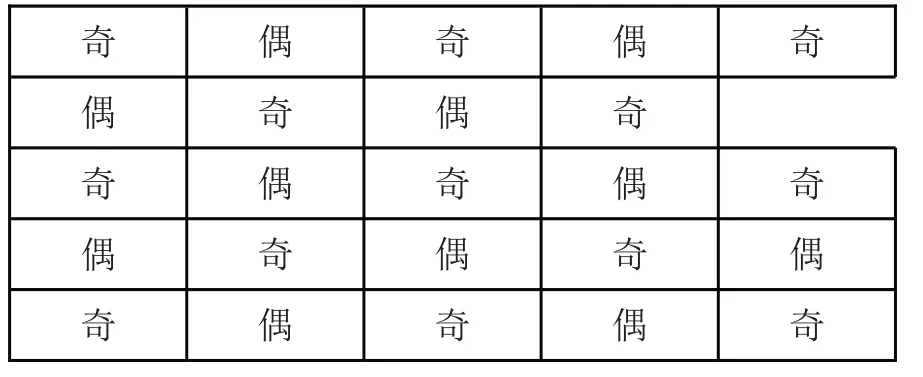
那么參觀者只能從奇展室到偶展室，或者從偶展室到奇展室，其路線必然是：

奇→偶→奇→偶→奇→偶…，則應該12 個奇與12 個偶，而圖中有13 個奇，11 個偶，故這樣的路徑是不存在的。

我們運用奇偶分類，巧妙解決問題，對培養學生思維的深刻性很有幫助。

學生理解能被2、5 整除的數的特征，我們還要講清道理，是任何一個整數N總可以分解成若干個10 加上個位數，即N= 10a+b，由于10a能被2、5 整除，那么當個位能被2、5 整除時，當然N就能被2、5 整除。

我們可以將上面這個知識點延伸[4]，得到：

N除以2（或5）余幾，關鍵看N的個位，個位上的數除以2（或5）余幾，那么N除以2（或5）就余幾。

繼續延伸：

N除以4（或25）余幾，關鍵看N的后兩位，后兩位上的數除以4（或25）余幾，那么N除以4（或25）就余幾。

N除以8（或125）余幾，關鍵看N的后三位，后三位上的數除以8（或125）余幾，那么N除以8（或125）就余幾。

（我們可以把這類性質稱為整除特征的響尾蛇特性）

大家知道9,99,999,9999,…,能被3（或9）整除，把這些數加上1，再除以3（或9）就該余1，因此10,100,1000,10000,…,等數除以3（或9）就該余1，那么我們就知道最高位是a，后面各位均為0 的整數除以3（或9）就該余a，如423 除以9 就轉化為400 + 20 + 3 除以9，400 除以9 余數就為4，20 除以9 就余2，3 除以9 就余3，故423 除以9 的余數就為4 + 2 + 3，即能被9 整除。

案例7將1，2，3，…，9 這九個數字分別填進下面九個空中，使等式成立。

將符合條件的所填三個三位數相加，即□□□+□□□+□□□，易知這可拆分成（□+□+□）×100+（□+□+□）×10+（□+□+□），可知它除以9 后的余數與（□+□+□）×1+（□+□+□）×1+（□+□+□）除以9 的余數相同，而（□+□+□）×1+（□+□+□）×1+（□+□+□）等于1+2+3+4+5+6+7+8+9=45，能夠被9 整除，可見□□□+□□□+□□□能被9 整除，而□□□+□□□+□□□為和□□□的兩倍，它能被9 整除，那么和□□□能被9 整除（易知和這個三位數□□□的百十個三個位置上的數加起來為18。）。

例如，取和為918，則□□□+□□□=918，即可迅速填出243+675=918，645+273=918 等答案。依此方法我們可以得出所有的正確答案。

同余是初等數論中的重要概念，利用同余的思想方法來解決問題常常事倍功半。

設a為一位數，由于1、100、10000、1000000 這樣 的 數 除 以11 均 余1，那 么a,a×100,a×10000,a×1000000,…這樣的數除以11 的余數為a；設b為一位數，由于10、1000、100000、10000000這 樣 的 數 除 以11 均 余10，那 么b×10,b×1000,b×100000,b×10000000,… 這樣的數除以11 的余數為10b，總體特征為：一個整數去掉末尾偶數個零，除以11 后的余數不變。如求239674 除以11 余多少，就是(200000 + 30000 + 9000 +600 + 70 + 4)÷11 余多少，那么就等價于(20 +3+ 90 + 6 + 70 + 4)÷11 余多少，就是193÷11 余多少，即得余數為6。

還可以給小學生介紹1001 這個有趣的數，《一千零一夜》是1001 個美麗的童話，可以七個為一組，也可以十一個為一組，也可以十三個為一組，也就是1001 = 7×11×13，說明1001 可以被7或11 或13 整除，我們把六位數239674 分解為239×1000 + 674，再將它轉化為與1001 有關系的式 子 239×1001 + 674 - 239 = 239×1001 + 435，故：

239674÷11 的余數與435÷11 的余數相同；

239674÷7 的余數與435÷7 的余數相同；

239674÷13 的余數與435÷13 的余數相同；

這樣就把一個六位數求余數的問題轉化為三位數求余數問題，化繁為簡，解決問題。

按西方人的三位分節標注多位整數，如將123789668 這個數標注為123，789，668，這樣就可以得到三個三位數123，789，668，由于123000000=123000×1001-123000，即可變形為123000×1001-123×1001+123，故123000000 除以7 或11 或13 的余數與123 除以7 或11 或13 的余數相同，由上可知789668 除 以7 或11 或13 與668-789 除 以7 或11或13 的 余數相同，故123789668 除 以7 或11 或13的余數就與123-789+668 除以7 或11 或13 的余數相同，即余數為2。

并且我們還可以進一步總結出下面結論：

一個多位數N按三位分節，把最末一節的三位數記為N1，倒數第二節的三位數為N2，倒數第三節的三位數為N3，…，那么N除以7 或11 或13與N1-N2+N3-N4+ …除以7 或11 或13 的余 數相同。

三、發掘教材內容，滲透兩個數的最大公約數、最小公倍數的簡單性質

教材中求兩個數的最大公約數與最小公倍數使用的是短除法，把它模式化為下圖：

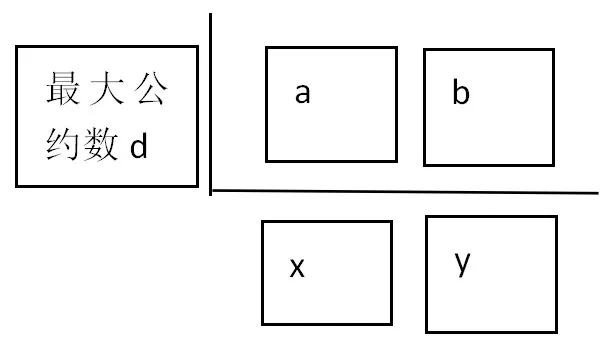
可知x,y互質，最小公倍數為dxy，a=dx,b=dy。即可得出結論[5]：兩數的最大公約數與最小公倍數的乘積等于兩數乘積。

案例8兩個數的積是1260，它們的最大公約數是6，求這兩個數。

從上面學生非常熟悉的短除法可以看出，這兩個數的最大公約數為6 時，必滿足x,y互質，那么這兩個數分別為6x,6y，最小公倍數為6xy，那么乘積為36xy= 1260，即可知xy= 35，即可知x=1,y= 35 或者x= 5,y= 7。即得兩數為6 與210 或者為30 與42。

案例9兩個數的最大公約數為10，它們的最小公倍數為420，求這兩個數。

由上面短除法可知兩個數分別為10x,10y，最小公倍數為10xy，則10xy= 420，即可知xy= 42，由于x,y互質，即可知x= 1,y= 42 或者x= 2,y=21 或者x= 3,y= 14 或者x= 6,y= 7。即得兩數為10 與420，或者為20 與210，或者為30 與140，或者為60 與70。

四、滲透整數標準分解思想，化整為零解決問題

向學生說明，由于素數不可再分解出比它小的質因數，故大于1 的整數都可以分解成素數的乘積，即可以寫成2()3()5()7()…p()的形式[5]。我們先研究其局部2()、3()、…、p()的一些性質，再結合初等數論初步知識研究這些局部性質與整體性質的聯系，滲透整數標準分解思想，化整為零解決問題[6]。

案例101000 的約數有多少個？所有約數的和是多少？

常規解法為先寫出1000 的所有約數。我們可以讓學生進一步了解一個事實，若b是a的約數，那么b的質因數必然是a的質因數。我們將1000 分解質因數為23×53，那么1000 的約數分解質因數就必然表示為2()5()的形式。23有1，2，4，8 四個約數，53有1，5，25，125 四個約數，23的任何一個約數與53的任何一個約數相乘都是1000 的約數，那么就有下面結論：23的約數個數4 與53的約數個數4 相乘就得到1000 的約數個數，即16，23所有約數的和15 與53的所有約數的和156 相乘就是1000 的所有約數的和2340。

對于這類問題，通過對1000 的標準分解23×53，轉化為求23的約數個數、約數和與53的約數個數、約數和的問題，先化整為零，再從局部結果得出整體結果，且體現基本元素思想。

五、適度拓寬素數的相關知識，滲透初等數論方面的數學文化

向學生介紹素數的知識的同時，適度介紹素數研究的歷史與現狀，介紹我國在數論研究方面的數學家，如華羅庚、陳景潤等，還要抓出一些案例，使學生了解素數的分布、篩法等初步知識。

案例11 介紹孿生素數的概念與研究現狀（孿生素數是否有無數多對，現在發現的最大的孿生素數等）。如5 與7，11 與13，17 與19 等就是孿生素數，問題：大于3 的兩個孿生素數的乘積加上1 后一定是（）的倍數。

知識點：除2 與3 之外的素數都緊挨在6 的倍數前或后（為什么？6n- 2,6n+ 2 是偶數，6n+ 3是3 的倍數），則孿生素數總在某一個6 的倍數前與后，這兩個數就可以表示為6n- 1,6n+ 1，由于(6n- 1)(6n+ 1)+ 1 = 36n2，即可知填36。

拓展：p為大于3 的素數，那么p2- 1 一定是（）的倍數，為什么？

上面是我們對小學生滲透初等數論知識的一點做法。我們從多年的教學感受認識到，緊貼教材，適度發揮，不僅能開發學生的智力，增強數學核心素養，還能發現一些有數學天賦的孩子。