大方捆打捆機壓縮室輕量化研究

閆振洋 杜沖沖

1.石家莊郵電職業技術學院 河北石家莊 050022；2.三一重工股份有限公司 湖南長沙 410100

我國是農業大國，秸稈和牧草資源豐富，打捆后再利用可以提高資源利用率[1]。牧草秸稈打捆機是實現農業機械化與農業生物資源利用的主要設備之一，大方捆打捆機由于其工作效率高，需求量逐年增加。高雄等對大方草捆壓捆機喂入機構進行運動分析與優化，增加了喂入量[2]。郭輝等設計了一種基于工作負荷反饋的輪式自走方捆打捆機，降低了打捆機行走的動靜偏差與調整時間[3]。王國權等對秸稈撿拾打捆機的撿拾器進行動力學仿真研究，提高了撿拾效率[4]。陳鋒對大方捆打捆機進行壓縮機構設計及壓縮試驗研究，獲得合適的參數與結構[5]。

然而對大方捆打捆機壓縮室的設計研究較少，主要參考國外尺寸與壁厚，或者根據經驗進行設計加工。對大方捆壓縮室進行參數化建模，采用基于拉格朗日的非線性規格優化算法進行壓縮室輕量化。

1 參數化模型

Creo具有Pro/Engineer的參數化技術、CoCreate的直接建模技術和ProductView的三維可視化技術三者的優勢，利用Creo建立900mm×1200mm×2000mm大方捆打捆機壓縮室結構參數化模型，如圖1所示。共計8個參數，其中加強筋厚度為DS_D1；加強筋寬度為DS_D；第一加強筋距離壓縮室的端口的距離為DS_L1；第三加強筋距離壓縮室的出口的距離為DS_L2；第二加強筋與第一加強筋的距離為DS_L3；第四加強筋距離出口的距離為DS_L5；第五加強筋距離出口的距離為DS_L4。

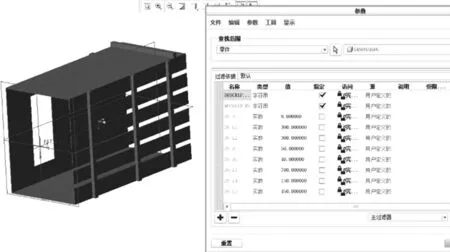
圖1 壓縮室參數化模型

8個參數優化過程非常消耗計算資源，在參數優化之前進行參數關聯性分析很有必要，可以獲得參數與輸出之間的敏感度，識別主要參數，剔除不重要的參數，從而簡化計算，節約計算成本。建立Creo與ANSYS之間數據交換接口，將有限元分析結果中的質量、最大應力以及最大變形作為輸出。壓縮室輸入參數和輸出參數敏感度如圖2所示。

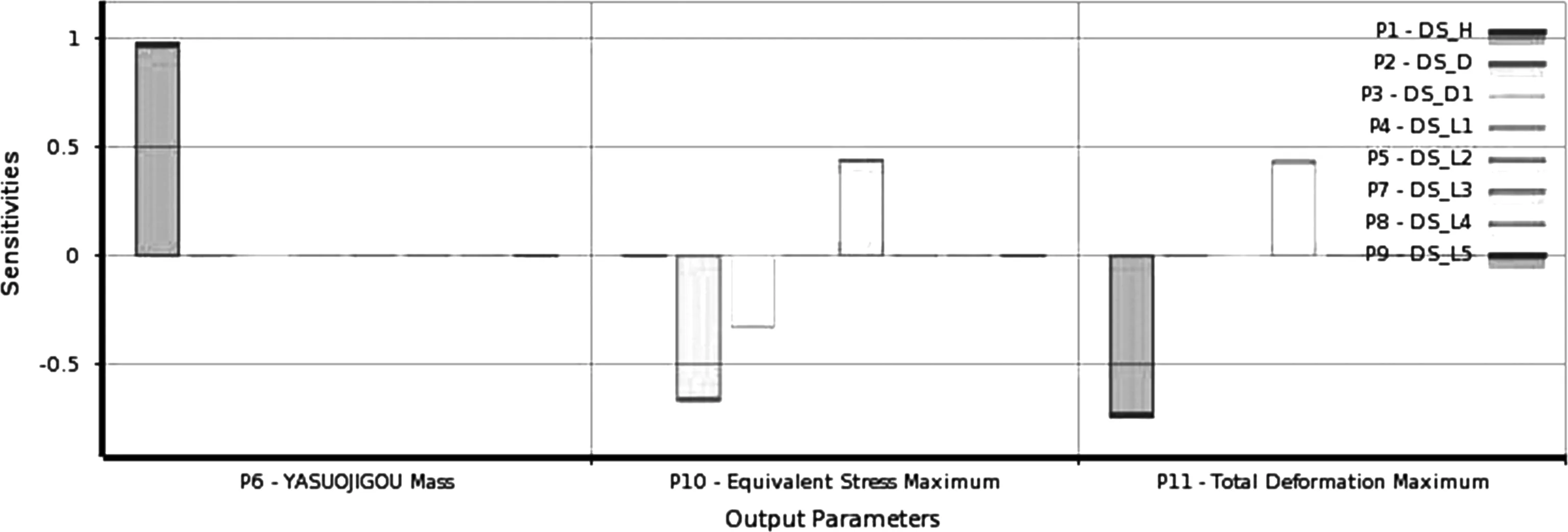
圖2 參數敏感度

DS_H厚度對質量和變形敏感度最大，DS_D1對應力敏感度最高。關聯性閥值為0.5，即小于0.5的為次要參數，大于0.5為主要參數。在八個結構參數的計算中，DS_H，DS_D，DS_D1，DS_L1，DS_L2為主要參數，DS_L3，DS_L4，DS_L5為次要參數，如圖3所示。

圖3 參數關聯度分析

2 Kriging代理模型

代理模型是指在進行優化設計的時候可以“代替”那些計算復雜且費時的數值分析或者有限元模型的數學模型，又被稱為“近似模型”“響應面模型”或“元模型”[6-7]。設原函數為y(x)，Kriging模型可以表示為：

yi(x)=f(x)Tβi+zi(x)i=1，2，…，q

(1)

式中：f(x)T為已知的回歸模型，一般為多項式函數，βi為回歸系數，zi(x)為隨機過程函數，它的均值為0，方差為σ2，協方差矩陣為：

cov[z(xi)，z(vi)]=σ2R(xi，vi)

(2)

其中，R(xi，vi)為兩個數據點x、v之間的變異函數，可采用高斯函數類型，表達式如下：

(3)

式中：n為維數，θ為相關性參數。

由實驗數據樣點值和它們對應的計算值，組成一個相關矩陣：

(4)

式中：m為樣本點個數。

設x0為預測點，其與樣本數據點之間的相關矩陣為：

(5)

由樣本點組成的相關矩陣為：

(6)

根據樣本點，利用拉格朗日乘子法與極大似然估計可以獲得相關性參數θ、β和σ2的估計值：

(8)

聯立上述方程可以獲得預測點x0的估計值為：

(9)

為了建立Kriging近似模型，需要一定數量的樣本數據，拉丁超立方抽樣法具有優異的整體空間均布填充能力，可以保證在多參數區間內獲得較好的實驗樣本點[8]。拉丁超立方體抽樣的基本步驟是：

(1)將每一維分成互不重疊的m個區間，使得每個區間具有相同的概率。

(2)在每一維里的每一個區間中隨機的抽取一個點；

(3)然后從每一維里隨機抽出的步驟(2)中選取的點將它們組成向量。

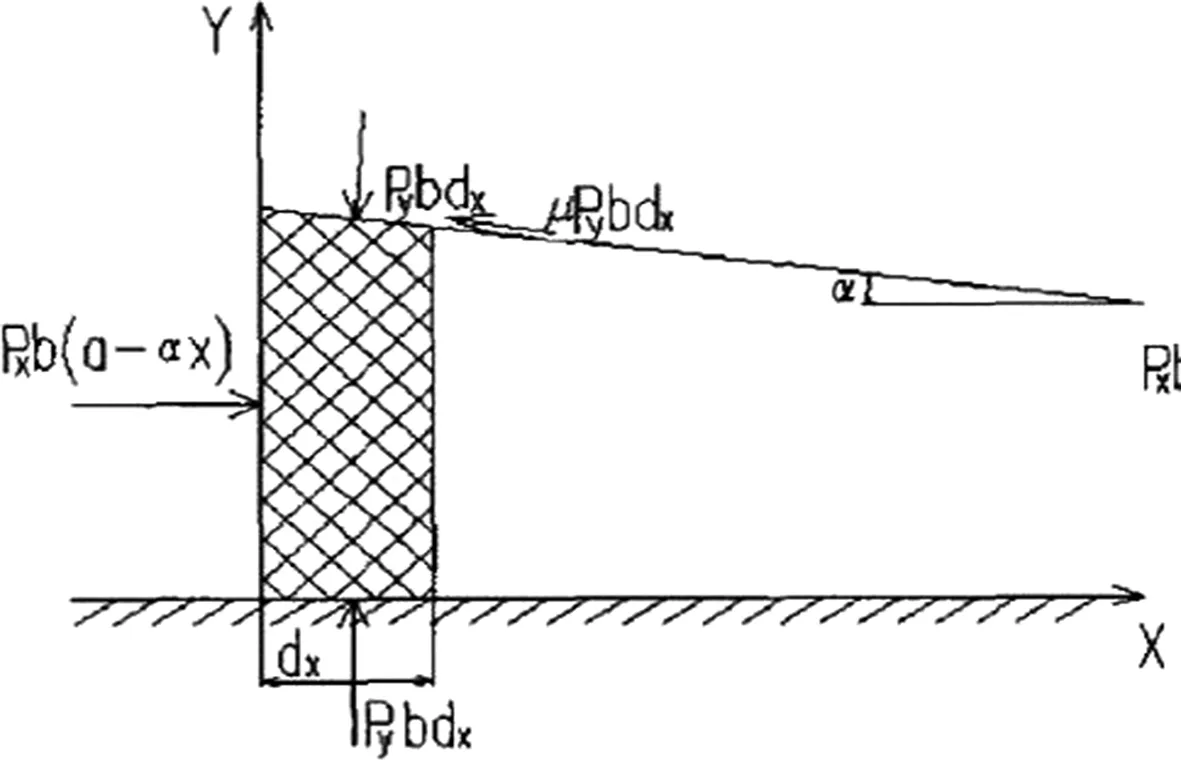
A側視圖圖4 壓縮室截面圖

從壓縮室的入口到出口存在一定的坡度如圖4所示，利用坡度與壓縮活塞對牧草等原料進行壓縮，根據壓縮理論[5]，壓縮室壁面力與活塞力平衡公式如下：

(10)

在ANSYS軟件workbench操作平臺中，將壓縮室入口和地面設置為固定約束條件，其余壁面以壓力函數作為負載，材料選為Q235，輸入參數為5個主要參數，輸出為最大應力和質量，獲取超拉丁立方樣本點數據如圖5所示。

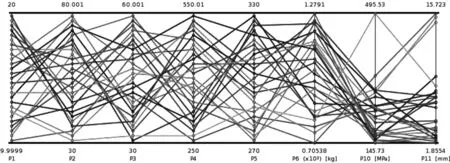
圖5 拉丁超立方樣本點

根據拉丁超立方抽樣的樣本點建立Kriging代理模型，設置驗證點并采用響應點和驗證點的數值進行對比。相同參數下Kriging代理模型響應點最大應力為197.5MPa，驗證點最大應力為200MPa，誤差為1.26%，質量誤差為0.02%，誤差在允許范圍內。

圖6 參數DS_H，DS_D與輸出質量響應

圖6為壓縮室輸入參數DS_H，DS_D與輸出質量響應面，輸出壓縮室質量隨著DS_H，DS_D增加而增加。圖7為輸入參數DS_D，DS_D1與輸出最大應力響應面，從圖中可以看出當為輸入參數DS_D，DS_D1都減小時，最大應力顯著上升，響應面為陡峭曲面。

圖7 輸入參數DS_D，DS_D1與輸出最大應力響應面

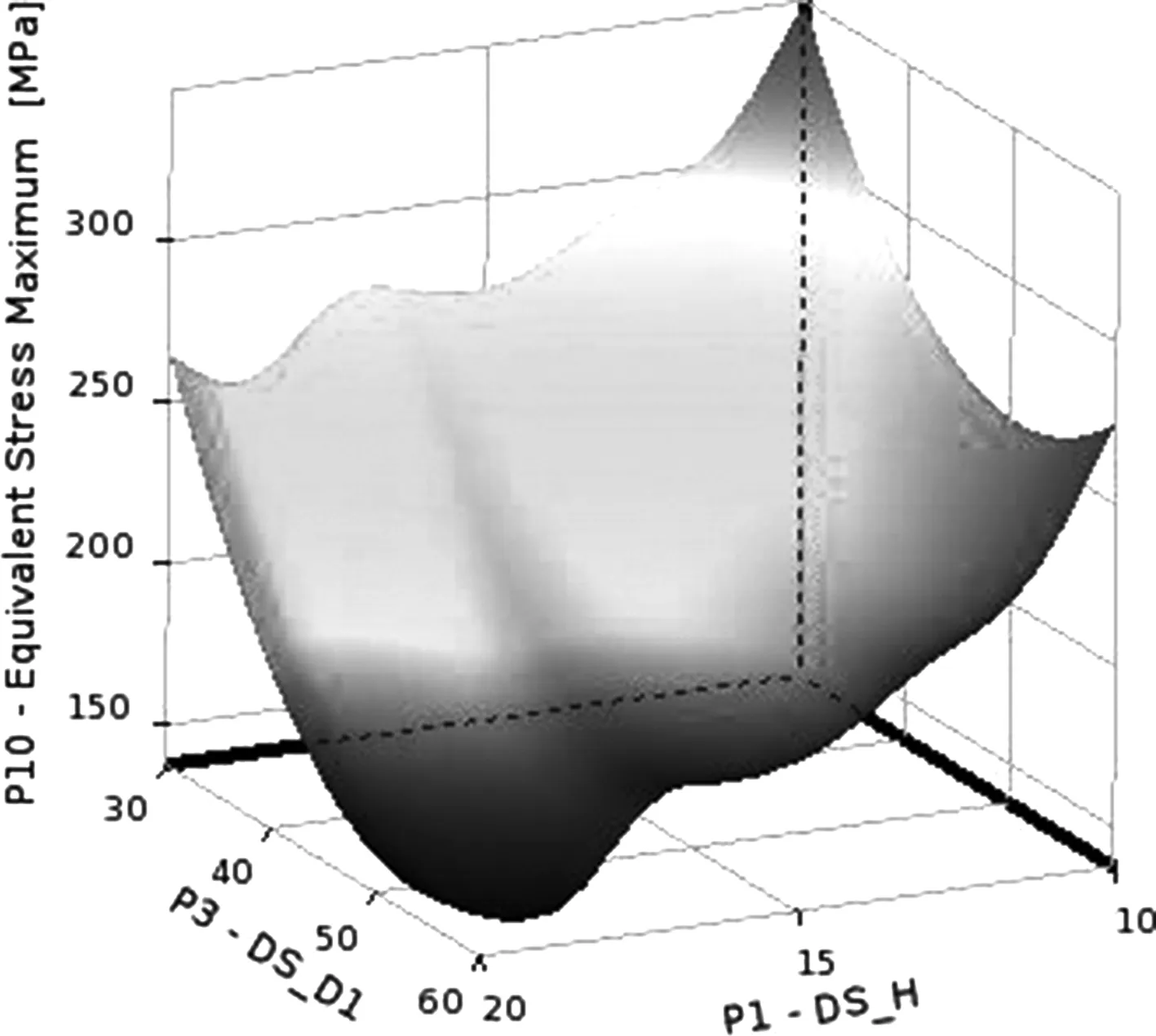
圖8 參數DS_H，DS_D與輸出最大應力響應面圖

圖8為參數DS_H，DS_D與輸出最大應力響應面，最大應力隨著輸入參數增大而迅速下降，并且存在顯著凹凸部位，在一個參數增大，而另外一個參數減小的時候，最大應力出現不同的變化，在變量區間內輸入參數對輸出最大應力貢獻度不同。

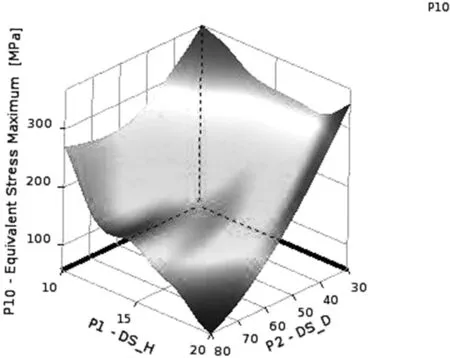
圖9 輸入參數DS_H，DS_D1與輸出最大應力響應面

圖9為DS_H，DS_D1與最大應力響應面，從圖中可知，輸入參數DS_H和DS_D1對最大應力的作用更為復雜，存在多個顯著凹凸部位，當一個輸入參數增加而另外一個參數固定時，最大應力出現非線性變化，先減小后增加。

3 拉格朗日非線性規劃算法與優化

在ANSYS軟件workbench操作平臺中提供了基于拉格朗日的非線性規劃優化算法，是一種基于梯度的單目標優化方法，其基礎為準牛頓法，可以通過設置允許的收斂殘差來提高計算準確度。設定壓縮室整體質量m為優化目標，最大應力為優化的約束條件，多參數優化數學模型如下：

(11)

設定允許殘差為10-6，迭代步數為150步，約束條件和質量目標函數如圖10和圖11所示，在迭代接近40次時候，約束與目標函數均收斂，將最優點重新作為驗證點，驗證計算結果如下表。

驗證結果表

上表中第三行為圓整后的優化參數，第四行為初始參數，質量目標下降20.3%，而最大應力下降12.5%，優化效果顯著，并且滿足許用應力條件。圖12和圖13為壓縮室輕量化前后應力分布云圖。

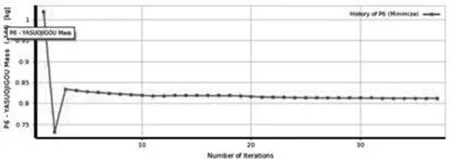
圖10 約束變化曲線

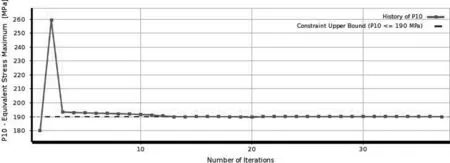
圖11 質量目標函數變化曲線

圖12 初始參數仿真云圖

圖13 輕量化后仿真云圖

結論

針對打捆機壓縮室依靠經驗設計、耗材量大等問題：

(1)建立8參數模型，以壓縮室質量為優化目標，以最大應力為優化約束條件，進行參數關聯性與敏感度分析，排除不重要參數，獲得DS_H，DS_D，DS_D1，DS_L1，DS_L2五個主要參數；

(2)通過拉丁超立方抽樣，獲得優異樣本點建立Kriging代理模型，并通過驗證點驗證模型誤差為1.26%，獲得壓縮室參數輸入與目標輸出的響應曲面；

(3)利用基于拉格朗日的非線性規劃優化算法，通過圓整輸入參數獲得最優質量目標，與初始參數相比，質量減輕20%。