k-ω SST 湍流模式三維激波分離流動修正

杜一鳴 高正紅 舒博文 邱福生,1) 宋辰星

* (沈陽航空航天大學航空宇航學院,沈陽 110136)

? (西北工業大學航空學院,西安 710072)

** (中國航發沈陽發動機研究所,沈陽 110015)

引言

基于雷諾平均N-S (Reynolds-averaged Navier-Stokes,RANS) 框架的渦黏性湍流模式(eddyviscosity model,EVM)經過40 多年的發展對于邊界層附著流動、中等壓力梯度和小分離流動以及自由剪切流動都能得到較理想的模擬結果[1-2],在廣泛的工程實踐中得到了比較充分的驗證.雖然計算機技術推動了直接數值模擬(DNS) 和大渦模擬(LES)等方法的發展,但RANS 方法被認為仍是未來幾十年工程應用中的主要模擬手段[3-4].然而由于渦黏性模式本身存在的基礎理論、模式構造和計算方法等方面的問題,導致其對于一些工程常見的分離和剪切流動難以給出滿足氣動設計需求的模擬結果[3-4].Kato 和Launder[5]就曾指出,基于傳統渦黏性假設的湍流模式實際在除了簡單剪切流動中的表現都不好.

雖然輸運方程在一定程度上體現了湍流的輸運特性,但EVM 中渦黏性系數僅采用湍流量定義的方式(即 νT=k/ω) 實際只有在湍流平衡流動中才成立[1].平衡流(equilibrium flow)[6]指的是湍動能生成與耗散達到局部平衡,且相對于對流和輸運足夠大的流動狀態.在這種流動區域中,流動狀態(例如雷諾應力等)完全由當地條件決定,而基本不存在上游歷史效應.邊界層內層就基本具有這個性質.實際上,對于滿足局部平衡的湍流,包括Prantdl 混合長度理論[7]在內的大多數湍流模式都能得到較好的模擬結果.但整個邊界層內并不完全滿足局部平衡性,即湍流非平衡流動(non-equilibrium flow),尤其是當存在逆壓梯度時,此時采用傳統EVM 的渦黏性系數定義方式就會得到比實際更大的雷諾應力預測結果,進而導致分離較小,最典型的流動就是激波?邊界層分離(shock wave-boundary layer separation).

Coakley[8]于1983 年通過修正渦黏性系數的方式首先將“雷諾應力輸運”(Reynolds-stress transport)的思想引入兩方程湍流模式.1985 年出現的Johnson-King (J-K)零方程模式[9]通過限制速度虧損律層內的主雷諾應力符合Bradshaw 假設[10-11],降低了渦黏性系數從而提高了模式逆壓梯度流動的預測能力.這種方法向方程中引入了“遲滯效應”[12],相當于考慮了雷諾應力的輸運特性.后來,Menter[13]在1992 年提出k-ω切應力輸運(shear-stresstransport,SST)兩方程模式時參考J-K 模式的處理方式引入了Bradshaw 假設,基本解決了諸如RAE2822超臨界翼型等二維激波?邊界層分離的預測問題.然而對于較強的三維激波?邊界層分離流動,目前的EVM 均無法進行正確模擬,其激波和分離預測位置向上游移動,嚴重偏離實驗結果.以較為經典的ONERA M6 機翼[14]為例,跨聲速α=6.06°狀態下激波相比于小攻角狀態更強,同時展向更大范圍內都存在邊界層分離,包括k-ωSST 和Spalart-Allmaras(S-A)[15]模式在內的EVM 都無法得到合理的計算結果[4].近年來的計算分析[4,16-19]表明,采用雷諾應力模式(Reynolds-stress model,RSM)才能夠對上述工況進行較準確的預測.RSM 直接求解各雷諾應力分量的輸運方程,不存在雷諾應力各向同性和非平衡流動模擬問題[19].但此類二階封閉模式建模難度較大,且目前數值穩定性和收斂性仍未達到工程應用的水平[3-4].

由于湍流非平衡流動的復雜性,目前針對渦黏性模式這一問題的研究較少,尚未形成廣泛有效的修正策略.Li 等[20-21]的研究具有代表性,他們在開發渦黏性湍流模式結冰翼分離模擬能力時也考慮了非平衡性的影響,并以湍動能生成和耗散之比作為開關參數針對ω方程的耗散項進行了修正,取得了較好的改進效果,但并未進行激波分離流動方面的驗證討論.Rumsey 和Vatsa[22]針對ONERA M6 機翼α=5.06°和α=6.06°狀態對包括J-K 零方程模式和S-A 一方程模式在內的幾種湍流模式進行了網格和格式耗散的收斂性研究,發現采用耗散較大的數值方法(例如矢通量分裂格式FVS)以及稀網格能夠得到收斂且與實驗吻合較好的計算結果.一旦降低數值格式耗散水平或加密網格,計算就會得到不穩定的大分離,激波位置大幅向前緣移動.Frink[23]采用S-A 模式在稀網格上也得到了ONERA M6 機翼α=6.06°狀態y/b=90%截面較好的壓力分布模擬結果,但他認為這只是“某種巧合”,因為由稀網格引入的截斷誤差還很大,同時“翼尖附近復雜的流動結構可能已經超過了S-A 模式的模擬能力”.然而上述研究并未對EVM 三維激波?邊界層分離模擬失效的具體原因作出分析.

從機理角度出發,實際上,對于由逆壓梯度導致的邊界層分離流動,邊界層內的雷諾應力水平基本決定了其抵抗逆壓梯度的能力以及分離流動的特性,因此湍流模式對雷諾應力的求解直接影響其激波-邊界層分離流動的模擬精度.在渦黏性假設的框架下,雷諾應力本構關系和渦黏性系數定義方式就是兩個突破點.

以目前較常用的k-ωSST 兩方程湍流模式為修正對象,首先通過典型二維和三維算例對模式的激波?邊界層分離模擬能力進行評估,分析三維激波?邊界層分離的物理特性和模式失效機理,并討論現有非線性雷諾應力本構關系對于此類問題的改進效果.在此基礎上,提出兩種針對渦黏性系數的修正方法,并通過與原始模式和RSM 的雷諾應力特性對比、網格收斂性分析等確認修正方法進行三維激波?邊界層分離模擬的合理性和有效性.

1 模擬能力評估

1.1 k-ω SST 模式與Bradshaw 假設

相比于k-ε模式,k-ω模式更適合邊界層流動模擬,對逆壓梯度主導的附著流動和小分離流動有較高的模擬精度,但對湍流變量的遠場邊界條件比較敏感[1].Menter[13]基于k-ω模式和k-ε模式各自的特點,巧妙地將兩種模式相融合,并在邊界層內外通過開關函數(blending/switch function)進行切換.直接將兩種模式形式和參數進行混合的稱為基準模式(baseline model,BSL).Menter 認為EVM 與RSM 的主要區別在于EVM 僅考慮了湍動能和耗散率的輸運特性,而未直接考慮雷諾應力本身的輸運效應.而對于非平衡流動,渦黏性系數的定義缺陷將導致雷諾應力不再符合其輸運特性,進而得到更大的雷諾應力預測結果,使分離預測偏小.針對這一問題,k-ωSST 模式在BSL 模式的基礎上引入了Bradshaw 假設(不可壓縮形式)[10-11]

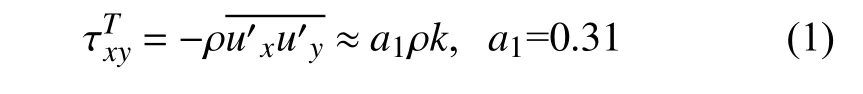
即對于邊界層、尾跡和混合層流動,主雷諾應力分量與湍動能k的比值為常數.實驗測量表明,常數a1基本保持在0.3 左右,稱為Bradshaw 常數[10]或Townsend 常數[11].Bradshaw 假設被公認能夠較準確地反映主雷諾應力分量在對數律層和速度虧損律層(尾跡區)中的特征.根據湍流邊界層分層結構,對數律層和速度虧損律層是受勢流區壓力梯度影響最大的區域,通常湍流模式在對數律層的表現對于準確預測中等壓力梯度流動非常重要,而模式對于邊界層尾跡(速度虧損律層)的預測精度決定了模式對強逆壓梯度流動的預測能力[1,24].

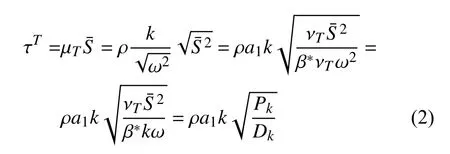
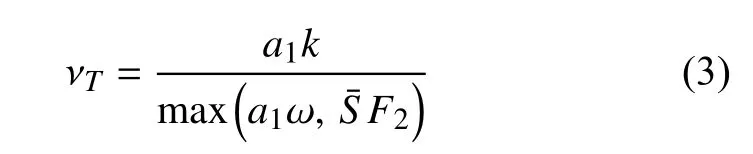
當湍動能生成項大于耗散項時有Sˉ >a1ω,上式就會保證雷諾應力不超過 ρa1k.其中,開關函數F2用于限制Bradshaw 假設僅在邊界層和尾跡內起作用.相比之下,k-ωBSL 模式僅采用 νT=k/ω 的原始定義方式.加入如式(3)的渦黏性系數限制后,相當于強制雷諾應力在逆壓梯度下滿足Bradshaw假設,此時雷諾應力不會被過度預測,能夠顯著提升模式的二維激波?邊界層分離模擬能力.圖1 給出了采用不同湍流模式及圖2 網格(y+<2)[25]得到的RAE2822超臨界翼型[26]Ma=0.75,Re=6.2 × 106,α=2.72°(AGARD Case 10)狀態[27-28]激波?邊界層分離的計算壓力系數和摩擦系數(下表面Cf取相反數)對比.可以發現,SST 模式與RSM 計算結果基本一致,激波位置和強度與實驗數據吻合較好,BSL 模式模擬的激波位置靠后,且分離泡較小.

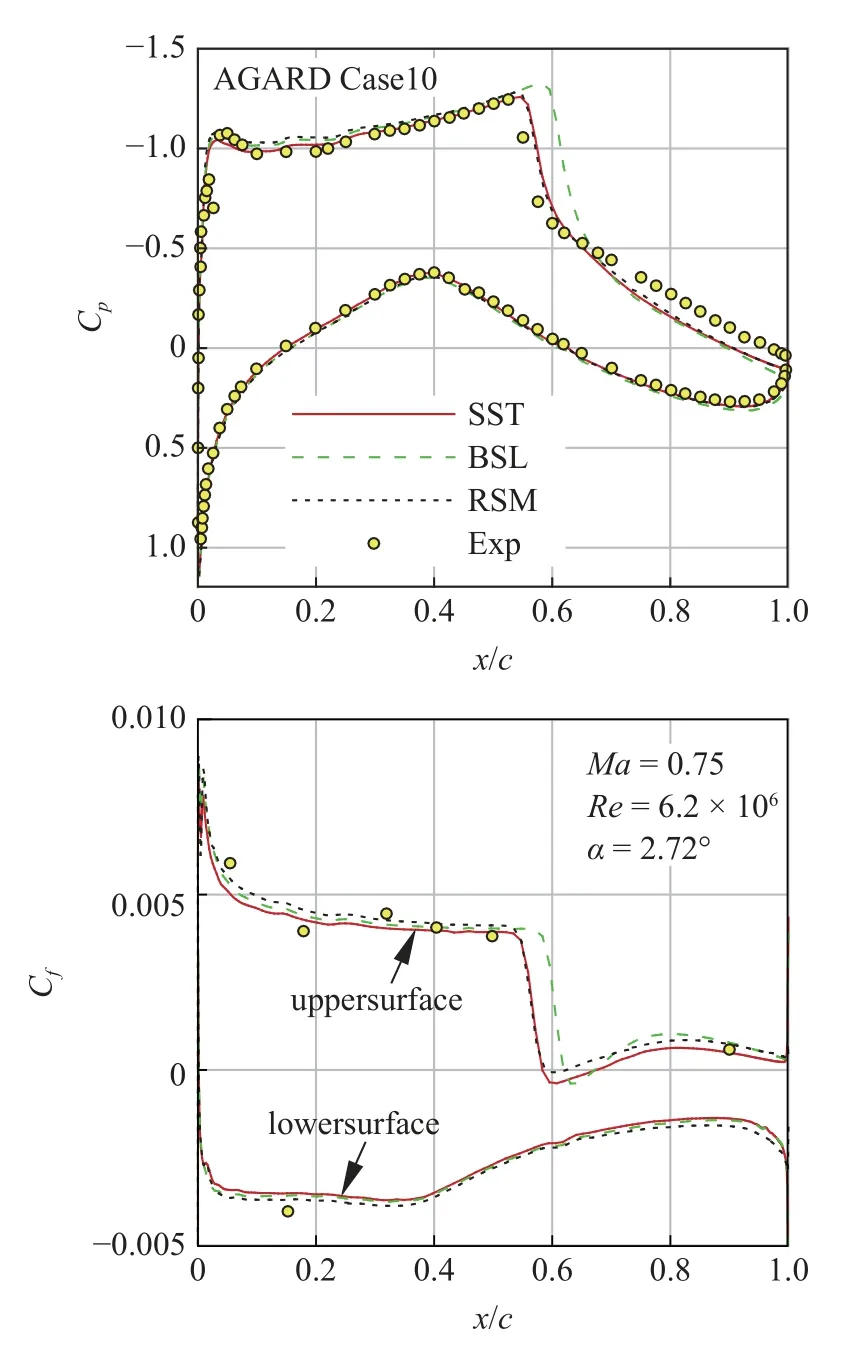
圖1 計算壓力系數和摩擦系數分布與實驗的對比Fig.1 Comparison of computed pressure and skin friction coefficients distribution with experiment

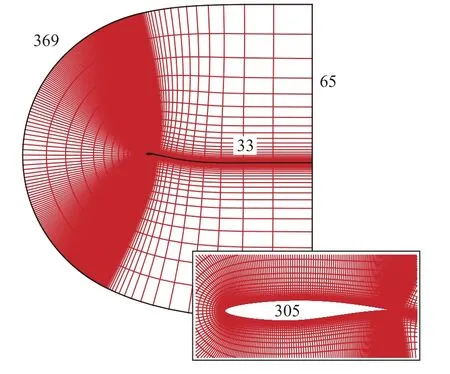
圖2 RAE2822 翼型計算網格Fig.2 Computational grid of RAE2822 airfoil

本文RANS 計算均采用NASA CFL3 D 結構化網格求解器[27]完成.該求解器在有限體積框架下求解三維可壓縮非定常RANS 方程,有多種湍流模式可供選擇,計算效率和計算精度滿足工程應用需求.所采用的k-ωSST 模式為2003 年Menter 等[29]提出的改進版本.此外,RSM 計算結果將用作對比分析,采用的是Togiti 和Eisfeld[30]于2015 年提出的SSG/LRR-g模式,其中g≡ (1/ω)1/2為長度尺度相關量.

1.2 三維激波-邊界層分離算例驗證

ONERA M6 機翼[14](圖3)包含了復雜的激波?邊界層分離流動特征,同時外形簡單且實驗數據比較完善,是CFD 研究的經典算例.其中Ma=0.84,α=3.06°狀態對應附著流動,機翼上表面的λ 形激波結構是其主要特征.隨著攻角的增加,上表面分離區逐漸增大,當α=6.06°時,外翼段分離已經非常明顯.本文選取的計算狀態在表1 中給出.計算網格規模為510 萬(圖4,y +≈ 1).

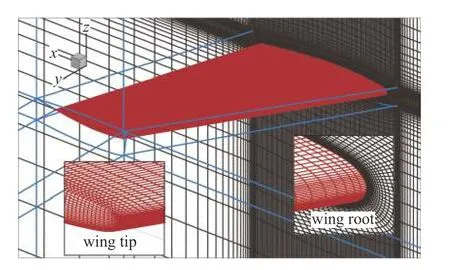
圖4 ONERA M6 計算網格Fig.4 Computational grid of ONERA M6 wing

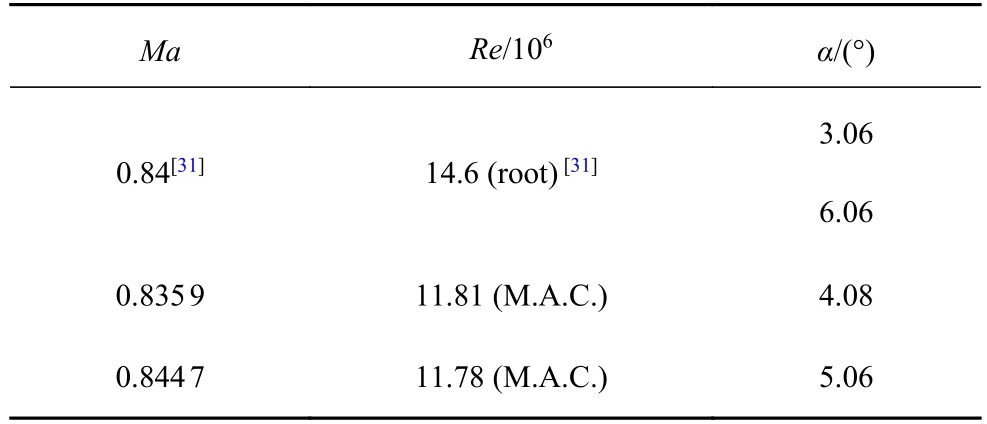
表1 ONERA M6 機翼計算狀態Table 1 Computation conditions of ONERA M6 wing

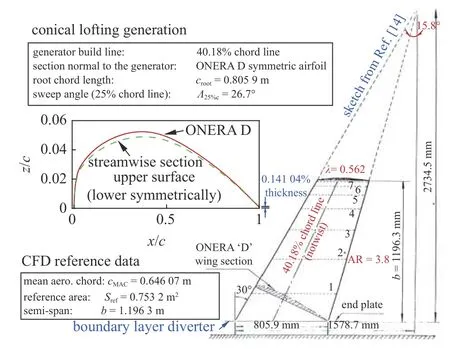
圖3 ONERA M6 機翼形狀與模式參數Fig.3 Shape and parameter of ONERA M6 wing

圖5 給出了ONERA M6 機翼α=3.06°和α=4.08°狀態(分別對應原始實驗Case 2308 和Case 2563)典型截面計算壓力分布與實驗的對比.可以看出,對于分離不強的小攻角流動狀態,k-ωSST 模式具有比較理想的預測精度,計算結果與實驗吻合很好,且與BSL 模式和RSM 的計算結果差別較小.

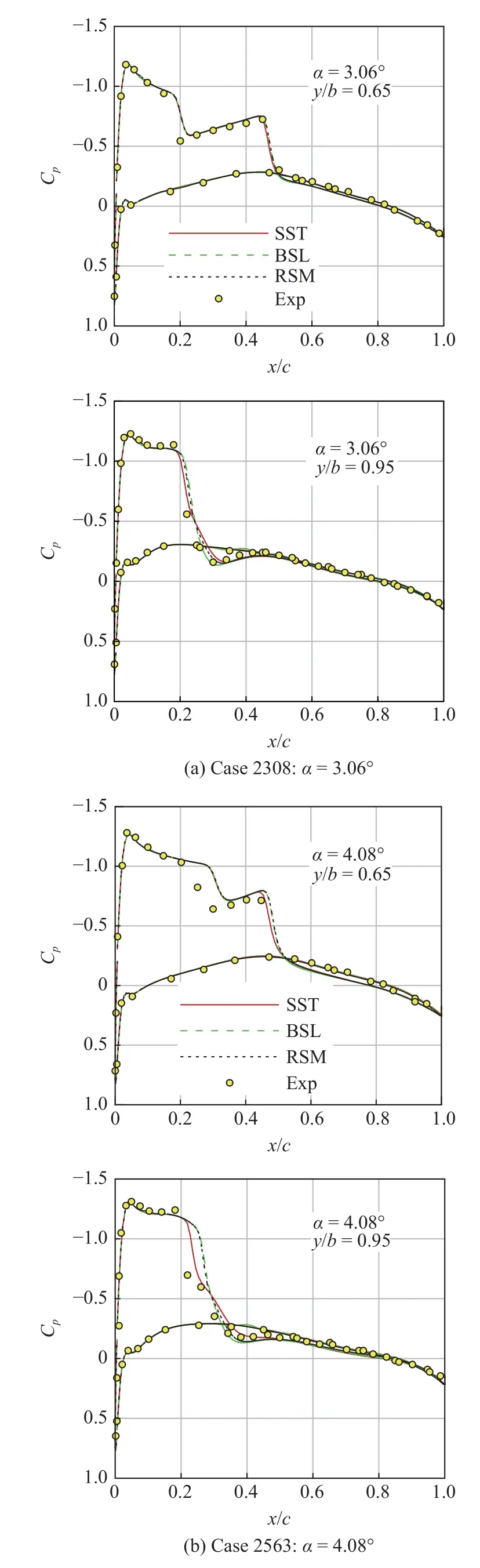
圖5 小攻角狀態計算壓力分布與實驗的對比Fig.5 Comparison of computed pressure distribution with experiment at small angles of attack

然而,對于更大攻角下的強激波?大分離流動,目前大多數渦黏性模式都無法勝任.圖6 和圖7 給出了α=6.06°狀態不同湍流模式計算的上表面流動形態及典型截面壓力分布.可以發現,k-ωSST 模式得到的激波位置從y/b=65%開始大幅向前緣移動,與RSM 的計算結果和實驗結果的偏離程度不斷增大[17,23].在α=5.06°狀態下,這種情況發生在y/b=80%之后[23].

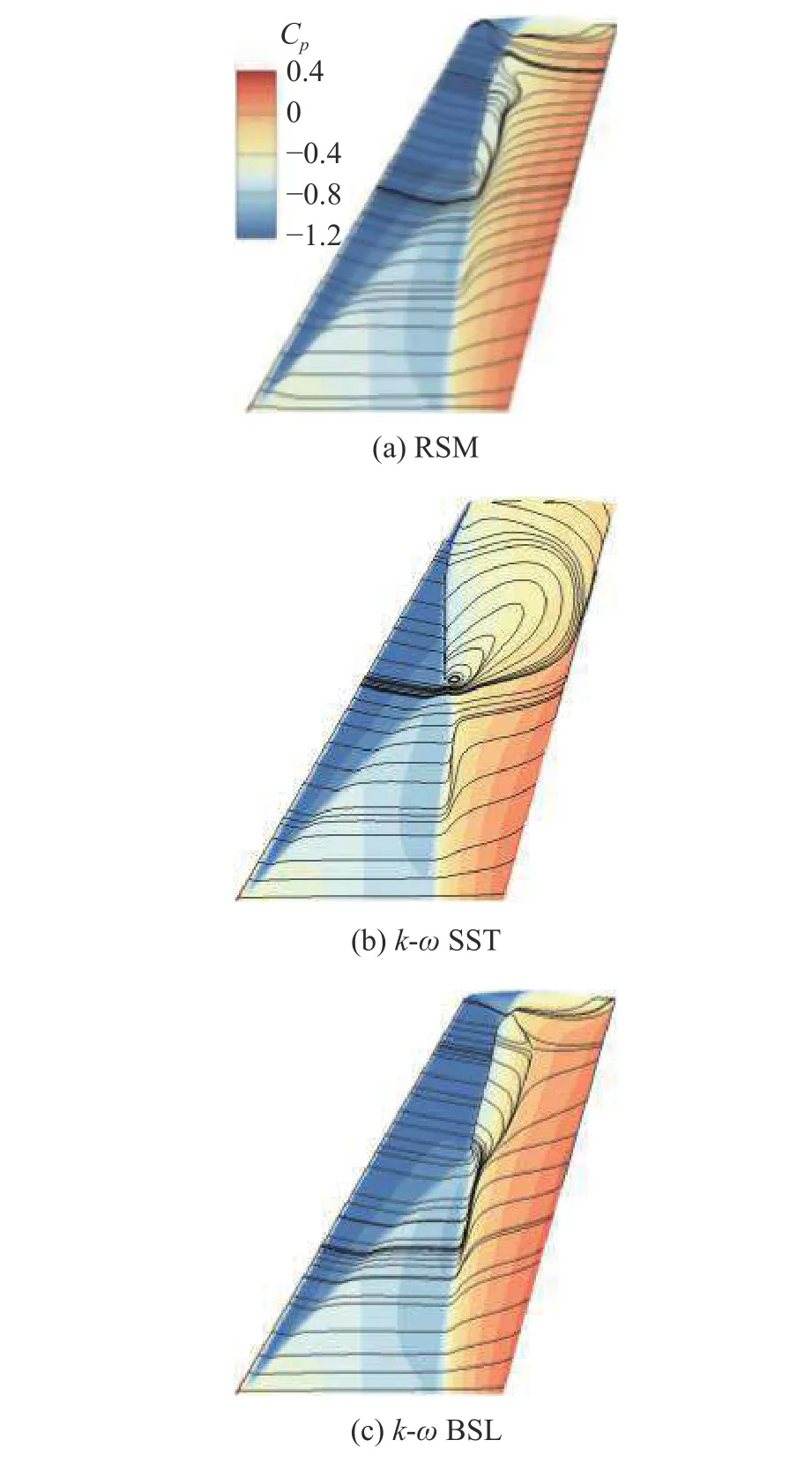
圖6 表面壓力分布與極限流線對比Fig.6 Comparison of surface pressure distribution and limited streamline pattern

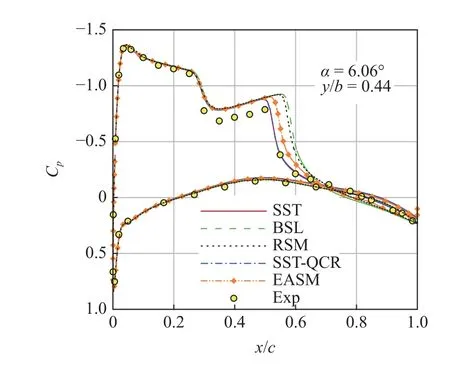
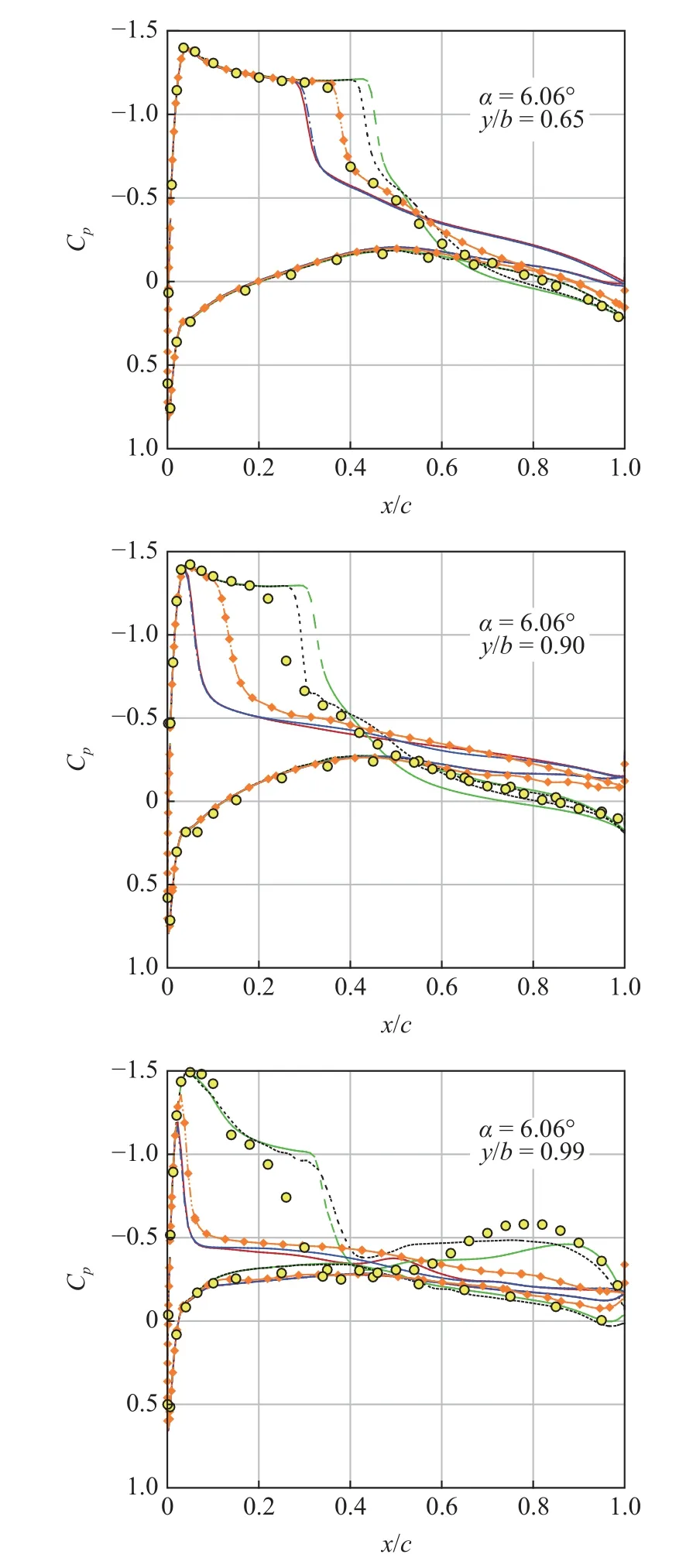
圖7 α=6.06°狀態計算壓力分布與實驗的對比(非線性模式與RSM、SST 和BSL 模式)Fig.7 Comparison of computed pressure distribution with experiment at α=6.06° (nonlinear models with RSM,SST and BSL models)

2 失效機理分析

為進一步確認造成渦黏性湍流模式三維激波?邊界層分離模擬失效的原因,對RSM 和k-ωSST 兩種模式進行網格收斂性分析,自研網格序列包括微量網格(T,網格量0.74 百萬)、稀網格(C,網格量1.35 百萬)、中等網格(M,網格量3.3 百萬)、密網格(F,網格量5.1 百萬,圖4)和特密網格(EF,網格量11.0 百萬);物面法向首層網格高度均為y +≈ 1,這參考了Frink[23]的研究發現,即法向網格密度相比于表面網格密度對結果的影響很小.從圖8 中可以發現,RSM 在所有截面都表現出了較好的網格收斂趨勢,激波模擬結果隨網格加密逐漸陡峭且更加接近實驗結果(但在EF 網格上收斂性較差,未完成計算).對于k-ωSST 模式,內翼段(y/b<65%)也表現出了正常的網格收斂趨勢,但在外翼段卻表現出隨著網格加密激波位置前移、逐漸偏離實驗結果的趨勢,這與Rumsey 和Vatsa[22]的結論一致.稀網格的計算結果也表明,某些看似正確的數值模擬結果其實是具有誤導性的,因為“實際上整個計算的截斷誤差還未通過加密網格或降低數值格式耗散得到充分降低”[22].考慮到外翼段激波位置即是分離點,造成上述預測失準的一種合理解釋是:外翼段激波?邊界層分離流動本身是由分離主導的,對于傳統EVM,雷諾應力預測偏小導致分離靠前;分離后物面壓力恢復嚴重受阻進而導致激波的產生,也即分離點直接決定了激波位置.因此,正確預測三維激波?邊界層分離的關鍵首先在于正確的雷諾應力求解,而非網格或數值格式.而雷諾應力求解又依賴模式的建模方法,具體來說就是雷諾應力和渦黏性系數的定義.

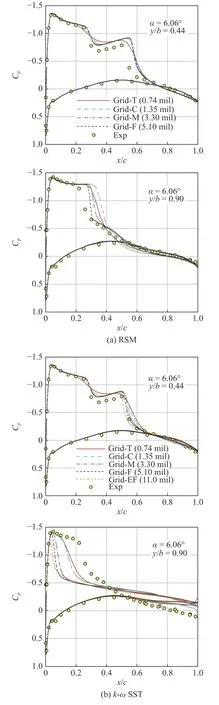
圖8 α=6.06°狀態網格收斂性對比Fig.8 Comparison of grid convergence at α=6.06°

從雷諾應力定義的角度考慮,基于渦黏性假設的線性雷諾應力本構關系是雷諾應力求解的基礎.完整的不可壓縮流動雷諾應力本構關系(constitutive relation)具有如下形式

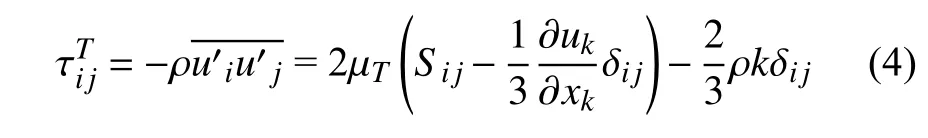
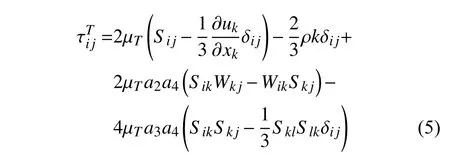
計算穩定性和精度較好.為了發展更簡潔魯棒的方法,Spalart[35]于2000 年針對SA 模式提出了“二次本構關系”(quadratic constitutive relation,QCR)方法,在線性雷諾應力本構關系的基礎上增加了非線性項,即

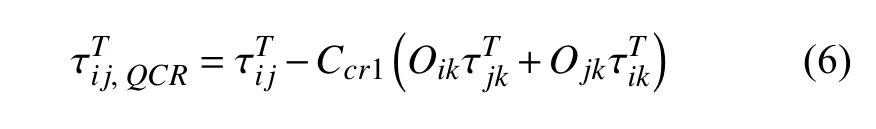
對各向異性流動模擬有明顯改善,原理上適用于所有渦黏性模式.上述變量定義可參見文獻[34-35].由于S-A 模式本身不求解湍動能,在使用渦黏性假設時無法計入其中的湍動能項(即式(4)第三項).于是,2013 年Mani 等[36]針對S-A-QCR 方法引入了湍動能項的近似計算方法.2020 年Rumsey 等[37]通過近似項系數調整進一步改進了原始S-A-QCR修正方法.而基于湍動能方程的兩方程模式能夠直接求解湍動能,因此在構造k-ωSST-QCR 方法時,后來加入的湍動能近似項可以不必考慮,直接采用原始形式的雷諾應力本構關系式(4)即可.

分別采用Rumsey-Gatskik-ωEASM 和k-ωSST-QCR 方法對ONERA M6 機翼α=6.06°狀態進行模擬,計算結果見圖7.可以發現,k-ωEASM 雖然起到了一定延緩分離的作用,但這種作用靠近外翼段逐漸消失,翼尖附近的計算結果與線性模式基本相同.而k-ωQCR 方法在該算例中基本未表現出明顯效果.從式(5)和式(6)的構造形式可以看出,非線性雷諾應力本構關系考慮的是流動中旋轉、剪切等引起的非線性效應,因此適用于模擬雷諾應力各向異性主導的流動(特別是二次流動),也能夠提升分離流動中雷諾應力分量的計算精度[38],但對于改善湍流非平衡流動模擬能力并沒有實質作用.

3 修正方法構造

根據上述分析和討論,本節從渦黏性系數的定義角度出發,分別基于Bradshaw 假設和湍流長度尺度提出兩種針對k-ωSST 模式的三維激波?邊界層分離模擬修正方法.

3.1 基于Bradshaw 假設的修正方法

從圖6 和圖7 的對比結果看,未考慮Bradshaw假設的BSL 模式反而得到了與RSM 接近的表面壓力分布和分離狀態,在分離明顯的外翼段截面壓力分布也與實驗接近.由于Bradshaw 假設是利用Klebanoff 零壓力梯度平板邊界層試驗數據[10]提出的,因此只針對附著流動適用;隨后的研究表明,其在弱逆壓梯度和小分離流動中也基本可用[39],但可能不適用于其他流動狀態[24].本文的一種合理的推斷是,在三維強逆壓梯度作用下,各雷諾應力分量的量級接近,因此Bradshaw 假設成立的基礎——“主雷諾應力分量”的概念不復存在(即標量近似形式不再適用),此時不能再假設僅有某個分量是主要的而忽略其他分量的作用.多個量級相當的雷諾應力分量會使Bradshaw 假設對雷諾應力的限制(式(1))不再準確(過度限制了雷諾應力的生成),導致SST 模式在三維較強的激波分離流動中預測雷諾應力嚴重不足,造成分離和激波位置靠前.但從圖7 還可以看出,BSL 模式在外翼段的模擬精度并不高,同時對于分離再附后的壓力分布計算精度較差,因此單純通過屏蔽Bradshaw 假設并不能解決問題,但嘗試對Bradshaw 假設進行相應修正不乏是一種可行措施.

針對高超聲速中的激波?邊界層干擾(shock wave-boundary layer interaction,SWBLI)模擬,近些年已有一些針對Bradshaw 假設的修正嘗試.Georgiadis 等[39-40]對Bradshaw 常數a1的實驗和理論基礎進行了研究,并嘗試提高常數a1至0.34,0.355 甚至0.37,對多個超聲速SWBLI 問題進行了模擬.結果表明,這種方式對提高SWBLI 問題模擬精度很有幫助.文獻[41]在針對SWBLI 問題的湍流模式不確定性分析中,也將常數a1的取樣范圍定為了0.31～ 0.40.根據Bradshaw 假設的作用機理,提高a1的目的在于放寬對雷諾應力生成的限制,進而提高雷諾應力水平并推遲分離.

通過測試對比,將Bradshaw 常數a1調整為0.355 并對ONERA M6 機翼α=6.06°狀態進行模擬,計算結果如圖9 和圖10 所示.可以發現,采用Bradshaw假設修正方法(記為“SST-a1=0.355”)得到的截面壓力分布與RSM 接近,同時與實驗數據相比,修正方法在外翼段(即y/b=90%,95%及99%截面)得到了精度優于RSM 和BSL 模式的激波模擬結果,此外激波?分離再附后壓力分布的模擬準確性也與RSM 相當,且相比于BSL 模式,與實驗數據更加吻合.需要說明的是,由于Bradshaw 假設是一種基于實驗觀測的半經驗關系式,直接對其進行經驗化修正是否符合物理需要進一步考慮.

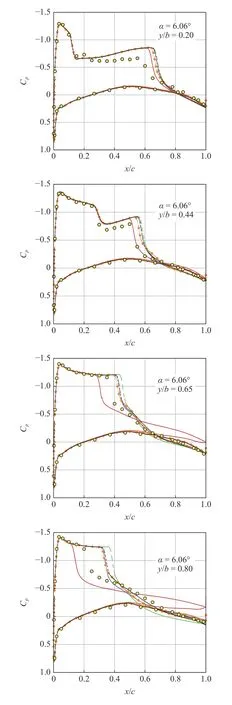
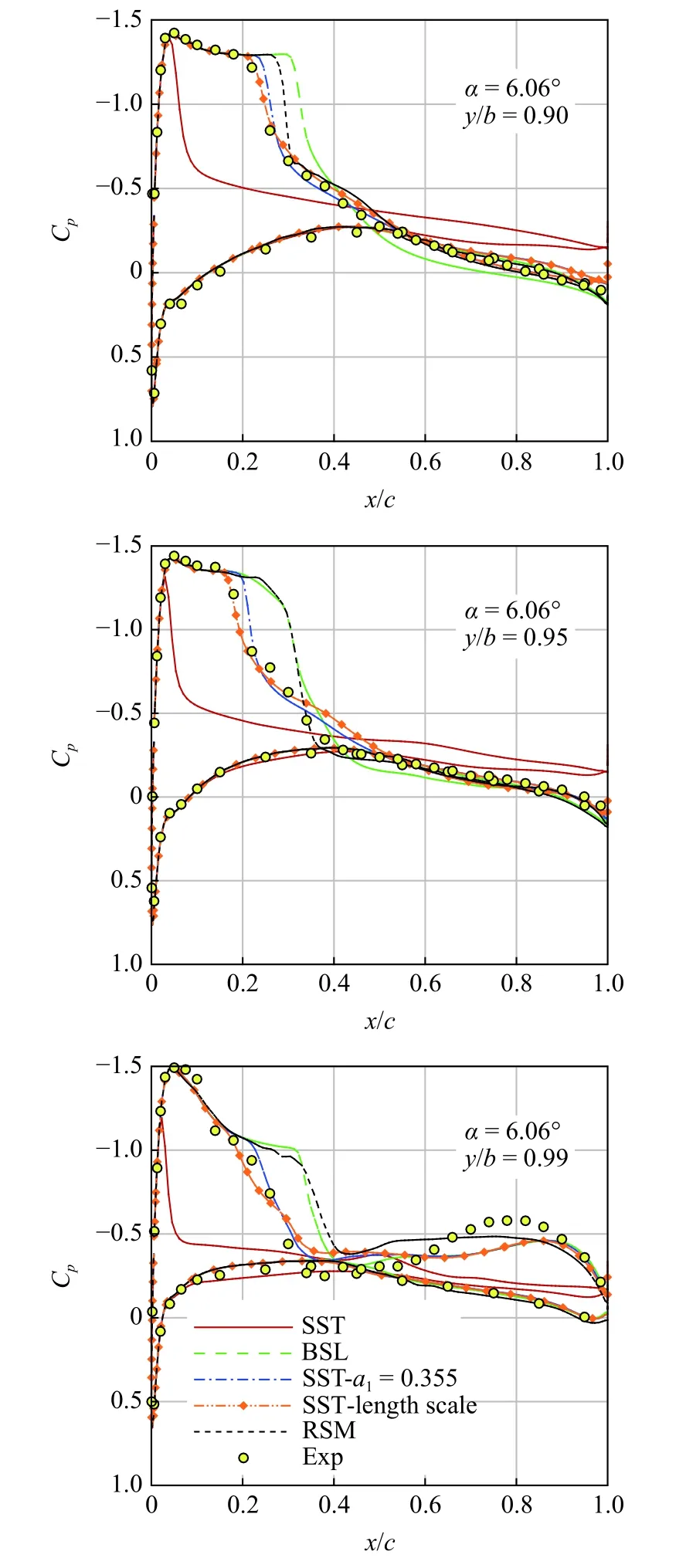
圖9 α=6.06°狀態計算壓力分布與實驗的對比(修正方法與RSM、SST 和BSL 模式對比)Fig.9 Comparison of computed pressure distribution with experiment at α=6.06° (correction methods with RSM,SST and BSL models)

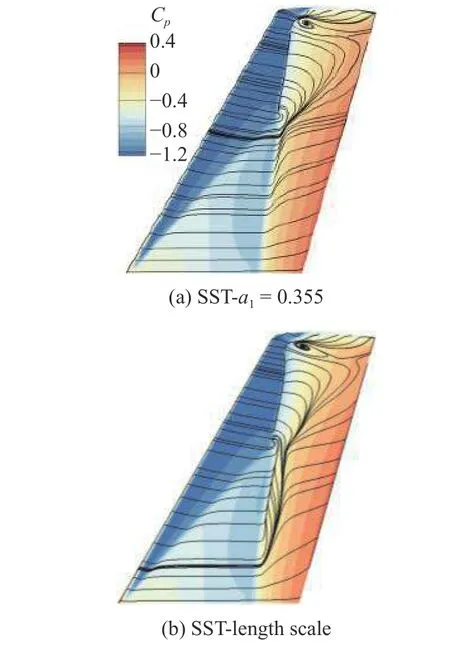
圖10 表面壓力分布與極限流線對比(修正方法)Fig.10 Comparison of surface pressure distribution and limited streamline pattern (correction methods)

3.2 基于湍流長度尺度的修正方法

無論是RANS 方法還是LES、DNS 方法,尺度與能量的關系都是最重要的理論基礎.從機理角度看,湍流的(特征)長度尺度對應湍流邊界層的大尺度結構,支配湍流邊界層的特性;同時尺度也是湍流能量的另一種體現,根據湍流渦拉伸和能量級聯理論,尺度越大則能量也越大.RANS 湍流建模實際都可歸結到對湍流長度尺度的建模問題上.但RANS方法并不存在解析尺度,因此在湍流模式中,長度尺度實際是一種“平均尺度”的概念.對于k-ω模式,假設ω和渦黏性系數 νT都是湍動能k的函數,根據量綱分析有

式中C為常數.可以發現,長度尺度l是通過湍流單位耗散率ω定義的(Wilcox 稱ω方程為“尺度決定方程”(scale determining equation)[8],即單位耗散率ω為湍流長度尺度相關量),ω方程決定了建模尺度也就決定了模式所能預測的湍動能(雷諾應力)大小.換句話說,誰(湍流模式)能夠更精準地對湍流特征長度尺度進行建模,誰就能更準確地把握湍流的主要特征,得到更理想的模擬結果.針對激波?邊界層分離模擬問題,可以考慮對ω方程進行修正,進而提高渦黏性系數和雷諾應力的建模精度.很多湍流模式的問題如旋轉/曲率問題等[38]也都是以此為出發點進行定位、分析和修正的.

針對長度尺度最著名的研究當屬混合長度理論[7].該理論雖因未考慮流動歷史效應已經很少使用,但其對湍流大尺度的研究和目前的RANS 湍流/轉捩建模方法具有指導意義.Prandtl 類比分子動理論,認為湍流脈動速度(類比于分子熱運動的平均速度)應大致取決于當地的平均速度梯度與流體微元跳動距離(類比于分子自由程長度)的乘積,例如對于二維平行剪切流,沿y向跳動的流體微團具有如下形式的脈動速度

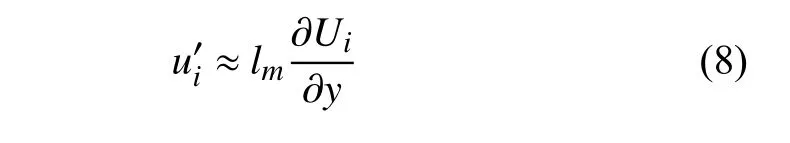
其中lm稱為混合長度,它相當于流體微元的拉格朗日自由程,這個距離小于平均流動變化的尺度(即在這個距離內跳動基本不喪失其原有速度),從概念上講可以將它視為對湍流大尺度的一種度量.隨后,馮·卡門和Van Driest 相繼提出并完善了混合長度的計算方式[33],其中馮·卡門提出湍流邊界層中當地脈動長度尺度基本與壁面距離成正比(由于壁面對于湍流脈動起限制作用),即

其中κ稱為卡門常數,約等于0.41.這說明湍流大尺度主要集中在遠離壁面的邊界層對數律層(對數率層中黏性效應也基本可以忽略)和速度虧損率層,這也正是上文提到的邊界層內受壓力梯度影響最大的區域,應該作為修正對象.Kolmogorov[42]稱l為“external (length) scale of turbulence”,其中的“external” 指的就是邊界層外層.

根據上文的分析,原始湍流模式在三維激波-邊界層分離流動中雷諾應力預測不足,即渦黏性系數或湍動能預測偏小,應提高建模尺度.由于單位耗散率ω與長度尺度l成反比(式(7)),為了提高建模長度尺度應該考慮降低ω;而降低ω最直接的方式就是增大ω方程的耗散項,這也是旋轉/曲率修正等采用的思路.根據上文的討論,對于強逆壓梯度下的非平衡流動,湍動能的生成與耗散不再相當,因此兩者之比是比較合適的指標函數,即

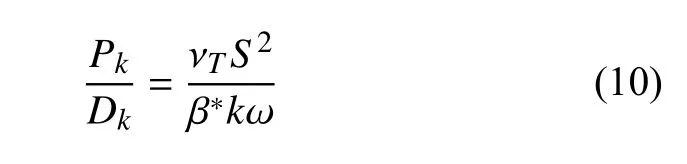
然而并不能在湍動能生成項一旦大于耗散項時就啟動修正,畢竟兩者在附著流動和弱逆壓梯度下的比值也并不是一直相等的,因此需要對上述比值設置一個開啟閾值,相當于在逆壓梯度大于一定程度時才進行修正.根據Menter[13]的研究,湍動能生成率與耗散率的最大比值即便在復雜剪切層中也僅在2 左右.通過對不同攻角下ONERA M6 機翼流動的測試并與RSM 對比,發現該閾值取為1.5 能夠基本滿足預測需求.故構造如下形式的ω方程耗散項修正函數

縱觀三季度的冰箱線上市場，三門、多門、對開門冰箱呈現出不同幅度的增長，以多門勢頭最盛，漲幅高達61.9%；而線下除多門冰箱有7.5%的增長外，其他品類均出現不同程度的下跌。總體來看，多門冰箱表現搶眼，已成為消費者的主流選擇，且上升趨勢十分明顯；對開門冰箱上升勢頭有所放緩，但依然是不少消費者的最終選擇；三門冰箱以高性價比也獲得了越來越多的線上客戶青睞，但在對消費體驗要求更高的線下市場，已經少有昔日風光；兩門冰箱則逐漸式微，尤其在線下市場，消費者的目光更容易被中高端產品吸引。

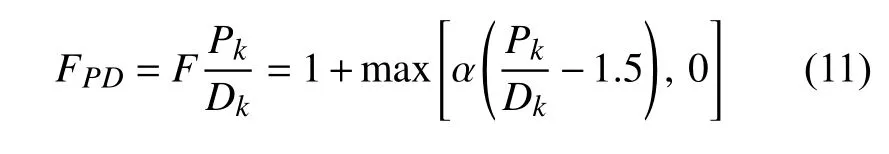
其中α的作用類似一個放大系數,即在Pk/Dk大于1.5 后控制修正量的大小.修正系數FPD與原始ω方程的耗散項相乘就得到新的耗散項

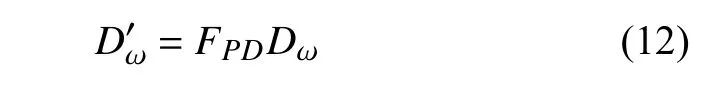
采用上述修正方法對ONERA M6 機翼α=6.06°狀態進行模擬可以得到如圖11 所示的結果.以外翼段RSM 計算結果為參照,放大系數α經過測試取為4 較為合適.圖12 給出了采用上述修正方法得到的y/b=90%截面湍動能生成與耗散之比云圖,可以發現在翼型前緣上游的大部分區域兩者之比均大于2.壓力分布及局部Pk/Dk云圖顯示(圖13),前緣上游沿流向存在較大范圍逆壓梯度,Pk/Dk很快增大至2 以上,這也是跨聲速翼型/機翼流動較為明顯的特征,同時也是非平衡性修正發揮作用的主要區域[21].由圖13 前緣附近云圖可以看出,Pk/Dk在壁面附近很快下降至1 左右;而在分離之前,從邊界層中間位置(對數律層)開始,Pk/Dk又開始增長并在分離之前達到2 以上,此時修正方法也會發揮作用.可以發現,若將上述開啟閾值(目前為1.5)減小,則修正將在前緣及分離前更上游的位置開啟,使得ω降低、建模尺度提高的區域增大,進而造成雷諾應力增大,分離和激波位置將后移.與原始k-ωSST 模式模擬結果相比(圖11),加入FPD修正項后推遲了外翼段的分離,計算精度基本與RSM 相當.但相比于Bradshaw 假設修正方法(即“SST-a1=0.355”)的計算結果,FPD使得湍動能增長過度,激波和分離位置被大大推后,同時分離再附后壓力分布模擬結果并不理想.分析造成上述結果的原因:雖然采用湍動能生成項與耗散項之比能夠識別前緣附近及邊界層內非平衡性的增長,但這仍然沒有考慮到長度尺度的實際建模不準問題.也就是說,“湍動能生成項與耗散項之比大于1.5”只是依據計算結果的判斷,此時計算結果是否準確、建模長度尺度是否足夠還應該進行判斷,以決定是否開啟FPD.這就需要對長度尺度進行量化.

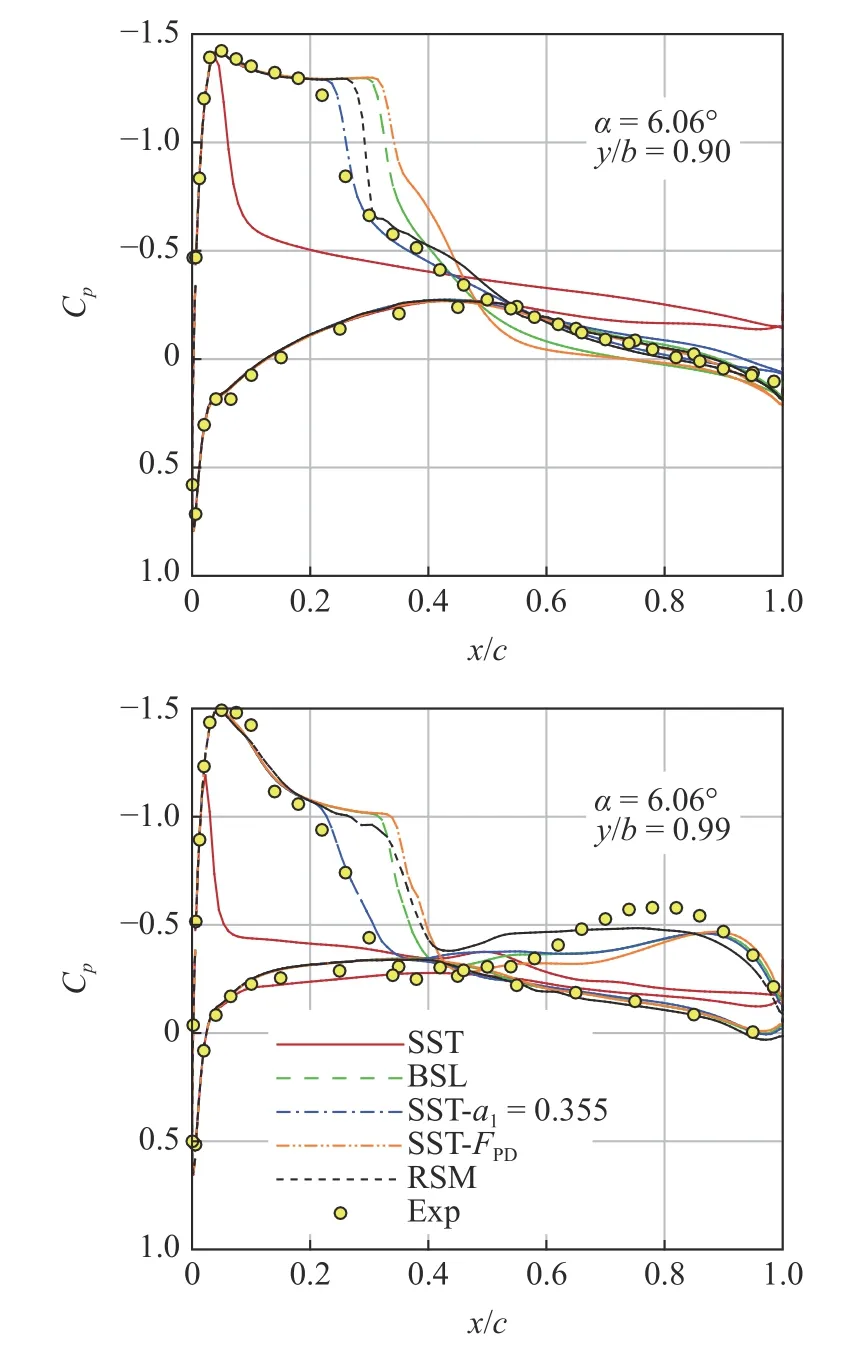
圖11 采用FPD 修正的壓力分布與其他結果的對比Fig.11 Comparison of FPD-fixed pressure distribution with other results

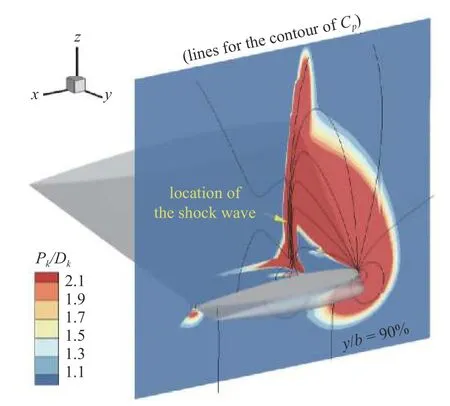
圖12 采用FPD 修正的截面湍動能生成/耗散之比Fig.12 Sectional contour of Pk/Dk using FPD correction

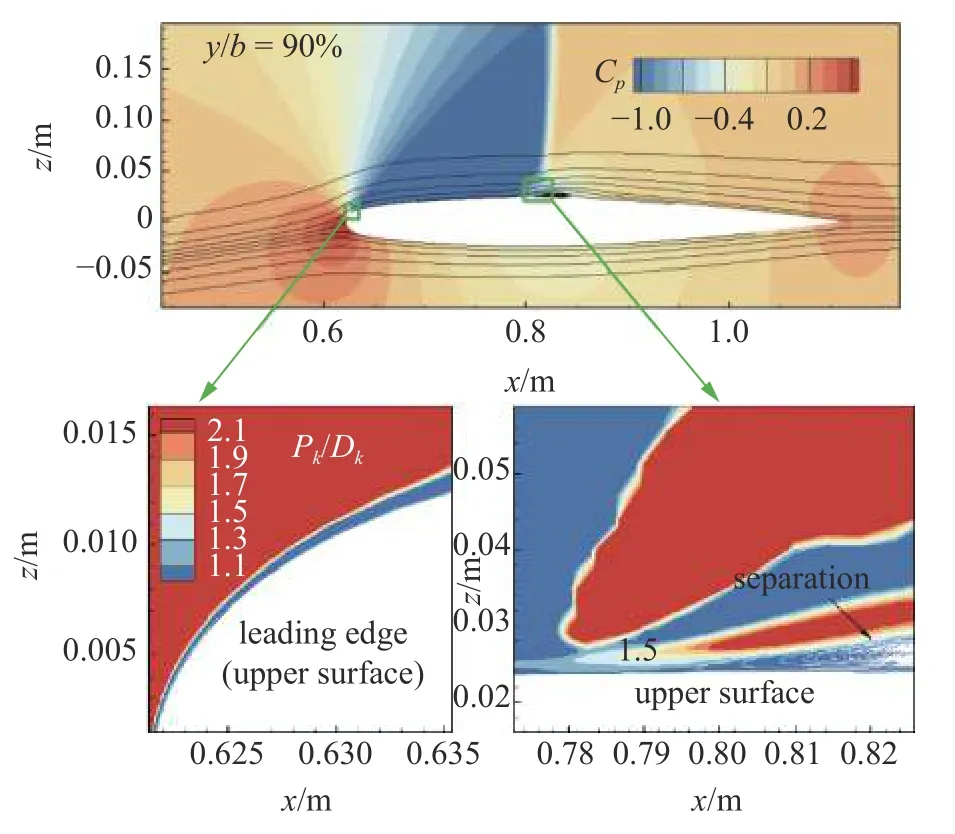
圖13 y/b=90%截面前緣及分離前湍動能生成/耗散之比Fig.13 Pk/Dk contour at leading edge and before separation of y/b=90% section

在S-A 模式[15]的建模過程中,利用了一個長度尺度的比例定義,即

其中,y為最近壁面的距離,為S-A 模式中定義的一個量,它等于渦量加上一個修正項.數值計算表明,在對數律層r≈ 1,向更外層發展這個數值開始減少,在更內層由于 νT很小,這個值逐漸接近于0.可以從雷諾應力的角度理解r的變化.由于壁面的阻尼作用,雷諾應力在壁面附近(黏性底層)幾乎為0,而在黏性底層之上雷諾應力和渦黏性系數 νT將快速增大,并在對數律層某處達到最大,此時分子黏性的作用基本可以忽略.因此可以認為對數律層所包含的長度尺度和能量是最大的,而 νT可以作為衡量尺度變化的變量.根據量綱分析,可以采用應變不變量或渦量進行量綱調整,若采用S-A模式定義的,就會得到一個具有長度量綱的量,即.同時上文已經指出,混合長度lm=κy也可以作為湍流邊界層大尺度的度量,因此在對數律層附近兩者應近似相等,即

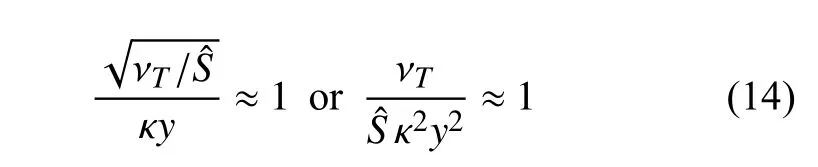
但由于是采用計算值定義的,而混合長度lm=κy在計算網格確定時就已經確定了,因此式(14) 可以理解為“計算”長度尺度(分子) 與“應有”長度尺度(分母 κy)的比.如果建模及計算的渦黏性系數不足,則上式中的計算“長度尺度”就會小于“應有長度尺度”,比例系數r不再等于1.因此可以利用這個關系,當r小于某個值后才開啟式(12)中的FPD項.采用QCR 方法[35]中用于歸一化的參考量(下式根號項)代替,最終得到的比例系數為

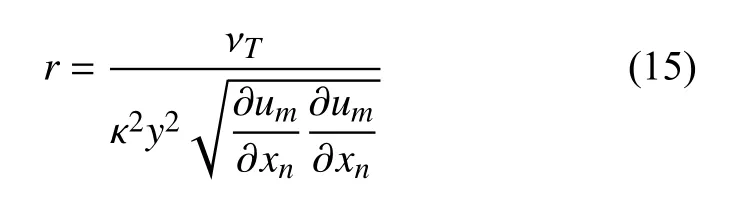
借鑒粗糙壁面修正中Hellsten-Laine 開關函數[43]的形式構造“長度尺度開關函數”,采用雙曲正切函數對是否開啟FPD進行控制

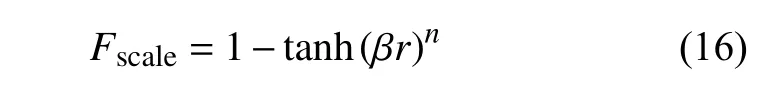
其中系數β和n是類比Hellsten-Laine 開關函數[43]引入的:β的作用可以理解為當長度尺度比例系數r小于1/β時開啟FPD(此時tanh 項接近于0,Fscale≈1),而冪指數n的作用在于使Fscale在r=1/β左右進行0-1 快速切換.于是新的修正函數FPD為

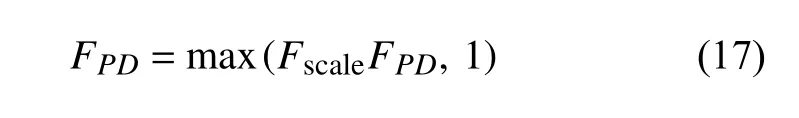
與1 相比取最大值的操作意味著不存在耗散項的減小.以ONERA M6 機翼α=6.06°狀態外翼段RSM 計算結果為參照,通過測試將系數β和n分別取為9 和3.圖14 給出了不同修正方式下的y/b=90%截面湍流量云圖,可以發現,經過Fscale限制后的FPD(式(17))較未限制時(式(11))對單位耗散率的抑制作用減弱,分離位置更靠前.

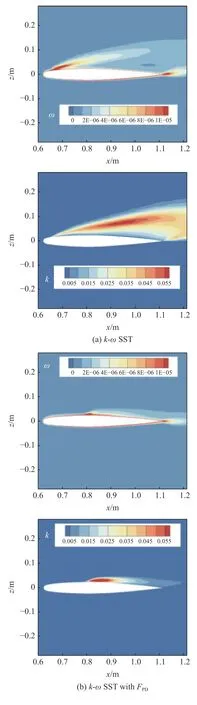
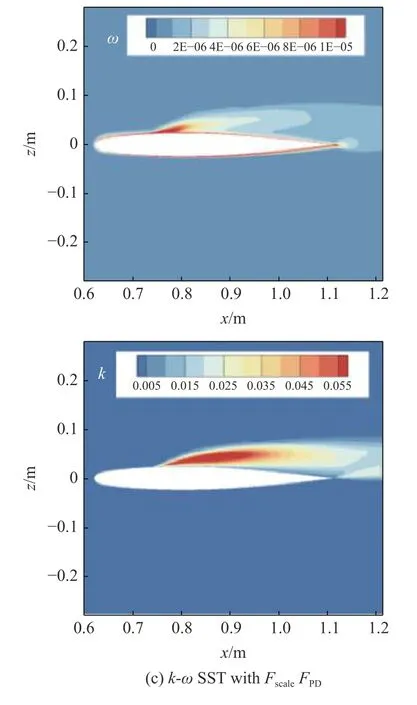
圖14 對修正函數FPD 進行限制前后的湍流量計算結果對比Fig.14 Comparison of the computed turbulence variables before and after limiting the modified function FPD

圖9 中也顯示了采用長度尺度修正方法(記為“SST-length scale”)得到的截面壓力分布,可以發現,length scale 修正方法與Bradshaw 假設修正方法得到的結果比較接近,初步證明了所提出的兩種修正方法的有效性.

圖10 進一步給出了兩種修正方法計算的表面流動形態,其中壓力分布接近.不同的是,兩種修正方法得到的外翼段分離區較RSM 的預測結果更大(RSM 外翼段有明顯的分離再附),且length scale 修正方法在內翼段第二道激波處也預測到了一定的分離再附流動,這些現象是否存在還需要實驗等方法的進一步驗證.

4 驗證與討論

4.1 網格收斂性分析

上文的網格收斂性分析已表明,ONERA M6 機翼大攻角流動是由分離主導的,無法準確求解是由于k-ωSST 模式未能準確描述流動的主要特性,這一點無法通過網格加密或提高格式精度彌補.采用所提出的兩種修正方法后(圖15),外翼段表現出了合理的網格收斂特性(即隨著網格加密,激波分辨率提高),表明兩種修正方法均能正確反映該問題的流動特征,截斷誤差能夠隨網格加密不斷減小,這進一步驗證了兩種修正方法的合理性.從圖15 中還可以看出,length scale 修正方法對表面網格密度的敏感性較低,稀網格規模就能基本滿足模擬精度要求.

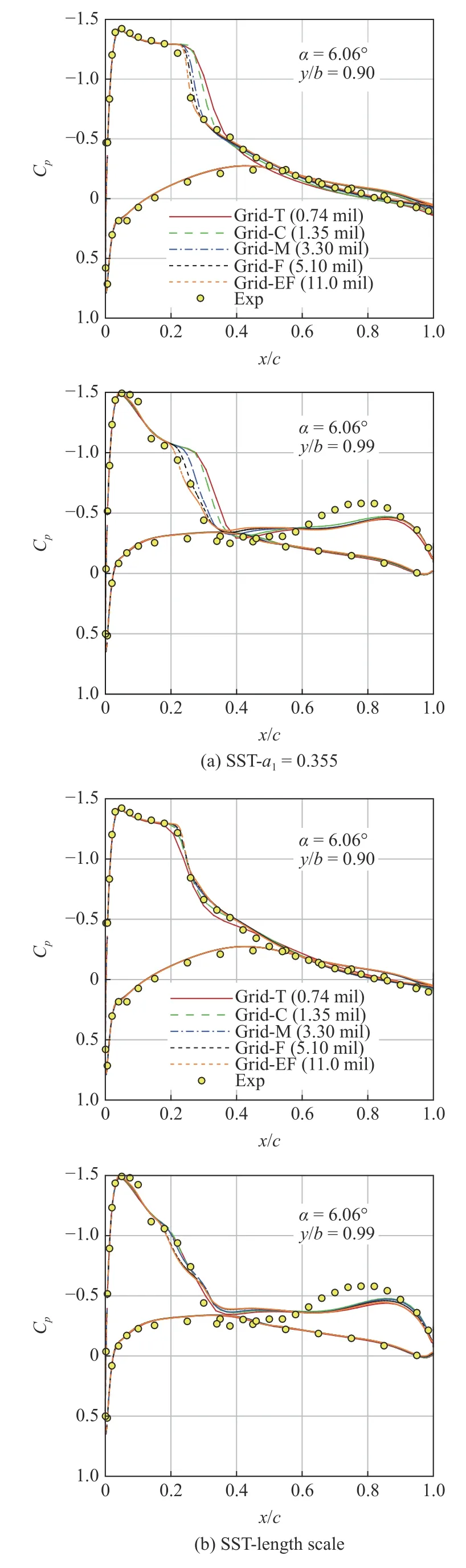
圖15 α=6.06°狀態兩種修正方法的網格收斂性對比Fig.15 Grid convergence comparison of two corrections at α=6.06°

4.2 其他攻角狀態驗證

為了進一步確認兩種修正模擬方法的正確性,對ONERA M6 機翼另外兩個攻角狀態進行數值模擬,典型截面的計算結果如圖16 所示.可以看出,α=4.08°狀態各個模式和修正方法的模擬結果接近;而對于α=5.06°狀態,兩種修正模擬方法的計算結果與RSM 基本相同,相比于原始模式改進明顯.

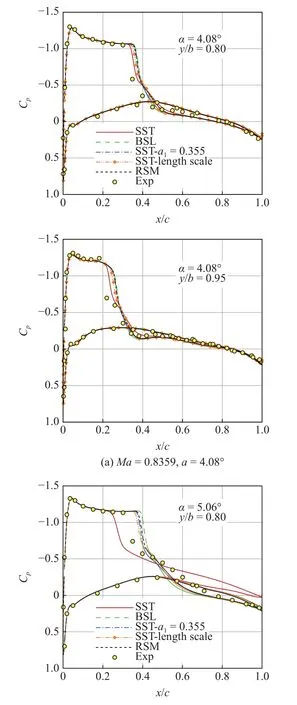
圖16 兩種修正方法應用于其他攻角狀態的計算壓力分布對比Fig.16 Computed pressure distribution comparison of two corrections at other angles of attack

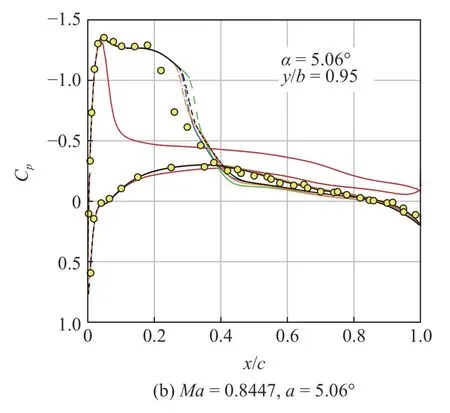
圖16 兩種修正方法應用于其他攻角狀態的計算壓力分布對比(續)Fig.16 Computed pressure distribution comparison of two corrections at other angles of attack (continued)

4.3 雷諾應力特性分析

下面分析三維激波?邊界層分離流動的雷諾應力特性.圖17(a)為采用DNS 方法計算的三維零壓力梯度湍流平板邊界層雷諾應力分布,其中u,v,w分別代表流向、法向和展向速度.可以發現,近壁區雷諾應力分量之間存在比較明顯的差異,其中流向雷諾正應力和流向?法向雷諾切應力明顯大于其余應力分量,這時主雷諾應力這一概念是成立的.圖17(b)為ONERA M6 機翼α=6.06°狀態y/b=90%站位前緣x/c=8%處邊界層內的雷諾應力分布.由于原始SST 模式預測的分離非常靠前,已經覆蓋了該位置,因此雷諾應力分量都很大(點劃線).以Bradshaw 假設修正方法(虛線)為例,與RSM (實線)計算的雷諾應力分布對比可以發現,法向和展向雷諾正應力的相對大小較平板邊界層明顯增大,特別是展向雷諾正應力增長明顯;同時,除流向?法向切應力外,其余兩個切應力分量也增長明顯,三者基本具有相同量級,均不能被忽略.這也證明了在三維激波?邊界層分離流動中,主雷諾應力分量并不唯一,對各向雷諾正應力和切應力都需要進行比較準確(量級至少要正確)的評估才能最終得到正確的分離和壓力分布計算結果.

從圖17 中還可以發現,Bradshaw 假設修正方法得到的雷諾應力分量之間的相對大小與RSM 的計算結果是一致的,但絕對大小還是有區別的.整體來看,與RSM 相比,渦黏性模式修正方法計算的雷諾正應力較大,切應力較小.

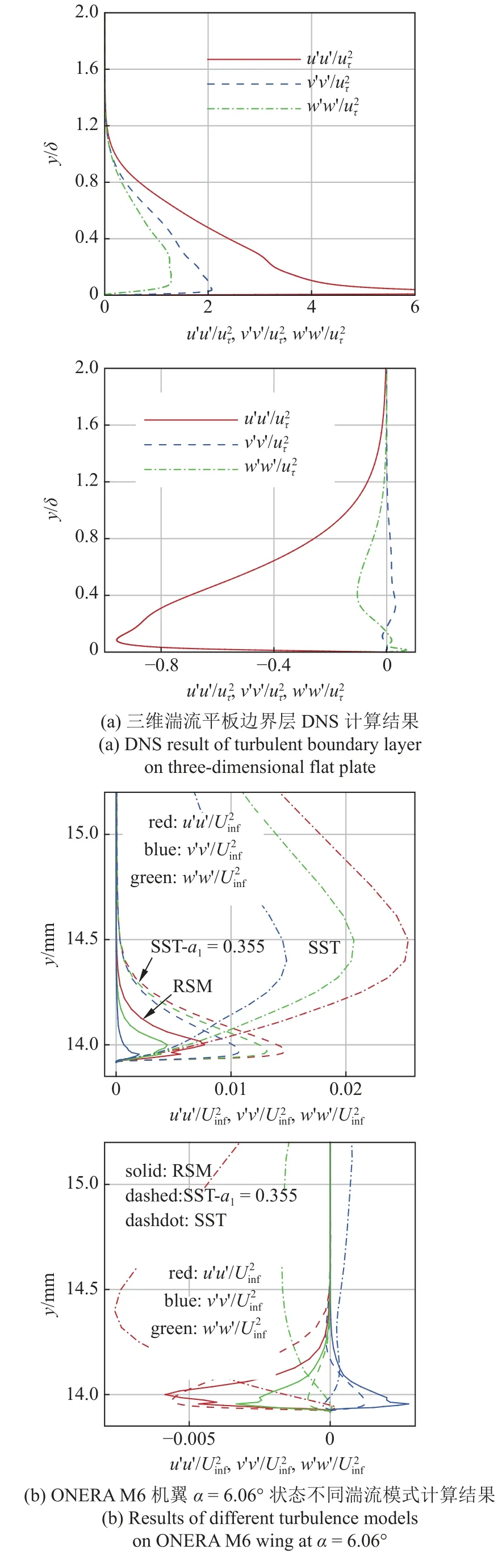
圖17 不同流動中雷諾應力分量的對比Fig.17 Comparison of Reynolds-stress component for different flows

4.4 湍流平板邊界層壁面律驗證

最后,對湍流平板邊界層進行確認計算,驗證上述修正方法是否會對附著流動模擬造成影響.參考Wieghardt 等[44]湍流平板實驗的參數和數據,計算網格及邊界條件如圖18 所示.圖19 給出了不同方法得到的壁面律曲線與實驗結果及光滑平板湍流邊界層壁面律理論曲線的對比.可以發現,原始k-ωSST 模式及兩種修正方法在線性底層和對數律層均得到了一致且與實驗和理論曲線吻合的計算結果,說明修正方法并未對模式原有的附著流動模擬能力造成不利影響,具有一定的通用性.

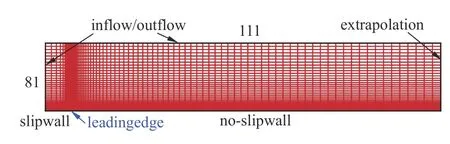
圖18 湍流平板邊界層計算網格Fig.18 Computational grid of turbulent boundary layer of flat plate

圖19 不同方法的壁面律曲線與實驗數據和理論值的對比Fig.19 Computational wall-function law by different methods comparing with experimental and theoretical data

5 結論

針對常用渦黏性湍流模式在三維激波分離流動中的模擬能力不足,基于k-ωSST 模式提出了兩種修正方法,均取得了滿意的改進效果,為渦黏性湍流模式應用于工程中的此類流動提供了思路.本文主要結論如下.

(1)渦黏性湍流模式中的渦黏性系數定義方式不適用于非平衡流動,k-ωSST 模式為此引入的Bradshaw 假設考慮了雷諾應力的輸運特性,使模式具備了較好的二維激波分離流動模擬能力.

(2)三維激波分離流動不存在主雷諾應力分量(存在多個量級相當的雷諾應力分量),使得Bradshaw假設限制了雷諾應力的生成從而失效.同時,目前已有的非線性雷諾應力本構關系并不能從本質上提高模擬能力,原因是非線性修正主要針對旋轉、剪切引起的二次效應.

(3)基于提高Bradshaw 常數和基于長度尺度的修正方法均使k-ωSST 模式表現出了合理的網格收斂特性(其中后者的網格敏感性較低),對于ONERA M6 機翼大攻角狀態和其他攻角狀態也能夠進行準確模擬,驗證了本文修正方法的合理性和有效性.

由于本文針對三維激波分離流動提出的修正方法與k-ωSST 模式引入Bradshaw 假設的初衷相反,因此兩種修正方法應用于二維激波分離流動會得到稍向后移的激波分離位置.這涉及到方法的二維/三維適用性問題,需要對修正函數等進行更細節的考慮.此外,由于長度尺度修正方法的模式化、經驗化意味更強,本文所給定的修正參數的通用性還有待進一步驗證和改進.最后,若處理更高馬赫數的問題,壓縮性修正也是需要考慮的問題.