剪力滯效應下箱型梁的可靠度分析

周月娥， 劉泰玉， 嚴鵬

(廣西民族大學建筑工程學院， 南寧 530006)

箱型梁具有良好的結構性能，在工程中有著廣泛的應用。箱型梁進行隨機分析和可靠度分析在實踐中需要考慮一些不確定因素。可以對箱型梁進行隨機分析的方法有蒙特卡洛有限元法[1]、響應面法[2]和隨機有限元等方法。蒙特卡洛有限元法在抽樣模擬次數增加的條件下，計算結果接近實際解，因此常作為其它結構隨機分析方法的比較基準。但是，需用大量的計算時間來獲得一個有效的計算分析結果。響應面法分析時所需樣本點少、計算量適中、與確定性結構分析解耦。然而，由于事先不可預知驗算點，需要每次迭代得到樣本點來保證響應面與真實極限狀態曲面在驗算點附近較為接近。攝動隨機有限元法[3]不用樣本實驗和統計數據分析，對隨機場的信息處理技術要求比較低，只需知道隨機參數的前兩階矩就可以得到比較好的結果。現有的薄壁結構設計研究分析中可用的是一次二階矩法[4]，對其進行可靠度計算的數值分析方法較少，在處理復雜問題時存在一些困難。考慮了工程中的不確定因素后，通過在標準正態空間中尋找最近原點，可以間接得到結構的可靠度指標[5]。尋找這個點的計算方法是一個不斷迭代程序[6]，需要通過計算極限狀態函數值和它在每一步相對于基本隨機變量的梯度，求解梯度可以選擇使用隨機有限元法[7]或者有限差分法[8]。

現有的箱型梁確定性元分析中梁單元節點位移中都含有剪力滯函數[9-11]，并且沒有考慮箱梁參數的隨機性。文獻[12-13]建立的箱型梁剪力滯效應分析方法中，用附加撓度及其一階導數代替剪力滯函數，克服了采用剪力滯函數所建立方法的缺陷。為此，結合基于附加撓度建立的箱型梁有限元分析方法和攝動隨機有限元法建立一種可以對箱梁結構求解可靠度指標的迭代求解方法，主要是通過處理可以尋找標準正態空間中離坐標原點最近點時極限狀態函數對隨機變量的梯度。選取原變量空間中的均值點為初始迭代點，分別基于驗算點和均值點迭代求解極限狀態函數的梯度，即可得到結構的可靠指標。通過兩種方法對箱型梁進行分析，可以考慮參數隨機性對箱梁可靠度計算的影響，也可以對比分析兩種方法的適用范圍。

1 箱型梁隨機分析的攝動隨機有限元法

圖1、圖2所示的左端固定右端自由的箱型梁，翼緣橫截面的縱向位移函數u(x,y)由箱梁撓度w(x)和附加撓度wa(x)確定[12]。

圖1 承受外荷載作用的箱型梁簡圖

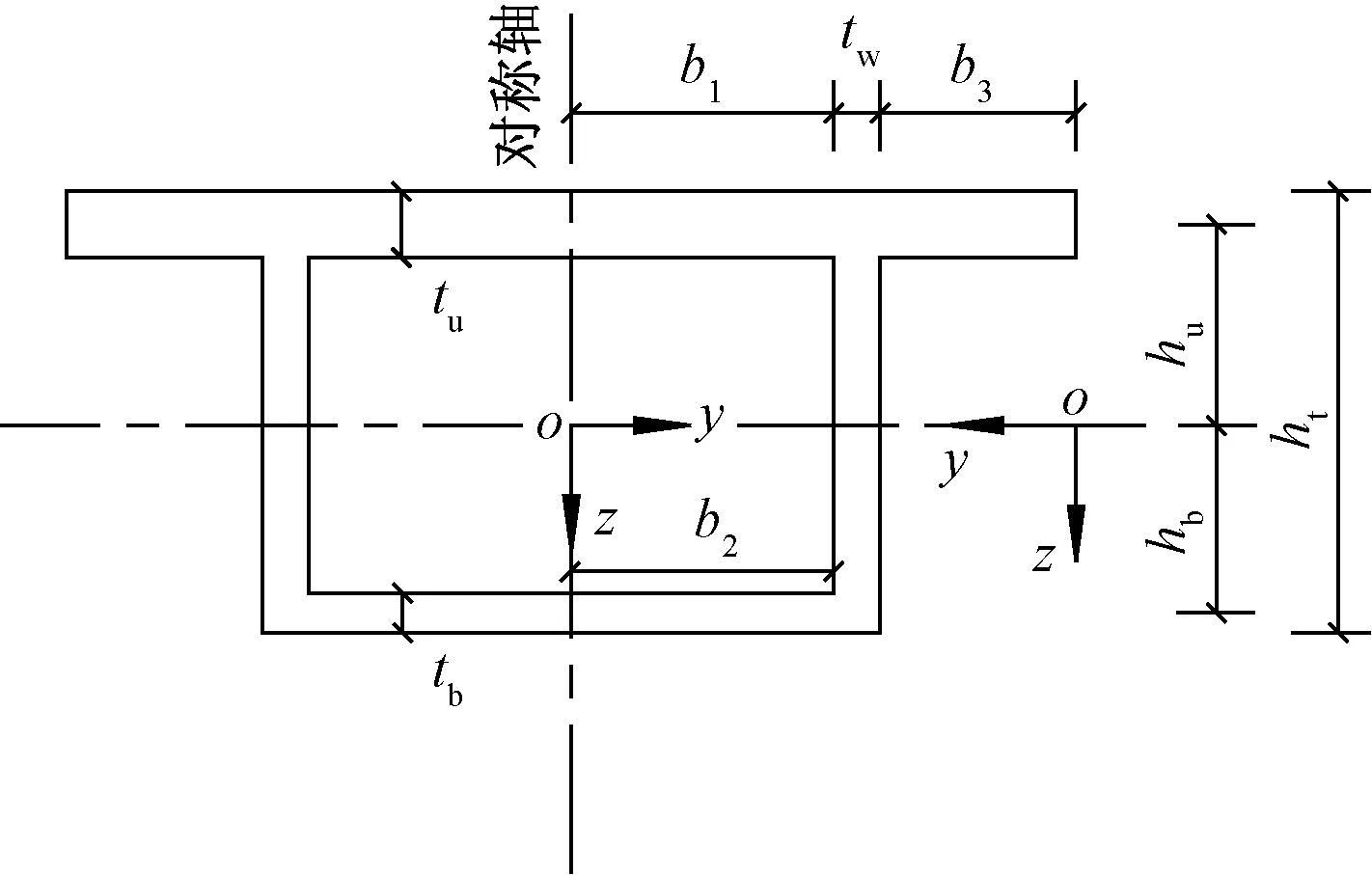
圖2 箱型梁橫截面尺寸

(1)

式(1)中：h為翼板到箱型梁截面形心的距離；b可取b1、b2和b3，分別為箱梁截面兩腹板之間上、下翼板寬度1/2及懸出翼板的寬度；I為箱梁整個截面的模量；Is為箱梁上下翼板的模量,且有

I=Is+Iw

(2)

(3)

式(3)中：m2=b2/b1;m3=b3/b1。

在分布荷載q(x)作用下，利用式(1)定義的位移函數，建立箱梁的總勢能泛函，可表示為[12]

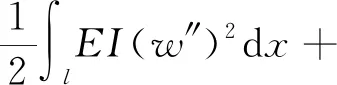
(4)

式(4)中：l為箱型梁的長度；E為彈性模量；G為剪切模量。

當箱型梁邊界條件不同時,式(4)定義的箱型梁總勢能泛函中有關撓度w(x)和附加撓度wa(x)的表達式是不同的。根據箱型梁的一維離散有限元法[13]，總勢能泛函用矩陣形式表示為

(5)

式(5)中：

(6)

式(6)中:μ為材料的泊松比。

考慮材料和外荷載的隨機性，式(5)中的D、T、Π、χ、d都為隨機量，按照二階泰勒級數展開為

(7)

(8)

(9)

(10)

(11)

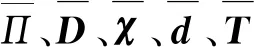
把式(7)～式(11)代入式(5)中，可得總勢能泛函Π的二階展式為

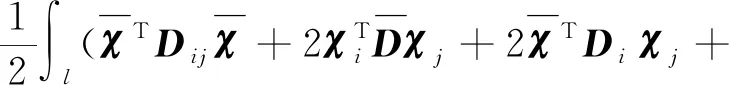
(12)

基于攝動隨機變分原理[3]，直接得到總勢能泛函二階展開式的一階變分，并考慮式(13)、式(14)。

(13)

(14)

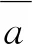
可得

(15)

(16)

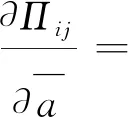
(17)

完成式 (15)～式(17)的整理分析的基礎上，得到控制方程為

(18)

(19)

(20)

(21)

(22)

(23)

2 結構可靠指標及其梯度優化迭代算法

2.1 結構可靠指標

把對箱梁結構有影響的基本隨機變量X作為自變量時，可得描述極限狀態的功能函數Z為

Z=g(X)

(24)

結構的可靠指標為

(25)

2.2 結構可靠指標的求解

(26)

式(26)中：G為功能函數；min表示取最小值。

采用迭代公式[式(26)][5]計算驗算點x(k+1)，其計算公式為

(27)

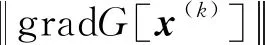
3 基于攝動隨機有限元法的可靠指標求解

3.1 功能函數

用局部平均法[14]離散箱型梁隨機場，得到隨機變量X，其功能函數為

g(X)=u*-u(X)

(28)

式(28)中：u*對應于控制截面的最大容許撓度；u(X)為對應于箱梁正常使用極限狀態的撓度響應。

3.2 功能函數的梯度

2.2節利用式(27)迭代尋找驗算點的關鍵是確定梯度向量gradG(x)。一般這種情況下，原變量空間中的功能函數g(X)可以得到，求梯度向量gradG(x)可轉化為求gradg(X)，可表示為

(29)

式(29)中：函數g(X)不能用隨機變量顯式表示，可表示為

g(X)=g(R,S)

(30)

式(30)中：R和S分別為結構抗力和作用效應。

則有

gradg(X)=JRgR+JSgS

(31)

式(31)中，gR、gS分別為函數g(X)對R和S的梯度向量；JR、JS分別為R、S的雅克比矩陣。

由式(31)可以看出，求出雅克比矩陣JR、JS及梯度向量gR、gS是關鍵問題。一般情況下，JR、gR和gS容易獲得。由于結構的隨機效應S不易用X顯式表達，所以難以用解析法求解雅克比矩陣JS。

3.3 攝動隨機有限元法求梯度向量

如3.1節所述，可以選取一個結點的位移a作為箱梁極限狀態方程中控制截面的響應量。求解1節中控制方程，可以求得ai。雅克比矩陣JS第i行的轉置是響應S的一階偏導數，有

Si=ai，i=1,2,…,n

(32)

ai可根據式(18)、式(19)求得

(33)

即而可以確定JS為

JS=[ai]T,i=1,2,…,n

(34)

進而由式(31)求出梯度向量gradg(X)。

3.4 正態相關隨機變量的處理

如果得到了相關正態隨機變量X，需要把X轉化為標準正態隨機變量x。

首先，通過正交變換得到不相關的正態隨機變量Y，可表示為

Y=ATX

=[Y1,Y2,…,Yn]T

(35)

式(35)中：A為與隨機變量協方差矩陣CX的特征值λi(i=1,2,…,n)相應的n個正交規范化特征向量形成的矩陣。

然后，標準化Y，得到不相關的標準正態隨機變量xi為

(36)

式(36)用矩陣表示為

(37)

式(37)中：T為特征值矩陣。

結合式(36)可得

(38)

將3.3節推導得到的gradg(X)和式(38)代入式(29)就可以得到標準正態隨機變量空間中功能函數的梯度gradG(x)。然后，由式(27)可以用優化迭代算法得到驗算點坐標，即而得到可靠指標。

3.5 簡化迭代分析

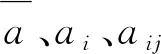
(39)

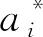
(40)

4 算例分析

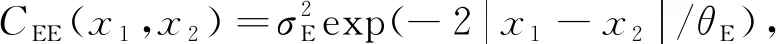
(41)

當箱型梁兩端為固定端，分別取兩種工況考慮箱梁的隨機性，利用基于驗算點的攝動隨機有限元可靠度算法(計算結果標記為PSFEM1)及其簡化迭代計算方法(計算結果標記為PSFEM2)計算在不同變異系數情況下箱型梁的可靠指標。以蒙特卡洛有限元法(計算結果標記為MCS)可靠度計算結果為基準，分析PSFEM1和PSFEM2的誤差。

從圖3可以看出，在不同變異系數下，PSFEM1和PSFEM2的計算結果比較相近，兩者之間誤差在工況一和工況二情況下分別不超過1.83%和0.48%，與文獻[15]結論較為一致。可以看出，當變異系數增大時，兩種方法的計算誤差都增大。變異系數不超過0.15時，PSFEM1在兩種工況下與MCS的誤差分別小于4.66%和4.09%，PSFEM2在兩種工況下與MCS的誤差分別小于6.28%和4.52%。對比之下，在不同變異系數下，在工況一情況下較多采用PSFEM1，在工況二情況下可以用PSFEM2代替PSFEM1。

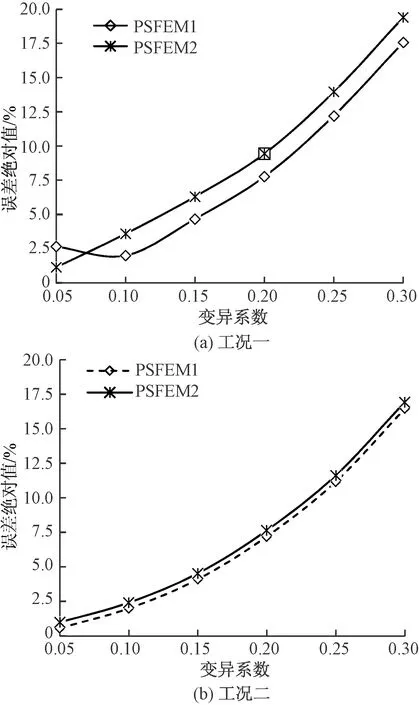
圖3 不同工況下比較PSFEM1和PSFEM2的計算結果

將工況一情況下PSFEM1和MCS的計算結果進行比較，比較結果如圖4所示。

從圖4可以看出，隨著變異系數的增大，兩種方法計算的結構可靠指標都減小，從而說明隨著隨機參數變異系數的增大，箱梁的可靠度降低。當隨機參數變異系數小于0.15時，PSFEM1和MCS的計算結果非常相近。當隨機參數變異系數大于0.15時，兩者的計算結果逐漸偏離，變異系數為0.20、0.25和0.30時的偏離誤差分別為7.75%、12.20%和17.57%。以上說明只有隨機參數小變異時，PSFEM1具有較好的計算精度。

圖4 工況一下比較PSFEM1和MCS的計算結果

在工況一下，采用基于驗算點的可靠度算法(記為PSFEM-1)；在工況二下，采用簡化迭代算法(記為PSFEM-2)。計算箱梁中點的可靠指標及其與隨機場變異系數的關系，并將計算結果進行對比，對比結果如圖5所示。

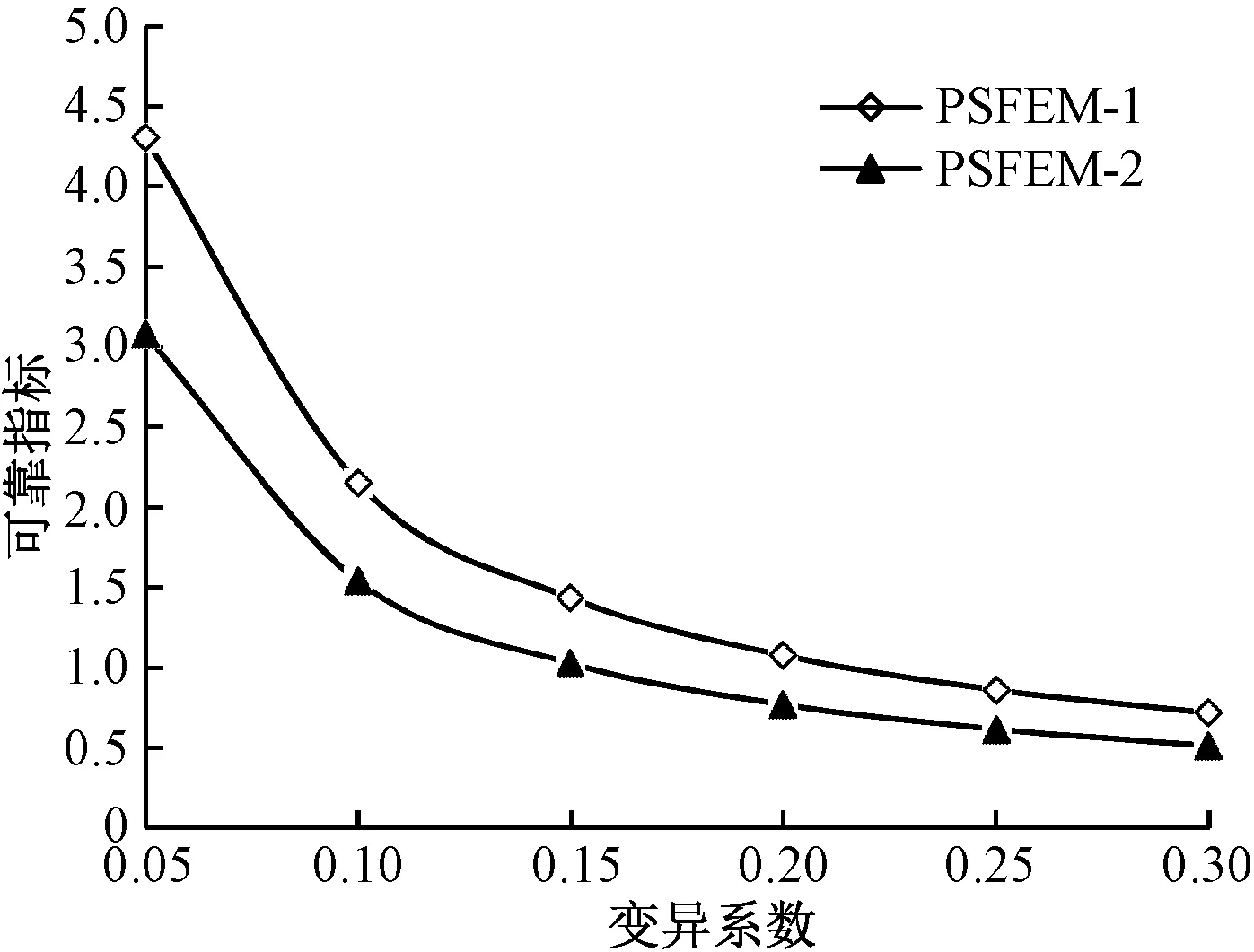
圖5 比較PSFEM-1和PSFEM-2的計算結果

從圖5可以看出，隨著隨機參數變異系數的增大，兩種不同工況下計算的可靠指標都逐漸減小，說明隨機參數的變異性對箱梁結構的可靠度是不可忽視的影響因素。在同一變異系數下，PSFEM-1的計算的結果大于PSFEM-2的計算結果，說明在彈性模量具有隨機性的基礎上，荷載具有隨機性時，箱型梁的可靠度也會相應降低。

5 結論

基于箱梁附加撓度建立了箱梁可靠度分析的攝動隨機有限元法，研究對比了基于驗算點和簡化迭代算法，得出如下結論。

(1)在彈性模量隨機和彈性模量荷載隨機兩種工況下，基于驗算點的迭代算法結果與其簡化迭代算法的結果比較接近，誤差分別小于1.83%和0.48%。

(2)在彈性模量隨機情況下，在隨機參數小于0.15時，基于驗算點的迭代算法結果具有良好的計算精度，與基于蒙特卡洛有限元算法的結果誤差不超過4.66%，其簡化迭代算法計算結果誤差是6.28%；在彈性模量荷載隨機情況下，在隨機參數小于0.15時，基于驗算點的迭代算法及其簡化迭代算法的結果都具有良好的計算精度，與基于蒙特卡洛有限元算法的結果誤差不超過4.09%和4.52%。

(3)基本變量的隨機性對箱型梁的可靠度有明顯影響，參數變異性越大，可靠指標下降越大；在彈性模量具有隨機性的基礎上，荷載具有隨機性時，箱型梁的可靠度也會相應降低。因此，分析和設計箱梁結構時，結構參數隨機性的影響不容忽視。